小车路径规划

本项目全部代码已同步上传至Github,仓库链接：Asgard-Tim/Path-Planning: 重庆大学明月科创实验班定量工程设计方法课程项目 (github.com)

一、设计要求

---

在本部分的课程项目中，要求我们运用LD14雷达扫描地图，在MATLAB中进行人工势场添加并对STM32小车进行路径规划，在一规定的场地中让小车避开两个矩形障碍物并以尽可能短的路径最终抵达圆形目标位置。

二、系统方案

---

2.1 移动底盘分析

小车为履带式小车，左右履带分别由一枚直流电机进行驱动，运动模式类似常规双轮小车，通过左右两枚电机转动的差速实现转向。该小车相对来说较为容易进行控制，只需要控制两个驱动轮的速度存在差异，即两轮差速，即可控制机器人实现无滑动摩擦的旋转，也可实现零半径转弯。

图2-1 双轮履带小车外观图

图2-2 两轮差速式机器人运动学分析图

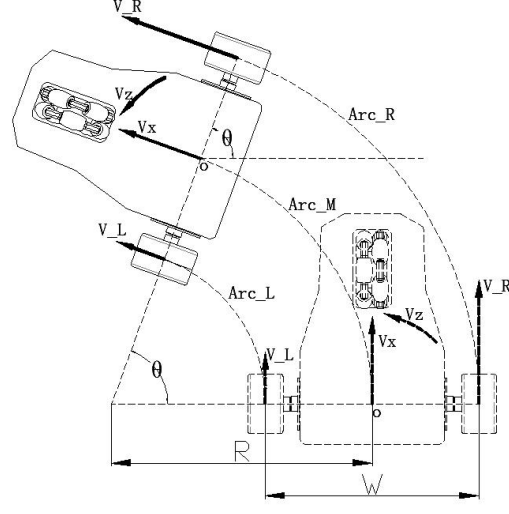
对小车移动底盘的运动学分析（如上图2-2所示）：

小车的速度控制主要是控制 X 轴（前后方向）和 Z 轴（旋转方向）的速度， 以 Vx 和 Vz 来指代，单位分别是 m/s 和弧度/s。X 轴方向以前进记为正，Z 轴方向以右转记为正。车轮速度是使用编码器来计算和得出，读取编码器计数后再转化成车轮的速度。Vz则是通过左右电机转动的差速计算得到的。

图中参数分别代表：

2.2 电机特性分析

在本次项目中，我们采用带有减速器与编码器的直流电机驱动小车前进。

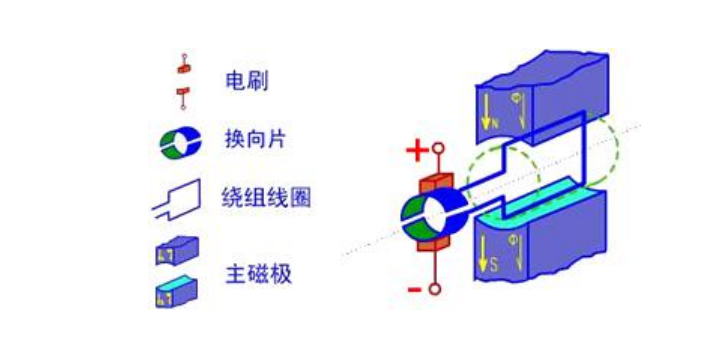
直流电机的物理模型图如下图2-3所示。其中，固定部分有磁铁，这里称作主磁极；固定部分还有电刷。转动部分有环形铁心和绕在环形铁心上的绕组。 (其中 2 个小圆圈是为了方便表示该位置上的导体电势或电流的方向而设置的) 它的固定部分（定子）上，装设了一对直流励磁的静止的主磁极 N 和S，在旋转部分（转子）上装设电枢铁心。在电枢铁心上放置了两根导体连成的电枢线圈， 线圈的首端和末端分别连到两个圆弧形的铜片上，此铜片称为换向片。换向片之间 互相绝缘，由换向片构成的整体称为换向器。换向器固定在转轴上，换向片与转轴 之间亦互相绝缘。在换向片上放置着一对固定不动的电刷 B1 和 B2，当电枢旋转时，电枢线圈通过换向片和电刷与外电路接通。在电刷上施加直流电压 U,电枢线圈中的电流流向为：N 极下的有效边中的电流总是一个方向，而 S 极下的有效边中的电流总是另一个方向。这样两个有效边所受的洛伦兹力的方向一致（可以根据左手法则判定），电枢开始转动。具体来说就是，把上图中的+和-分别接到电池的正极和负极，电机即可转动；如果是把上图中的+和-分别接到电池的负极和正极，则电机会反方向转动。电机的转速可以理解为和外接的电压是正相关的（实际是由电枢电流决定）。

总而言之，如果我们可以调节施加在电机上面的直流电压大小，即可实现直流 电机调速，改变施加电机上面直流电压的极性，即可实现电机换向。

图2-3 直流电机的物理模型

在具体的使用过程中，我们需要通过在特定的引脚之间（如本次项目所用电机为1/6引脚）接上一个直流电源，电机即可转动，且改变电压大小即可改变电机转速。接线方式说明如下图2-4所示。

2.3 电机控制策略以及PID特性分析

小车电机驱动器芯片使用 AT8236，具有过流保护功能，并可设置电流阈值。驱动芯片只需两个逻辑输入，便可达到调速和正反转的功能，本小车中，每个电机使用两路PWM进行调速（实际上一个普通 IO 和一路 PWM 即可进行正反转 和调速）。

电机的速度使用 13 线霍尔编码器输出 AB 相进行测量，电机减速比为 1:30，使用 STM32 的编码器测量功能，并初始化为脉冲上升沿和下降沿都进行计数，可实现轮子转一圈输出 1560 个计数。

电机调速框图如下图2-5所示。

图2-5 电机调速框图

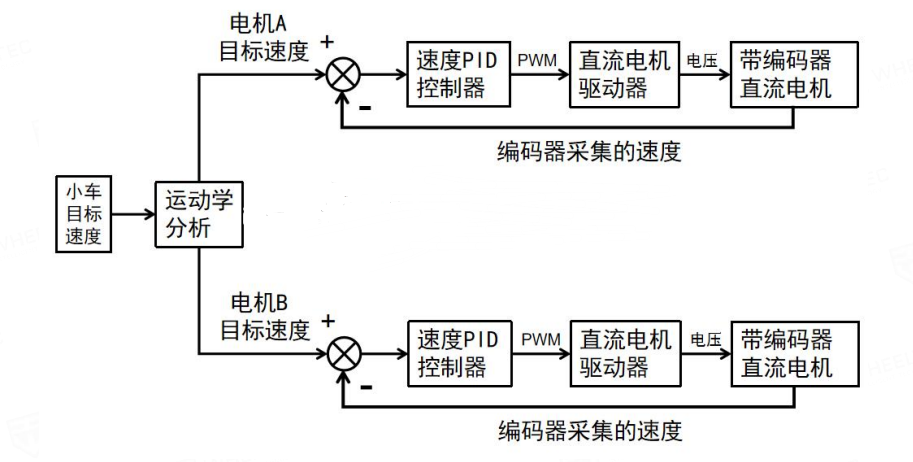
基于2.1节提到的小车移动地盘的运动学分析，我们可以进一步讨论这些物理量之间的关系，并求出其运动学正逆解公式（如下图2-6），结合PID实现控制。

图2-6 两轮差速式机器人的运动学正逆解公式

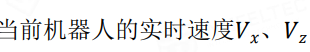
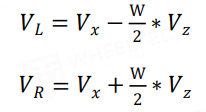
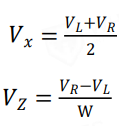
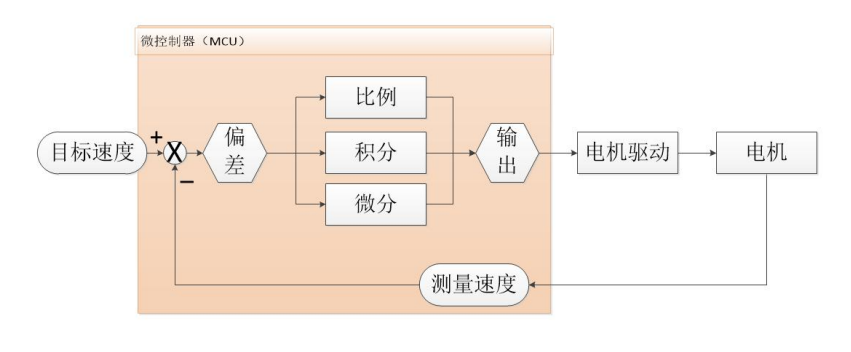
下图2-7为PID的控制框图，每个方块代表控制系统的一个组成部分，从图中可看出系统中各组成部分的相互关系和影响，即 PID 调节系统是具有被调参数负反馈的闭环系统。当被控量 Y 受到干扰的影响而升高时，反馈信号将高于给定值 X，经过比较而到放大元件去的偏差信号 e 将为负值，控制器将发出信号而使执行元件动作，其作用方向为负，使被控量下降，这就达到了自动控制的目的。

图2-7中的目标速度一般我们可以通过按键或者开关等方式编程实现改变目标值，测量速度就是通过单片机定时去采集编码器的数据并清零。目标速度和测量速度之间做差这个就是目前系统的偏差。在控制过程中，需要将目标速度、测量速度与偏差三者送入 PID 控制器进行计算输出，然后再经过电机驱动的功率放大控制电机的转动去减小偏差，最终达到目标速度。

图2-7 PID控制框图

对于上述PID控制的基于C语言的实现，我们给出以下代码：

`int Incremental_PI (int Encoder,int Target)` 

`{` 

`static float Bias,Pwm,Last_bias;` 

`Bias=Encoder-Target; //计算偏差` 

`Pwm+=Velocity_KP*(Bias-Last_bias)+Velocity_KI*Bias;`

 `//增量式 PI 控制器` 

`Last_bias=Bias; //保存上一次偏差` 

`return Pwm; //增量输出` 

`}`

其中，入口参数为编码器的速度测量值和速度控制的目标值，返回值为电机控制 PWM。第一行是相关内部变量的定义。第二行是求出速度偏差，由测量值减去目标值。第三行使用增量 PI 控制器求出电机 PWM。第四行保存上一次偏差，便于下次调用。最后一行是返回。

2.4 嵌入式控制系统总结分析

总体而言，我们基于小车本身的轮距等基本参数编写了一整套嵌入式PID控制流程与系统（基于C语言，面向STM32编程），结合PWM波控制电压，从而控制电机的转速以实现对于车轮速度的反馈调节机制，能够保证小车始终保持相对稳定的速度前进，便于后面进一步规划算法，使小车的运动更加可控。此部分编写的KEIL工程详见附件“PID.zip”。

2.5 传感系统总结分析

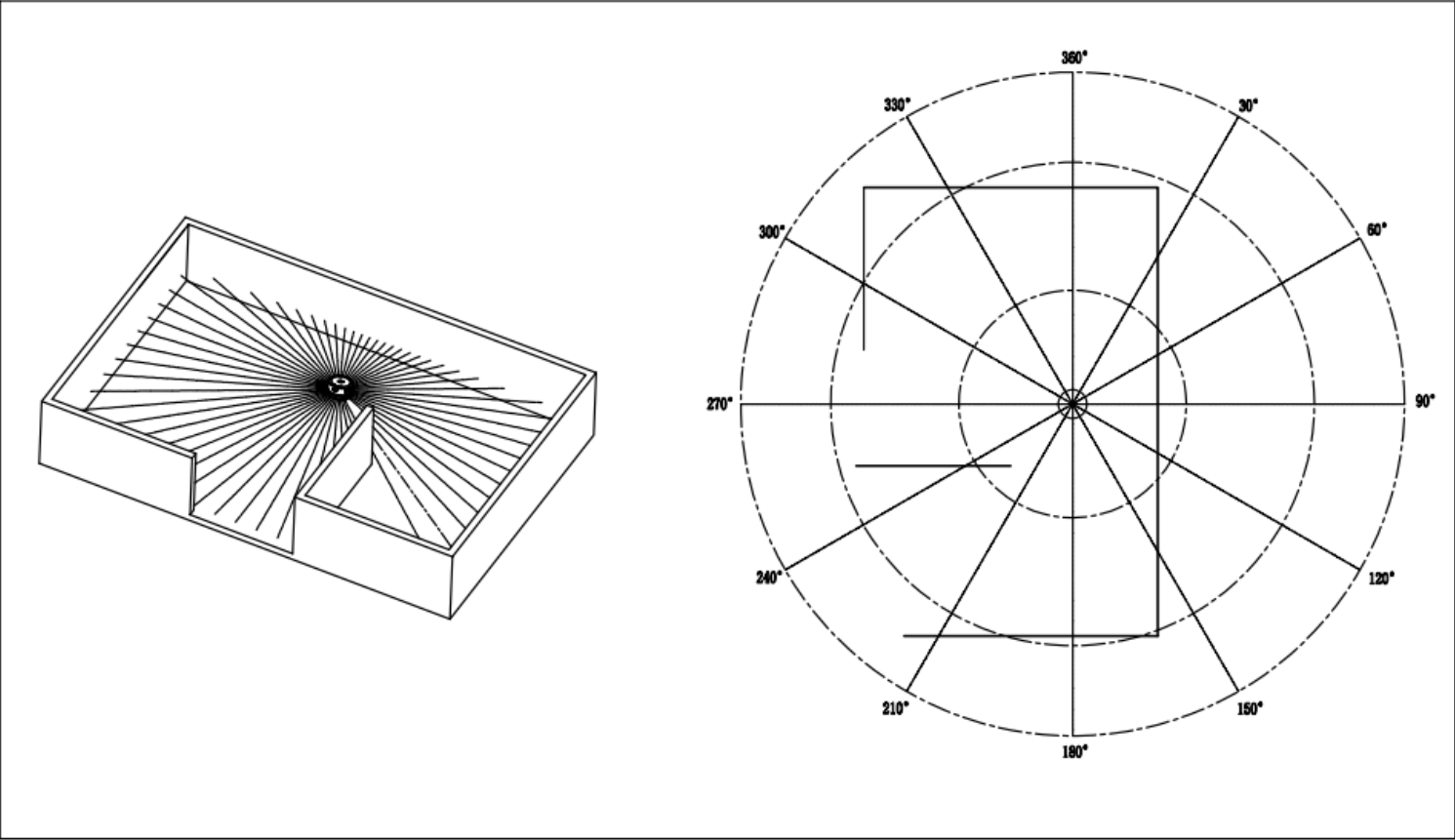
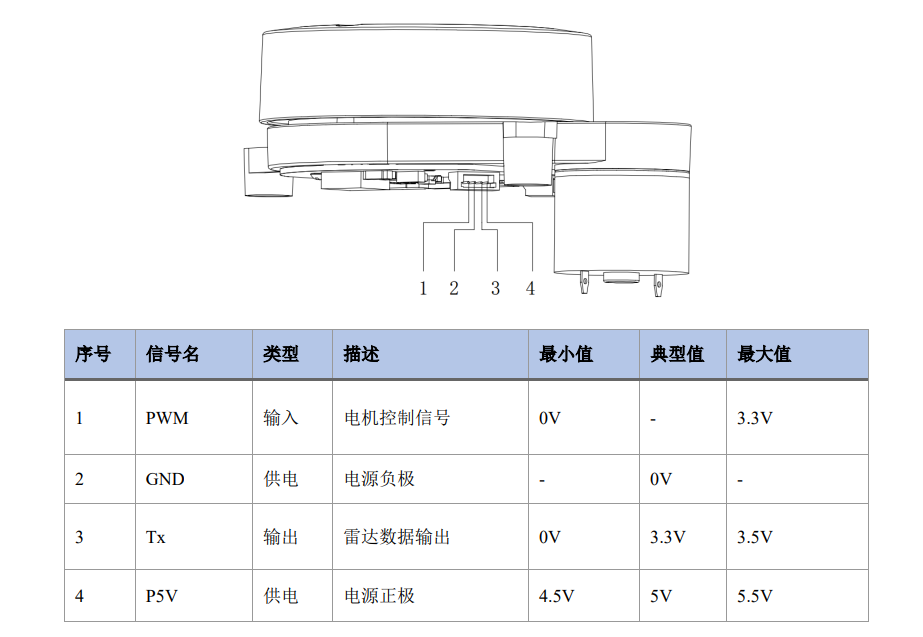
本次项目所采用的传感器主要为激光雷达，在此我们选用LD14雷达。LD14 主要由激光测距核心，无线传电单元，无线通讯单元，角度测量单元、电机驱动单元和机械外壳组成。LD14测距核心采用三角测量法技术，可进行每秒 2300 次的测距。每次测距时，LD14从一个固定的角度发射出红外激光，激光遇到目标物体后被反射到接收单元。通过激光、目标物体、接收单元形成的三角关系，从而解算出距离。获取到距离数据后，LD14 会融合角度测量单元测量到的角度值组成点云数据，再进行导出。

雷达扫描点云数据形式如下图2-8所示：

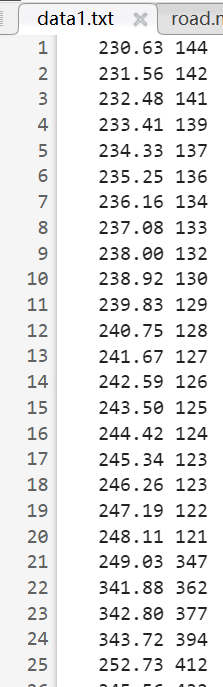
图2-8 雷达扫描点云极坐标数据形式（下图2数据为角度（角度制），右侧为距离）

在项目的实践过程中，我们需要通过对STM32单片机进行编程，从激光雷达读取数据并通过串口将处理后的数据传输至电脑中（用特定的软件读取串口输出信息）。STM32中烧录的KEIL工程见附件“Lidar.zip”，接线方式如下图所示。

图2-9 激光雷达与单片机接线方式对应

这里给出KEIL工程中main.c中的主干代码（图2-10），最终会输出数据θ和r,分别代表偏转的角度（AvoidData[i].angle）和距离原点的距离（AvoidData[i].distance）。

图2-10 读取激光雷达数据的主干代码

三、硬件电路设计

---

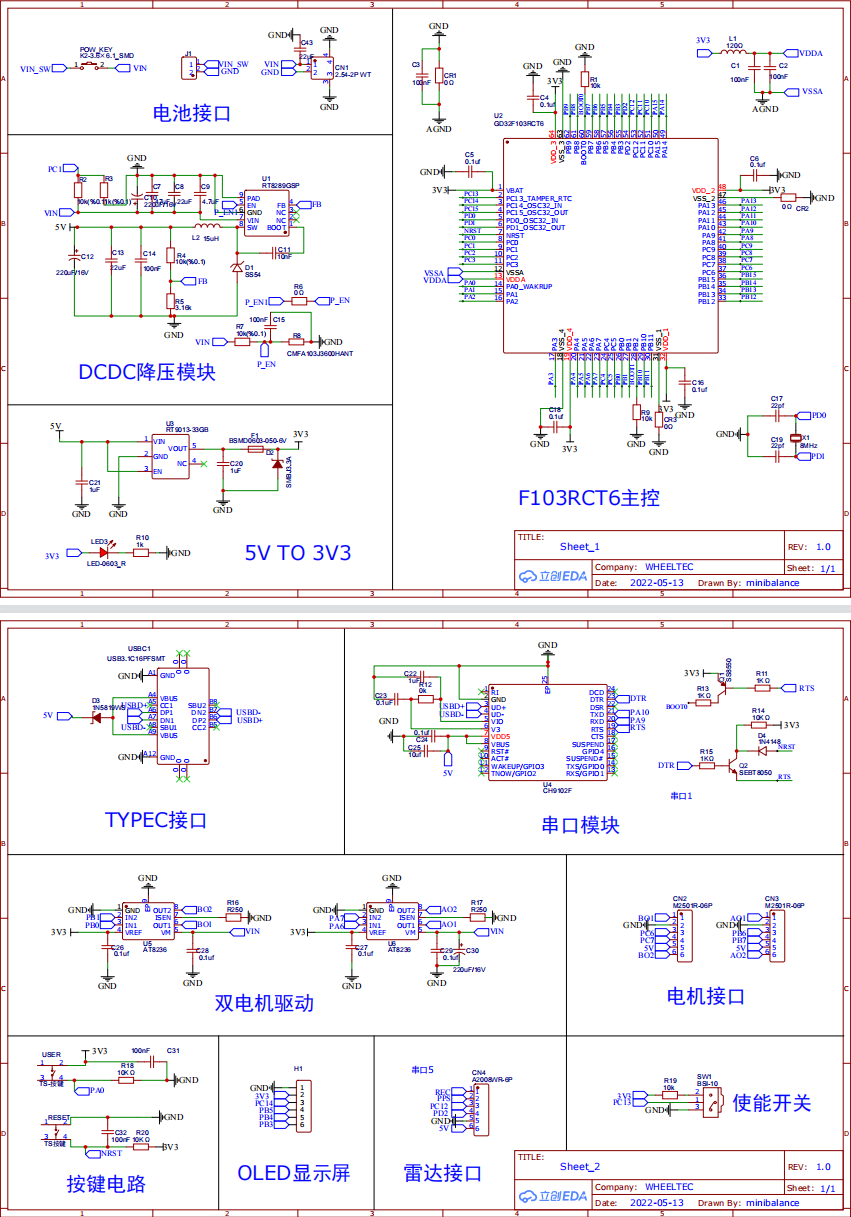
主要运用模块电路图如下图3-1所示：

图3-1 主要模块电路图

其中，小车的主控为STM32 F103RCT6芯片，其主控板实物图如下图3-2所示：

图3-2 STM32主控板实物图

由于本次项目需要完成的目标较为单一，仅使用其中少部分接口和器件。

四、软件算法设计

---

4.1 任务描述

在本项目中，我们需要通过激光雷达对于小车所处的地图环境（2m*2m，放置有三个正方体障碍物与一个圆柱体目标物）进行扫描，并对扫描得到的数据结果进行处理。通过一定的算法对于目标物与障碍物进行识别后，我们还需要通过人工势场法进行路径规划，使得小车能够以最优的路径绕开障碍物到达目标物。

本次项目任务分为静态和动态两个部分，其中动态测试过程中会对障碍物的位置进行人为的随机改动。测试过程中，小车的起点位置与目标物的位置始终不变，且可自由选定小车的初始面对方向。

4.2 技术路径和策略

通过对于任务描述的分析，我们大致可以将静态情况下的路径规划问题拆解为以下几个部分，并给出相应的处理工具与解决策略：

• （1） 地图扫描：需要通过对STM32单片机进行编程（利用软件工具KEIL），利用串口通信读取激光雷达扫描所获取的周围地图环境点云的极坐标数据
• （2） 处理数据：将串口所得到的数据导入MATLAB中，利用坐标变换将不同点位扫描的极坐标数据统一到同一个笛卡尔坐标系中以便后续处理与识别
• （3） 识别物体：在获取扫描后得到的地图后，需要利用RANSAC算法（随机抽样一致算法）识别点云数据中的直线与圆形，并得到相应的障碍物与目标物的二维坐标
• （4） 路径规划：在MATLAB中编程，利用得到的出发点、障碍物和目标点各自的坐标建立势场，并用梯度下降法寻找避开障碍物、到达目标点的最优路径

实际上，在动态情况下的路径规划问题中，实现的步骤也与上述大致相同，只是并没有MABLAB等电脑端的辅助软件帮助其进行数据处理与路径规划，需要将这些算法通过对STM32单片机编程集成到小车上，从而实现在测试地图环境随机发生改变的情况下仍然能够按照局部最优的路线避开障碍物到达目标点。

4.3 核心程序逻辑

4.3.1 激光雷达极坐标点云数据的处理与变换——得到二维地图

在2.5节，我们给出了我们的KEIL工程。通过将其烧入至STM32内，并按照特定接线方式将激光雷达与主控板连接，利用串口通信及相关软件成功在电脑上读取了激光雷达扫描得到的点云极坐标数据（如图2-8右图）。在实际测试时，我们选取了五个坐标点分别放置小车（控制朝向相同）对周围地图环境进行扫描，获得了“data1.txt”等一系列数据文件（详见附件）。

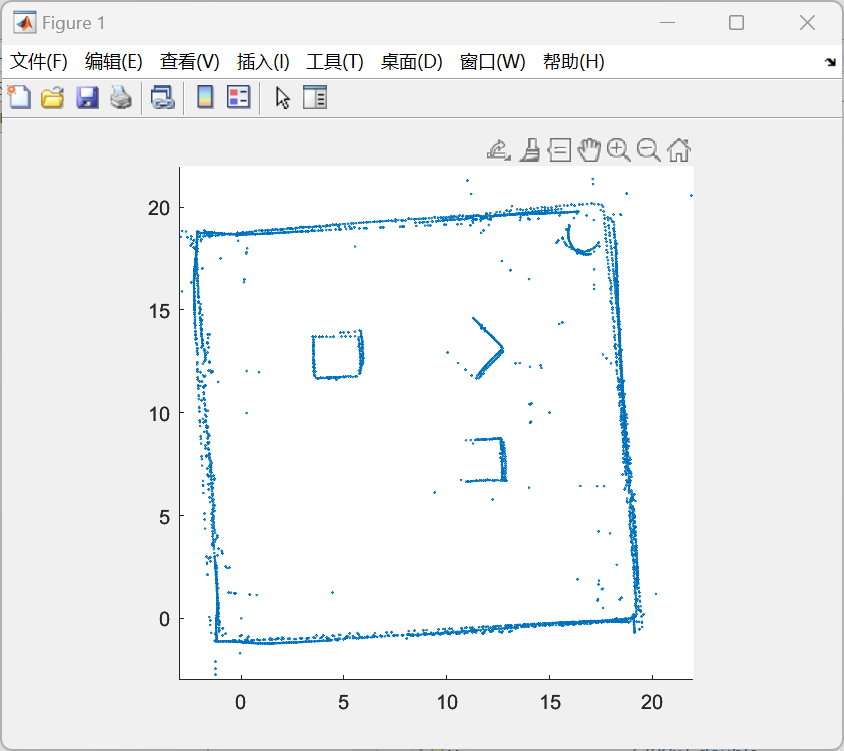
在MATLAB程序的第一部分，我们首先利用importdata函数从数据文本文件中读取相应数据，并将其按列分割为“angle”和“distance”两部分。随后，我们利用MATLAB中自带的坐标变换函数pol2cart将一系列的极坐标数据转换为笛卡尔坐标系下的x-y数据（算法原理如下图4-1）。事实上，由于小车每次扫描的位置均不同，因此还需要将多次扫描的结果结合每次小车放置位置的坐标进行一系列的拼接与变换，才可得到最终的场地二维地图（效果如下图4-2）。

图4-1 利用pol2cart函数进行坐标变换的原理示意图

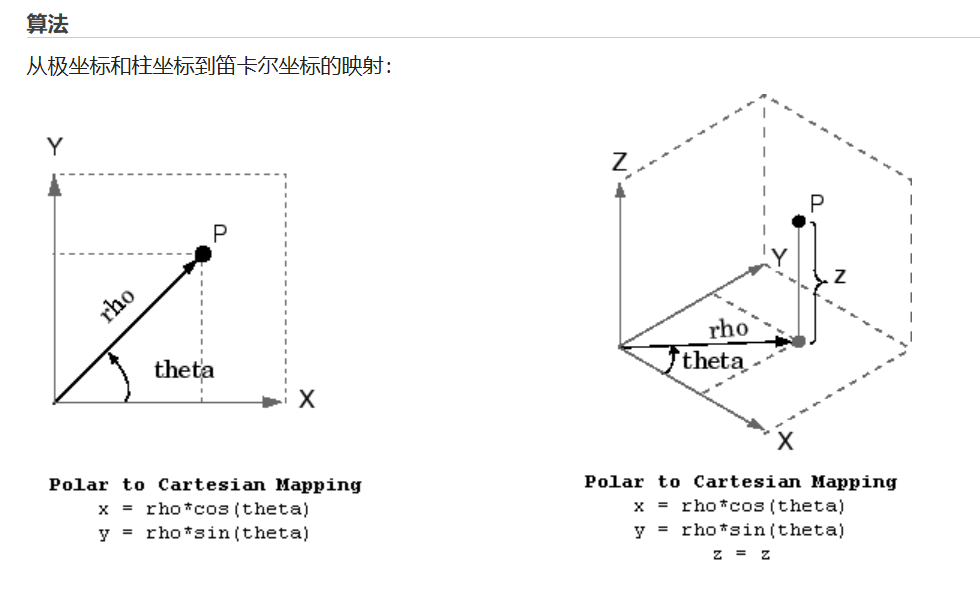
图4-2 经拼接后得到的场地二维地图

该部分的代码给出如下：

`%Step1:处理激光雷达扫描数据，绘制二维坐标系地图`

`ans=importdata("data1.txt");`

`angle=ans(:,1);`

`angle=angle.*2.*3.1415926./360;`

`distance=ans(:,2);`

`[x,y] = pol2cart(angle,distance);`

`ans1=importdata("data2.txt");`

`angle1=ans1(:,1);`

`angle1=angle1.*2.*3.1415926./360;`

`distance1=ans1(:,2);`

`[x1,y1] = pol2cart(angle1,distance1);`

`ans2=importdata("data3.txt");`

`angle2=ans2(:,1);`

`angle2=angle2.*2.*3.1415926./360;`

`distance2=ans2(:,2);`

`[x2,y2] = pol2cart(angle2,distance2);`

`ans3=importdata("data4.txt");`

`angle3=ans3(:,1);`

`angle3=angle3.*2.*3.1415926./360;`

`distance3=ans3(:,2);`

`[x3,y3] = pol2cart(angle3,distance3);`

`ans5=importdata("data5.txt");`

`angle5=ans5(:,1);`

`angle5=angle5.*2.*3.1415926./360;`

`distance5=ans5(:,2);`

`[x5,y5] = pol2cart(angle5,distance5);`

`x4 = [x;x1-100;x2+1850;x3+1400;x5+1500]/100;`

`y4 = [y;y1+1750;y2+100;y3+1650;y5+1000]/100;`

`figure(1);`

`scatter(x4,y4,1);`

`hold on`

`axis equal`

`axis( [ -3, 22, -3, 22 ] )`

4.3.2 利用RANSAC算法识别地图中的直线和圆——获得目标点与障碍物的坐标

在成功利用激光雷达的扫描数据建立了二维地图后，我们需要让机器人知道哪里能走哪里不能走，要走向哪里，即明确目标点以及障碍物的具体坐标。在本测试项目中，设定圆柱为目标物而正方体为障碍物，所以问题的关键即为如何从二维地图中识别出圆形以及正方形（本质上为直线的拼接）并获得其坐标。

在之前的课程中，介绍了RANSAC这一算法。随机样本一致性(Random Sample Consensus RANSAC) 是一种迭代方法，用于从包含异常值的观察数据中估计出数学模型参数，因此也可以理解为一种异常值检测方法。RANSAC的一个基本假设是，数据由内点(“inliers”)和外点(“outliers”)组成，其中内点是在一定误差范围内可以通过一些模型参数来解释的数据，外点是不符合模型的数据。RANSAC的另一个假设是，随机选取的样本数据都是内点，存在一个可以估计模型参数的过程，该模型可以最佳地解释或拟合该数据。通过该算法，我们可以有效地从已有的地图（本质上是二维坐标系下的点集数据）中拟合出直线与圆的轮廓，并获取相应图形的对应坐标。

该算法的实现步骤如下：

（1） 从原始数据集S中随机选择子集s，s为假设的内点(子集s一般为最小子集，如：直线选取两个点，圆选择三个点)

（2） 依据子集s估计模型参数

（3） 遍历数据集S中除子集s外的所有数据，如果数据点在给定误差e以内，则标记为内点，否则标记为外点

（4）所有内点组成一致集，如果一致集中点的个数满足给定阈值T，则用一致集中所有内点重新估计模型参数，然后结束算法

（5）如果一致集中内点个数少于阈值T，则重新选择新的子集s，并重复步骤（1）-（4）

（6） 经过K次迭代，选择一个内点数量最多的一致集，用一致集中所有内点重新估计模型参数，然后结束算法

基于上述基本思想与步骤，我们编写了一段MATLAB代码，用于二维坐标地图中直线的识别与拟合。在此基础之上，我们根据算法原理，从点集中随机取出三个点，利用三点成圆获得圆的方程（利用自己编写的函数ThreePoint2Circle）。再对圆的轨迹赋予一个宽度，统计落入这个宽度中的点的数量，对所有的点进行逐个取点，获得最优的圆的方程。值得注意的是，由于待识别的正方形是由多条直边构成，这要求我们需要重复对于该图像进行扫描拟合，且需要在一次拟合之后将该次拟合中涉及的数据点删除以防影响下次拟合。下面将给出这一部分的代码实现以及拟合效果（如图4-3、4-4）。

`%Step2:利用RANSAC算法识别直线和圆`

`%(1)圆的识别`

`a = [x4,y4];`

`% RANSCA参数：`

`% 迭代次数`

`iter = 0;`

`% 查看圆数据的大小`

`[m,n] = size(a);`

`% 误差参数`

`berr = 0.02;`

`% 拟合参数`

`bfit = [];`

`% 内点个数为点数的1/3`

`t = floor(m/3);`

`% 开始循环迭代`

`while iter<100`

  `% 随机挑选三个点，三个点不重复`

  `% 拟合圆最少需要三个点，拟合直线最少需要两个`

  `% ran为索引编号`

  `ran = randperm(m,3)';`

  `% b为索引得到的点`

  `b = a(ran,:);`

  `% 根据随机得到的三个点，计算圆的半径和圆心`

  `[r1,p1] = ThreePoint2Circle(b(1,1:2), b(2,1:2), b(3,1:2));`

  `% 选择除了随机得到的三个点外的其他点`

  `c = setdiff(a,b,"rows");`

  `% 计算每个点到圆心的距离dis`

  `dis = sqrt(sum((c(:,1:2)-p1).^2,2));`

  `% 计算 dis和拟合圆的误差`

  `res = dis - r1;`

  `% 选择小于误差的点，进入到内点中`

  `d = c(res<berr,:);`

  `len = length(d(:,1));`

  `% 判断内点数量是否满足条件`

  `if len > t`

​    `% 满足条件时，多点拟合圆，这里用平均值计算圆心`

​    `p = mean(d);`

​    `r = mean(sqrt(sum((d(:,1:2)-p(:,1:2)).^2,2)));`

​    `% 多点拟合的圆和随机点拟合的圆的误差`

​    `err = sqrt(sum((p-p1).^2))+sqrt((r-r1)^2);`

​    `% 如果误差满足条件，则可以结束循环`

​    `% 不满足则继续`

​    `if err < berr`

​      `bfit = [p,r];`

​      `berr = err;`

​      `break`

​    `else`

​      `iter = iter+1;`

​       `continue`

​    `end`

  `else`

​    `iter = iter+1;`

  `end`

`end`

`%绘图`

`para = [p(1)-r, p(2)-r, 2*r, 2*r];`

`rectangle('Position', para, 'Curvature', [1 1]);` 

`%（2）直线的识别`

`iter = 100;`

`data1=transpose(x4);`

`data2=transpose(y4);`

`data=[data1;data2];`

`for t=1:10`

 `number = size(data,2); % 总点数`

 `bestParameter1=0; bestParameter2=0; % 最佳匹配的参数`

 `sigma = 1;`

 `pretotal=0;   %符合拟合模型的数据的个数`

 `for i=1:iter`

 `%随机选择两个点`

   `idx = randperm(number,2);` 

   `sample = data(:,idx);` 

   `%拟合直线方程 y=kx+b`

   `line = zeros(1,3);`

   `x = sample(:, 1);`

   `y = sample(:, 2);`

   `k=(y(1)-y(2))/(x(1)-x(2));   %直线斜率`

   `b = y(1) - k*x(1);`

   `line = [k -1 b];`

   `mask=abs(line*[data; ones(1,size(data,2))]);  %求每个数据到拟合直线的距离`

   `total=sum(mask<sigma);       %计算数据距离直线小于一定阈值的数据的个数`

   `if total>pretotal      %找到符合拟合直线数据最多的拟合直线`

​     `pretotal=total;`

​     `bestline=line;     %找到最好的拟合直线`

  `end` 

 `end`

`%显示符合最佳拟合的数据`

 `mask=abs(bestline*[data; ones(1,size(data,2))])<sigma;`  

 `hold on;`

 `k=1;`

 `index=[];`

 `for i=1:length(mask)`

  `if mask(i)`

​    `inliers(1,k) = data(1,i);`

​    `k=k+1;`

​    `index=[index i];`

  `end`

 `end`

 `%删除完成拟合的点以进行下一次拟合`

 `for i=1:length(index)`

  `data(:,index(i))=[];`

  `for j=1:length(index)`

​    `if(index(j)>index(i))`

​      `index(j)=index(j)-1;`

​    `end`

  `end`

 `end`

 `% 绘制最佳匹配曲线`

 `bestParameter1 = -bestline(1)/bestline(2);`

 `bestParameter2 = -bestline(3)/bestline(2);`

 `xAxis = min(inliers(1,:)):max(inliers(1,:));`

 `yAxis = bestParameter1*xAxis + bestParameter2;`

 `plot(xAxis,yAxis,'r-','LineWidth',2);`

`end`

`function [R,P0] = ThreePoint2Circle(P1, P2, P3)`

`%% 求圆心和半径，三个点可以求圆心和半径`

  `x1 = P1(1);  x2 = P2(1);  x3 = P3(1);`

  `y1 = P1(2);  y2 = P2(2);  y3 = P3(2);`

  `z1 = x2^2 + y2^2 - x1^2 - y1^2;`

  `z2 = x3^2 + y3^2 - x1^2 - y1^2;`

  `z3 = x3^2 + y3^2 - x2^2 - y2^2;`

  `A = [(x2-x1), (y2-y1); (x3-x1), (y3-y1); (x3-x2), (y3-y2)];`

  `B = 0.5*[z1; z2; z3];`

  `P0 = (A'*A)\A'*B;`

  `R1 = sqrt( (P0(1) - P1(1))^2 + (P0(2) - P1(2))^2 );`

  `R2 = sqrt( (P0(1) - P2(1))^2 + (P0(2) - P2(2))^2 );`

  `R3 = sqrt( (P0(1) - P3(1))^2 + (P0(2) - P3(2))^2 );`

  `R = (R1 + R2 + R3)/3;`

  `P0 = P0';`

`End`

图4-3（上） 对于二维地图中一条直线的拟合（红线为拟合结果）

（可以看到拟合效果相对良好）

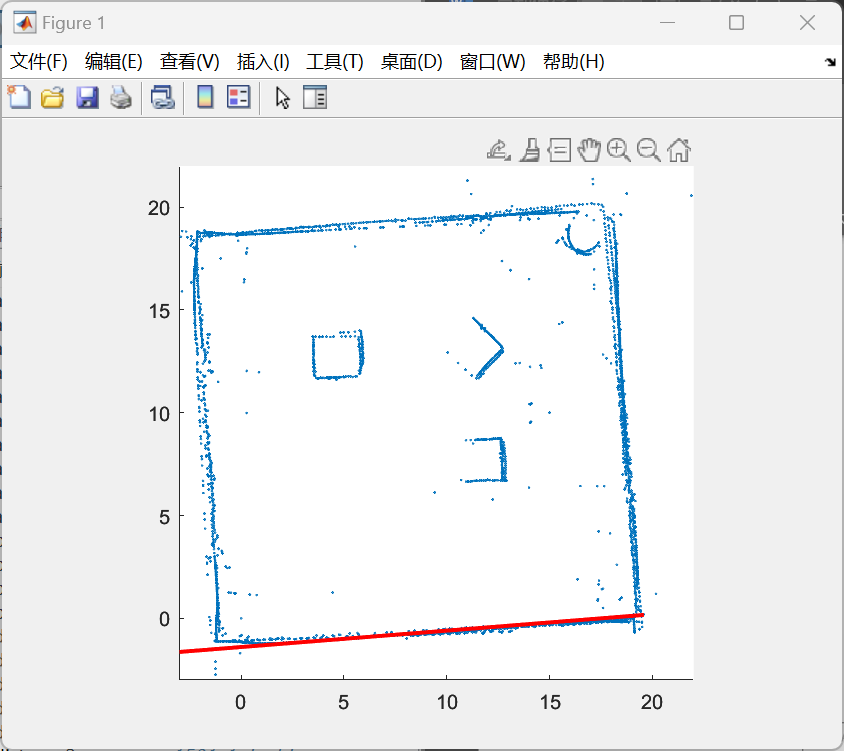
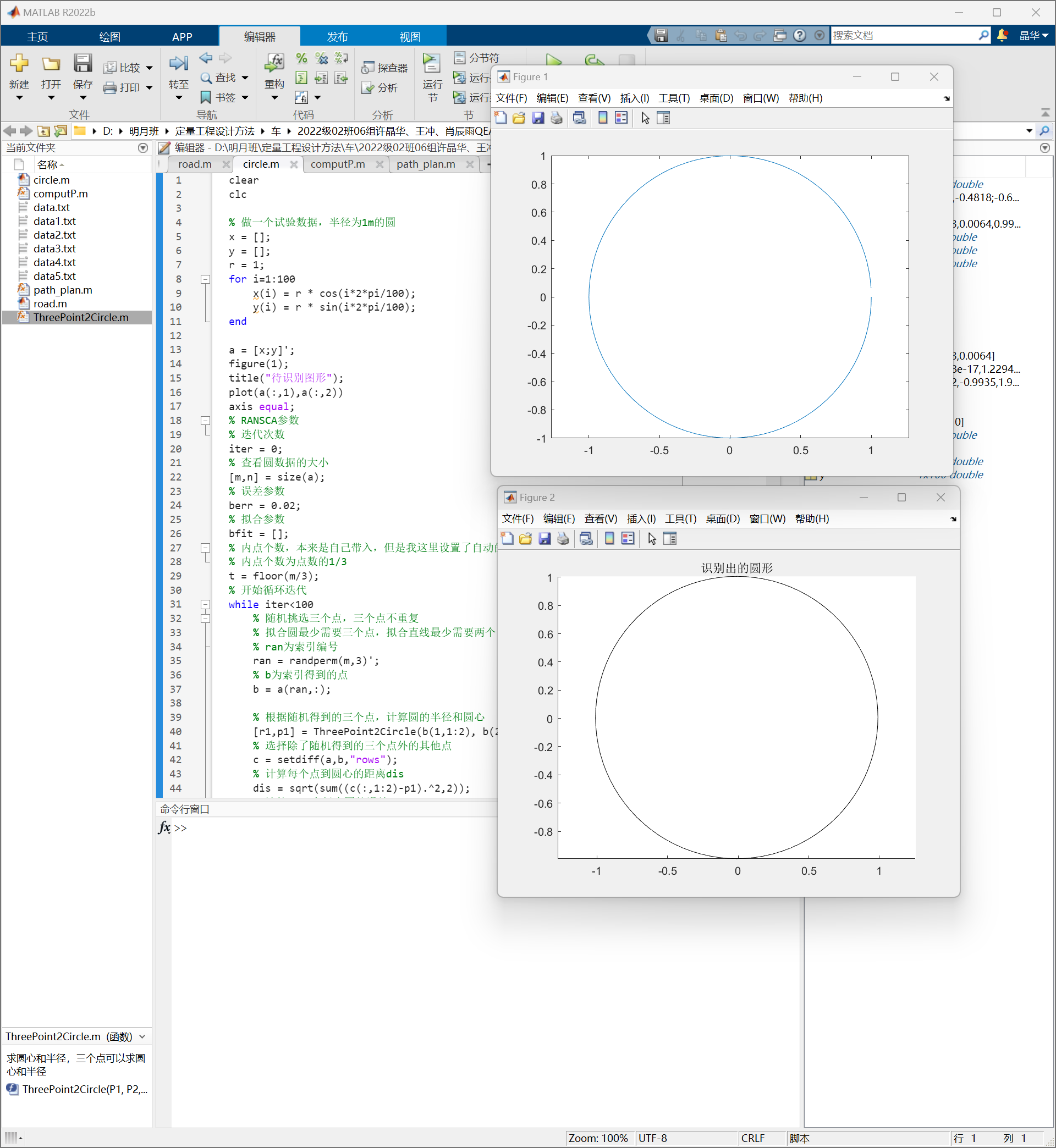
图4-4（右） 对于给定圆坐标数据的RANSAC拟合（上图为给定的圆，下图为拟合出的圆）

（说明该算法实现的有效性）

4.3.3 建立势场并利用梯度下降法确定最优路径（人工势场法）

人工势场法引入了物理中斥力场和引力场的思想，把工作环境抽象为一个电磁场，而机器人则是其中的一个电荷，机器人在磁场力的作用下移动。人工势场法会在障碍物周围构建斥力场、在目标点周围构建引力场；这样，机器人便能够在斥力场和引力场的作用下向目标点移动。同时，当障碍物和目标点太近时，机器人很可能会因为刹不住车而出现无法到达目标点等问题，这也就出现了一堆相应的优化算法。

通过利用RANSAC算法对于地图中具有特定形状的边界、障碍物与目标物进行识别，我们成功获得了障碍物与目标点的坐标。在此基础之上，我们基于原型函数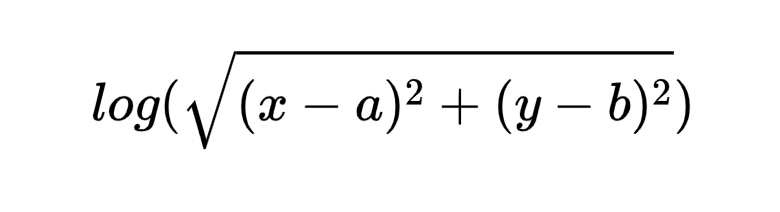（a,b即为障碍物/目标点的x,y坐标）建立势场。通过观察不难发现，在以（a,b）为圆心、半径为1的圆之外的地方该势函数均为正，反之为负。事实上，对于场地内的3个障碍物以及1个目标物而言，所形成的是一个叠加场，由原型函数作用于不同的点叠加而成。在此，我们不妨认为势场为正处具有排斥力而势场为负处具有吸引力，需要吸引小车向目标点走去而花费尽量少的能量。在这样的算法理念基础上，我们需要在代表目标点的原型函数部分加上负号；更进一步的，我们还希望这个吸引力足够大而防止被障碍物阻断，因此在建立势场时，不妨在代表目标点的原型函数前乘上一定的系数以保证其足够强大的吸引力。最终，我们根据地图实际情况，建立了整个势场叠加后的函数方程：F=log(sqrt((x-4.75).^2+(y-12.5).^2))+log(sqrt((x-12).^2+(y-7.6).^2))+log(sqrt((x-11.2).^2+(y-13).^2))-5*log(sqrt((x-16.5).^2+(y-18.5).^2))，并根据该函数绘制了势能图（如图4-5）与等势线图（如图4-6)。

图4-5 势场函数势能图

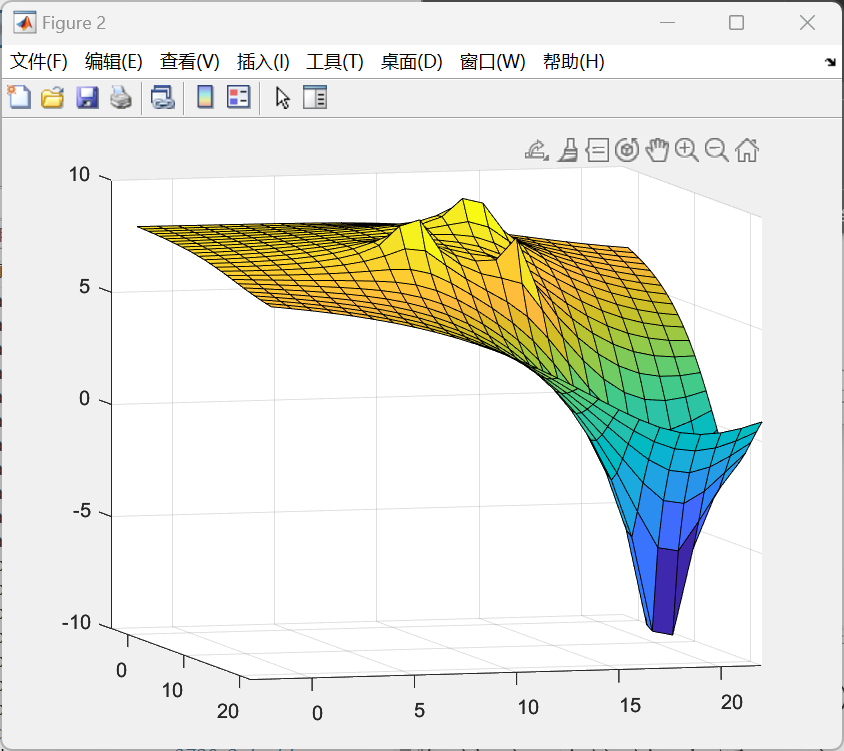
图4-6 势场函数等势线图

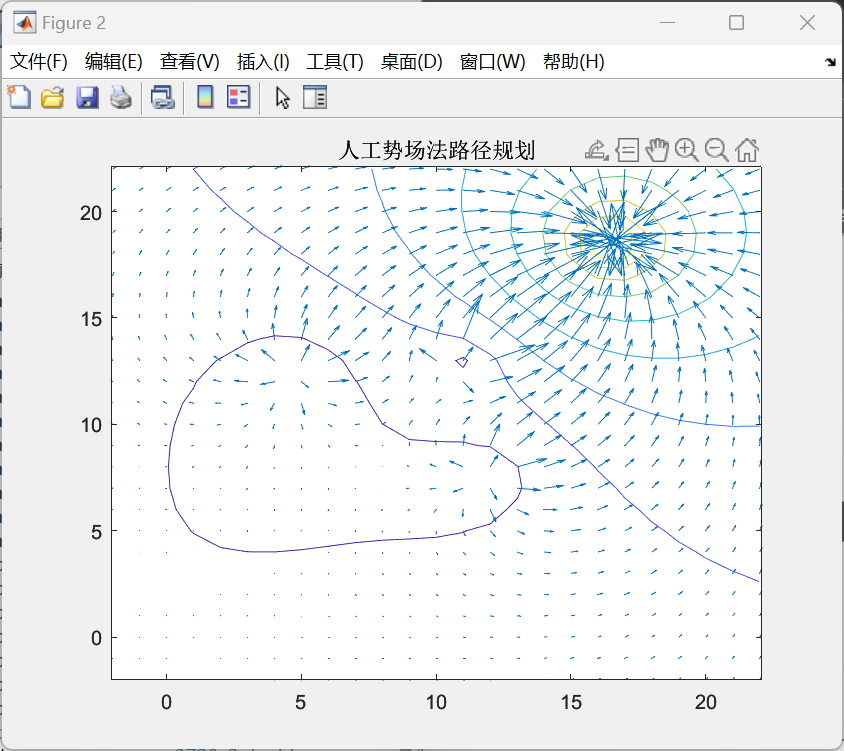
该部分代码如下：

`%Step3:通过识别得到的障碍物和目标坐标建立势场`

`v=-2:1:22;`

`[x,y]=meshgrid(v);`

`F=log(sqrt((x-4.75).^2+(y-12.5).^2))+log(sqrt((x-12).^2+(y-7.6).^2))+log(sqrt((x-11.2).^2+(y-13).^2))-5*log(sqrt((x-16.5).^2+(y-18.5).^2));`

`[px,py]=gradient(F,1,1);`

`contour(x,y,F);`

`hold on;`

`title('人工势场法路径规划');`

`quiver(x,y,px,py,0);`

`figure(2);`

`surf(x,y,-F);`

在建立完势场之后，由于我们需要寻找的是避开障碍物而通往目标点的最优路径，实际上即为所耗费能量最少的路径，我们引入了梯度下降法，通过间隔相同距离的不断迭代，在每一处都寻找能量下降最快的方向（即为梯度方向）前进（在MATLAB中通过调用函数文件path_plan.m与computP.m实现该功能），最终得到了如下图4-7绿色线所示的最优路径。

图4-7 人工势场法路径规划结果（绿色即为规划出的最优路径）

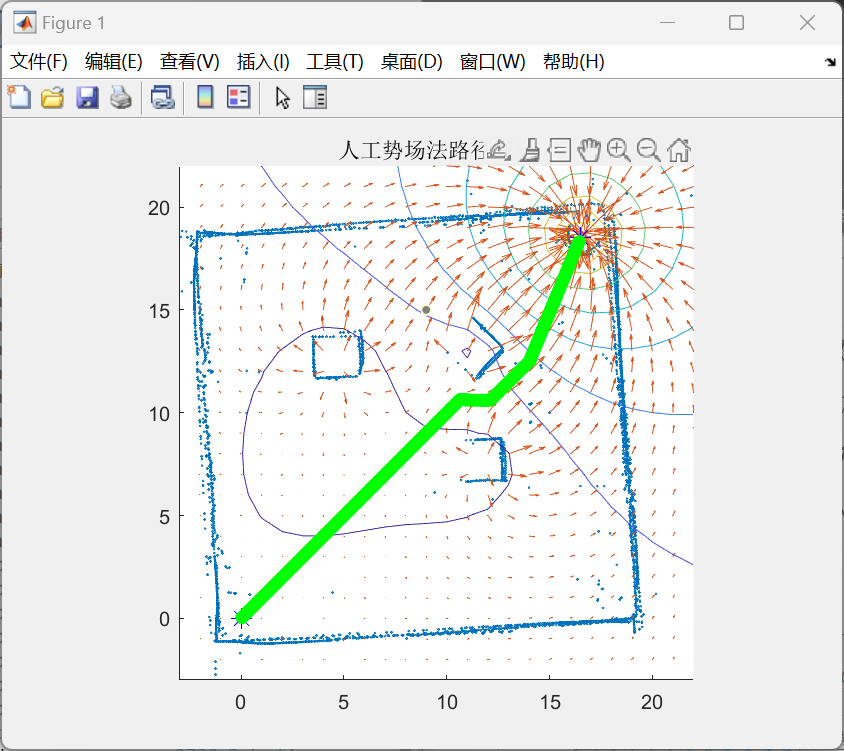
其中，path_plan函数是整个算法过程中的关键，也是梯度下降思想的集中体现，其大致实现思路流程如下：

1）起点、终点 、障碍物、迭代次数、取点半径等参数的设定

2）以起点为中心，作半径为r的圆，从圆上取八个均布的点

3）分别计算八个点的前进“代价”—— 终点对其的引力+所有障碍物对其的斥力

4）取“代价”最小的点的坐标，结合现有起点，计算得到新的起点，然后重复上述内容

5）当发现 一个点距离终点很近 or 迭代的次数计算完 程序停止。

该部分的实现代码如下：

`%Step4:通过人工势场法确定最优路径`

`axis([-3 22 -3 22]);`

`begin=[0;0]%起始点坐标`

`over=[16.5;18.5];%目标点坐标`

`figure(1);`

`hold on;`

`plot(begin(1),begin(2),'*b','MarkerSize',10);`

`plot(over(1),over(2),'*b','MarkerSize',10);`

`obstacle=[4.75,12,11.35;12.75,7.5,12];%障碍物坐标`

`point= path_plan(begin,over,obstacle);`

`function [ point ] = path_plan(begin,over,obstacle)`

`iters=1; %迭代次数`

`curr=begin;`

`testR=0.1;  %测试8点的圆的半径为0.1`

`while (norm(curr-over)>0.2) && (iters<=2000)`

  `point(:,iters)=curr;`

`%   attr=attractive(curr,over);`

`%   repu=repulsion(curr,obstacle);`

`%curoutput=computP(curr,over,obstacle);`

  `%计算当前点附近半径为0.2的8个点的势能，然后让当前点的势能减去8个点的势能取差值最大的，确定这个方向，就是下一步迭代的点`

  `%先求这八个点的坐标`

  `for i=1:8    testPoint(:,i)=[testR*sin((i-1)*pi/4)+curr(1);testR*cos((i-1)*pi/4)+curr(2)];`

​    `testOut(:,i)=computP(testPoint(:,i),over,obstacle);`

​    `%找出来最小的就可以了`

  `end`

  `[temp num]=min(testOut);`

  `%迭代的距离为0.1`

  `curr=(curr+testPoint(:,num))/2;`

  `plot(curr(1),curr(2),'og');`

  `iters=iters+1;`

`end`

`end`

`function [ output ] = computP( curr,over,obstacle )`

 `k_att=1;`

`repu=0;`

`k_rep=100;`

`Q_star=2;`

`%计算当前点距离终点的引力`

`attr=1/2*k_att*(norm(curr-over))^2;`

`%计算障碍点与当前点的斥力`

`%设定障碍的斥力作用半径为2`

`for i=1:size(obstacle,2)`

   `if norm(curr-obstacle(:,i))<=Q_star`

​    `repu=repu+1/2*k_rep*(1/norm(curr-obstacle(:,i))-1/Q_star)^2;`

  `else`

​    `repu=repu+0;`

  `end`

`end`

`output=attr+repu;`

`end`

4.4 实现的实际效果

事实上，尽管RANSAC算法在理论上已经具备足够的拟合精度，但在实际的识别过程中，由于激光雷达扫描获取的数据过多而导致干扰噪点的数量达到了一定规模，以及在算法参数设置上考虑到算力有限等因素而没有采用精确度最高的设置，诸如此类的干扰因素导致在多条直线识别时出现了互相覆盖与识别错误的情况，识别圆形时也并未识别出目标点的圆柱所在处，因此在实际的测试过程中，利用RANSAC算法识别圆与直线以获取目标点和障碍物坐标这一过程并未取得特别良好的效果。为了后面的路径规划算法顺利开展，我们最终采用人工识别的方式，分别给出了起点、障碍物以及目标点的大致坐标，并顺利实现了利用人工势场法进行路径规划的算法，合理规划出了从起点避开障碍物到达目标点停下的最优路径，并通过STM32单片机编程成功驱动了小车按照规划好的路径进行运动，顺利完成开环测试。

五、实验结果及分析

---

经过几次测试，在进行4至5个位置的扫描之后，通过将数据进行变换与拼接，可以得到一张较为完整的二维地图，再将地图中通过RANSAC算法识别出的特定点位数据读入程序运行，可以得到一条较为合理的最优路径。

事实上，在前面的嵌入式控制系统设计部分，我们计划采用PID方式对于小车与电机进行反馈调节控制，但在实际的测试中，PID的控制方式实现的效果并不尽如人意，无法合理利用MATLAB路径规划所得到的数据结果顺利完成测试。于是我们果断选择了重新使用PWM的方式，依托于MATLAB程序运行规划出的路径对应的相关数据计算所需要的PWM以及延时的时间。最终采用的代码如下图5-1所示（具体KEIL工程内容详见Run.zip附件)。

图5-1 PWM电机驱动部分实现代码

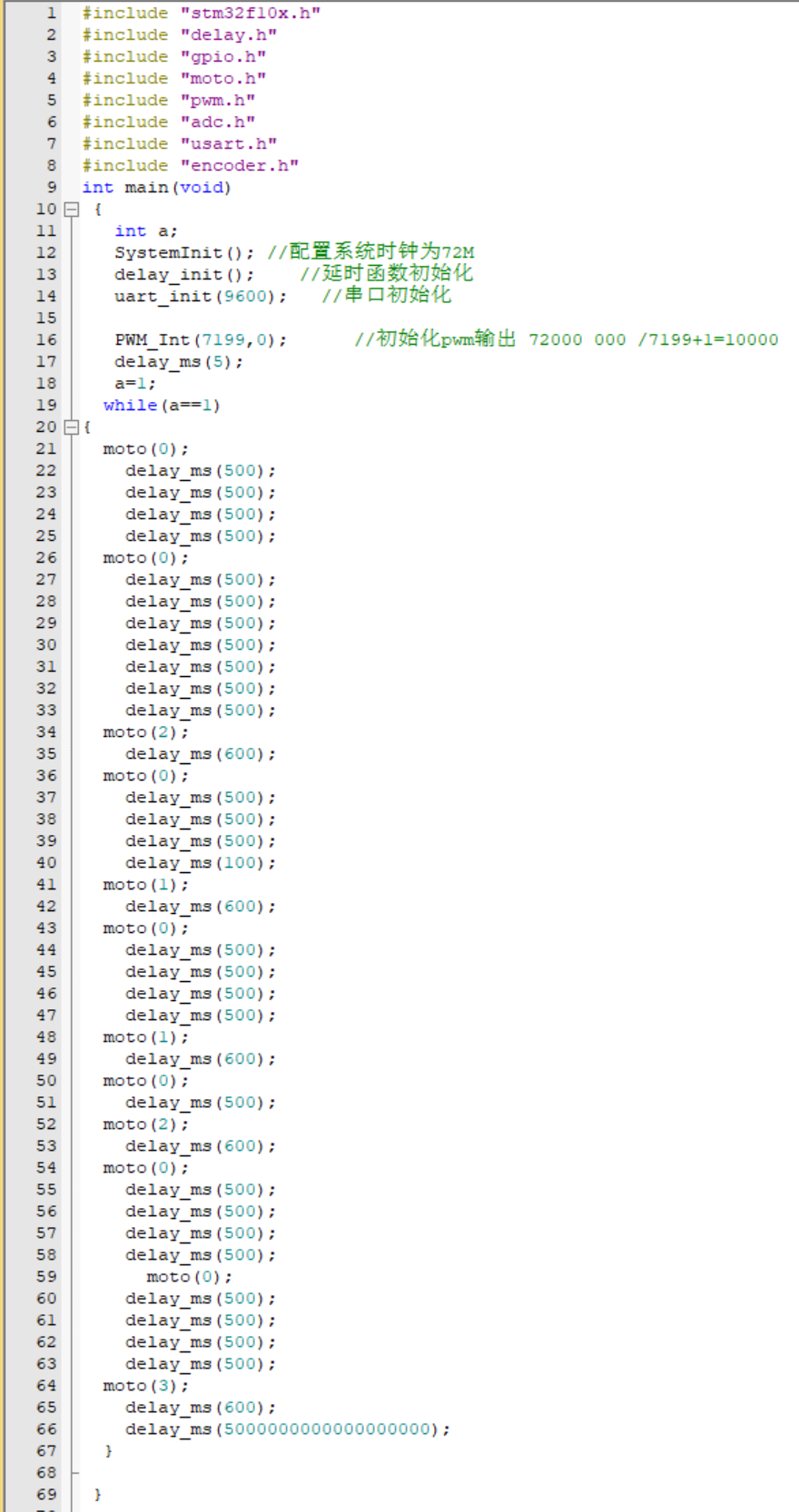
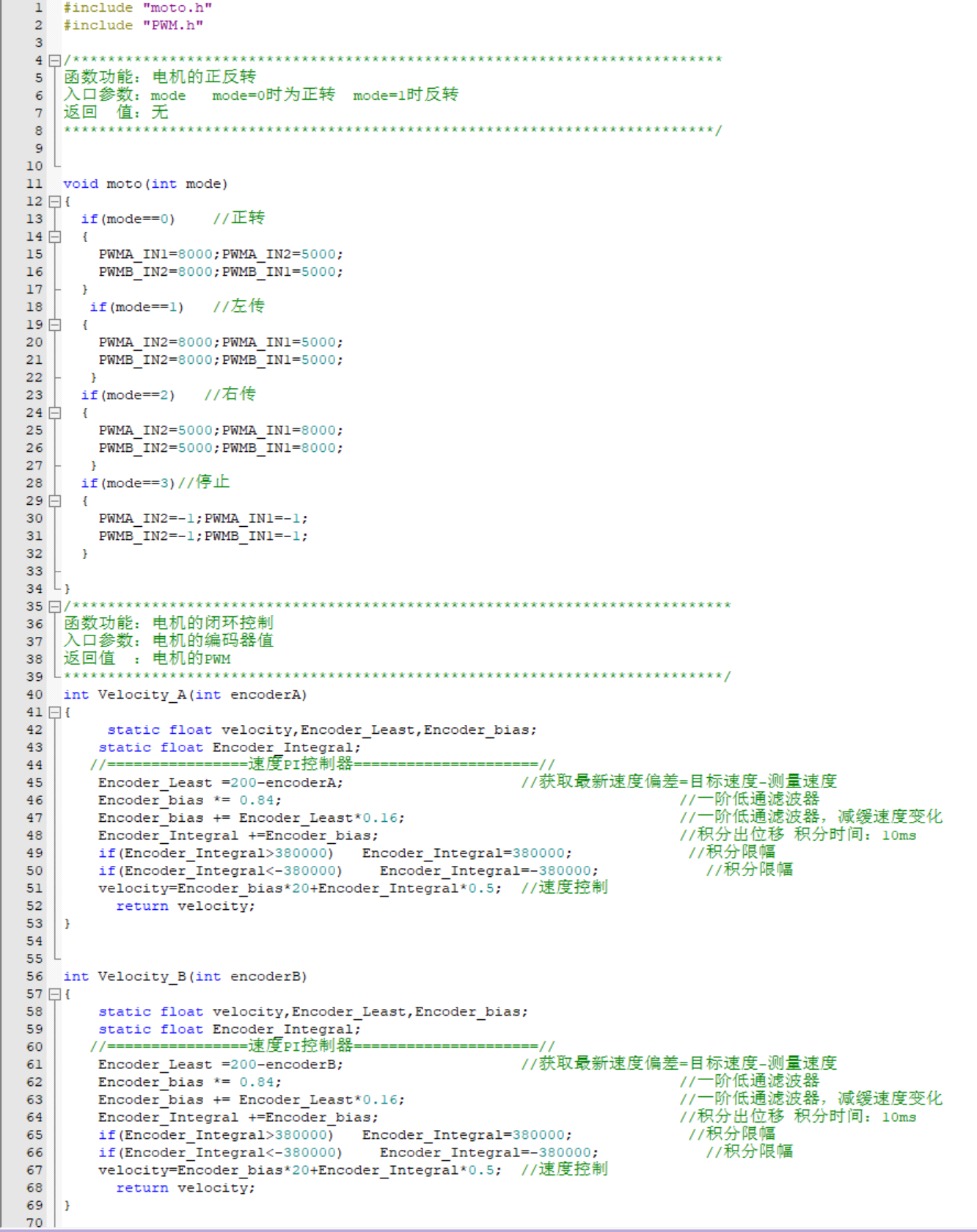
通过调整PWM的方式对小车进行开环运动控制，最终可以较好达到项目要求。（实现效果见下图5-2及视频附件“测试.mp4”）

图5-2 静态路径规划实现效果实地测试

虽然静态路径规划部分完成情况相对较好，但遗憾的是，由于对于C语言编程不是特别熟悉，包括受限于对库的了解、算法的时间复杂度较高、实现繁琐以及对于STM32内部利用效率的不完全开发等因素，最终并没有能够成功完成动态部分的路径规划。事实上，动态情况下的路径规划更符合我们在日常生活中常见的应用场景，不论是扫地机器人还是汽车导航，本身所应对的环境都在时刻发生着改变，因此动态的路径规划问题仍然值得在课程结束之后继续进行深挖和探索。希望在未来的工程实践中，我们能够以更加定量化的思维去分析和思考问题，同时更加熟练的掌握相关的算法设计，提高自己的硬件嵌入式编程能力。

六、个人总结

---

在路径规划这一阶段的课程中，我在前半段主要负责的是STM32单片机的一些基础开发，对于其基本的开发流程以及GPIO等基本的功能模块有了一定的了解并能进行一些简单的32单片机编程；在后半段，我主要负责整体路径规划项目的思路整理与算法设计，结合课堂上介绍的RANSAC识别算法以及人工势场法规划路径，课下积极结合概念的巩固以及相关资料的查询，阅读了相关的示例代码，并根据算法的整体思路自己动手实现了RANSAC算法对于直线与圆的识别拟合以及在建立的势场中利用梯度下降法实现路径规划的MATLAB程序，积极将自己的算法实现与队友编写的STM32 C语言程序融合在一起，在与队友的充分交流沟通与合作的基础上共同完成了该项目。在死亡之桥的测试项目中，我在一个人调试了单片机程序许久未果后，与队友进行了积极的沟通与合作，也基本确定了由我负责编写MATLAB算法程序给队友的单片机编程提供数据支持的合作模式，对于我们团队的所有人来说都是一次难忘的经历。在利用激光雷达扫描地图的过程中，我们也充分信任彼此，在他们编写好了读取雷达数据的相关程序后，我结合着MATLAB程序的需求对于KEIL代码的输出格式部分进行了一定的修改，在通力合作下最终圆满完成了该项任务。除此之外，也非常感谢整个课程阶段过程中凌睿老师在算法思路方面对我们进行的一系列教学与指导以及助教学长们在答疑时的倾力相助。