课题:斯特林发动机热力循环计算及分析
根据选定的斯特林发动机类型,确定具体的传动机构,开展斯特林发动机的热力循环计算;从最大化斯特林发动机单次循环的输出功角度出发,优化斯特林发动机系统所涉及的传动机构、相位角等参数。
一、背景介绍
通过学习本课程,我们需要完成斯特林发动机的设计与制造过程,在此过程中掌握工程设计全流程中的基本技能。之所以选择斯特林发动机,是因为能够将热能转化为机械能,并具有以下特点:
- 效率高:斯特林发动机的热效率相对较高,与理论上最高热效率的卡诺循环相同,实际中可以达到30%以上,远高于传统内燃机;
- 噪音低:斯特林发动机工作过程中没有爆炸过程,工作过程相对平滑,噪音和振动较小;
- 热源多:斯特林发动机作为一种外燃机,可以直接利用任何可用热源,如太阳能、地热能与生物质能等可再生能源;
- 排放少:斯特林发动机在工作过程中没有直接燃烧,为闭口系统,工质环境友好,没有任何有害物排放;
- 寿命长:连续运行,安全可靠,对高温侧材料要求较高。
斯特林发动机的概念可以追溯到19世纪初,但由于技术限制和市场竞争,长期以来并没有像内燃机那样广泛应用。最近,随着对环保和能源效率的关注不断增加,斯特林发动机再次引起了一些研究兴趣,在水下动力、太阳能动力、空间站动力、热泵空调动力,车用混合推进动力等方面得到了广泛的研究与重视,并且已得到了一些成功的应用。
斯特林发动机按照结构可分为α型、β型和γ型三类,其中α型又称为双动力活塞式发动机,β型和γ型又称为配气活塞式发动机。
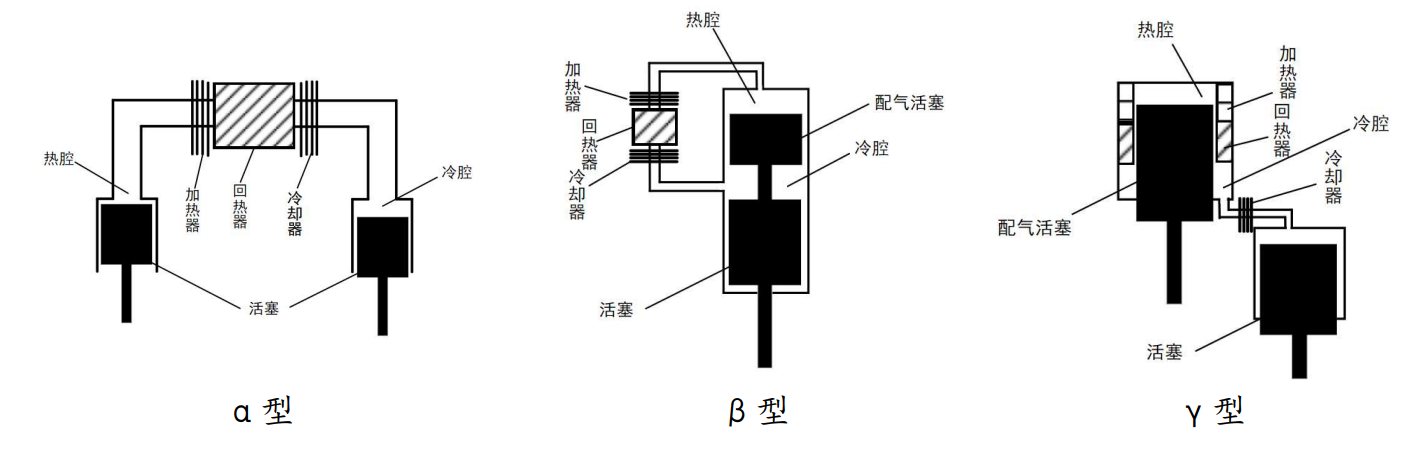
通过对于三种类型发动机的基本结构和工作原理的分析与比较,我们最终选择β型斯特林发动机进行实际设计制作。同时考虑到整体项目要求、制作难度与成本等方面,选择单作用斯特林发动机进行制作。
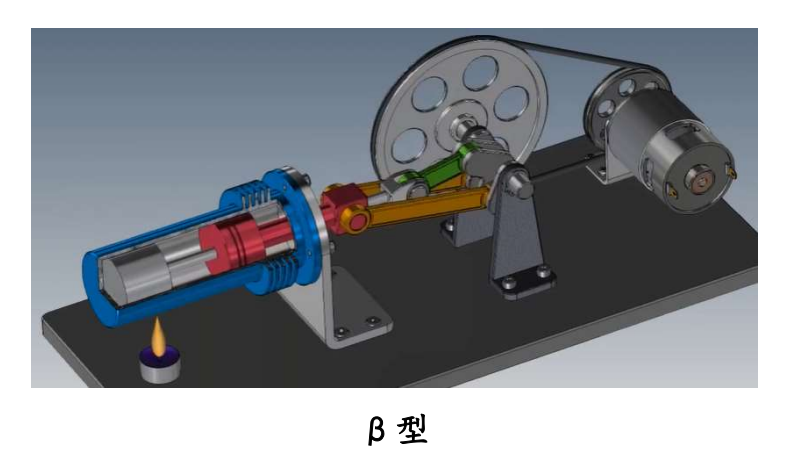
β型斯特林发动机属于配气活塞式发动机,基本结构中包含配气与动力(做功)两种活塞。其中,配气活塞只起到配气作用,并不对外做功,其上下两端压力一致,用于使工质在循环回路中来回流动;动力活塞上、下两腔气压差很大,必须进行密封处理。
斯特林发动机的基本工作原理为斯特林循环。理想的斯特林循环主要包括定温压缩、定容吸热、定温膨胀和定容放热共四个过程,其中两个为定温过程,两个为定容过程:
- 定温压缩:工作气体在活塞的压力作用下被压缩,使得气体温度降低;
- 定容吸热:压缩后的工作气体通过外部热源加热,吸收热能,温度升高;
- 定温膨胀:加热后的工作气体在活塞的推动下膨胀,产生机械功,带动发电机等设备工作;
- 定容放热:膨胀后的工作气体通过冷却器冷却,使其温度降低,回到压缩前的状态。
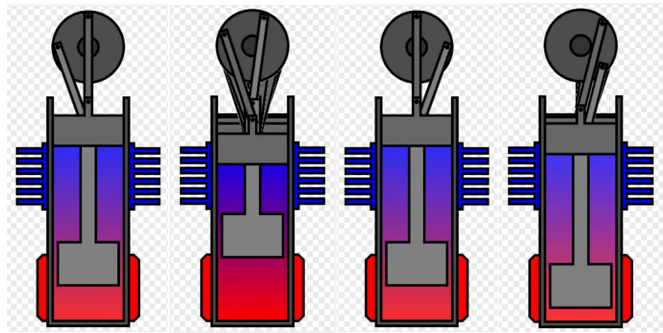
上述四个过程循环往复,共同构成斯特林循环。为了确定并验证我们所初步设计的发动机模型能否满足课题要求的最大输出功率达到0.5W,我们需要分析研究在设定条件(与实际设计结构一致)下单次斯特林循环的输出功,并通过计算结果返回迭代传动结构、尺寸与相位角等参数的设计与确定,以实现斯特林发动机单次循环输出功的最大化。
二、物理模型
本报告将给出根据我们目前设计的具体结构参数计算的单次斯特林循环输出功,并建立目标函数通过优化相位角等参数最大化单次循环输出功。
传动机构
传动机构方面,我们采用曲柄连杆机构,基本的物理模型图与我们的设计建模图如下:
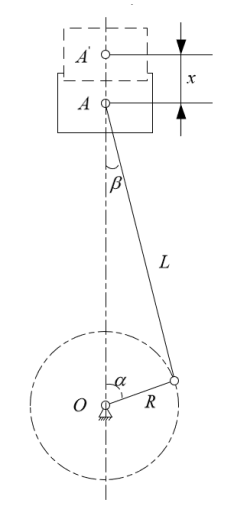
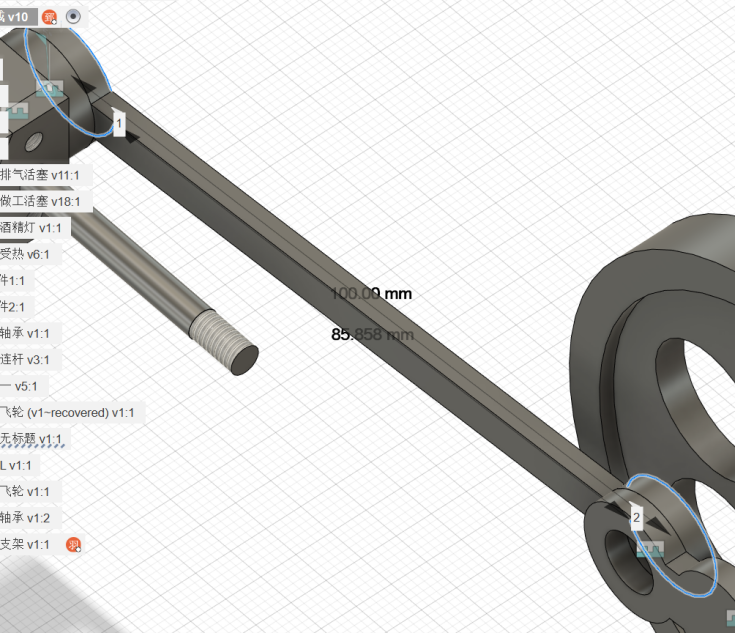
上述设计的相关参数如下:
【1】连杆比λ:
通过实际加热测试测定,四个过程状态下活塞的位置参数大致如下:
(1)定温压缩

(2)定容吸热

(3)定温膨胀

(4)定容放热

根据以上实际测试结果,可得到配气活塞行程s=20-5=15mm,动力活塞行程S=54-24=30mm,我们将其设计为与连杆机构活塞位移最大值 max(x)=2R=30mm一致,于是有曲柄半径R=15mm,再设定连杆长度L=100mm,可得到连杆比λ=R/L=0.15;
【2】转速初步设定为n=120r/min;
【3】气缸内部半径为1cm(与动力活塞一致),长度为24mm;
【4】排气活塞半径为0.8cm,长度为20mm。
热力学模型
为分析整个斯特林循环过程,结合我们以上的模型设计,给出如下热力学参数与假设:
(1)系统气密性良好、无泄漏;气缸内部半径为1cm,长度为24mm,因此未进行加热时,内部初始的工质(空气)体积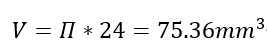 ,由此可得到工质总质量为
,由此可得到工质总质量为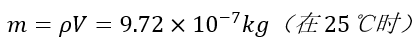 (空气密度为1.29kg/m3);
(空气密度为1.29kg/m3);
(2)工质为理想气体,气体常数为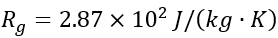 ,比热容为
,比热容为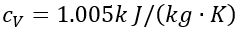 ;
;
(3)通过Ansys静态热力学仿真分析(如图),在给定特定酒精灯热源的情况下,根据设计的气缸活塞模型(加上散热片),得到工质等温膨胀及等温压缩过程的温度分别为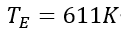 和
和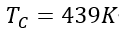 ;
;
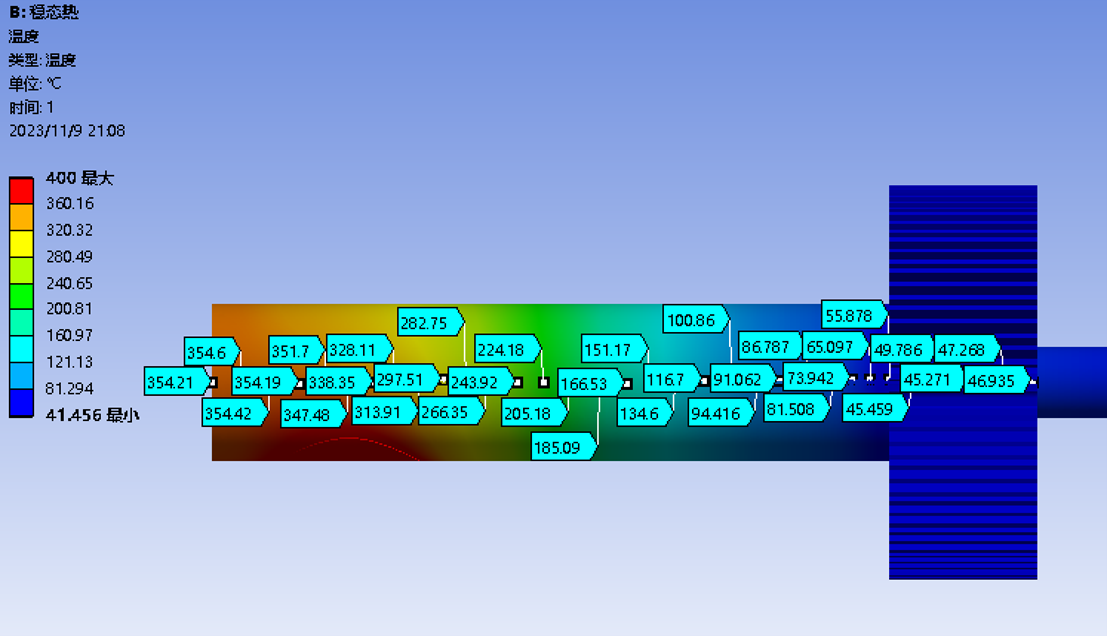
(4)系统等容加热及等容冷却过程的体积(如状态位置参数图所示)之比为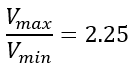 =54mm/24mm;
=54mm/24mm;
(5)忽略循环过程中的各种不可逆性。
三、循环计算分析
理论情况
在背景介绍中提到,一次斯特林循环主要分为四个过程,接下来将结合p-v图与物理模型中提到的实际参数数据对四个过程依次进行分析:
理论p-v图:
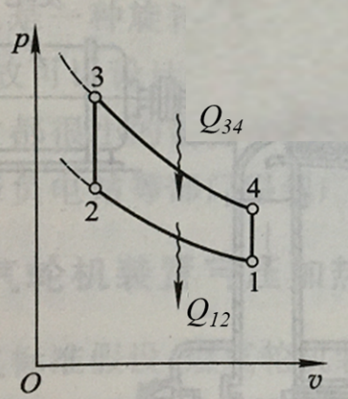
根据斯特林循环理论,有如下过程与单次循环做功计算结果:
(1)1-2:定温压缩过程
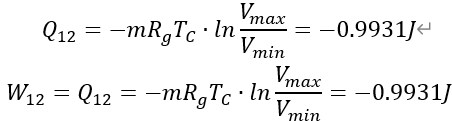
(2)2-3:定容吸热过程
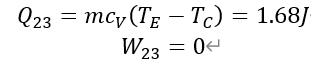
(3)3-4:定温膨胀过程
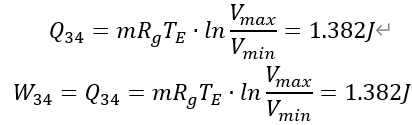
(4)4-1:定容放热过程
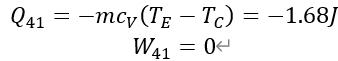
通过综合考虑由以上四个过程循环往复进行的斯特林循环,可以初步计算得出单次斯特林循环理论所作功为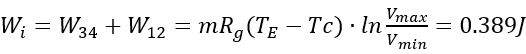
在此情况下,若设定转速为n=120r/min=2r/s,则此时该斯特林发动机的功率P=0.389*2=0.778W>0.5W,故此设计方案理论上符合项目功能要求。
特别的,如果回热器性能完全(即回热器效率ηR=1),则有Qin=Q34=1.382J,此时可计算得出该斯特林循环的单次做功效率为η=Wi/Qin=28.1%。
实际情况
无法达到理想的等温或定容过程,因此需要借助史密特理论进行计算才能更接近真实情况下的单次循环做功大小。
基于史密特理论,暂时设定相位角为90°,可以得到实际中的p-v图如下(设定气缸内气体压强最小值即初始压强pmin为标准大气压=100kPa):
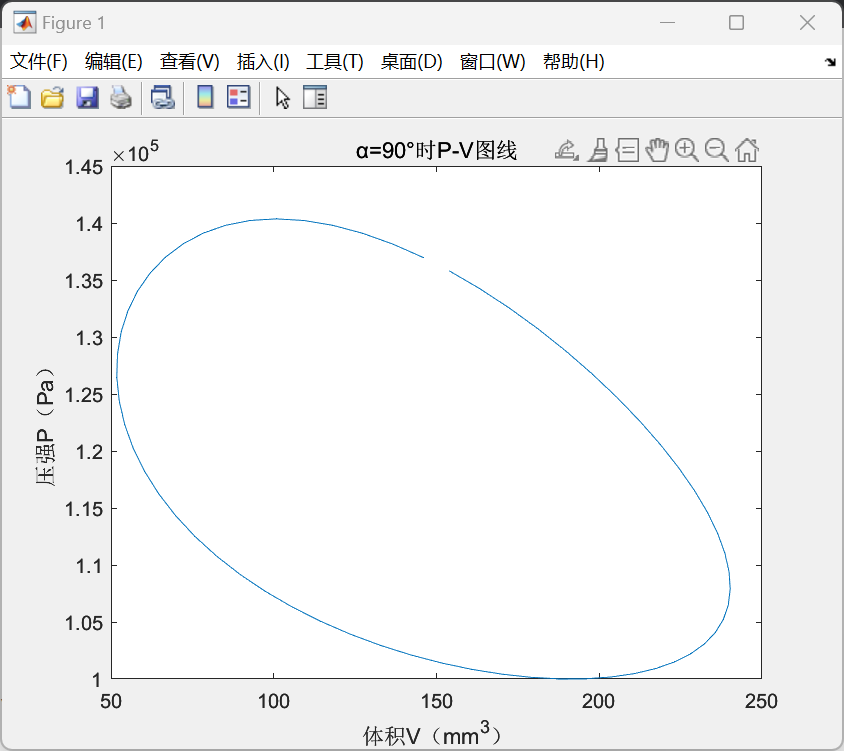
根据理论推导公式,编写代码如下:
1 | afa=pi./2; |
通过运行上述代码段,可以得到如上图所示的p-v图线,并计算出此时单次斯特林循环的实际做功大小W=0.1429J。
在此情况下,若设定转速为n=120r/min=2r/s,则此时该斯特林发动机的功率P=0.1429*2=0.2858W<0.5W,故此设计方案理论上暂不符合项目功能要求;但若增加转速至n’=P0/W=3.5r/s=210r/min,即可满足设计要求。
四、优化
在上述的设计过程中,我们将曲柄连杆机构中曲柄的半径设计为活塞在气体膨胀压缩过程中运动的最大距离(即行程)的一半,并设定相位角(排气器活塞与动力活塞的相位差角度值)为90°(依据已有的设计经验)。事实上,通过分析史密特理论的计算式不难发现,随着相位角的改变,最终计算出的单次循环所作功也发生改变,因此在优化时需要通过绘制W-α图像直观反映二者间的关系,并找到合适的相位角α值以最大化单次循环所作功W。
以下是设计的MATLAB代码与绘制的对应图像:
1 | afa=0:0.1:pi*2; |
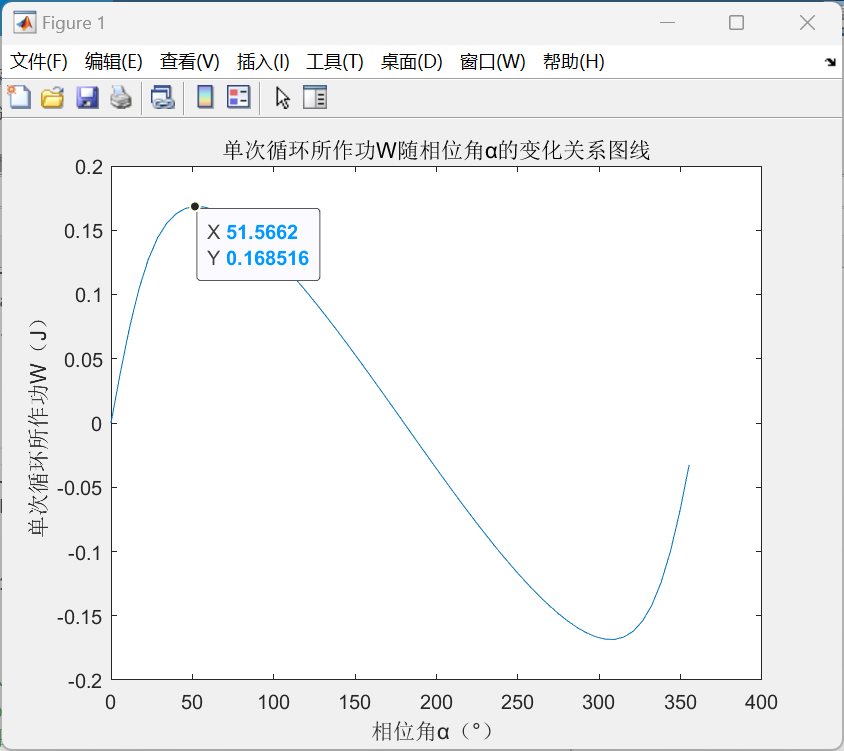
由图像可见,当相位角α=51.6°左右时,单次循环所作功达到最大值Wmax=0.169J,较原先相位角为90°的方案有所提升,只需要转速达到nmin=P0/Wmax≈2.96r/s=178r/min即可满足设计功能要求,实现了优化效果。
五、总结
在本次课题任务中,借助了热力学方法研究气缸内的封闭气体,从而对于我们小组初步设计的β型斯特林发动机模型的动力(做功)性能进行了一定的评估分析,并在此基础上通过MATLAB工具绘制函数图像,通过对于目标函数的优化以指导我们进行结构上的进一步改进以提升性能。
在热力学分析过程中,从斯特林循环的四个基本环节入手,结合我们设计的气缸、活塞等尺寸参数、实际测试得到的经验参数以及简单的传动机构设计(曲柄连杆机构),从理论分析逐步逼近实际,最终借助一阶的史密特等温分析方法理论实现了较为接近实际的计算模拟,得到了单次斯特林循环对外做功的数值解从而给出达到目标功率所需要设定的飞轮转速。
同时,在此基础上,通过改变相位角等参数,基于史密特理论中单次循环做功的计算公式,得到了可以进行优化(求极值)的目标函数,并得到了当前尺寸参数下的最大单次循环做功及其对应的相位角,有效实现了基于理论计算的迭代与优化。
课题:斯特林发动机热力循环计算及分析