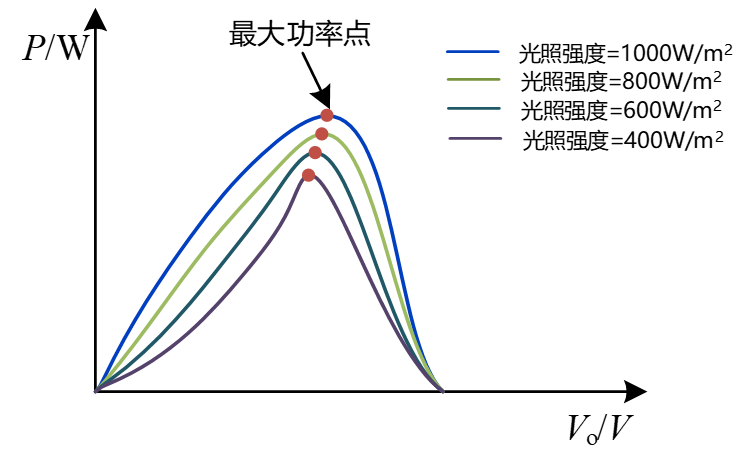摘要 本项目围绕直流电源调控的自动调光控制系统展开研究与设计，系统性地探讨了Buck变换器的基本原理、建模方法、性能分析及其实验验证过程。在硬件设计方面，基于STM32处理器，选择了高性能的元器件并通过合理的电路拓扑实现高效的能量转换；在软件控制算法方面，采用PID闭环控制，并结合自动控制原理中的经典控制理论，利用PSIM与MWorks等仿真与科学计算工具，对控制系统的时域响应、频域特性和稳定性进行了详尽分析，进而通过参数优化与校正环节设计显著提升了系统的响应速度和稳态性能，同时也验证了闭环控制系统在动态性能、抗干扰能力和输出精度方面的显著优势。此外，通过实验测量与仿真结果对比，探讨了电路寄生参数对系统性能的影响，为后续优化提供了理论依据。在基于光敏电阻的自动调光功能模块中，结合蓝牙通信接口实现了系统的智能化控制，同时对于自动调光系统进行外观设计，赋予产品更多的人文关怀与实用价值；在光伏板最大功率点跟踪（MPPT）功能模块中，根据MPPT的原理与基本思想设计了相应的控制算法，并在实验中成功控制光伏板输出功率，使其约等于负载消耗功率，完成了不同光照强度下最大功率点的跟踪。最后，对于该自动控制系统的设计成果及其在实际应用中的可行性与局限性进行总结，并对未来可能的优化方向和工程实现前景提出了展望。
关键词： Buck变换器；PID闭环控制；自动调光；光伏MPPT
1 课程涉及理论基础和STM32简介 1.1 自动控制原理简介 在科学技术飞速发展的今天，自动控制技术和理论已经成为现代社会不可缺少的组成部分。自动控制技术的应用不仅使生产过程实现自动化，从而提高了劳动生产率和产品质量，降低了生产成本，提高了经济效益，改善了劳动条件，使人们从繁重的体力劳动和单调重复的脑力劳动中解放出来；而且在人类征服大自然、探索新能源、发展空间技术和创造人类社会文明等方面都具有十分重要的意义。
自动控制理论是研究关于自动控制系统组成、分析和综合的一般性理论，是研究自动控制共同规律的技术科学。自动控制是在人不直接参与的情况下，利用外加的自动控制设备或装置（控制装置或控制器），使机器、设备或生产过程（统称为被控对象）的某个工作状态或参数（被控量）自动地按照预定的规律运行，使机器的动作、设备的运转、生产过程的状态能够自动地在一定的精度范围内按照给定的规律变化。学习和研究自动控制理论是为了探索自动控制系统中变量的运动规律和改变这种运动规律的可能性和途径，为建立高性能的自动控制系统提供必要的理论依据。
1.2 本项目所涉及的经典控制理论内容
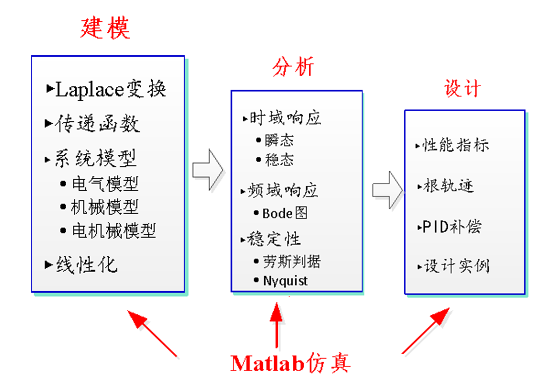
本项目从经典控制理论的基本原理与概念出发，以Buck变换器这一单输入-单输出的线性系统作为研究对象，利用微分方程、Laplace变换与传递函数等数学工具建立系统的数学模型，并基于时域分析、频域分析以及根轨迹法等多种分析方法对于系统的稳定性与响应特性进行详细分析，从而针对特定的性能指标进行对应的校正设计，通过引入PID控制器并调控其参数以改变系统的频率特性从而满足给定的各项性能指标，使得整个闭环控制系统能够兼具稳定性、快速性与准确性。
1.3 STM32处理器介绍 控制核心是控制系统中的重要组成部分，用于计算、解析各种数据，并执行相应的控制算法。芯片选型的设计直接决定了控制板的性能和功能。STM32是由意法半导体公司（ST）推出的基于Arm Cortex-M处理器内核的32位微控制器，专为要求高性能、低成本、低功耗的嵌入式应用设计，集实时功能、数字信号处理、低功耗/低电压操作、连接性等特性于一身，同时还保持了集成度高和易于开发的特点，基于行业标准内核，提供了大量工具和软件选项以支持工程开发，非常适用于小型项目或端到端平台。
本项目选用的处理器STM32F103C8T6作为中等容量高性能系列MCU，集成了工作频率为72MHz的高性能Arm Cortex-M3 32位RISC内核、高速嵌入式存储器（高达128KB的Flash存储器和20KB的SRAM存储器），以及大量连接至2条APB总线的增强型I/O与外设，具有36引脚至100引脚等6种不同的封装类型。所有器件均提供2个12位ADC、3个16位通用定时器、2个PWM定时器以及标准和高级通信接口：多达2个I2C和SPI、3个USART、1个USB和1个CAN。器件的工作电压为2.0V至3.6V。该处理器的工作温度范围为-40℃到+85℃，可扩展至-40℃到+105摄氏度。这些特性使得该处理器成为各种应用的理想之选，也能很好满足本项目对于控制器的性能需求。
1.4 本章小结 本章主要介绍了本课程相关的自动控制理论基础，针对本项目涉及到的经典控制理论框架进行了简要概述，同时对于本项目所选用的控制核心——STM32处理器进行简单介绍，重点分析了我们采用的STM32F103C8T6处理器的性能特性并给出选型原因。这为本课程项目提供了整体框架，并从理论上对后续项目的具体实施给出了方向性的指引。
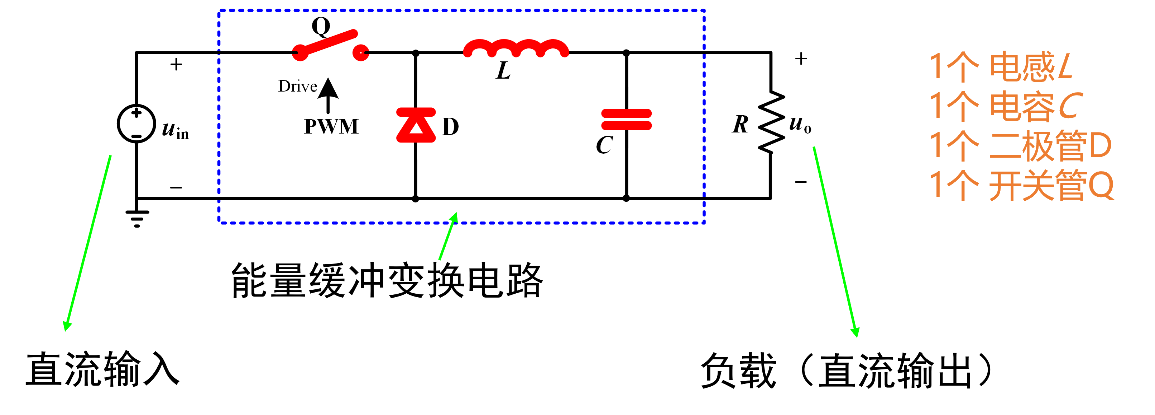
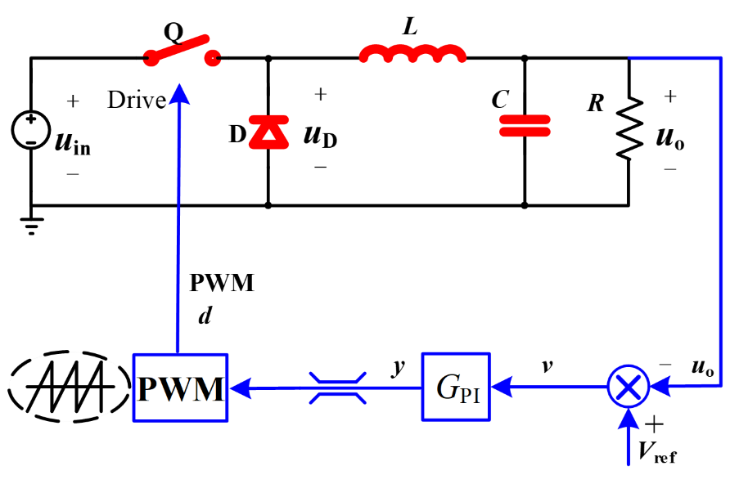
2 直流Buck变换器设计与调试 2.1 Buck变换器拓扑原理分析 Buck（降压式）变换器是一种输出电压≤输入电压的非隔离直流DC-DC变换器，其中输入电流为脉冲式的，而输出电流为连续的低纹波直流电压。Buck变换器实现的稳态输入输出关系为：
可以看到，在能量缓冲变换电路中，主要由如下三个部分组成：
电感L与电容C实质上构成了一个二阶低通滤波器，通过滤除开关频率交流分量而仅保留其直流分量，得到平直的输出电压U0；
脉冲宽度调制（Pulse Width Modulation，PWM）产生方波电压控制开关管Q的导通；
二极管D为电感电流提供续流回路。
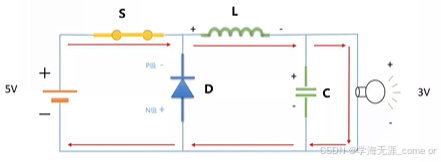
Buck变换器主电路整体的工作逻辑如下：
当开关管Q驱动为高电平时，开关管导通，储能电感L被充磁，流经电感的电流线性增加，同时给电容C充电，给负载R提供能量；
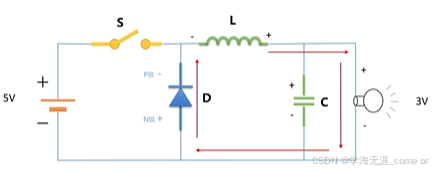
当开关管Q驱动为低电平时，开关管关断，储能电感L通过续流二极管D放电，电感电流线性减少，输出电压靠输出滤波电容C放电以及减小的电感电流维持。
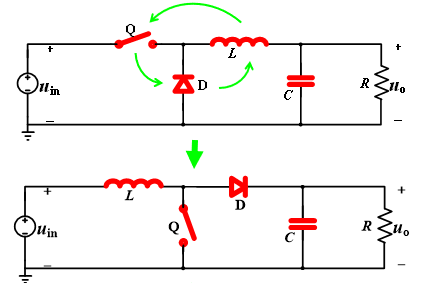
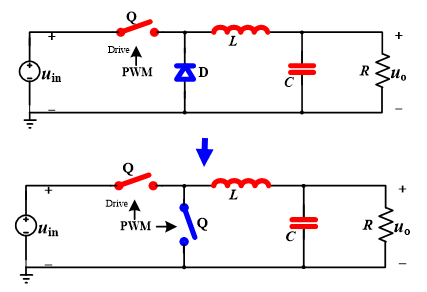
事实上，对于该电能变换器，可以通过更改个别元器件的种类、接入方式与顺序，实现搭建具有不同功能的电能变换电路，即Buck变换器的拓扑原理。下面列举几种常见的拓扑电路：
升压变换器：
降压同步整流变换：采用互补工作模式，可减小损耗
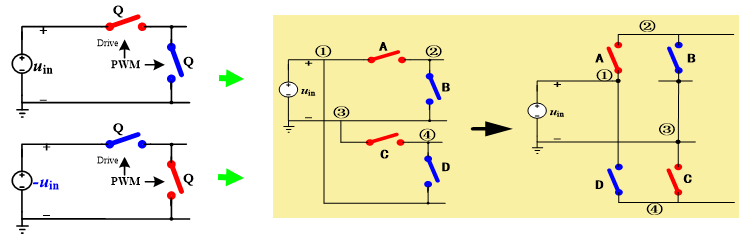
H桥DC-AC逆变器：开关管部分串联构成双极性交流电压源
闭环PWM控制：可以在原有Buck电路基础上增加闭环环路，通过PWM调配开关管Q的导通与否，从而实现对于输出电压的控制，使系统能够更加”稳”、”快”、”准”地得到期望的输出。目前的控制器选择主流为PID控制器，根据不同的指标又可将闭环控制系统分为不同类别：若根据控制对象分类，则可分为电压控制与电流控制；若根据接收调控信息的时间先后分类，又可分为反馈控制与前馈控制；根据其他的分类标准，还可分为线性/非线性控制、平均/纹波控制、模拟/数字控制……在此不一一列举。
2.2 Buck变换器元器件参数选择 在Buck变换主电路中，对电路参数进行如下设定：
输入电压
输出电压
占空比
电源转换电压：12V、15V、5V、5V（隔离）
电感
电容
工作频率
首先，为满足电源转换与单片机供电的需求，需要在电源直接引入Buck电路前先接入电源模块，涉及到的元器件及相关参数如下：
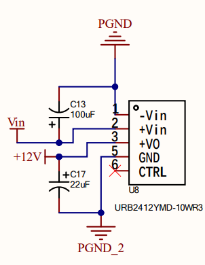
URB2412YMD-10WR3电源模块：降压模块，将电源提供的输入电压（最大35V，本实验中为15V）转换为12V输出，提供0.83A的电流；
CW7805线性稳压器：将12V输入电压转换为稳定的5V输出电压，并将输出电流转换成1A，分输入、输出与接地三端，主要用于使线性的输出电压稳定；
A1215S-2WR3电源模块：升压模块，将12V输入转换为±15V，适合供给双电源运放电路，本实验中主要用于为采样电路（滤波器）供电；
IB1205S-2W电源模块：降压模块，将12V输入转换为5V，通常用于低功耗电路的供电，本实验中主要用于光耦（与驱动）电路的供电。
贴片MOS管NCE0130KA：VDS=100V，VGS=10V
贴片电感：色环直插型，100uH
贴片铝电解电容：330uF，±20%，耐压50V，两个并联达到设定660uF
电流传感器CC6920SO-5A：初级电流测量范围-5A~5A，供电电压5V
电压传感器LV25-NP：初级电流测量范围10-500V，供电电压±15V
其中，电容与电感均采用贴片形式的原因主要有以下几点：
【1】 体积小且便于贴装，适合电路的高集成度需求；
【2】 贴片元件引线较短，寄生电感和电容较小，可提高电路的高频性能；
【3】 贴片元件的散热性能通常较好，有助于提高电路的可靠性；
【4】 贴片元件可以有效减小电磁干扰，提高电路的稳定性。
除此之外，由于本实验采用的主控STM32输出能力有限，无法直接驱动管子开关，因此还需要采用光耦和驱动电路为管子提供驱动信号，涉及到的元器件及相关参数如下：
IR21844S驱动：栅极驱动供电范围10-20V
光耦-逻辑输出6N135：5V供电，光耦隔离
运算放大器AD823ARZ：最大输入偏置电流25pA，低失真−108dBc
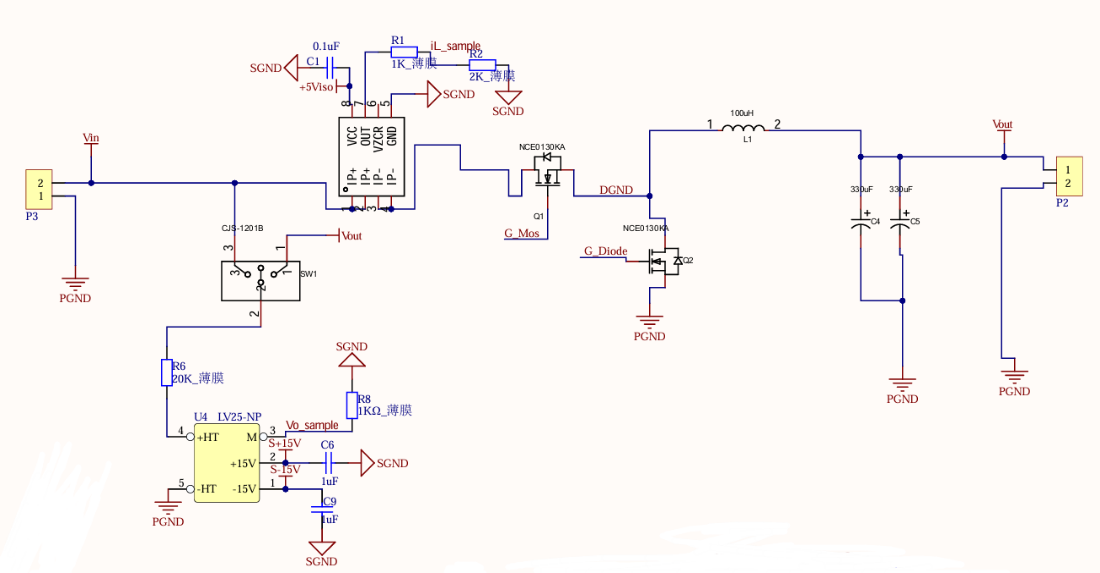
2.3 Buck变换器实物设计与调试 在Buck变换主电路设计时，选择不对Buck变换器的电路部分进行拓扑，而在闭环PWM控制电路中采用平均电压模式进行控制。本项目采用的实验电路板主要包括Buck电路基本器件、开关管驱动、辅助电源以及采样电路（信号调理电路），实验时将元器件焊接至电路板上并分别调试各模块功能。
2.3.1 主电路设计与调试
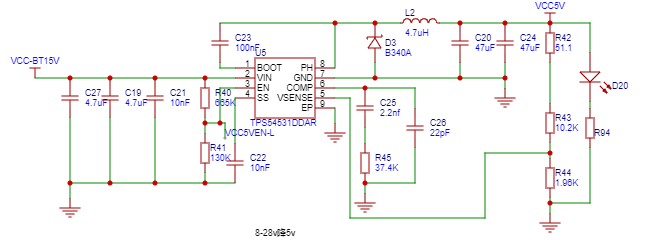
该电路是一个典型的降压型 DC-DC 转换器，其工作原理是通过开关管 Q3 的高速开关动作，将输入电压V_IN转换为期望的输出电压V_OUT。当开关管Q3导通时，输入电压通过 L2、L3和负载形成电流回路，电感存储能量，同时为负载供电；当 Q3关断时，续流二极管 D4 提供电流通路，电感释放能量维持负载电流的连续性。控制器 U6根据反馈电压（通过分压电阻 R8 反馈的V_OUT）与参考电压之间的误差，实时调节 Q3的导通时间（占空比），从而实现输出电压的稳定调节。两级电感 L2 和 L3以及滤波电容 C9、C15进一步平滑输出电流和电压，减少高频纹波，确保输出电压的稳定性和低噪声特性。
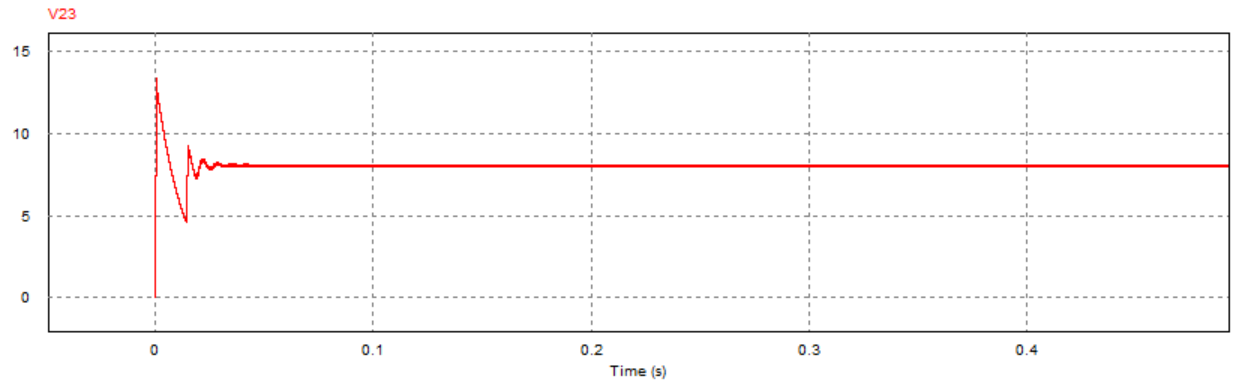
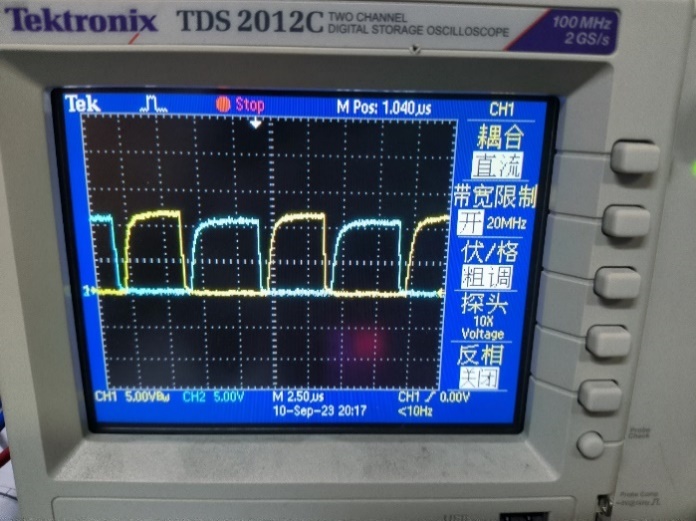
经过调试，Buck降压模块主电路可正常实现功能，在参考输入方波幅值为8V、占空比为50%的情况下能够输出占空比为50%、幅值在8V左右（实际约为8.5V）的方波。
2.3.2 控制电路供电设计与调试
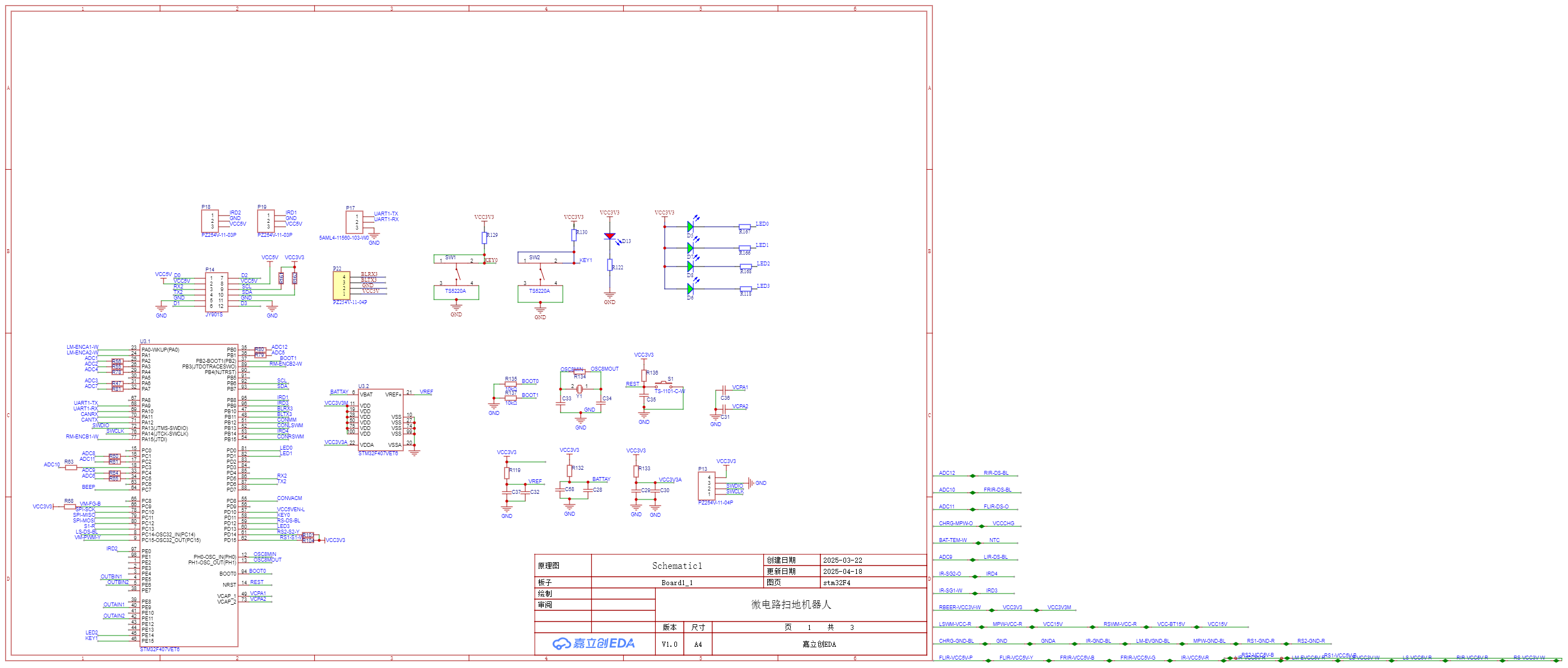
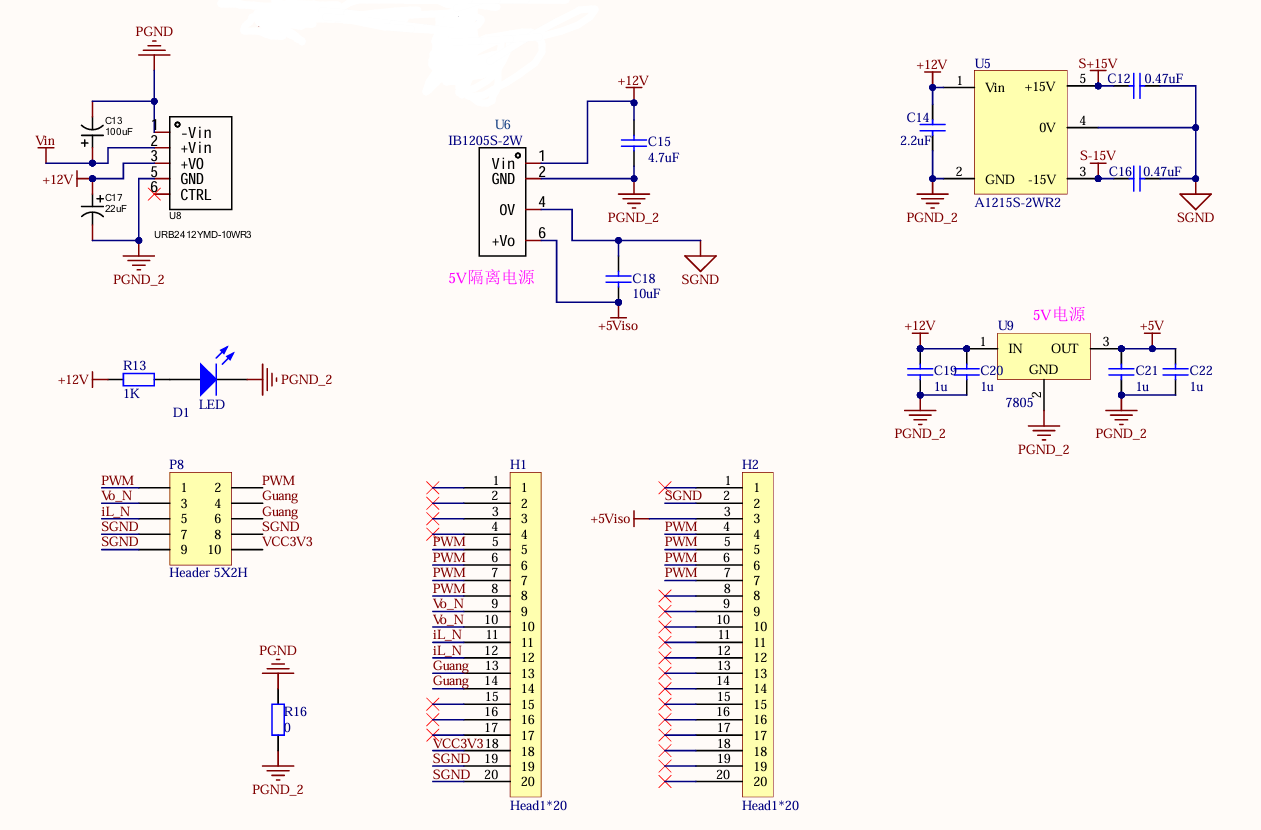
如图所示为STM32主控芯片供电电路（电源模块）以及单片机内部所使用的接口引脚图，同时将大部分未使用的引脚通过排针引出以供后续拓展功能开发。
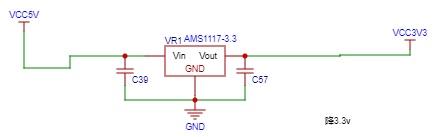
在STM32主控芯片供电电路中，包含两个级联的线性稳压器，用于将高电压逐级稳压到所需的5V 和 3.3V。上半部分采用 CJ7805稳压器，将输入电压V_IN转换为稳定的5V输出，通过输入电容C2和C1滤波降低输入纹波，稳压器通过内部反馈电路调节输入电压，使输出稳定在5V，同时通过输出电容C3滤除高频噪声，进一步平滑输出电压。下半部分采用
调试流程：取下单片机核心板—>接入负载100欧姆—>单片机输出PWM—>观测PA8端口波形—>观测驱动芯片输出端口波形—>上主电24V—>检测辅助电源输出电压—>检测输出电压—>根据占空比计算输出电压是否正常—>完成
经调试，该部分模块可正常工作，为STM32主控芯片提供稳定的5V电压：
2.3.3 驱动电路设计与调试
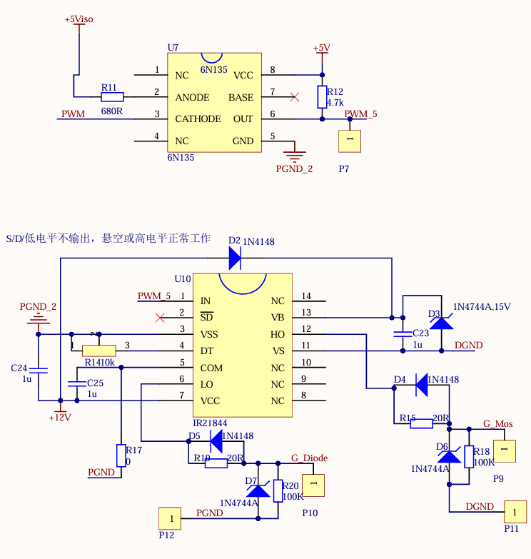
如图所示，驱动电路为已有的STM32输出提供了合适的电压和电流驱动功率器件，而如果直接使用STM32输出驱动，可能会超出其输出能力或不能实现良好的电气隔离，导致驱动失败或损坏器件，输出信号不稳定。使用光耦和驱动电路则可以更好地实现电气隔离，从而防止高压或大电流对控制电路的干扰或损坏，保护STM32免受高电压或大电流的影响，提高系统工作可靠性。
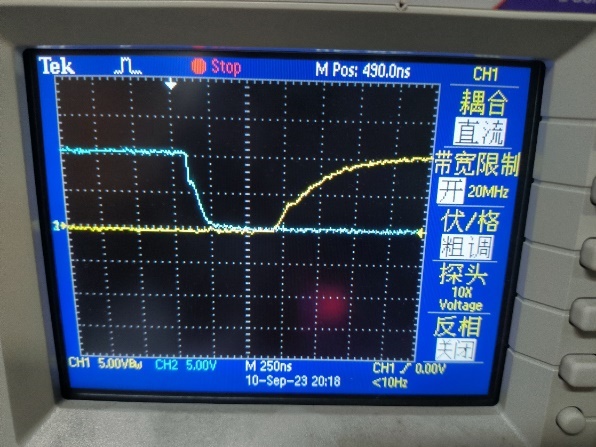
调试时，先切断仿真器供电，将单片机供电切换为主电路辅助电源供电；单片机烧录输出电压控制程序后，接入后端负载，再上主电，观测输出电压。经调试，驱动电路可正常工作。
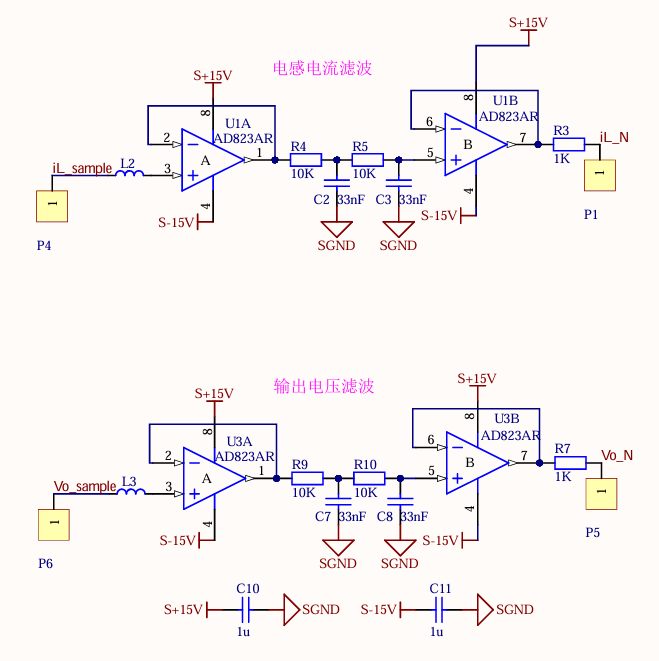
2.3.4 电压和电流采样调理滤波设计与调试
该电路是一个基于运算放大器的电压比较和分压检测电路，主要功能是将输入电压V_OUT通过电阻分压后与基准电压比较，并输出相应的信号V_S。该电路可用于电压监测或过压保护等场景，通过调整R1 和 R2 的比例，可以设置分压电压，从而灵活设定输入电压的触发阈值。
具体工作原理如下：输入电压$V_{OUT}$经由电阻R1和R2分压后，产生一个分压电压，该电压送入运算放大器U5的反相输入端（引脚2）。运算放大器的非反相输入端（引脚 3）通过稳压二极管 D2提供一个固定的基准电压（3.3V）。当分压后的电压低于基准电压时，运算放大器输出高电平；当分压电压高于基准电压时，运算放大器输出低电平。电容C7和C16用于滤除输入和输出的高频噪声，保证比较过程的稳定性。
调试时，使用仿真器给单片机供电，以调试PWM波形输出是否正常；烧录开环测试程序之后，使用示波器或者上位机观测电路板PA8端口是否正常输出PWM波形。经调试，可对输入信号正确采样并输出对应波形，说明采样模块正常工作：
2.4 本章小结 本章主要介绍了直流Buck变换器的基本工作原理及其拓扑变换，并根据选定的主控芯片STM32F103C8T6以及设定的电路参数进行了基本元器件的选型与电路原理图及PCB电路板的设计，确定电路主要包括Buck降压变换主电路、控制电路供电辅助电源模块、驱动电路以及采样电路（信号调理电路）四个模块；在焊接时对各个模块依次进行焊接与调试，保证各模块均可以正常工作，以便于后续闭环控制实现时STM32主控控制模块与代码的设计与测试。
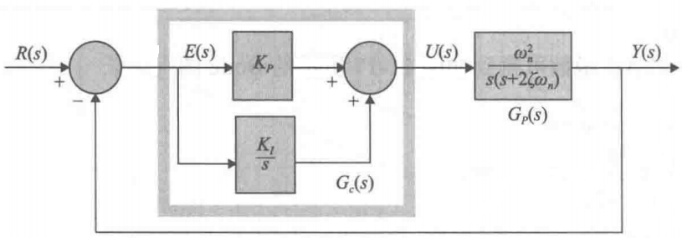
3 直流Buck变换器建模 3.1 Buck变换器闭环控制原理分析 Buck变换器闭环控制系统主要由以下几个部分组成：
误差放大器：将参考电压V_ref与实际输出电压V_OUT比较，生成误差信号；
补偿网络：对误差信号进行处理（例如，PI或PID控制），以提高系统稳定性和动态性能；
PWM调制器：将补偿后的控制信号转换为开关元件的占空比D;
采样电路：对输出电压 V_OUT进行实时采样。
整个闭环控制系统的工作过程如下：
输出电压采样：通过分压电路对输出电压V_OUT进行采样，得到反馈电压V_fb;
误差检测：误差放大器将参考电压V_ref与反馈电压V_fb比较，产生误差信号
误差调节：误差信号经过补偿网络调节，生成调节信号V_ctrl，此信号决定PWM占空比；
PWM调制：调制器根据调节信号V_ctrl生成控制信号D，驱动开关元件；
电感电流调节：开关元件的导通时间决定电感电流的充电时间，从而控制输出电压。
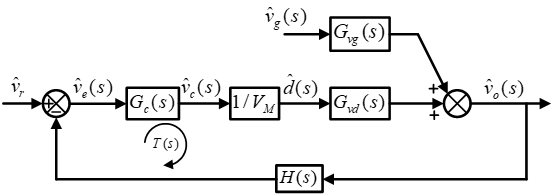
从系统传递函数的角度考虑，根据系统框图与元件特性，可计算其开环传递函数与特征方程：
（1）G_c(s)为PI环节， PI调节器为：
$$
$$
$$
$$
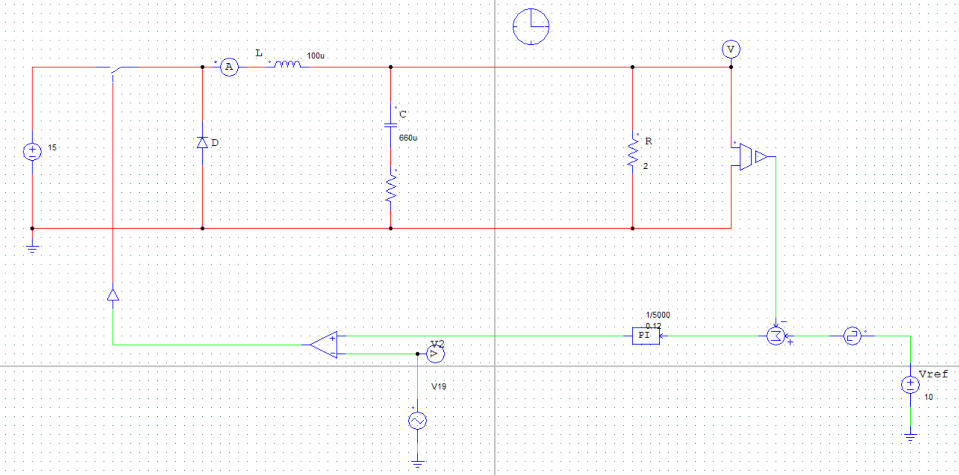
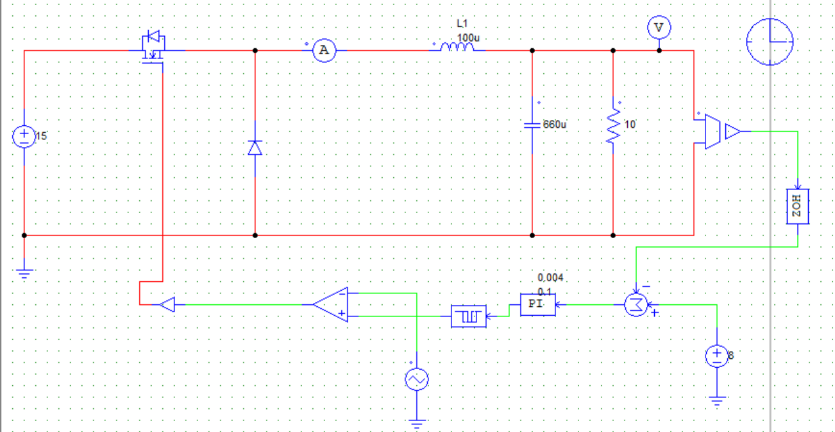
$$
3.2 Buck变换器PSIM仿真（开环+闭环） 利用PSIM软件进行电路仿真，根据实际电路结构搭建仿真电路图，并将电路各元件实际参数代入（PI控制器参数：K_p = 0.1，tao = 0.004）：
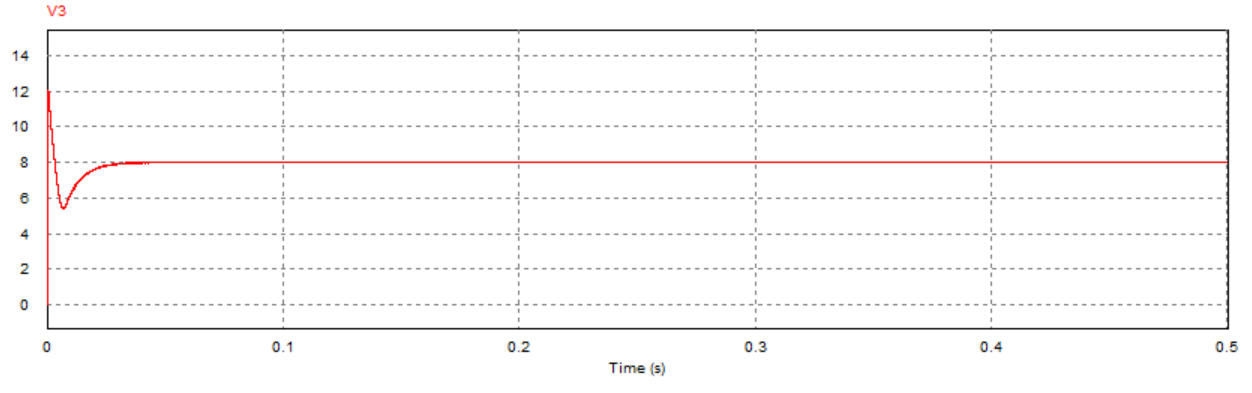
运行仿真程序，可得到输出电压的仿真结果：
对比开环与闭环控制系统的输出电压仿真结果可以发现，尽管两个系统都能在短时间内达到稳定的输出电压，但显然闭环控制系统到达稳态的速度更快且震荡更小，稳定后的电压也更接近参考电压8V（约为7.95V）。这说明闭环控制系统具有更快的响应速度与更好的稳定性和准确性。
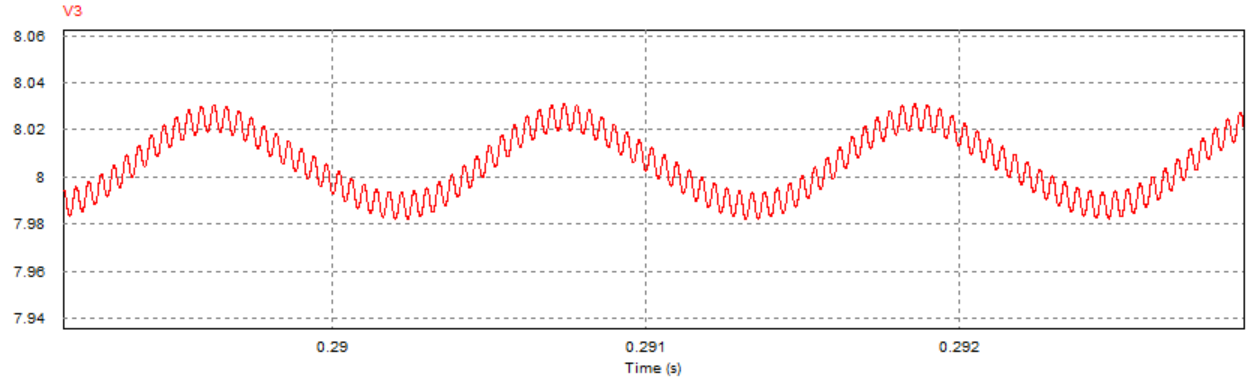
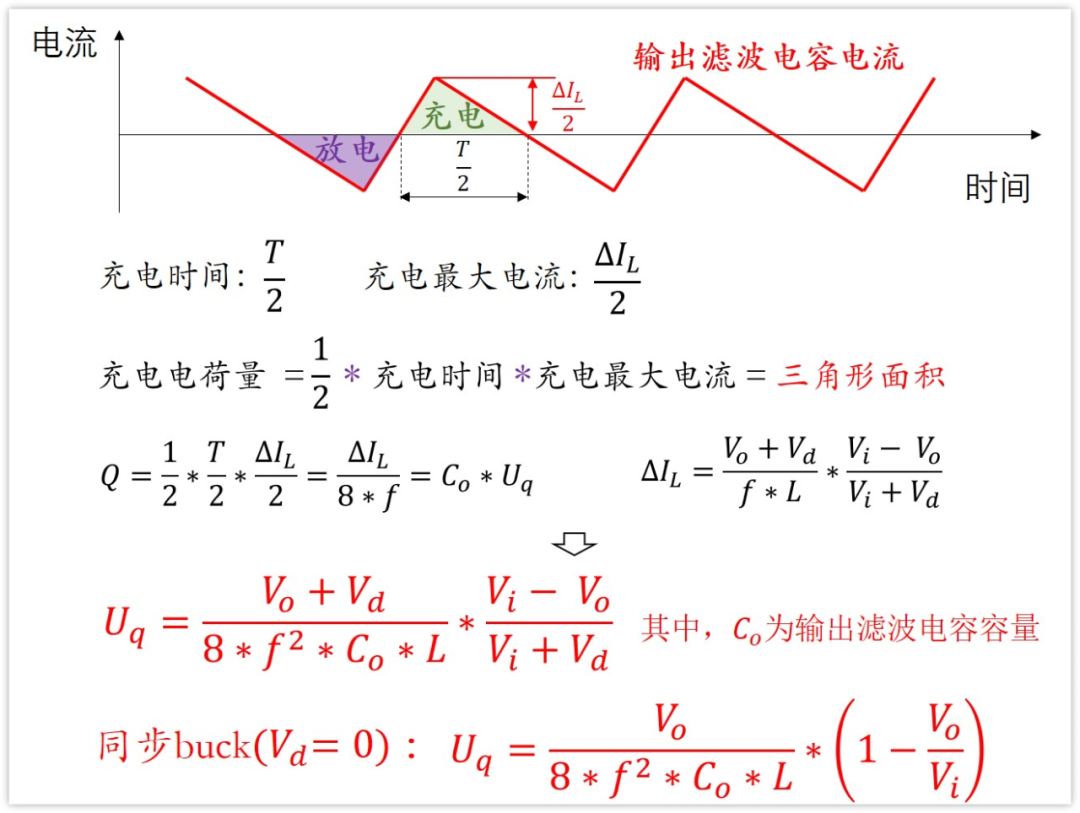
3.3 输出电压纹波计算（仿真+实验）
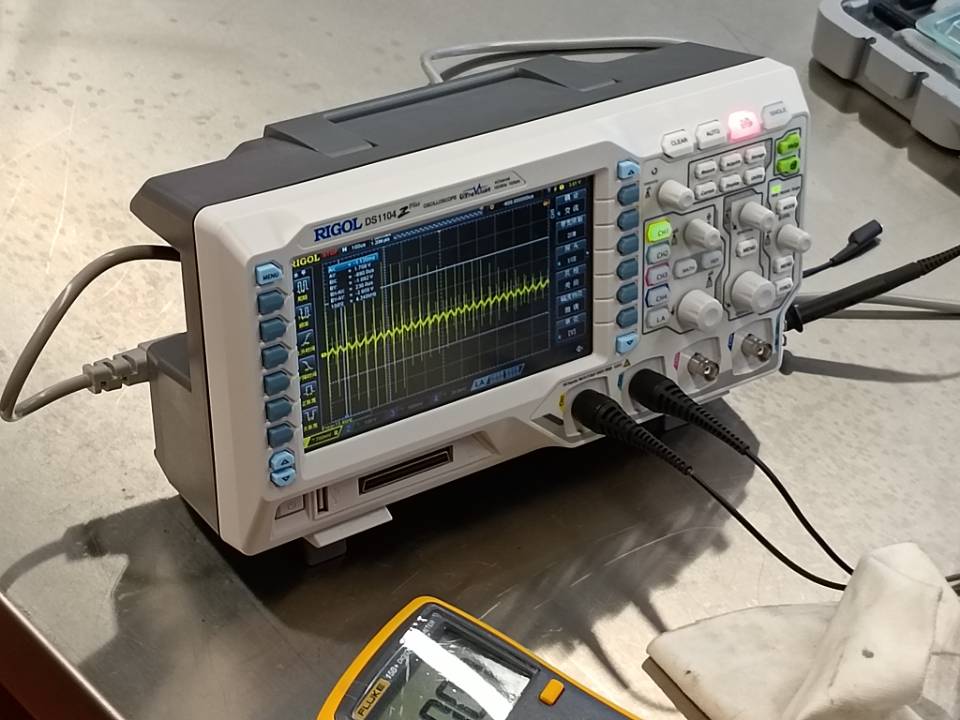
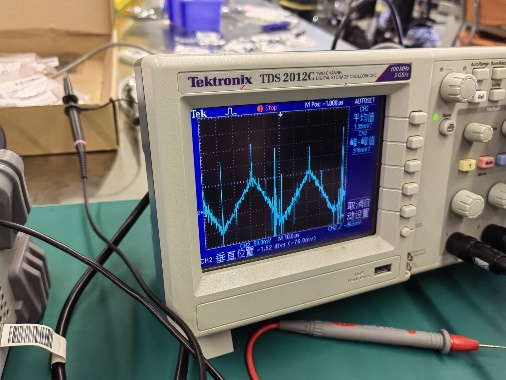
首先进行Buck变换器的开环控制实验，并通过示波器观察其输出电压的纹波波形。可以看到，输出波形峰值
可得到输出电压纹波的仿真结果：
可以看到，输出电压信号的震荡波形与实际电路示波器显示的纹波形状一致且震荡幅度大致相同。
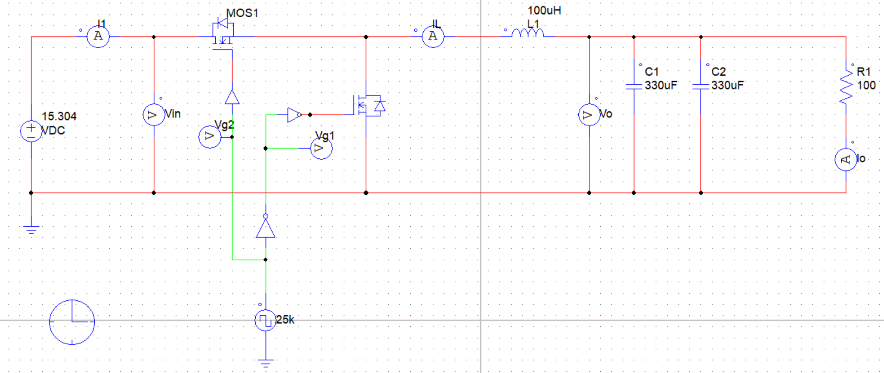
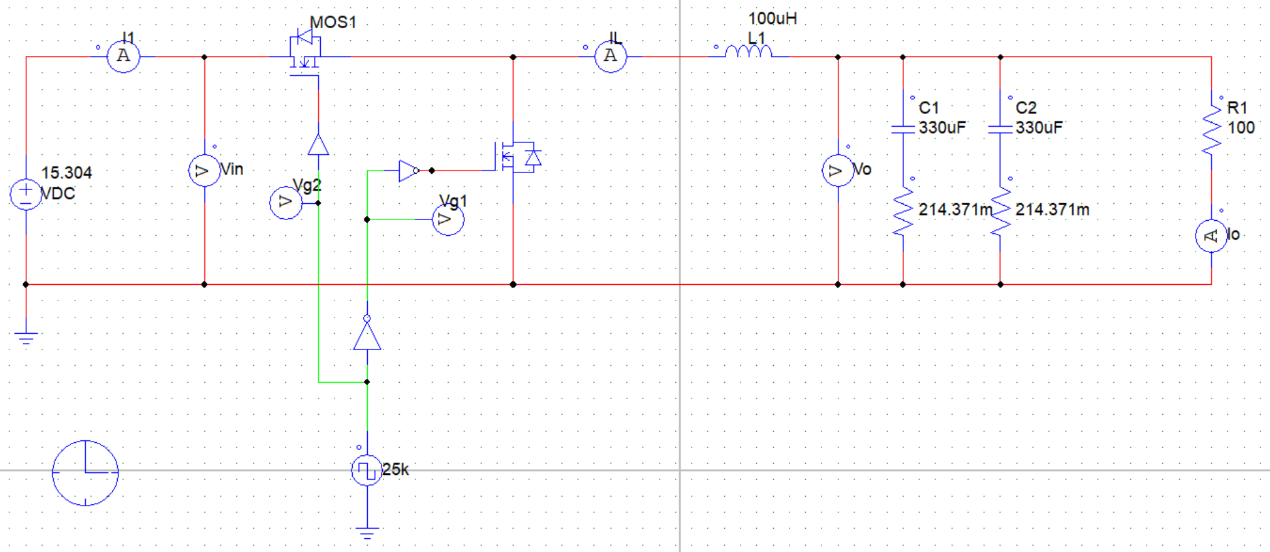
3.4 电容寄生电阻计算（仿真+实验） 在Buck变换器开环控制实验中，通过万用表测量得到输入电压V_i= 15.304V，输出电压均值V_o = 7.537V：
除了给定的元件参数之外，为对直流Buck变换器进行精确建模，考虑到电容的寄生参数可能对系统有较大影响，故特别计算其寄生电阻阻值ESR：
结合
$$
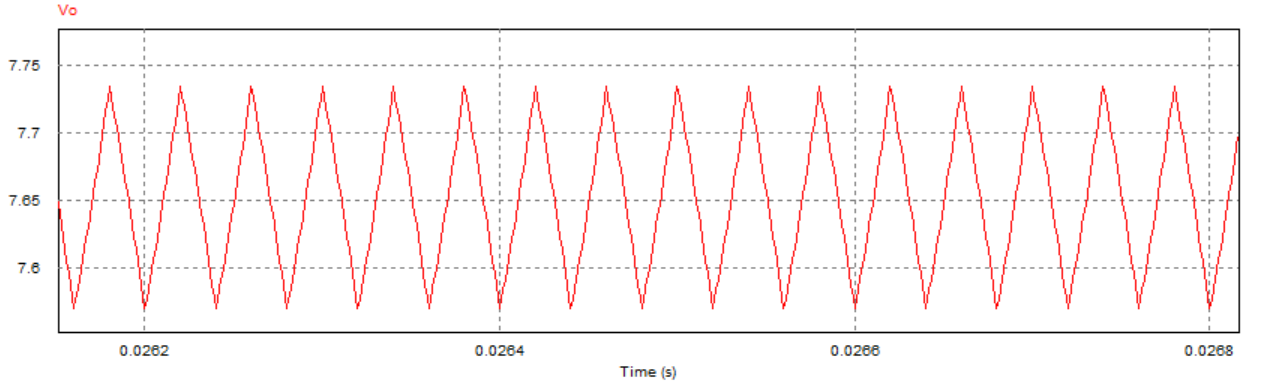
得到的输出电压仿真结果如下图所示：
可以看到，仿真结果中输出电压的均值约为7.65V，与实际的测量结果
3.5 本章小结 本章主要介绍了直流Buck控制器及其闭环控制系统的建模过程，通过分析Buck电路中的元件特性及闭环控制的各个环节，实现控制系统的数学建模，得到系统的开环传递函数与特征方程；同时结合Buck控制器开环控制实验的实际测量结果，关注到电容寄生电阻对于系统输出的重要影响，并通过输出电压纹波的相关特性对其进行计算，搭建PSIM电路仿真模型观察修正前后的仿真结果，发现引入寄生电阻后的仿真结果与实际实验波形输出基本一致从而说明考虑寄生电阻的必要性。除此之外，还分别搭建了Buck变换器的开环与闭环控制系统PSIM仿真电路并对比输出电压仿真结果，可以发现闭环控制系统具有更好的动态响应性能，其稳定性、快速性与准确性均优于开环控制系统。
4 直流Buck变换器控制性能分析 4.1 直流Buck变换器劳斯稳定判据分析 基于3.1节得到的开环传递函数与系统特征方程，可利用劳斯判据给出系统稳定的PI控制器比例系数K_p临界条件：
根据系统特征方程可给出如下劳斯表：
根据劳斯判据，要使得系统稳定，需同时满足如下条件：
$${in}K {p} > 0
$$
$$
$$
$${in}K {p}(\tau s + 1) + \tau sV_{M}\left( LCs^{2} + \frac{L}{R}s + 1 \right) = V_{M}LC\tau s^{3} + (V_{M}\frac{L}{R} + C \bullet ESR \bullet V_{in}K_{p})\tau s^{2} + (V_{in}K_{p}\tau + V_{M}\tau + C \bullet ESR \bullet V_{in}K_{p})s + V_{in}K_{p} = 0
根据系统特征方程可给出如下劳斯表：
根据劳斯判据，要使得系统稳定，需同时满足如下条件：
$${in}K {p} > 0
4.2 直流Buck变换器系统根轨迹分析（手绘+MWorks绘制） 基于3.1节得到的开环传递函数，代入数值可得：
$$
具有1个零点：
根轨迹的渐近线与实轴的夹角
\delta_{a} = \frac{\sum_{}^{}\left( - p_{i} \right) - \sum_{}^{}\left( - z_{i} \right)}{2} = \frac{- \frac{5}{33}*10^{3} + 250}{2} \approx 49.24
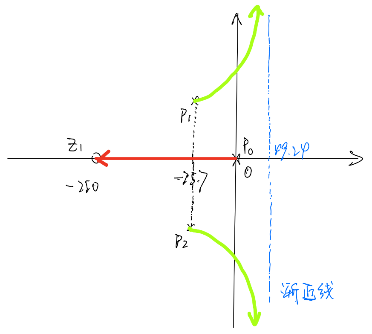
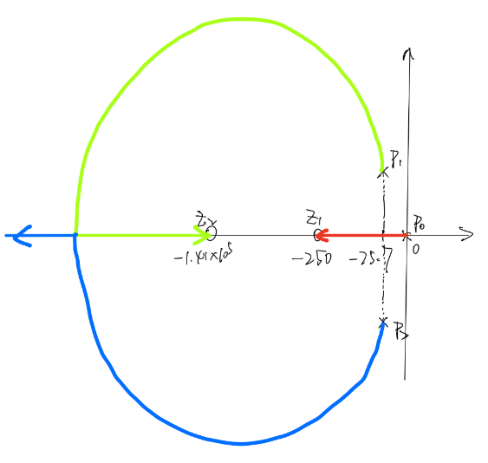
基于以上结果，可手绘根轨迹草图如下：
编写如下MWorks代码：
1 2 3 4 using TyControlSystemss=tf('s' ); G=(s+250 )/(s*(6.6 *10 ^(-8 )*s*s+10 ^(-5 )*s+1 )); rlocus(G);
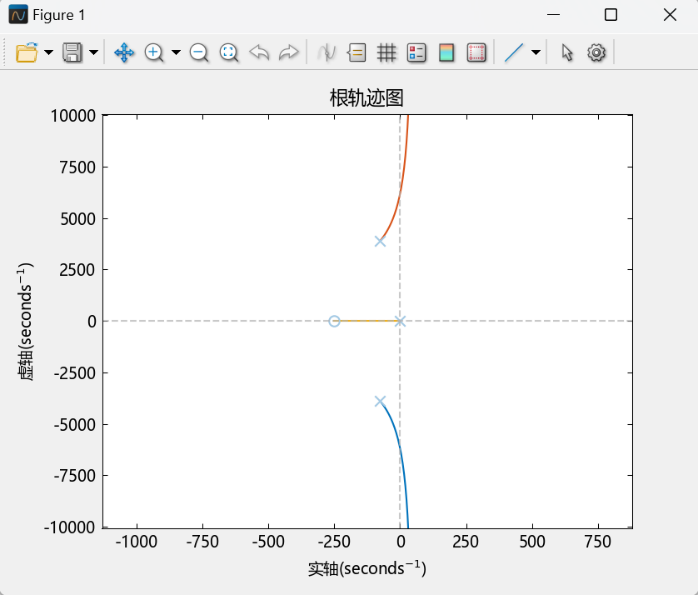
运行该段代码，得到MWorks绘制的根轨迹图如下：
根轨迹本质上反映的随着比例系数K_p的变化，特征方程根的变化情况；当两个共轭根恰好位于虚轴上时，此时对应的比例系数K_p（可将此时特征根带回特征方程求出）即为其稳定的边界值（大于该值不稳定，小于该值稳定）。
编写如下MWorks程序，寻找根轨迹与虚轴的交点并带回特征方程，求出比例系数K_p稳定边界值：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 % 找寻与虚轴交点 k = linspace(0 , 10 , 1000 ); % 增加点数，1000 个点 [r, k]=rlocus(G,k); real_part = real(r); imag_part = imag(r); % 查找实部接近零的索引 tolerance = 1e-1 ; % 设定阈值 idx = find(abs(real_part) < tolerance); % 找到所有交点的索引 intersections = r(idx); % 交点的复数值 % 求解临界kp s = intersections(2 ); % 系统参数 tao = 0.004 ; vm = 0.5 ; l = 10 ^(-4 ); c = 6.6 *10 ^(-4 ); vin = 15 ; r = 10 ; syms kp; % 定义符号变量 eq = tao*vm*l*c*s*s*s + tao*vm*l*s*s/r + vin*kp*tao*s + vm*tao*s + vin*kp == 0 ; solutions = solve(eq, kp); % 求解 real_solutions = real(solutions); % 取实部 decimal_solutions = double(real_solutions); % 转换为小数 disp(decimal_solutions); % 显示结果
运行上述MWorks代码，得到的比例系数K_p稳定边界值结果为：0.0514，这与先前依据劳斯判据得到的结果
而在实际情况下，需要考虑电容的寄生电阻；基于4.1节修正后的开环传递函数，代入数值可得：
$$10^{- 5}s)}{s(6.6 10^{- 8}s^{2} + 10^{- 5}s + 1)}
具有2个零点：
根轨迹的渐近线与实轴的夹角
编写MWorks代码如下：
1 2 3 4 5 6 using TyControlSystemss=tf('s' ); c = 6.6 *10 ^(-4 ); esr = 0.107185 ; G=(s+250 )*(1 +c*esr*s)/(s*(6.6 *10 ^(-8 )*s*s+10 ^(-5 )*s+1 )); rlocus(G);
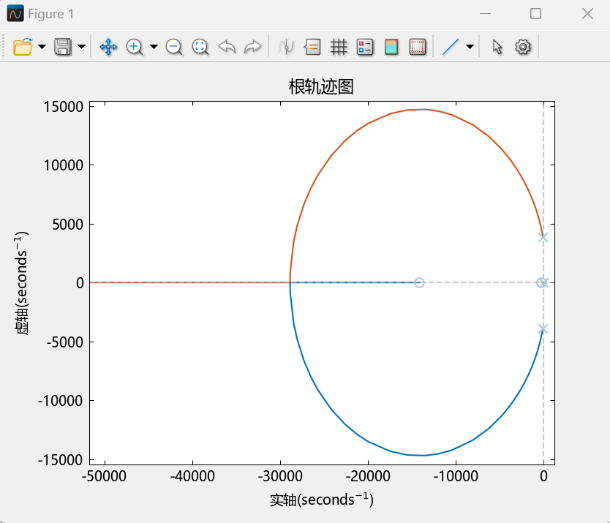
运行该段代码，得到MWorks绘制的根轨迹图如下：
可以看到，在考虑电容寄生电阻的情况下，根轨迹完全位于虚轴左侧，这意味着无论比例系数K_p（>0）如何变化，系统特征方程的根均位于虚轴左侧，即此情况下系统始终稳定，这与先前依据劳斯判据得到的结果也是一致的。这样的结果也充分说明，寄生电阻的加入使得系统的稳定性提高。
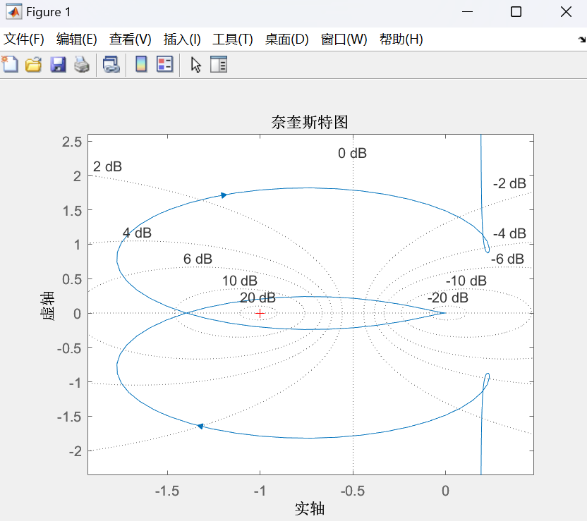
4.3 直流Buck变换器奈奎斯特稳定判据分析 在不考虑寄生电阻的情况下，基于3.1节得到的开环传递函数，取负载电阻R = 2欧姆，代入PI控制器参数：
$$
1 2 3 using TyControlSystemsH = tf([2.5 *10 ^7 2.5 *10 ^7 *5000 ],[6.6 5000 10 ^8 0 ]); nyquist(H);
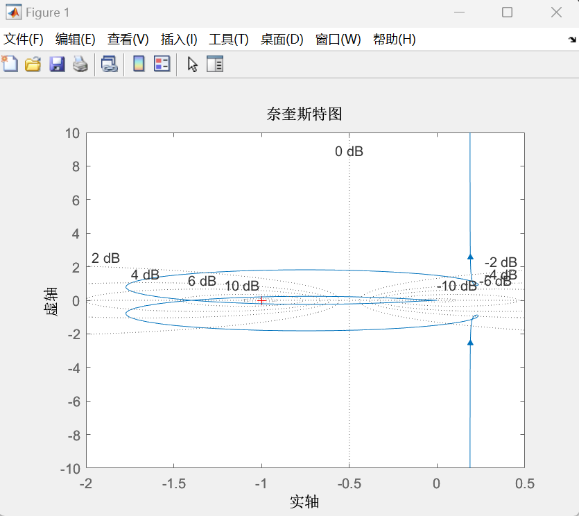
运行该段代码，得到MWorks绘制的奈氏图如下：
观察奈氏图图像可得：正穿越次数N+=1，负穿越次数N- =1
又由系统开环传递函数可知：系统开环右极点数P=0
故由奈奎斯特稳定判据可知：该闭环系统稳定。
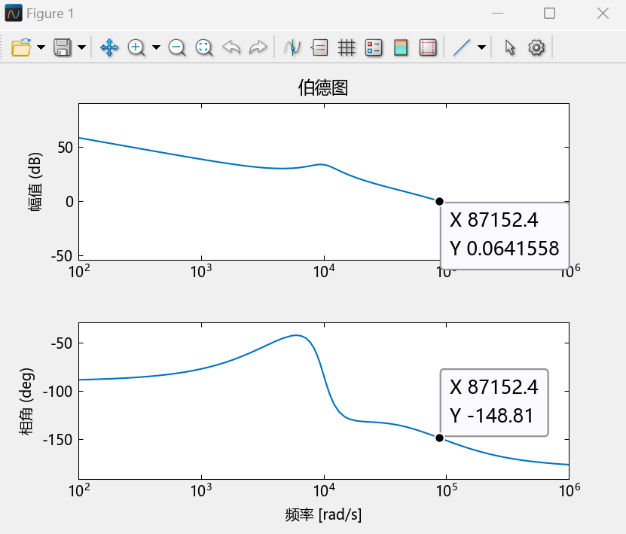
4.4 直流Buck变换器系统波特图分析（MWorks绘制） 与4.3节使用相同参数，即开环传递函数可写为：
$$
1 2 3 4 using TyControlSystemss=tf('s' ); G=2.5 *10 ^7 *(s+5000 )/(s*(6.6 *s^2 +5000 *s+10 ^8 )); bode(G);
运行该段代码，得到MWorks绘制的波特图如下：
从图中可读出：剪切频率
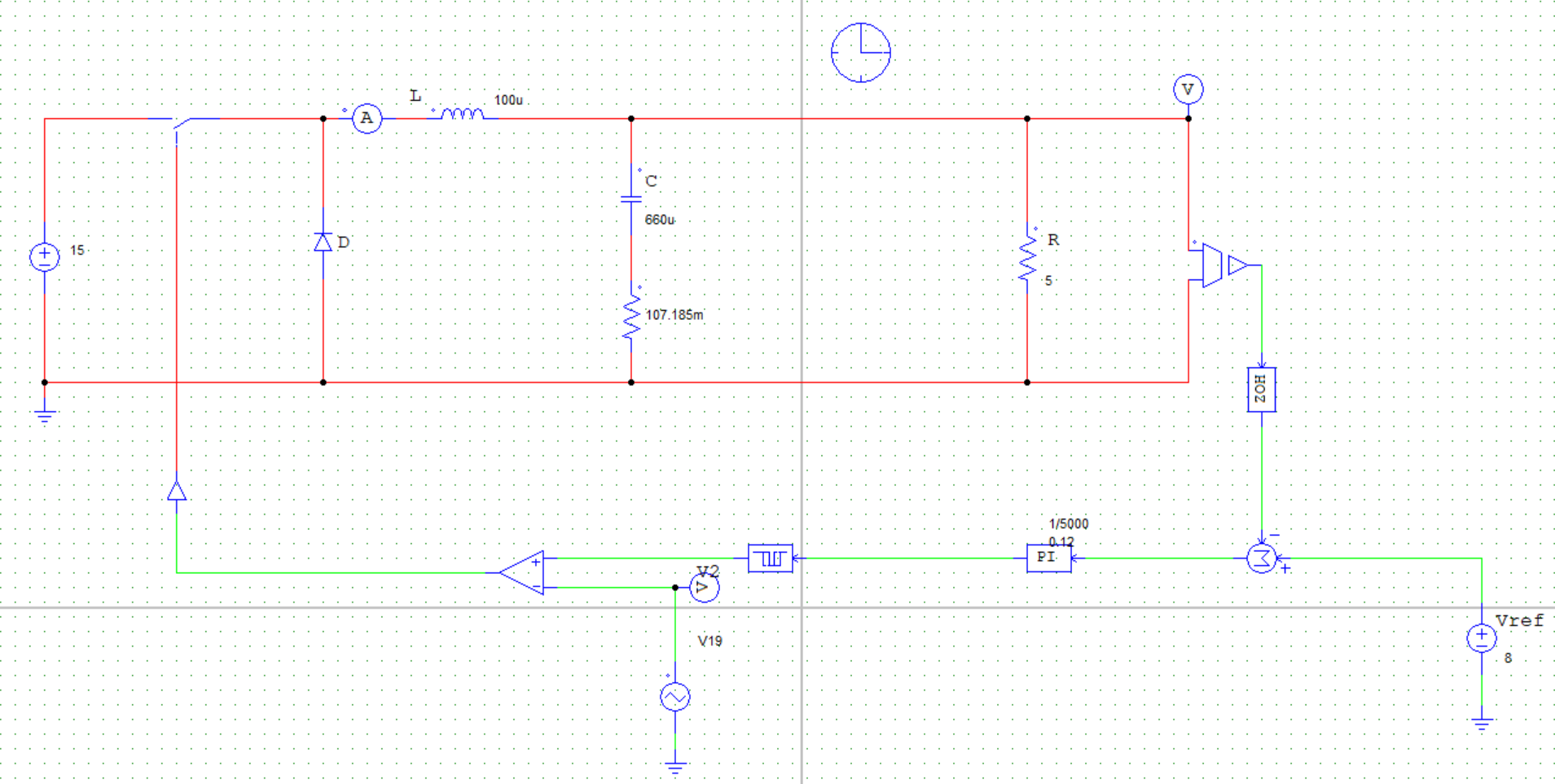
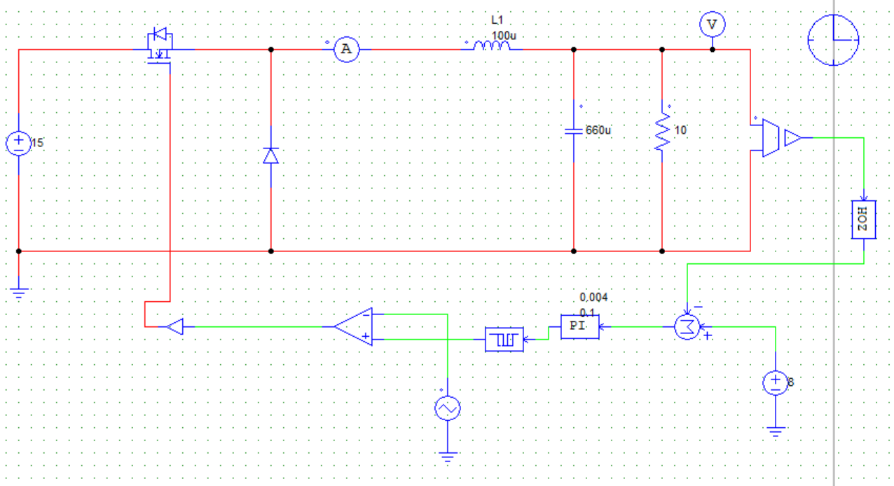
4.5 直流Buck变换器闭环负载稳定边界计算及仿真验证 基于2.2节中的电路元件参数以及输入电压恒为15V的客观事实，在给定PI控制器参数:
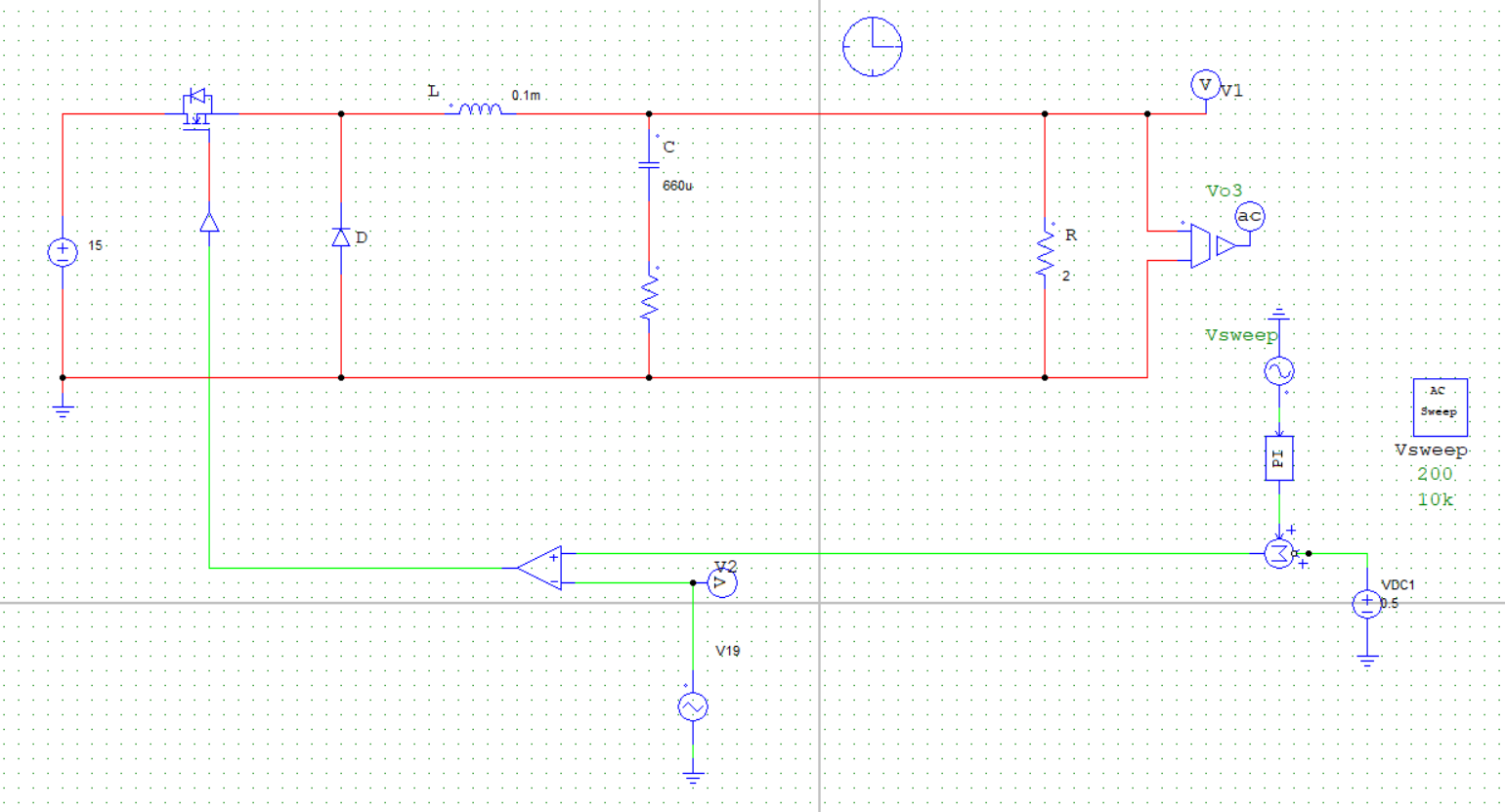
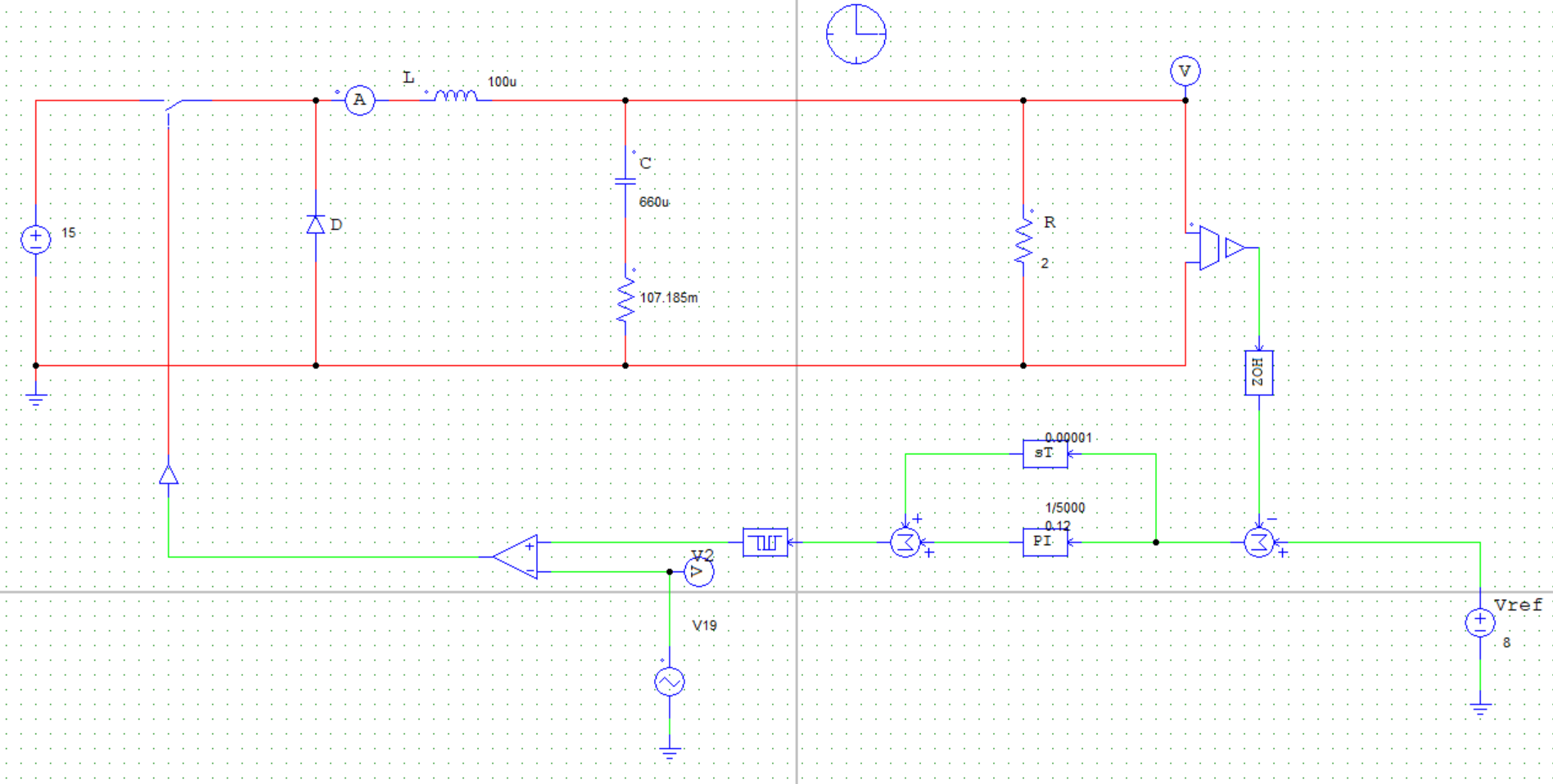
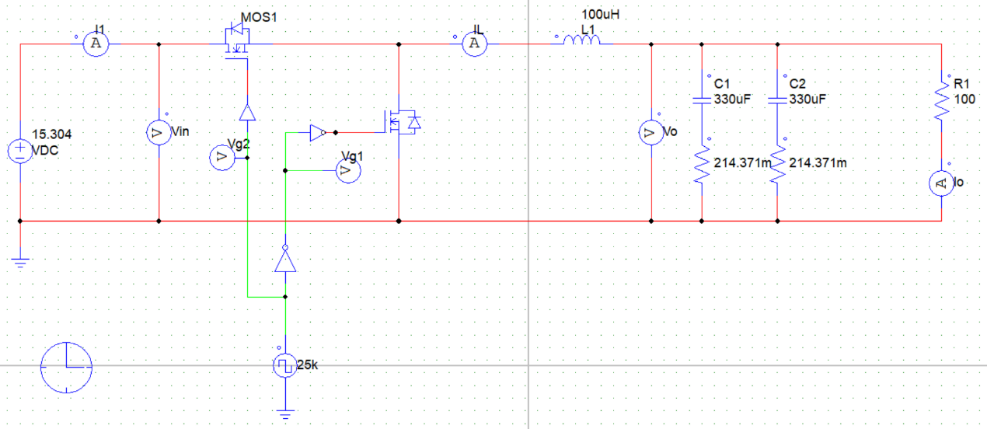
为进一步通过仿真验证计算结果，建立PSIM仿真电路图如下：
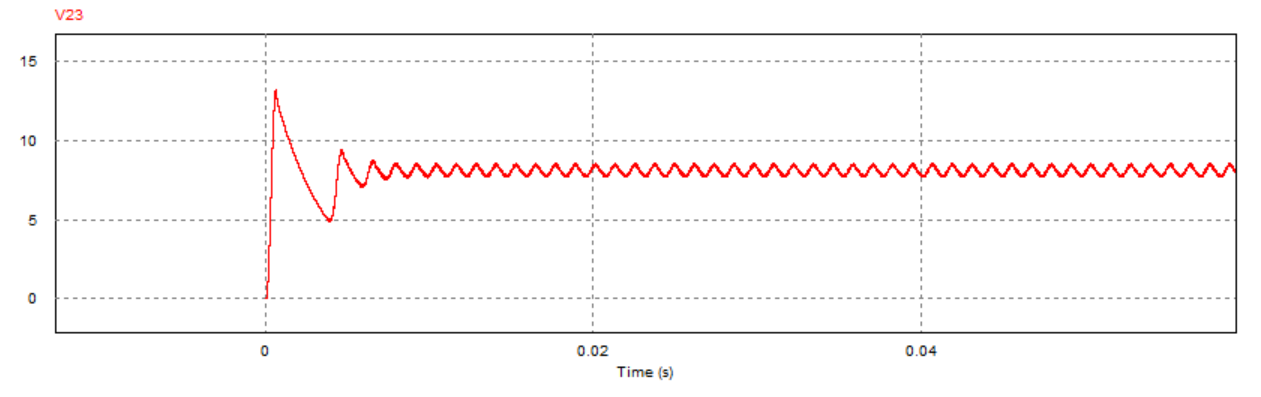
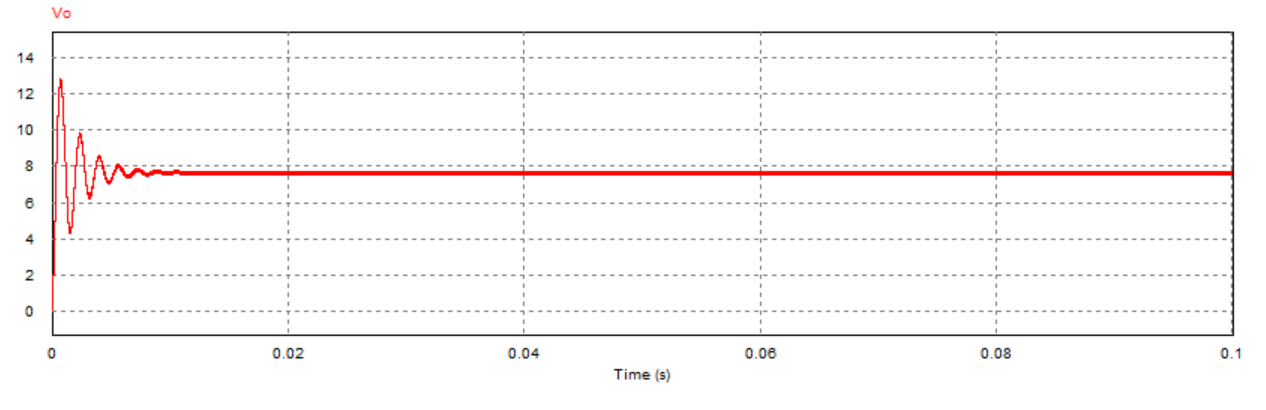
取负载电阻值R = 5Ω（小于临界值）时：
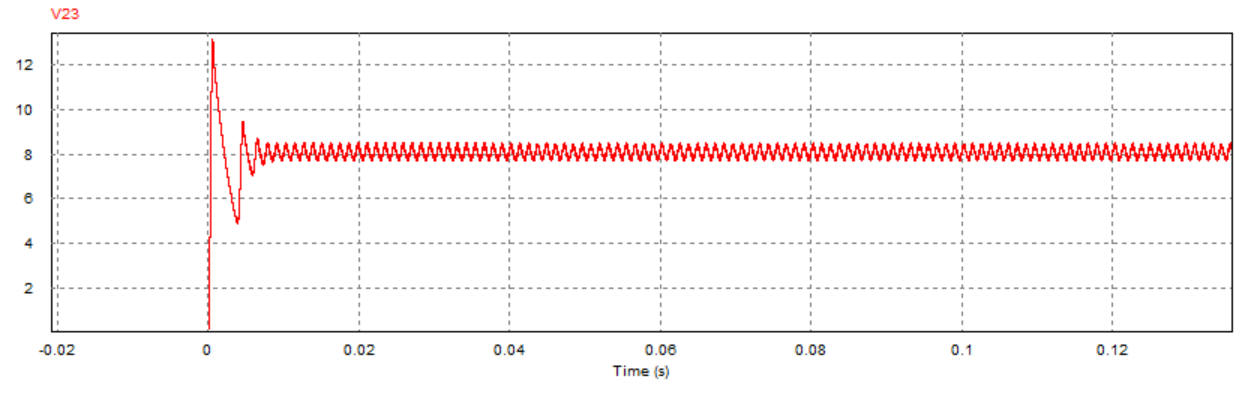
取负载电阻值R = 8.1欧姆（约等于临界值）时：
通过对比三组仿真结果可以发现：取不同的负载电阻值并不会影响系统的响应速度与响应瞬时超调量，而是影响输出电压趋于稳定后的纹波波形：
当负载电阻值小于临界值时，稳定后的输出电压会有较大的震荡（负载越小，震荡幅度越大），但该震荡上没有纹波，系统处于稳定状态；
当负载电阻接近临界值（实际临界值略小于8.1Ω）时，稳定后输出电压的震荡幅度减小，但开始出现纹波，系统处于临界稳定状态；
当负载电阻大于临界值时，稳定后输出电压的震荡幅度进一步减小，但纹波幅度有所增大，系统处于不稳定状态。
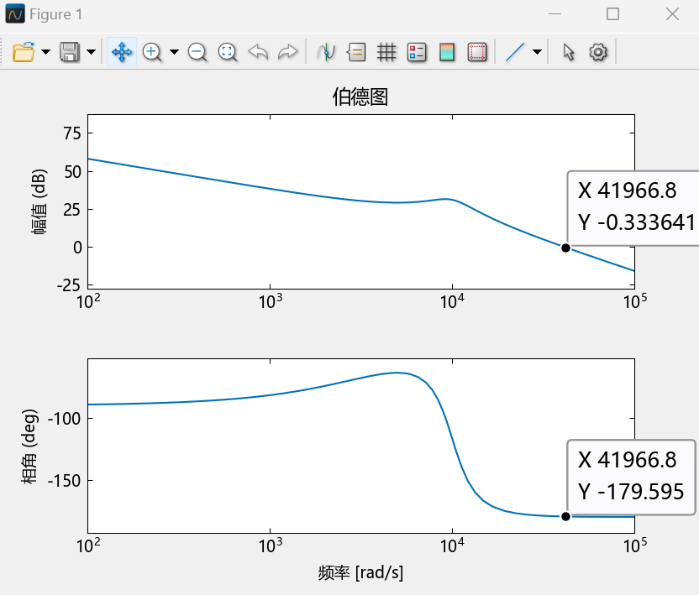
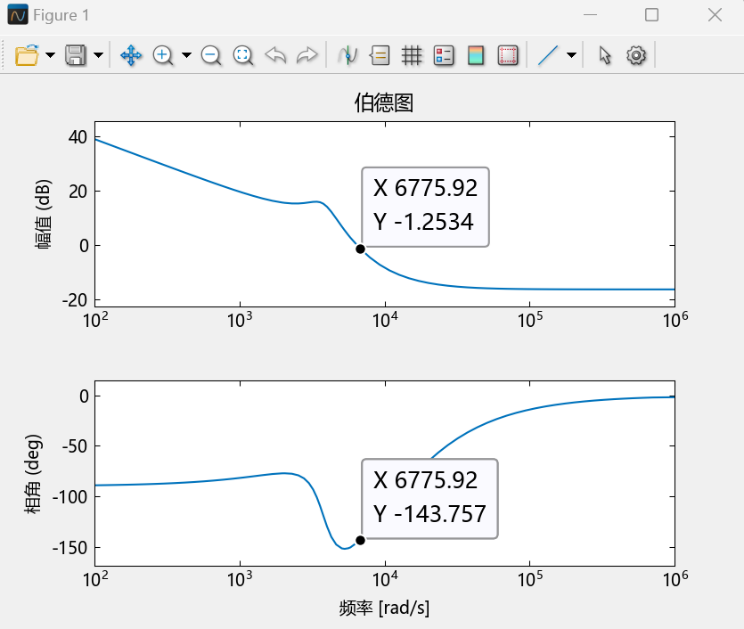
4.6 考虑寄生参数直流Buck变换器波特图分析（MWorks绘制） 在实际情况下，为实现对直流Buck变换器闭环控制系统更加精准的建模，需要考虑电容的寄生电阻，基于4.1节修正后的开环传递函数（取未近似结果）：
$$
1 2 3 4 5 6 7 8 9 10 11 12 using TyControlSystemss=tf('s' ); vm=2 ; r=2 ; esr=0.107185 ; c=6.6 \*10 \^(-4 ); l=10 \^(-4 ); vg=15 ; kp=1 ; tao=0.01 ; G=kp\*(tao\*s+1 )\*(esr\*c\*s+1 )\*vg/(tao\*s\*vm\*(l\*c\*(1 +esr/r)\*s\*s+(l/r+esr\*c)\*s+1 )); bode(G);
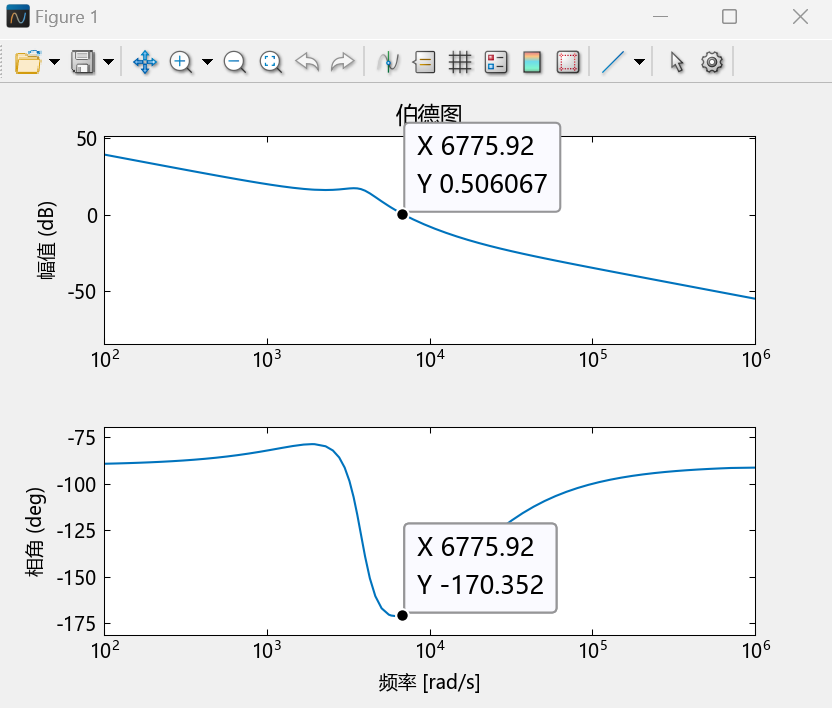
运行该段代码后绘制出的波特图如下：
从图中可读出：剪切频率
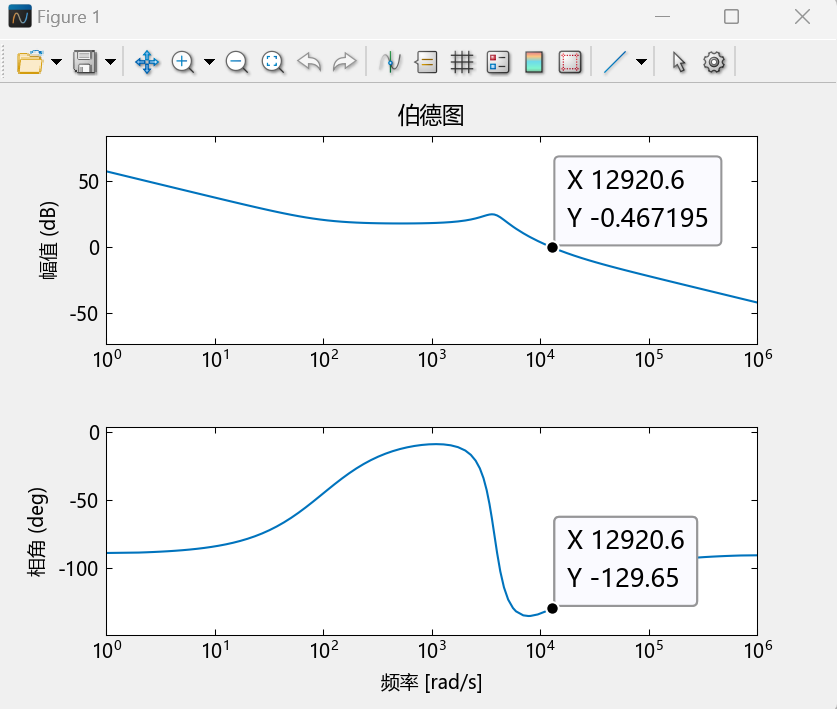
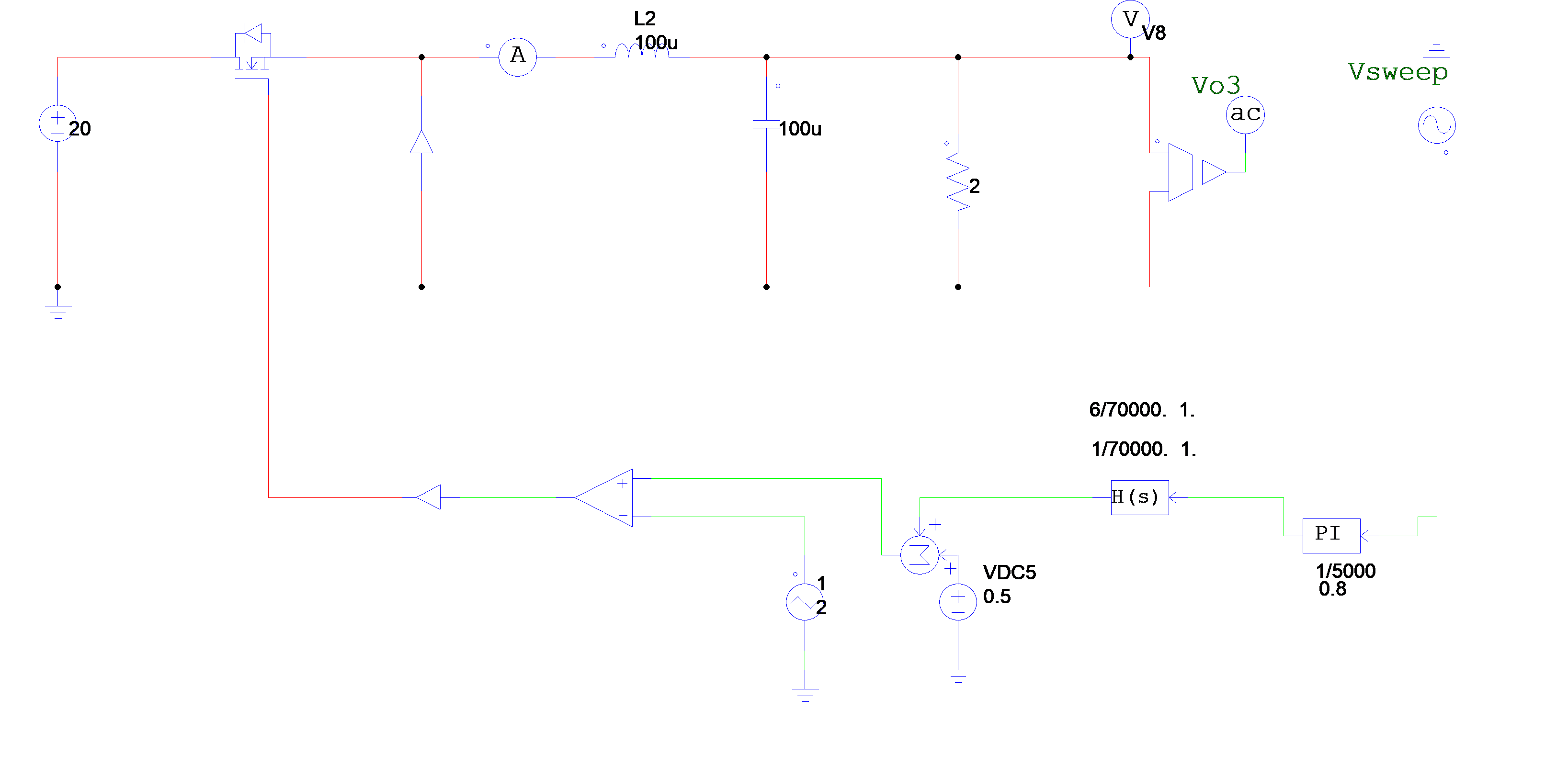
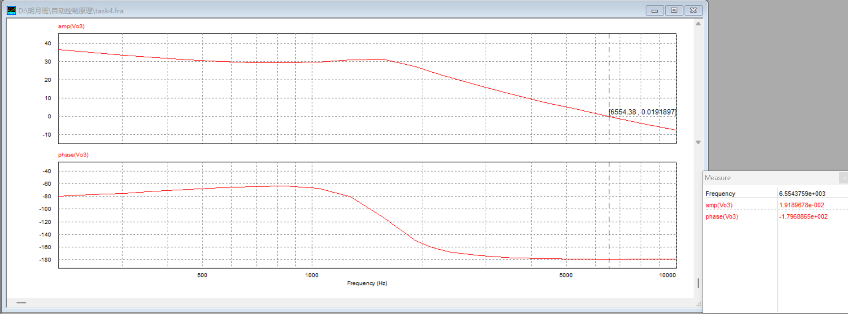
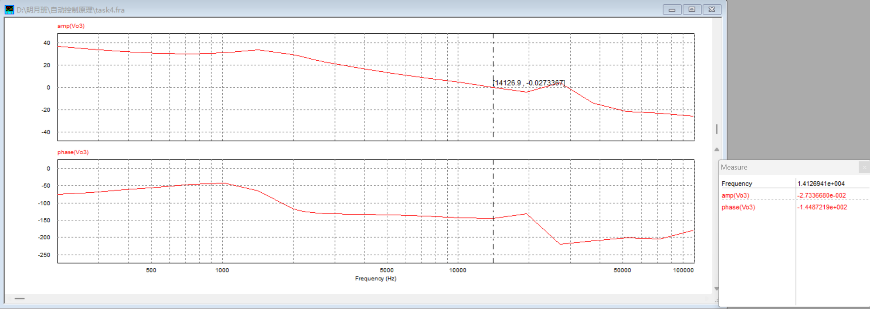
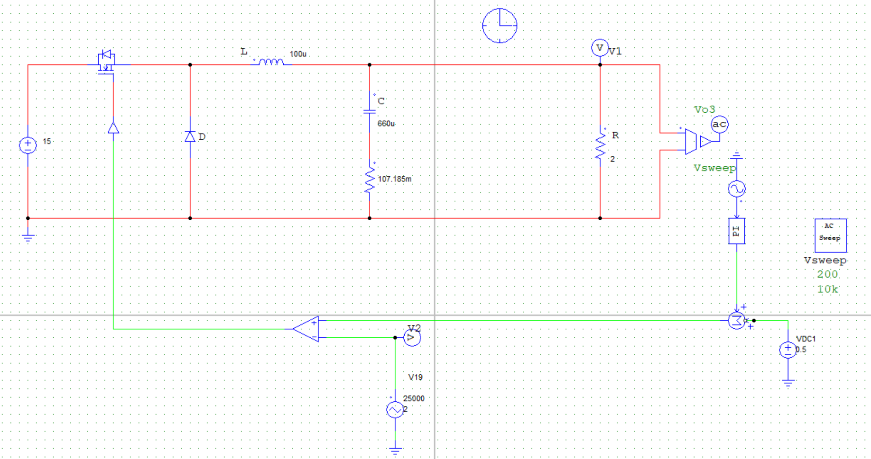
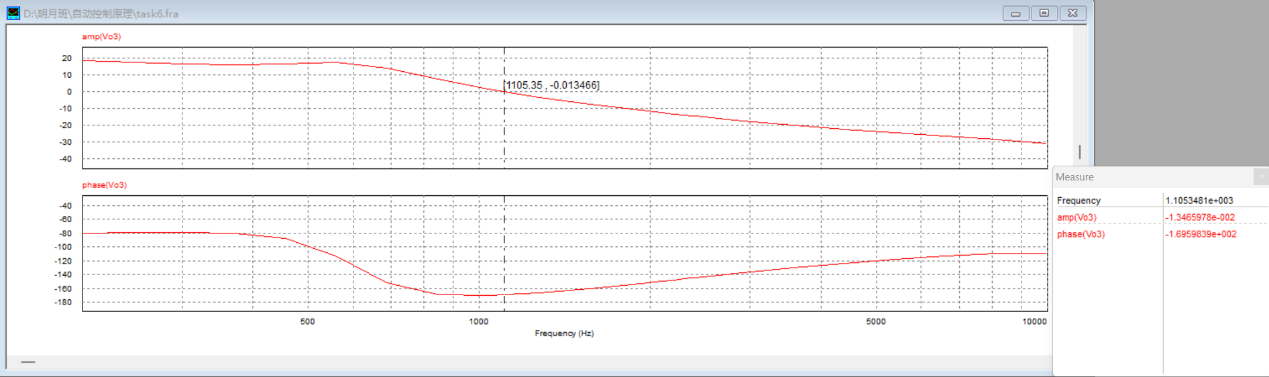
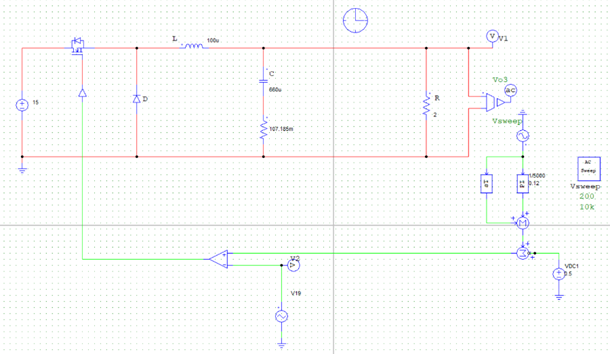
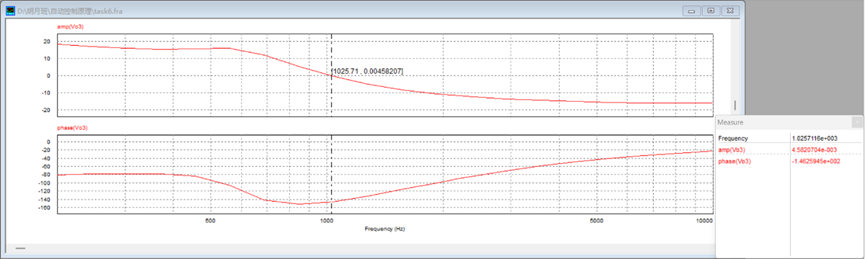
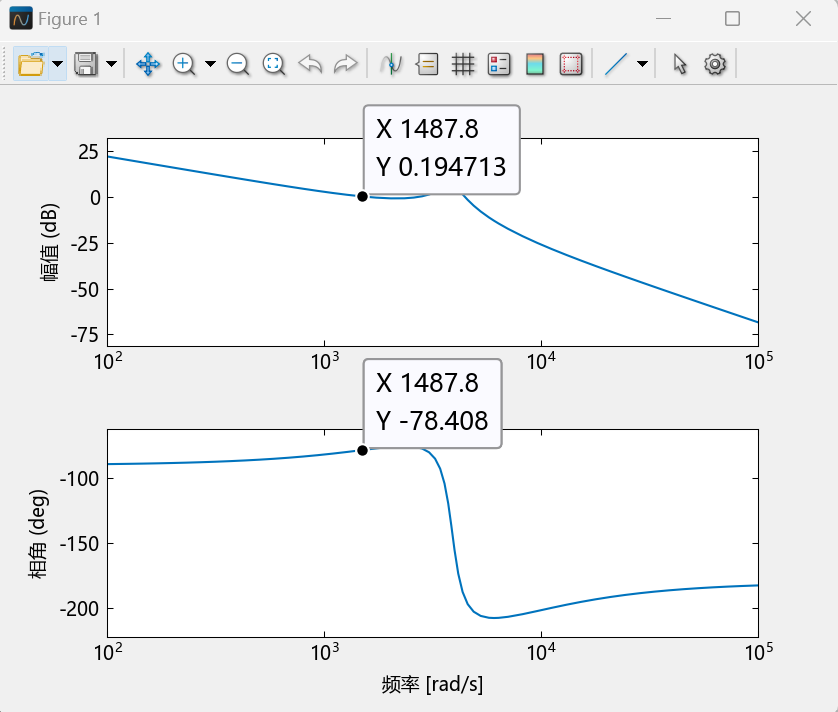
4.7 PSIM仿真扫频波特图 取与4.6节相同的参数，利用PSIM搭建扫频电路进行仿真得到波特图：
从图中可读出：剪切频率
若在仿真电路图中加入锁存器与零阶保持器：
图4.19：考虑寄生电阻——加入锁存器与零阶保持器后PSIM扫频仿真结果
从图中可读出：剪切频率
4.8 本章小结 本章主要对于直流Buck变换器闭环控制系统的控制性能进行了详细的分析，特别是针对系统的稳定性问题，从系统的开环传递函数入手，对于考虑电容寄生电阻与否的两种不同情况，在时域上利用劳斯稳定判据与根轨迹法，讨论在负载电阻R与PI控制器时间常数τ给定的情况下，PI控制器比例系数K_p的稳定边界；在频域上依据奈奎斯特稳定判据（基于奈奎斯特图）与对数频率特性稳定判据（基于波特图，由MWorks绘制与PSIM扫频仿真得到，两者结果高度吻合），通过系统相位裕度γ判断闭环系统稳定性，同时在PI控制器参数给定的情况下讨论负载电阻R的稳定边界，并搭建PSIM仿真电路对不同负载电阻下闭环系统的稳定性进行验证，仿真结果与理论推导结论基本一致。
5 直流Buck变换器闭环控制实验 5.1 KEIL5软件环境安装及创建 Keil 5是一款集成开发环境（IDE），它以其强大的功能和丰富的特性，在嵌入式系统开发领域占据了重要的地位。在本项目中，需要借助该IDE编写主控代码并烧录至STM32芯片中，使其能够在闭环控制系统中正常发挥控制作用。
下载助教在课程群内上传的安装程序压缩包并解压，文件夹内包含如下文件：
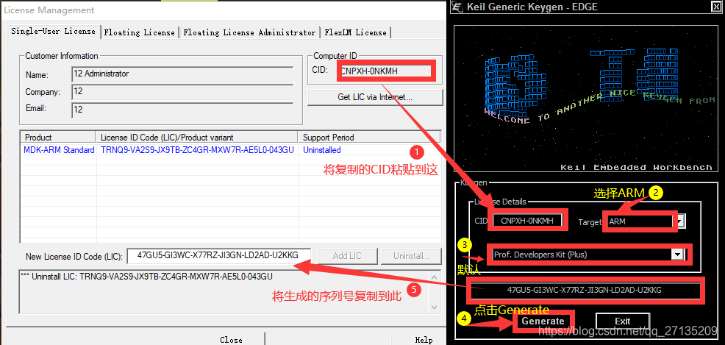
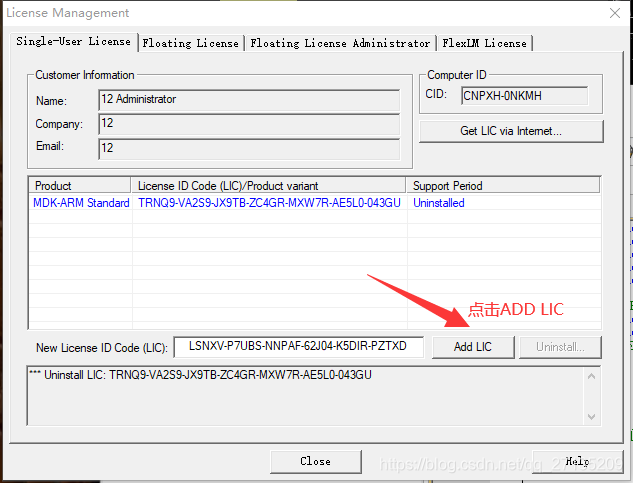
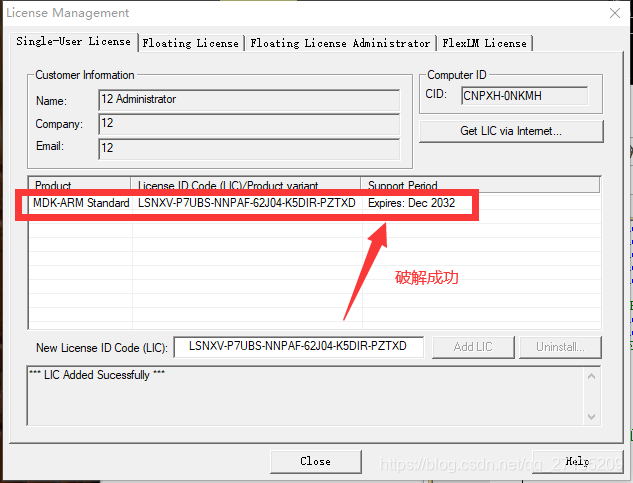
双击安装程序”MDK524a.EXE”，一路点击”NEXT>>“（注意勾选同意许可证条款与指定软件安装位置）即可完成Keil5软件安装；软件安装完成后会自动运行，关闭后需要重新以管理员身份运行Keil5（右键->以管理员身份运行），随后进入keygen_new2032文件夹，双击运行破解程序”keygen_new2032.exe”，输入Keil5软件内”File->Licence Management…”里的CID并选择ARM，点击”Generate”并将生成的序列号复制到Keil5软件内”File->Licence Management…”下方的LIC一栏，点击”ADD LIC”即可完成破解。
除此之外，针对本项目选用的STM32F103C8T6芯片，还需要安装相关芯片库：双击”支持包”文件夹中的”Keil.STM32F1xx_DFP.2.2.0.pack”文件并点击”NEXT>>“即可完成安装。
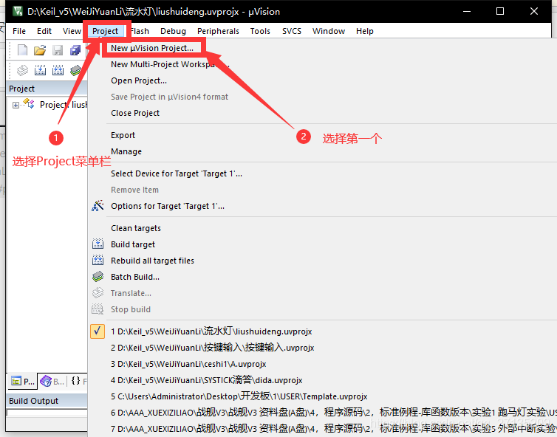
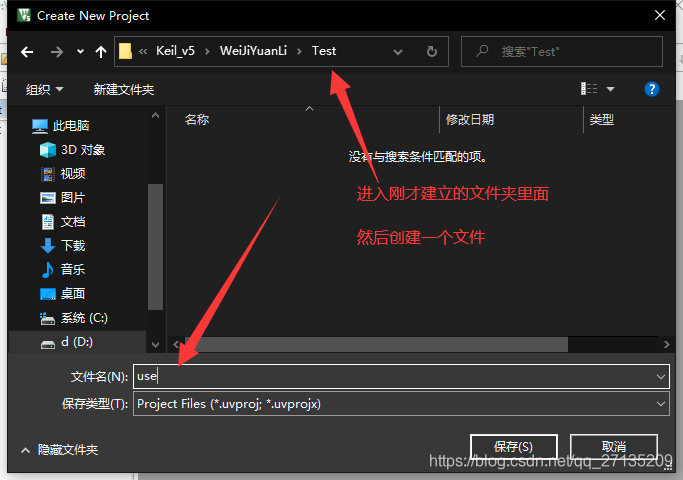
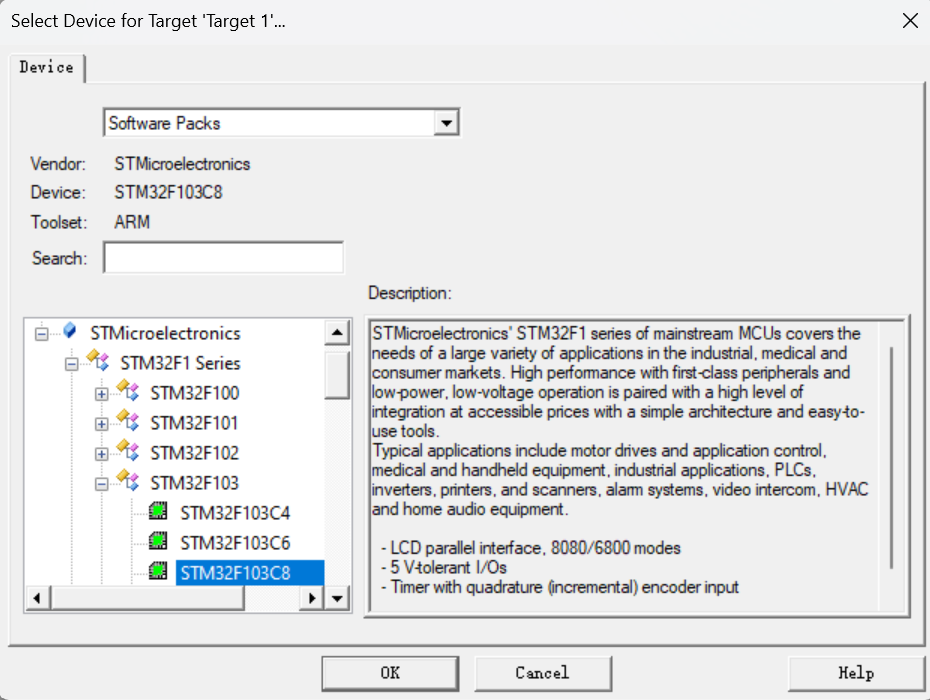
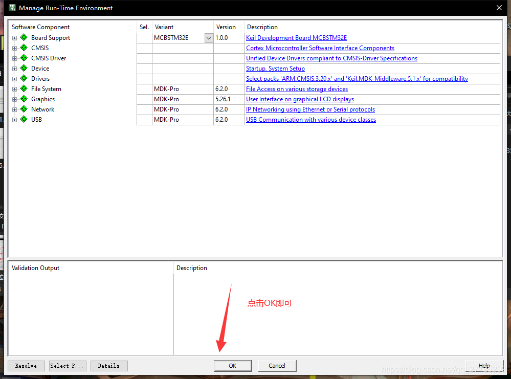
完成软件环境的安装后，需要进入Keil5软件，点击上侧菜单栏中”Project->New μVision Project”新建工程，随后会进入到芯片设备的选择环节，选择芯片”STM32F103C8”并点击”OK”，在弹出的Manage Run-Time Environment对话框中再次点击”OK”即可完成工程创建。
当然事实上这样建立的工程仍然无法正常使用，还需要引入一系列启动文件与库函数文件等，具体流程在此不详细赘述，可以参考博客：如何在keil中建立一个STM32F10x完整工程 。至此Keil5的软件环境安装及工程创建过程已经全部完成，再额外导入一些系统辅助函数文件（如”Delay.c”等），即可在”main.c”文件中进行闭环控制程序的编写了。
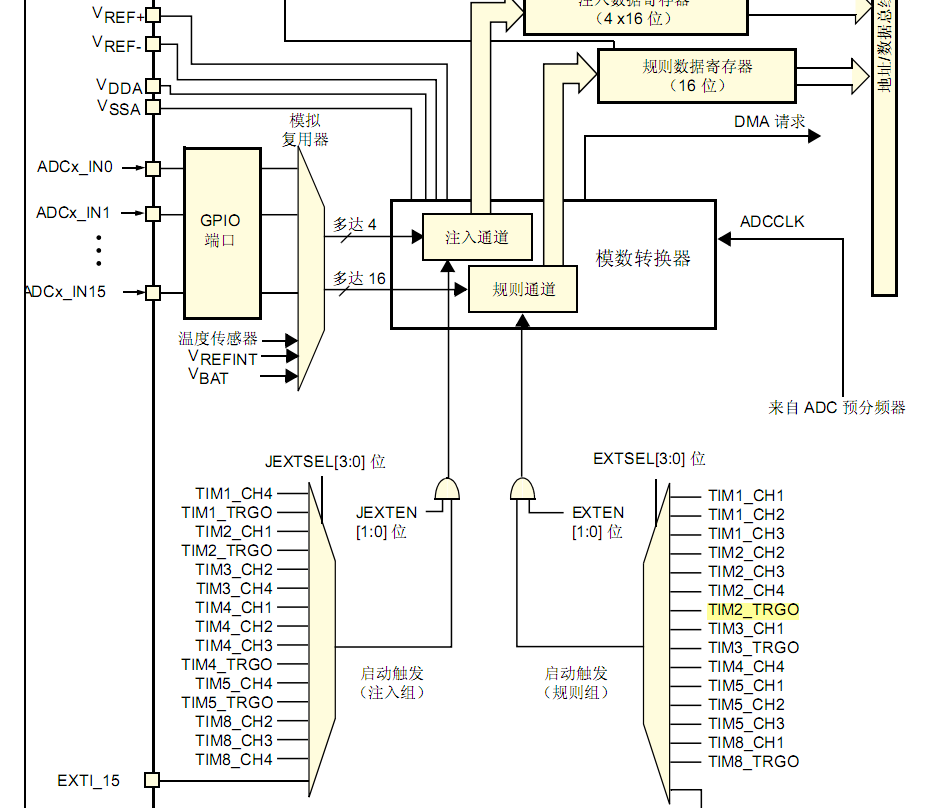
5.2 ADC采样及PWM生成原理 ADC（Analog-to-Digital Converter），即模拟到数字转换器，主要用于将连续传输的模拟信号转换为数字信号，便于数字系统（如中央处理器CPU、微控制器MCU等）对传输信息进行快速处理和分析。
采样是指ADC在一定时间间隔内对连续变化的模拟信号进行取样，得到一系列离散的样本点，实现在有限采样率条件下，无失真还原信号波形信息。采样率决定了每秒采集的样本量，通常单位为Hz；其必须满足奈奎斯特采样定理（大于信号最高频率的两倍），否则会产生混叠。
由于数字信号本身不具有实际意义，仅仅表示一个相对大小，故任何一个模数转换器都需要一个参考模拟量作为转换的标准，比较常见的参考标准为最大的可转换信号大小，而输出的数字量则表示输入信号相对于参考信号的大小。在STM32单片机中，ADC为12位，即单片机读取的ADC值应在0~4095范围内，这样的ADC值与0~3.3V的输入电压值之间存在线性对应关系（若输入电压范围超出0~3.3V，则需要在输入ADC引脚前加入电阻分压和放大器等外围电路，在2.3.4小节中有详细介绍该部分采样电路）。
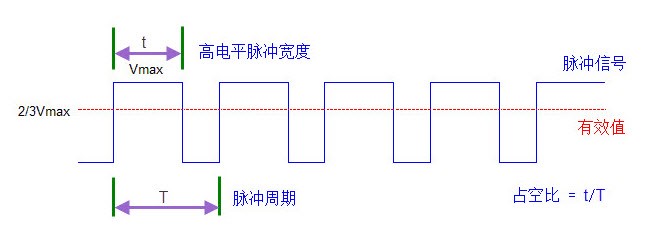
PWM（Pulse Width Modulation），即脉冲宽度调制，是一种通过调节脉冲信号的宽度（即占空比，高电平持续时间占整个周期的比例）来控制输出信号平均值的方法。在具有惯性的系统中，可以通过对一系列脉冲的宽度进行调制，来等效地获得所需要的模拟参量。简单而言，PWM可以视为一种DA（数字->模拟）转换，通过产生PWM波形这一数字信号等效地实现了模拟信号的输出。
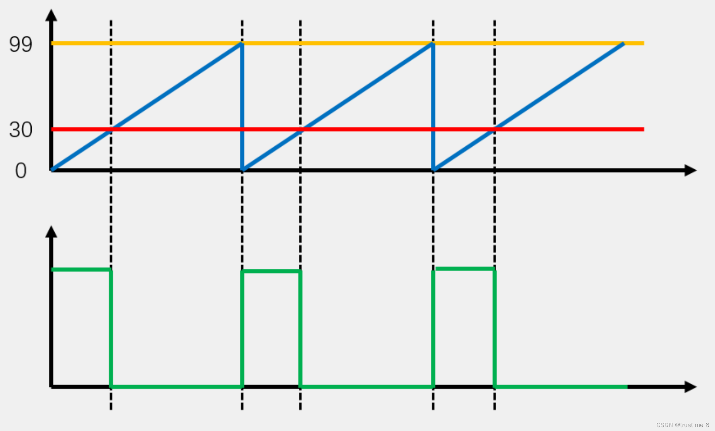
PWM实现的原理是：通过锯齿波/三角波(载波)所需要合成的波形（调制波）进行比较，然后确定PWM所需要输出的极性，锯齿波从比较器的反相端端输入，当大于参考电压时输出与锯齿波相反的极性，而当锯齿波从比较器同相端输入，当大于参考电压时输出与锯齿波相同极性。
在Keil工程中，基于以上PWM生成原理编写函数文件”PWM.c”，其中包含了生成PWM波形所需的全部函数。实际运行时，PWM波形是通过定时器的计数和输出比较模块的配合生成的，其具体过程如下：
（1）计数器计数：TIM2定时器按照内部时钟驱动，从0计数到ARR（2999），然后重新清零，重复循环。
（2）比较与输出：定时器每次计数到CCR（1500）时，切换PWM输出的电平状态：从计数开始到计数器值为CCR时，输出高电平；从计数器值为CCR到ARR，输出低电平。
（3）占空比：由CCR与ARR的比值决定。程序中初始设定CCR=1500，ARR=2999，故可计算得出占空比为
5.3 基本PI控制理论及程序 PI控制器是比例-积分控制器的一种，其核心是通过调节控制变量（输出电压），使系统输出接近目标值，是在控制工程中技术成熟、理论完善、应用最为广泛的一种控制策略。
对于PI控制器而言，其控制量的计算公式为：
（1）e(t)：当前时刻系统输出电压与参考电压之间的误差值；
（2）K_P：比例增益系数，用于快速响应；
（3）K_I：积分增益系数，用于消除稳态误差；
（4）u(t)：待控制变量——系统输出电压。
写成微分方程形式则为：
$$
从时域上看，只要存在偏差，积分就会不停对偏差积累，因此稳态时误差一定为零；
比例与积分动作都是对过去控制误差进行操作，不对未来控制误差进行预测，限制了控制性能；
PI调节将比例调节的快速反应与积分调节消除静差的特点结合，主要用于改善控制系统的稳态性能。
在Keil工程中的主函数文件”main.c”中，其main函数在进行了PWM、ADC与串口等必要的初始化后，在while循环中反复运行update_voltage_reference与control_buck两个函数，其中前者主要是进行参考电压的动态更新，而后者中则包含了PI控制的主要逻辑，部分核心代码如下：
1 2 3 4 error = voltage_ref \* 2500 \* 1000 / 1050 / 20000 - voltage_fb; integral += error; control_signal = KP \* error + KI \* integral; last_error = error;
该段代码主要按照如下流程实现PI控制：
误差计算：error
其中V_ref（voltage_ref）为函数update_voltage_reference中设定的目标电压，而V_fb（voltage_fb）为系统输出并反馈至控制器的实际电压。
积分计算：
PI控制量：control_signal
除此之外，为防止占空比超出合理范围，还对控制信号control_signal进行约束：
1 2 3 4 if (control_signal \> 0.8 ) control_signal = 0.8 ; else if (control_signal \< 0.2 ) control_signal = 0.2 ;
除了PI控制的核心逻辑外，在主控函数control_buck中还实现了其他功能：
模拟信号采集得到系统输出并反馈至控制器的实际电压V_fb（voltage_fb）：
1 2 voltage_fb = (float )AD_GetValue()\*3.3 /4096 ; trueVoltage = voltage_fb \* 1050 \* 20000 / 2500 / 1000 ;
根据PI控制结果，实时更新PWM占空比：
1 2 3 duty_cycle = control_signal \* PWM_PERIOD; i = (int )duty_cycle; PWM_SetCompare1(i);
通过串口发送调试信息，用于监控采样值和控制效果：
1 Serial_Printf(\"%d,%.2f\\r\\n\", sample_index, trueVoltage);
5.4 闭环PI稳压调控输出（8V、10V） 5.3节中对于主控函数control_buck进行了详细的解析，整个闭环PI调控过程都由此函数完成，在此不重复赘述；而对于函数update_voltage_reference而言，该函数实现了电压的切换：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void update_voltage_reference (void ) { time_counter += 40 ; if (time_counter \>= 10000 ) time_counter = 0 ; if (voltage_state == 0 ){ voltage_ref = 10.0 ; voltage_state = 1 ; } else { voltage_ref = 8.0 ; voltage_state = 0 ; } } }
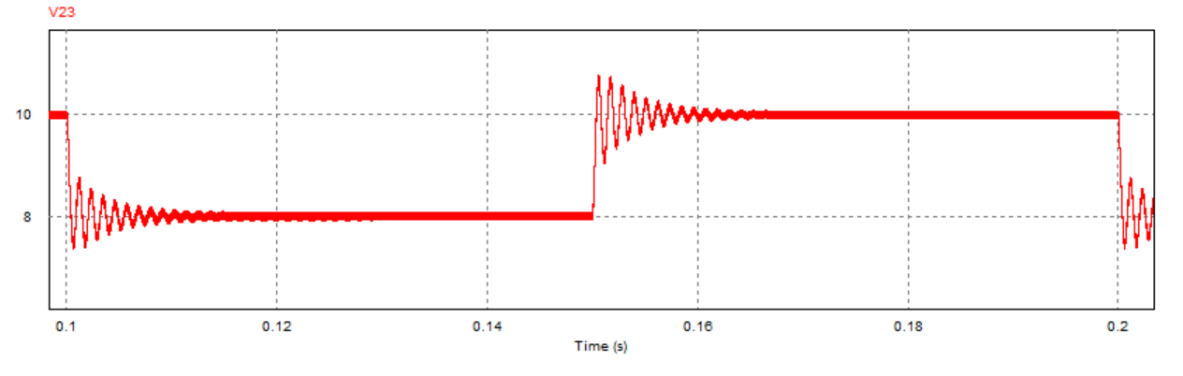
可以看到，该函数每隔10秒就对于目标电压voltage_ref进行一次切换，由10V切换为8V，再由8V切换回10V，循环往复。该函数主要用于模拟动态负载或参考值变化的情景，以测试控制器再目标电压变化时的响应性能。
事实上，在main函数中，在进行各项初始化（PWM、ADC、串口等）后，while循环中只有参考电压切换函数update_voltage_reference与PI主控函数control_buck反复作用，也正是这两个函数使得该直流Buck变换器闭环控制PI系统能够交替稳压输出8V或10V的电压。
5.5 闭环参考电压8V-10V连续跳变实验与分析（仿真+实验） 在直流Buck变换器闭环PI控制系统参考电压8V-10V连续跳变实验时，重点对于输出电压分别为8V与10V的两种情况下单片机的PWM输出波形进行测试，通过观察其占空比反映其输出电压情况：
先使用仿真器给单片机供电，以调试PWM波形输出是否正常；
将上述闭环控制程序放入Keil工程中，成功编译后烧录至单片机内，将单片机（最小系统板）插入电路板上预留的引脚接口处并上电测试，使用示波器或者上位机观测电路板PA8端口输出PWM波形的占空比。
可以看到，在参考电压设置为8V时，单片机输出的PWM占空比明显小于参考电压为10V时的结果。
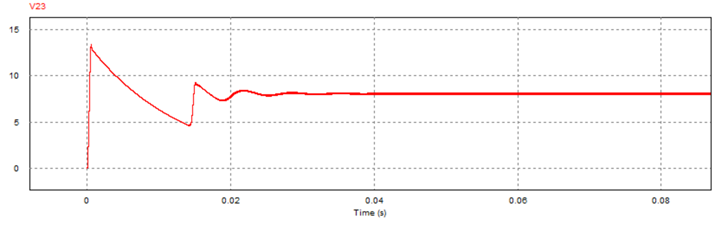
为进一步观察参考电压连续跳变时的动态响应过程，进行了对应的PSIM电路仿真（仿真参数：kp=0.12，τ_i=1/5000，R=2Ω），其中跳变效果通过在直流参考电压后接入一个周期方波信号实现，跳变周期为0.1s：
可以看到，跳变瞬间系统的动态响应较快（约为0.01s）且输出电压稳定后震荡幅度较小，说明该参数下系统具有较好的动态响应性能。
5.6 本章小结 本章主要介绍了对于直流Buck变换器PI闭环控制的整体实验流程，从STM32单片机编程环境的搭建，到根据PWM生成原理编写PWM的初始化函数及占空比实时调控函数，再到根据PI控制的基础理论编写对应的主控代码，在参考电压连续跳变（8V-10V）的情况下调控闭环PI的稳压输出，最后将代码烧录进行实际实验，测试单片机的PWM输出调控情况，并通过仿真观察参考电压连续跳变时的动态响应情况。通过该闭环控制实验，充分证明了PI闭环控制系统对于直流Buck变换器具有良好的控制效果。
6 复合PI控制直流Buck变换器 6.1 PI+超前校正（复合PI）分析设计 为提高PI闭环控制系统暂态响应速度，可以在原有的控制系统中加入一些其参数可以根据需要而改变的控制器，即对于系统进行校正，从而使整个系统的频率特性发生变化。本项目中针对直流Buck变换器的PI闭环控制系统，采用PI+串联超前校正的复合PI控制器，以进一步提升系统性能指标。
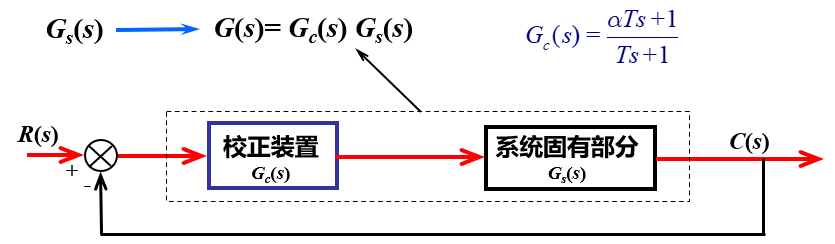
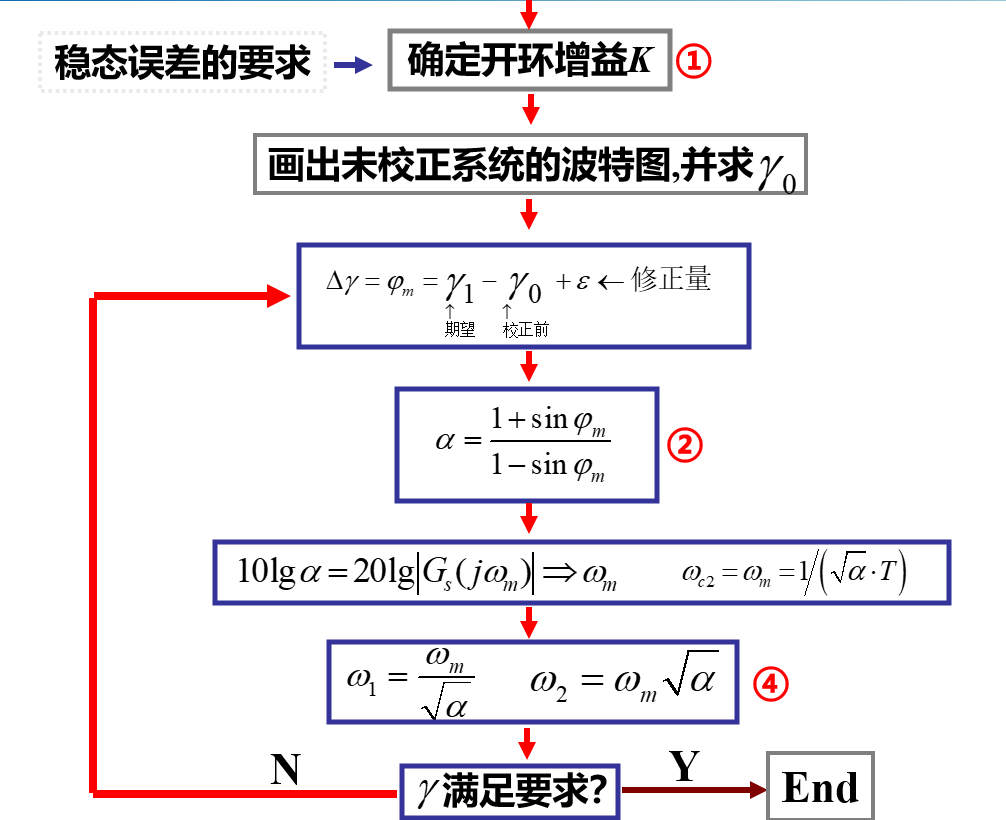
串联超前校正的核心思想是，将补偿中心ω_ m设计为期望剪切频率ω_ c处，从而提升剪切频率(补偿中心)所对应相位，并利用补偿处增益放大(+20)来改善剪切频率处斜率。具体的设计流程如下：
根据静态性能指标，确定开环增益K
为确定校正环节的设计方向，根据所确定的开环增益，画出系统固有部分G_s(s)的波特图，并计算其剪切频率ω_ c1与相位裕度γ_ 0；
根据要求的相位裕度γ，确定
由φ_m确定α：
令校正后剪切频率
画出校正后系统的波特图，并验算相位裕度是否满足要求：若满足要求，则需要在原有PI控制器前增加环节
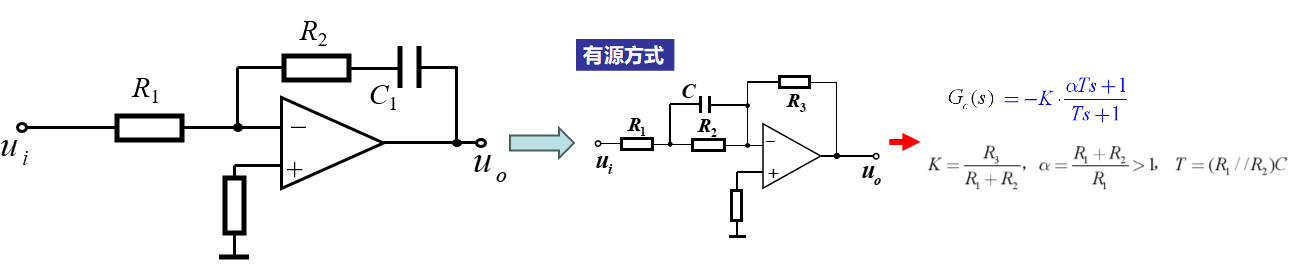
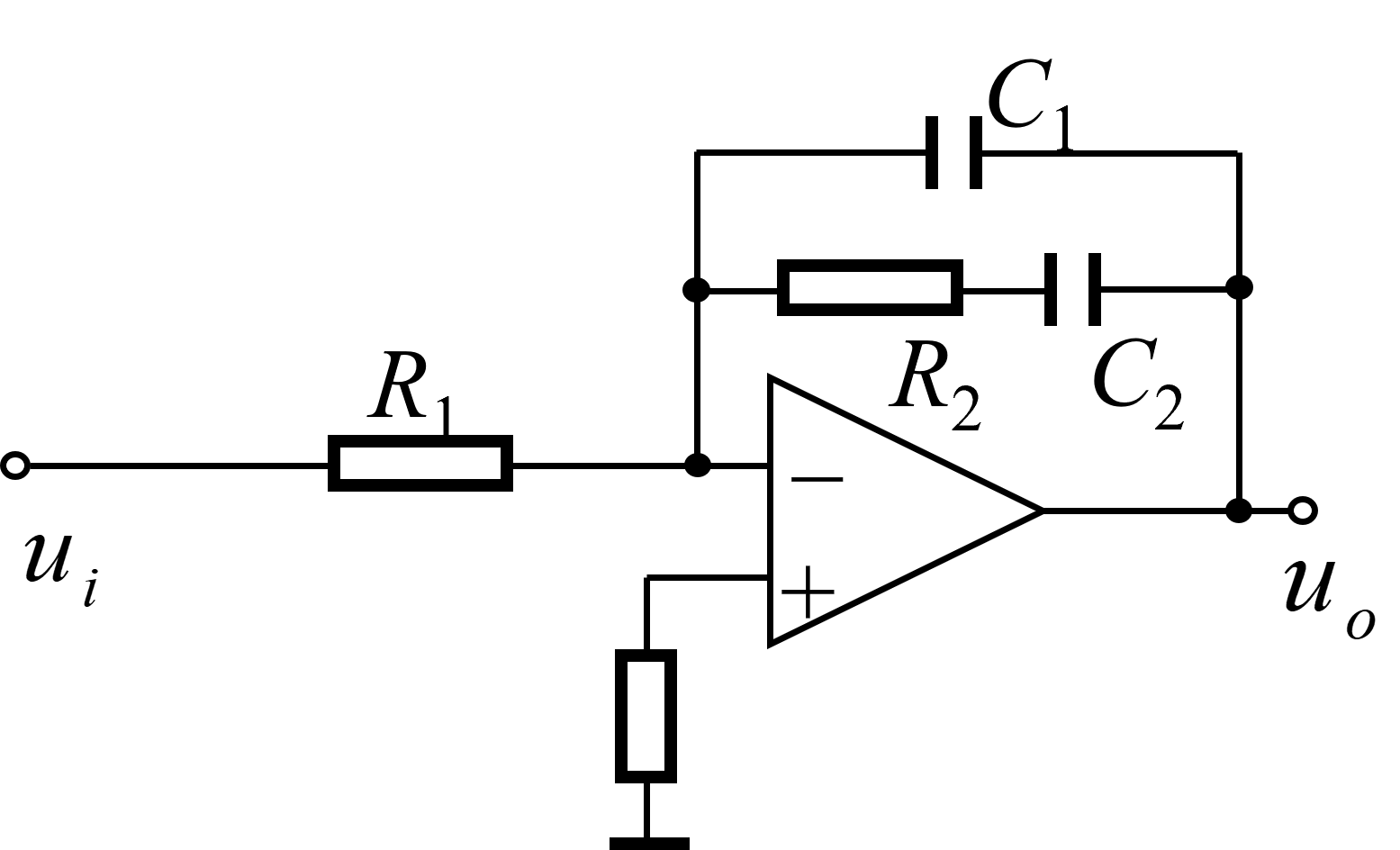
对于比例积分PI控制器，一般采用如下的超前校正方式：
图6.3：PI控制器超前校正电路原理图
针对直流Buck变换器的PI闭环控制系统，给定PI控制器参数:
1 2 3 4 5 6 7 8 9 10 11 using TyControlSystemss=tf('s' ); vm=1 ; r=2 ; c=10 ^(-4 ); l=10 ^(-4 ); vg=20 ; kp=0.8 ; tao=1 /5000 ; G=kp*(tao*s+1 )*vg/(tao*s*vm*(l*c*s*s+(l/r)*s+1 )); bode(G);
绘制出校正前的波特图：
从图中可读出：校正前系统的剪切频率
为使得校正后的相位裕度
$$
$$
1 2 3 H=(6 *s/70000 +1 )/(s/70000 +1 ); G1=G*H; bode(G1);
绘制出校正后的波特图：
从图中可读出：校正后系统的剪切频率
6.2 复合PI控制PSIM仿真（校正前后参考电压变化时输出电压分析） 首先通过PSIM扫频仿真对先前波特图的MWorks绘制结果进行验证：
从图中可读出：校正前系统的剪切频率
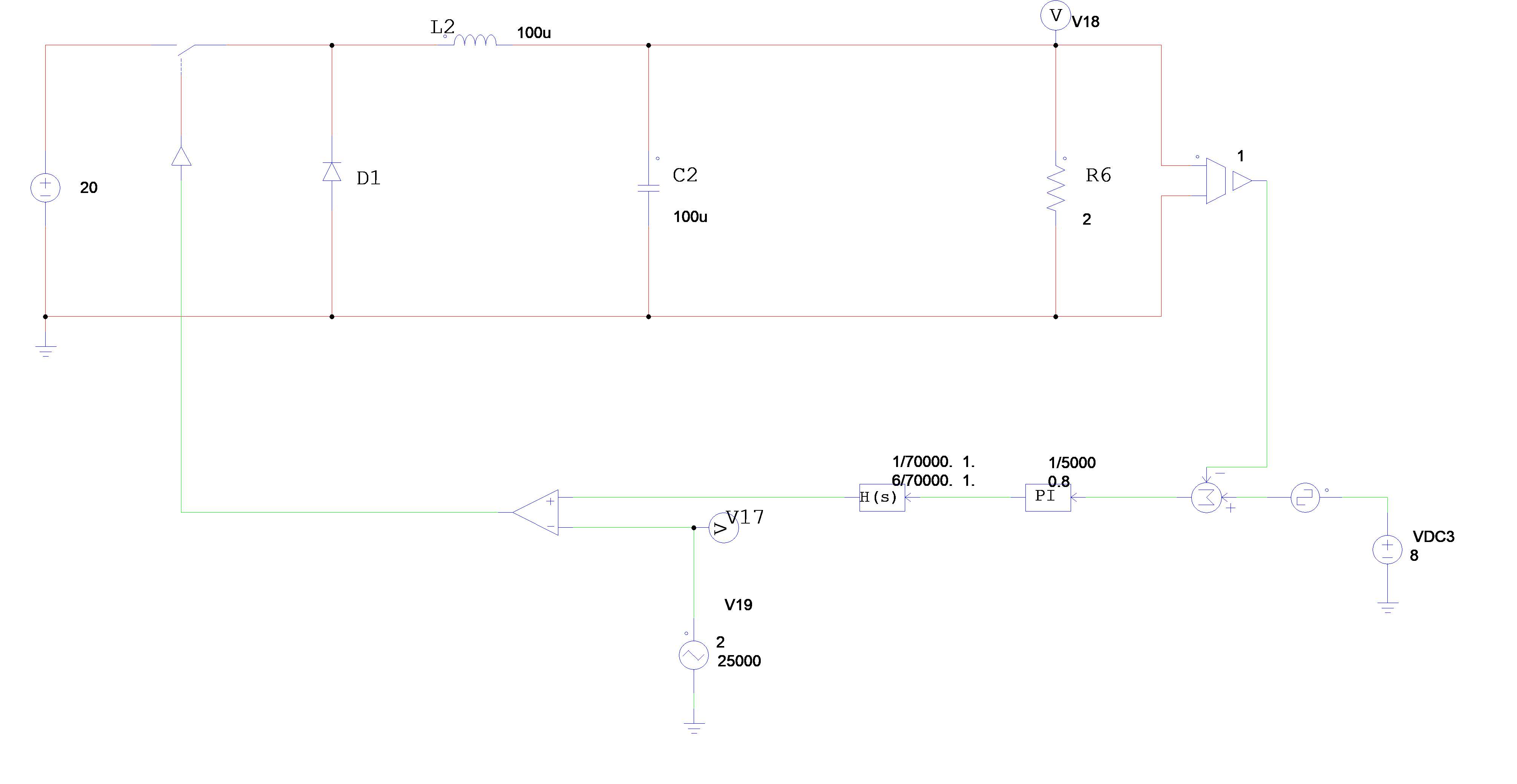
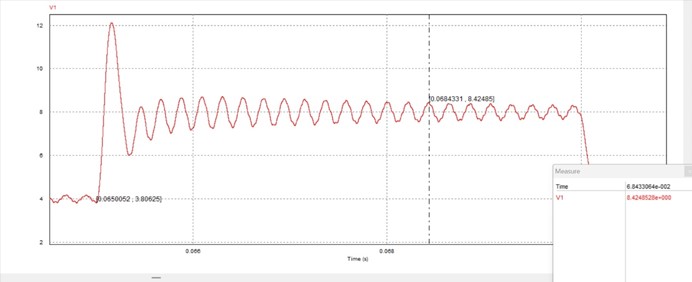
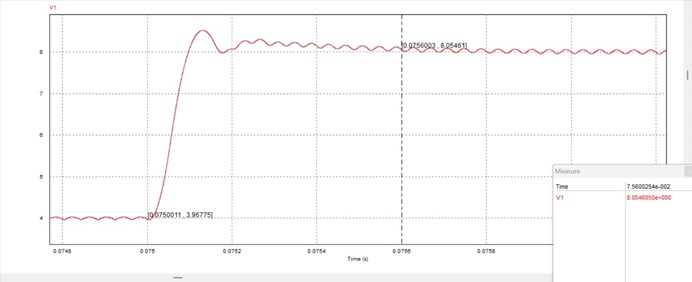
为反映超前校正的引入对于系统暂态响应速度的提升效果，搭建PSIM仿真电路，分析校正前后参考电压跳变瞬间的输出电压响应情况：
对比校正前后参考电压跳变瞬间的输出电压暂态响应PSIM仿真结果，可以发现：校正前系统暂态响应时间约为0.034s，而加入超前校正环节后系统暂态响应时间为0.0006s，较校正前有显著缩短，说明超前校正的引入有效提升了系统的动态响应特性（快速性）。
6.3 PI+微分环节D（PID）分析设计 除增加串联超前校正环节设计外，还可以通过在原有PI控制器基础上加入微分环节D实现PID闭环控制来提升系统的稳定性与暂态响应速度。事实上，在PID控制器的三个环节中，比例环节P主要负责动态性能的提升，积分环节I主要负责稳态精度的提升，而引入微分环节D则可进一步改善系统的稳定裕度以提升系统稳定性。
与PI控制器类似，通过对PID控制器的微分方程组进行拉普拉斯变换，可以得到其传递函数为：
接下来将通过MWorks绘制波特图，配合PSIM的扫频仿真结果，从相位裕度的角度来反映微分环节D的引入对于系统稳定性的提升：
对于PI控制器，给定控制器参数:
1 2 3 4 5 6 7 8 9 10 11 12 using TyControlSystemss=tf('s' ); vm=1 ; r=2 ; esr=0.107185 ; c=6.6 *10 ^(-4 ); l=10 ^(-4 ); vg=15 ; kp=0.12 ; tao=1 /5000 ; G=kp*(tao*s+1 )\*(esr*c*s+1 )*vg/(tao*s*vm*(l*c*(1 +esr/r)*s*s+(l/r+esr*c)*s+1 )); bode(G);
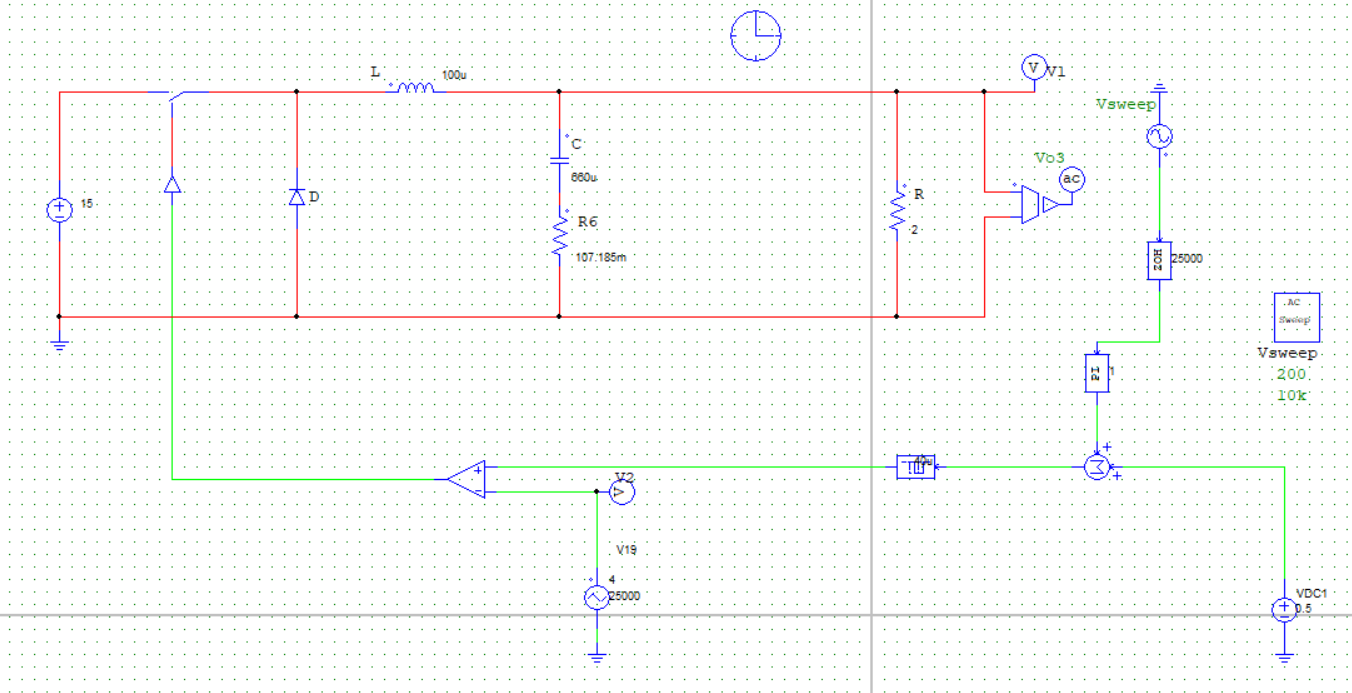
同时在PSIM中搭建扫频仿真电路，通过扫频仿真结果验证MWorks绘制波特图的正确性：
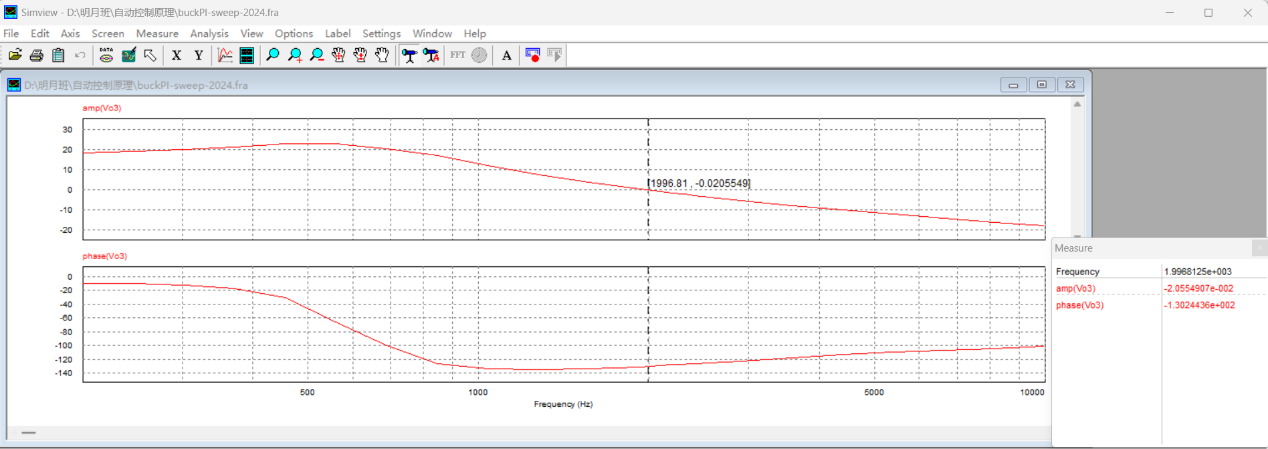
从图中可读出：PI闭环控制系统剪切频率
对于加入微分环节D后的PID控制器，给定控制器参数:
1 2 3 4 5 6 7 8 9 10 11 12 13 using TyControlSystemss=tf('s' ); vm=1 ; r=2 ; esr=0.107185 ; c=6.6 *10 ^(-4 ); l=10 ^(-4 ); vg=15 ; kp=0.12 ; tao=1 /5000 ; taod=0.00001 ; G=(kp*(tao*s+1 )+taod*tao*s*s)*(esr*c*s+1 )*vg/(tao*s*vm*(l*c*(1 +esr/r)*s*s+(l/r+esr*c)*s+1 )); bode(G);
同时在PSIM中搭建扫频仿真电路，通过扫频仿真结果验证MWorks绘制波特图的正确性：
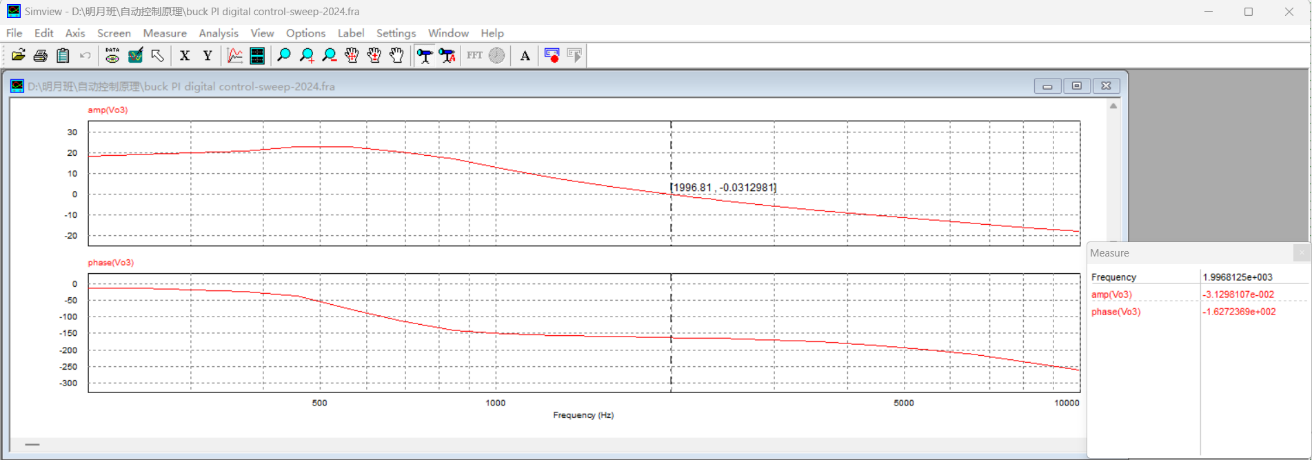
从图中可读出：PID闭环控制系统剪切频率
通过对比PI和PID控制下的波特图与扫频结果可以发现，相比于PI控制器，PID控制下的直流Buck变换器闭环系统具有更高的相位裕度，这意味着在加入微分环节D之后，系统具有更好的稳定性。
6.4 PID控制PSIM仿真（校正前后R变化时输出电压分析） 为反映微分环节D的引入对于系统稳定性与响应速度的提升效果，搭建PSIM仿真电路，分析PI与PID控制器在负载电阻R不同时输出电压响应情况：
对比PI与PID控制器在负载电阻R不同时的输出电压暂态响应PSIM仿真结果，可以发现：当负载电阻R=2Ω时，在原有的PI控制器闭环控制下，系统的暂态响应时间约为0.008s，而加入微分环节D后，系统在PID控制器的闭环控制下暂态响应时间为0.004s，这意味着在加入微分环节D后，系统的动态响应特性得到一定提升（响应时间缩短50%）；除此之外，在相同的控制器作用下，随着负载电阻阻值由2Ω增大到5Ω，系统的输出电压在稳定后的振荡幅度明显减，但此时暂态响应时间也明显增加（增加近两倍）。
6.5 本章小结 本章主要介绍了基于PI控制器的校正设计，对于直流Buck变换器的闭环控制而言，分别采用在原有控制系统上增加超前校正环节与微分环节D的两种校正方式实现复合PI控制，通过MWorks绘制波特图与PSIM扫频仿真，反映校正环节的引入对于相位裕度即系统稳定性的提升效果，并结合PSIM电路仿真的输出电压结果，观察校正环节的引入对于系统暂态响应速度即动态响应特性的提升效果。仿真实验结果表明，对于PI控制器的校正设计（超前校正/引入微分环节形成PID控制）在提升系统稳定性与动态响应快速性方面取得了良好的效果。
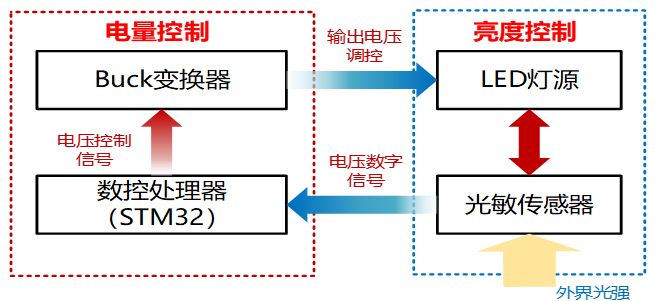
7 基于直流电源调控的自动调光控制设计 该系统的主要功能是将灯的电压通过直流Buck变换器完成闭环PID控制，将输出电压控制在0-15V范围内。系统主要包含电量控制与亮度控制两个部分，其中电量控制由STM32数字控制器通过电压控制信号调节Buck变换器输出电压；亮度控制则通过光敏传感器感知外界光强，并将反馈信号传递给STM32，实现对LED灯源亮度的动态调整，从而形成电压与亮度的双闭环调节系统。
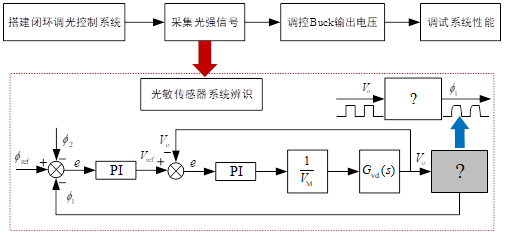
基于该架构，系统设计的基本流程如下：
搭建Buck电路控制系统，用于调控LED灯源；
使用开发工具Keil5编写STM32控制程序，实现PWM信号生成和调节；
将光敏传感器的输出连接到STM32的ADC（模数转换器）端口；
设计闭环控制系统并编写主控程序，实现根据光照强度自动调节PWM占空比，从而控制LED灯光的亮度；
调试系统，过程中实时监测电路工作状态，确保电路安全稳定运行且光照强度变化时LED灯亮度能够迅速进行响应调整；
对系统功能进行测试与优化，验证系统的响应速度和调光精度。
除此之外，在系统基本功能的设计实现基础上，还进行了基于无线通信的远程控制这一拓展功能设计，将调光系统与蓝牙无线通信模块结合，实现通过手机应用对LED灯进行调光控制，增加系统的便携性和灵活性。
接下来将分模块具体阐述自动调光控制系统各功能设计的详细过程。
7.1 默认电压值设置 在系统上电之后，输出电压默认设置为9V。之所以选择9V作为默认值，是因为这一电压能够在不消耗过多能量的情况下提供足够的亮度，同时避免由于过高或过低电压对系统性能的影响。
具体来说，9V的默认值具有以下几个优点：
（1）能耗平衡：相较于较低电压（5V），9V能够提供更高的亮度输出，同时不会像满电压（15V）那样带来显著的能量消耗，适合作为常规环境下的起始亮度。
（2）避免电压冲击：在系统刚启动时，设定较高的默认电压可能会导致电流冲击，影响电源和负载的寿命。9V作为中间值，有效降低了这种风险。
（3）用户体验优化：默认电压为9V时，灯光亮度适中，避免了开机过亮或过暗对用户造成的不适，同时为后续手动或自动调节提供了便利。
（4）环境适应性：在普通家庭或办公室环境下，9V的亮度通常能满足基本照明需求，而无需立即调整，增强了系统的即用性。
此外，9V的默认值通过主程序固化设置，确保每次系统启动时都能快速恢复到该默认电压值。这一设置不仅提高了系统的稳定性，还为后续用户操作提供了可靠的初始状态。设计中对默认电压的选择经过多次实验验证，综合考虑了实际照明需求和电源性能，最终确定了这一合理数值。
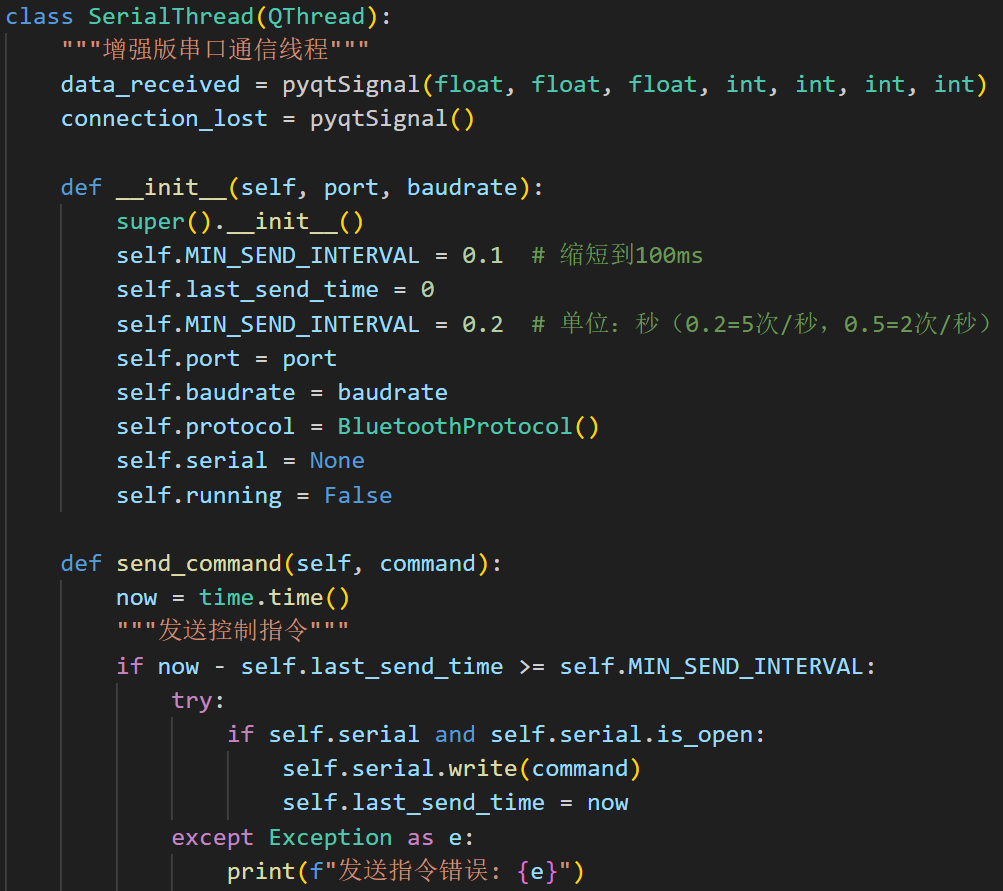
7.2 蓝牙接口通信控制 在本系统中，蓝牙模块被用作与手机或其他移动设备的通信桥梁，用户可通过蓝牙实现对灯光的远程控制，增强系统的操作便利性和用户体验。蓝牙模块选用低功耗蓝牙（Bluetooth Low Energy, BLE）技术，保证了通信的可靠性和功耗优化。具体而言，蓝牙通信具有以下优点：
便捷性：用户可通过手机远程调节灯光，无需物理接触，尤其适合家庭场景。
可扩展性：蓝牙接口支持更多功能指令的扩展，如灯光模式切换等。
低成本实现：蓝牙模块硬件成本低，结合STM32可轻松实现稳定通信。
以下是蓝牙接口通信功能的详细设计：
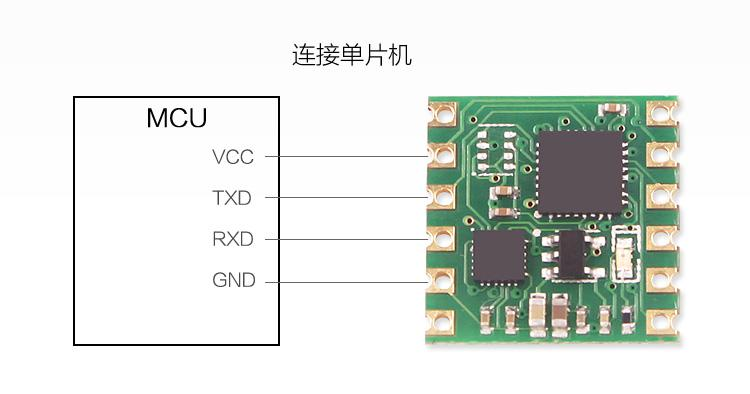
硬件接口设计
软件功能设计
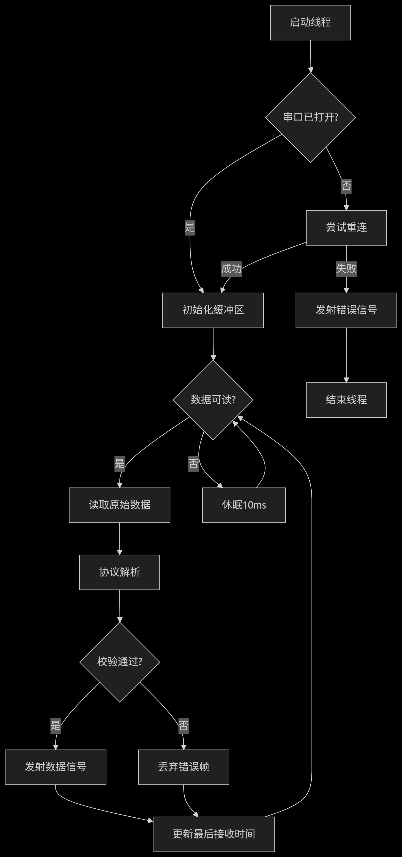
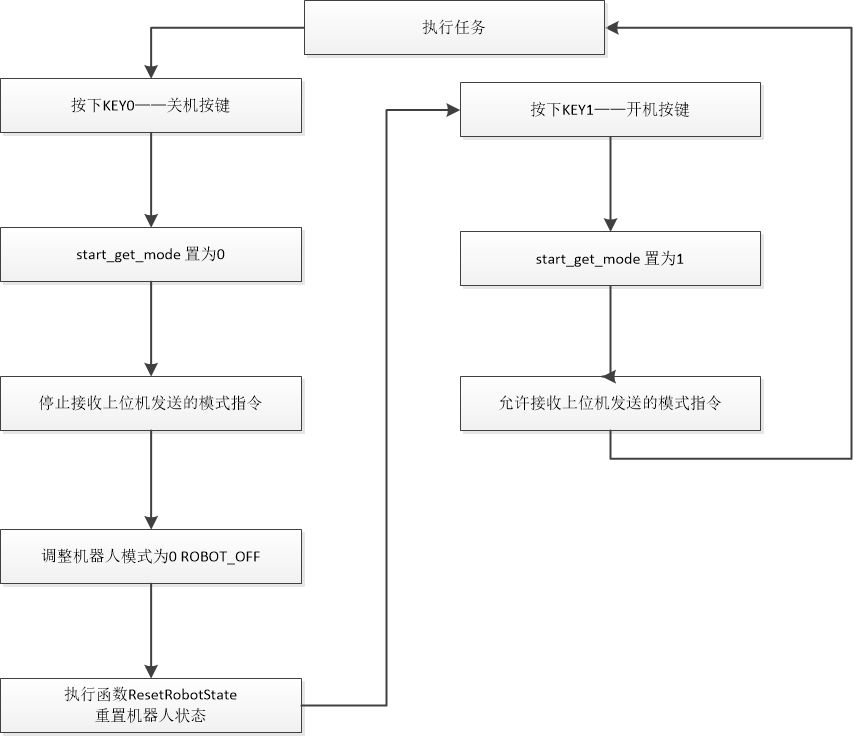
蓝牙通信通过STM32主程序实现对蓝牙模块接收指令的解析和响应。指令的解析流程大致是这样的：主程序中设定一个蓝牙接收缓冲区，用于存储用户发送的指令；当蓝牙模块接收到数据时，触发中断，将数据写入缓冲区；程序定时轮询缓冲区，并根据指令类型解析执行以下指令以实现功能，包括灯的开关、亮度百分比调整，以及环境光自动调节的触发：
“on”/“off”指令：通过电压直接跳转的方式实现即时开关
“on”：将输出电压设定为最大值15V，点亮灯光；
“off”：将输出电压设定为最小值0V，关闭灯光。
通信协议设计
蓝牙通信基于简单的ASCII协议，用户可通过手机APP或终端工具发送指令。每条指令均以换行符\n结尾，便于解析。以下是通信协议的具体格式：
“on\n”：开启灯光。
“off\n”：关闭灯光。
“50\n”：将亮度设置为50%。
“LL\n”：启动环境光度自动调节模式。
通过蓝牙接口通信，系统不仅支持手动调节灯光，还为后续的智能化功能扩展奠定了基础。
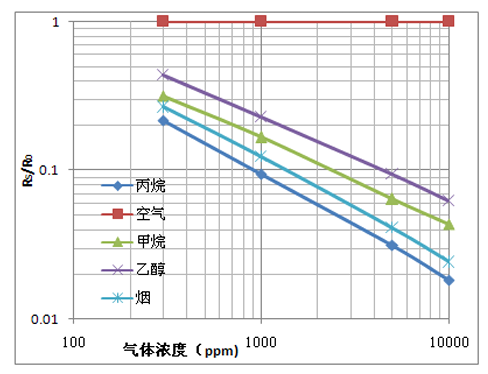
7.3 基于光敏传感器的调光功能 本系统采用光敏传感器对环境光强进行实时检测，并基于检测值动态调整灯光的亮度，提供适应不同场景的自动调光功能。通过光敏传感器实现调光，既可以减少用户手动调整灯光的频率，还可以自动优化输出电压，适用多种场景需求。通过闭环控制机制，确保灯光的输出电压与环境光强度的变化相匹配，为用户提供更舒适、高效的照明体验。以下为光敏传感器调光功能的详细设计与实现过程：
硬件接口设计
软件功能设计
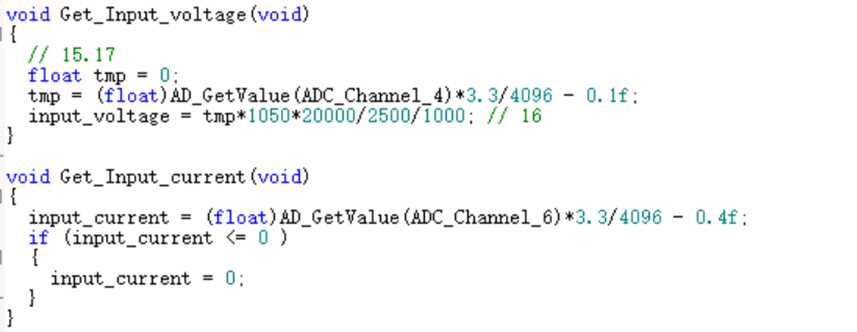
数据采集与转换：STM32通过ADC模块以一定采样频率读取光敏传感器的模拟信号，模拟值范围为0到4095，对应电压范围为0到3.3V；可通过公式
调光逻辑与策略：当ADC值低于预设阈值（如1024）时，认为环境光较暗，此时系统逐步增加输出电压，以提高灯光亮度补偿环境光；当ADC值高于预设阈值（如3072）时，认为环境光较亮，此时系统逐步降低输出电压，以避免浪费电能或造成视觉不适；当光强处于中等范围时（ADC值1024到3072），输出电压以线性比例动态调节，保持环境与灯光亮度的适应性平衡。
PID闭环控制：根据光敏电阻值计算目标电压，并作为参考值输入PID控制器；PID控制器实时计算实际输出电压与目标电压之间的误差，并调整PWM信号占空比控制Buck变换器，确保输出电压快速稳定地收敛到目标值。
状态反馈与异常处理：当光敏传感器信号异常（如ADC值恒定不变或超出有效范围）时，系统进入保护模式，将输出电压设定为安全值9V，并通过蓝牙模块通知用户；传感器数据每次读取后均存储在缓冲区中，并定期更新，避免因单次采样噪声造成调光不稳定。
为进一步验证调光功能的灵敏度，需要测试光敏传感器在不同光强条件下的响应时间和精度，确保其采集的光强信号与实际环境光强相符。经过调试，光敏电阻灵敏度较高，但光敏电阻的朝向会对空间中同一点的光敏传感有不同的值。解决方式为固定光敏电阻朝向位置，使其主要接收来自上方的环境光。除此之外，还需要验证在自动调光模式下，灯光亮度调整是否与环境光变化相匹配。经过我们的实验，该灯泡在8V电压以下不会发光，且为了保护电路和用户，我们将最高输出电压15V通过程序限制在12V，于是我们将光亮百分比线性映射公式修改为：
为进一步优化用户的使用体验，还开展了用户测试实验为产品优化提供参考。实验记录了光敏传感器自动调光时用户的视觉体验，并通过调整PID参数和映射公式提高舒适性。通过光敏传感器的引入，本系统实现了基于环境光强的自动调光功能，显著提升了灯光控制的智能化水平与用户体验。
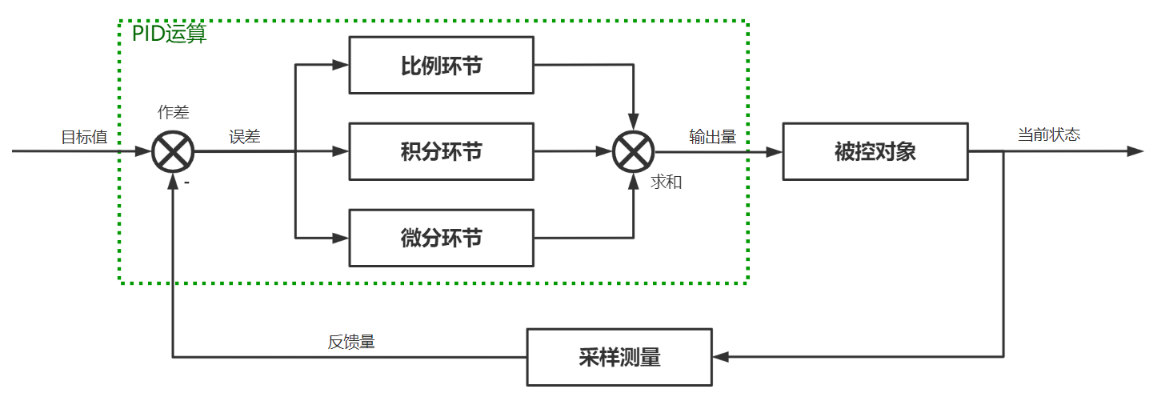
7.4 闭环PID控制原理 闭环PID控制是本系统的核心功能之一，负责根据目标输出电压值和实际输出电压值的误差，动态调节PWM信号，从而控制Buck变换器的输出电压，实现稳定、精准的调光效果。通过PID控制算法，可以使Buck变换器的输出电压始终接近目标值，无论输入电压波动、负载变化，还是环境光强条件改变，都能够保持系统的高稳定性和快速响应性。
PID控制算法主要由三部分组成：比例（P）、积分（I）、微分（D），可通过公式
通过调节K_p,K_i,K_d三个参数，可以调整控制器的性能，从而实现系统响应特性的优化，提升系统控制效果。具体而言，三个参数对于响应输出的影响如下：
比例（P）参数K_p：比例项主要控制误差对输出的直接影响，增大K_p会使系统响应更迅速，但过大可能引起震荡。本系统初始设置
积分（I）参数K_i：积分项通过累积误差消除稳态误差，确保输出精度。由于积分过大会导致超调或积分饱和，本系统设置
微分（D）参数K_d：微分项对误差变化率进行调节，用于改善动态性能并抑制震荡。为避免过分灵敏的微分效应引入噪声，D参数设置为较小值
在本项目的自动调光系统中，PID控制器的控制流程主要分为如下几个步骤：
误差计算：STM32单片机实时采集目标电压值 V_target 和实际输出电压值 V_actual，计算误差：
控制信号计算：根据误差值，通过PID公式计算控制信号u(t)，调整PWM信号的占空比：
PWM调节：将计算得到的u(t)映射为PWM信号的占空比，直接控制Buck变换器的输出电压。占空比范围为10%至80%，对应输出电压范围为0V至15V。
反馈调整：系统持续监测实际输出电压，更新误差值并重复上述步骤，形成闭环控制。
在基于STM32单片机编写程序具体实现PID控制器算法时，还需要特别注意以下两点：
在实际调试验证时，主要对于控制系统的动态性能与抗干扰能力进行了测试与优化，以进一步提升自动调光功能的灵敏性与稳定性，从而优化用户体验：
最终经过多次调试与不断优化，该闭环PID控制系统实现了以下目标：
7.5 外观设计制作 为了使本系统不仅具有实用性，还能满足美观性和设计感的需求，我们对外观部分进行了重新设计和制作。本节详细介绍了外观设计的灵感来源、制作过程以及技术实现中的注意事项。
本系统的外观设计灵感来源于游戏《无畏契约》（Valorant）中的角色”尚博勒”（Chamber）的道具”摄像头”。这一设计概念契合科技感与现代感的视觉效果，适合科技爱好者的审美需求，同时其独特的造型也为灯具的装饰性增色。我们力求将其视觉元素融入本项目，打造一款既具功能性又有极高辨识度的灯具设备。同时在外壳设计时也结合了灯泡的散热需求，保证了灯具长时间工作时的安全性和稳定性。设计中注重可拆卸性，用户可以方便地调整灯泡朝向和光照亮度。
详细的制作过程如下：
原型拆解
我们首先将旧灯具的灯罩部分锯下来，仅保留其内部核心组件，包括灯泡、散热装置、电路板和连接线。为确保灯具正常运行，对保留的灯泡和电路板进行功能检测，确认其性能稳定，并清理了原型中多余的固定结构，为后续的外壳重新设计预留空间。
3D建模与设计
使用Fusion 360软件，根据”尚博勒摄像头”的设计特点，建模了一个以球体和多面体造型的外壳结构。模拟摄像头的结构，在灯具上设计了圆形凹陷部分，提升灯具的科技感。外壳设计了散热格栅，与灯具散热需求相结合；外壳底部设计了支撑脚架，便于放置和移动。摄像头部分设计轨道凹槽，可旋转控制摄像头方向。
材料选择与加工
外壳部分采用轻质耐用的 PLA 材料，利用3D打印技术制作。打印分为两个部分：上半部分为灯具主壳，下半部分为安装支架，组装后固定。3D打印完成后，外壳表面进行手工打磨并喷涂金色亚光涂料，灯罩边缘则涂上金属漆，营造高科技感。
组件安装与调试
将灯泡、电路板、散热器嵌入3D打印外壳中，通过卡扣、限位固定，确保结构稳固。为避免外壳对散热产生影响，在装配后对设备进行长时间运行测试，确保温度稳定在安全范围内。重新调整灯光的投射方向和亮度，使其与设计的外壳结构匹配，确保在不同环境下具备良好的照明效果。
为进一步提升用户体验，后续将持续对产品进行深度优化，包括添加更多灯光模式（如动态光效或多色渐变）以进一步增强装饰性和互动性，或引入语音控制功能并将其与蓝牙通信相结合以提升智能化体验。
7.6 本章小结 本章介绍了基于直流电源调控的自动调光控制设计，通过蓝牙模块完成手动输出电压控制，通过光敏传感器进行环境光度自动调节，最终通过Buck变换器闭环PID控制完成灯的电压和光亮度稳定。
8 基于直流电源调控的光伏MPPT控制设计 8.1 设计背景与系统架构 光伏发电是当前清洁能源的主流之一，最大功率点跟踪（Maximum Power Point Tracking, MPPT）是光伏系统中提高效率的关键技术。由于光伏板的输出功率受到光照强度影响，不同的光照强度下最大功率点对应的输出电压不同，需要不断通过改变输出电压来寻找最大功率点（MPP）。因此，希望通过搭建一个基于直流电源调控的光伏MPPT控制系统，结合STM32单片机和Buck变换器实现光伏阵列的最大功率点跟踪，从而使得系统维持在最大功率工作，减少不必要的能量损失，有效储存其他能量转化成的电能。
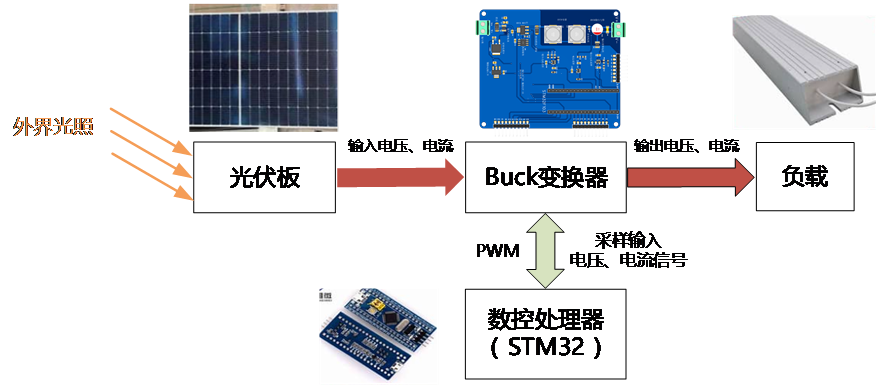
在该系统中，外界光照被太阳能电池板转化为电能，经功率变换电路处理后向负载供电。STM32微控制器实时采集电池板电压、电流等参数，运行MPPT算法，生成控制信号优化功率变换电路的工作状态，确保太阳能电池板始终在最大功率点运行，提高能源利用效率。
8.2 实验原理 光伏板的输出功率会受到环境条件（如光照、温度）影响，这一点无法改变，但是输出功率同时也受到工作电流、电压的因素影响，因此可以通过调节负载电压，使光伏系统的功率维持在最大值，即工作在最大功率点（实现输入侧阻抗匹配）。在本课程使用的Buck变换器中，可以根据STM32输出PWM波的占空比来控制输出的电压，同时由于电路中在不断采集输出电压，从而可以通过设计相应的控制算法算法实现对于输出电压的精确闭环控制。
为了找到最大功率点，可采用扰动观察法（Perturb and Observe, P&O）算法。通过降低与增加占空比来调节输出电压，由于电阻一定，可以通过计算算出变化后的功率，同时将其与变化前的功率进行比较，若功率增大，则沿当前方向继续调整占空比；否则反向调整。在每次调整占空比后，计算功率并记录趋势，从而找到最大功率点。在本项目中，采用改进的扰动观察法，通过记录功率变化并自动调整占空比，从而快速收敛到最大功率点。
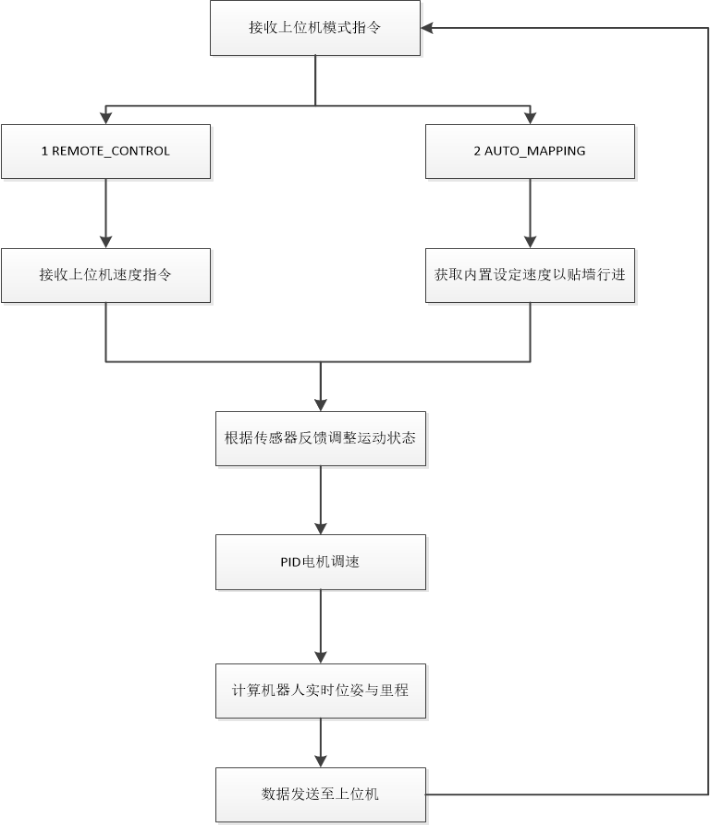
8.3 代码逻辑 在Keil5中编写的STM32主控代码主要分为如下4个主要的功能模块：
系统初始化：初始化系统时钟与ADC、PWM模块，为数据采集及控制做好准备。
1 2 3 4 SystemInit(); PWM_Init(); AD_Init(); _enable_irq();
PWM控制模块：通过实时调控PWM输出占空比实现Buck变换器输出电压的改变，从而影响光伏阵列的工作点。值得注意的是，需要调整PWM输出频率与Buck变换器相适应，同时确保输出占空比范围在0~1范围内。
1 2 3 TIM_OCInitStructure.TIM_OCMode = TIM_OCMode_PWM1; TIM_OCInitStructure.TIM_Pulse = 0 ; TIM_SetCompare1(TIM2, (uint16_t )(dutyCycle * PWM_PERIOD));
ADC采样模块：将光伏阵列输出的电压信号通过ADC采样转换为数字信号并读取，再通过与电阻的计算得出电流值，以用于功率计算。值得注意的是，ADC通道需与光伏阵列信号对应，同时为确保采样精度还需事先对ADC模块进行校准。
MPPT算法实现：根据扰动观察法原理，通过电流与电压相乘得到当前输出功率，与上个点的功率相比较，若大于上个点的功率，则继续增大占空比，增加输出电压，从而增加输出功率，若小于，则减小占空比，并在每次调整占空比后再次计算输出功率。循环往复进行上述流程，同时记录功率变化趋势及对应占空比，以寻找最大功率点。值得注意的是，程序中设置的步长STEP_SIZE值应适中，过大会导致振荡，而过小则会影响跟踪的速度，同时还应避免控制过程中PWM波形的占空比超出0~1范围。
在主循环main函数中编写总控代码对上述代码逻辑进行整合，每次循环都会测量电压与电流从而得到功率，再通过进行扰动观察法寻找最大功率点。
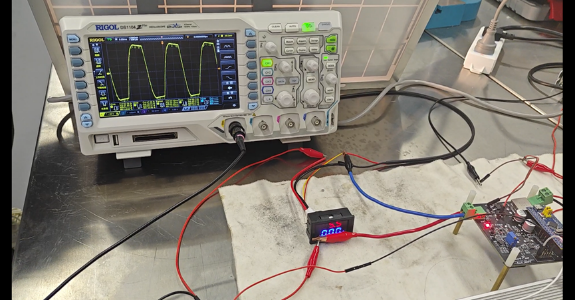
8.4 实验现象 实验时，将Buck变换器、STM32开发板与光伏阵列进行连接，并确保采样与控制电路正常工作。将代码烧录到STM32开发板，并通过调整光照强度，观察功率点变化及最大功率点跟踪效果。接下来需要进行逐步调试：
使用示波器观察PWM信号及Buck变换器输出电压，验证占空比调节是否正常，并使用万用表验证电压、电流采样值是否准确；
可以看到，此时PWM输出占空比为50%，占空比调节正常；光伏板输出电压为5.1V，电流为0.025A，输入功率约为0.1275W。
通过调整光照强度，观察功率点变化及最大功率点跟踪效果。
可以看到，此时所接负载为200Ω，输出电压为4.5V，输出功率约为0.12W。考虑功率损耗，光伏板输出功率约等于负载消耗功率，完成了对该光照强度下最大功率点（MPP）的准确寻找。
随后又对于该控制系统的动态跟踪性能进行进一步的测试，可以观察到，当外界环境的光照强度改变时，控制系统能快速做出响应并使光伏板输出功率达到最大（约为负载消耗功率），说明控制系统对于最大功率点的实时跟踪性能良好。
8.5 本章小结 本章主要介绍了基于直流电源调控的光伏板最大功率点追踪（MPPT）控制系统的设计，设计时主要采用递归算法，每次通过扰动当前功将率与变换前功率作比较，若大，则继续增加占空比，若小，则减少占空比，以此类推，不断循环，从而找到最大功率点。每次变化占空比的步长与延时时间影响找到最大功率点的效率，需要调试找到最佳的相应效率。同时，在步长固定的情况下，通过自适应步长控制算法也可以更有效率的寻找最大功率。通过动态追踪，显著提高了光伏发电效率。
9 总结与展望 9.1 课程小结 《自动控制原理》课程作为一门项目制课程，重点围绕经典控制相关理论知识及应用实践，有效地将理论教学与设计实践结合起来。通过课程的理论学习与项目实践，我们在实践操作中对于经典控制理论的知识有了更加深刻的理解，建立了”控制”工程观与系统性分析思维，也锻炼了自己将理论应用于工程实践的能力，以及对于控制工程问题的分析与解决能力。
该项目制课程主要分为两个项目板块：
控制基础实践项目为”直流电源控制分析与系统设计”，以直流电源这一经典工程案例串联起经典控制理论知识各版块，涵盖控制系统建模（微分方程与传递函数）、时域分析、根轨迹分析、频域分析，频域校正与PID控制等，从理论分析、仿真、实验三维度强化同一理论知识点的学习，完成直流电源控制系统的分析设计以及调试。这一部分项目在理论课程学习的同时穿插完成，主要涉及到经典控制理论的学习，并将其应用到实际的Buck变换器PI闭环控制系统中、结合实际电路参数完成的PSIM电路仿真与相应的MWorks分析计算。
综合应用实践项目为”基于电源的综合应用系统”，以直流电源驱动系统应用为综合实践项目，运用传感、闭环控制、先进控制等硬件与算法，完成基于直流电源控制的LED自动调光与光伏最大功率跟踪（MPPT）等项目实践。这一部分项目主要以实验方式开展，最终本小组顺利完成实验与设计内容并进行课程项目汇报。
回顾这门课程一路走来，从课程引入与理论教学，到实际实验调试与项目设计，再到最终的项目测试与汇报，我们在理论与实践的结合中扎实掌握了经典控制理论的相关知识，并锻炼了自己的电路设计分析与实践能力。我们能取得如此的进步与成就离不开两位老师与四位助教的辛勤付出，在此再次向各位老师与助教们送上最真诚的感谢，也衷心祝愿这门课程在未来能建设得越来越好。
9.2 课程收获及建议 通过《自动控制原理》这门课程的学习，我了解到了许多经典控制理论的相关知识：从系统的数学建模入手，微分方程与传递函数是描述一个控制系统性能的基本工具；为调整系统参数以提高控制系统的稳定性，可从时域与频域两个角度分别进行分析，时域上可以使用劳斯判据进行系统稳定性的判定并根据根轨迹找到系统的临界稳定状态，频域上可以使用奈奎斯特稳定判据或依据Bode图对系统稳定性进行分析；基于频率特性，还可以从频域校正环节的设计层面调节系统的动态响应特性。理论学习之余，课程紧密穿插了相应的仿真与电路调试实验，理论与实践的结合使得我对于这些枯燥的理论知识有了更加生动而深刻的理解。
在课程项目中，我主要负责对于闭环控制系统的理论分析、仿真验证与参数调试，以及课程项目报告绝大部分的撰写。令我印象最深刻的是，在理论部分对系统进行频率特性分析时，使用MWorks根据系统开环传递函数绘制Bode图，得到了穿越频率与相位裕度；而在根据实际电路结构在PSIM中搭建了相应的扫频电路之后，当看到运行扫频仿真得到的结果与MWorks绘制的Bode图几乎完全一致时，我深刻体会到了理论的有效性，这代表理论的分析确实可以真实地指导实际控制系统的设计，在后续项目设计与调试时也充分利用了这一点，有效提高了设计与调试的效率。最终我们也顺利完成了基于直流电源调控的自动调光与MPPT控制系统的设计与实现，并将自动调光系统实例化为一个具有实际应用意义的产品。相信在这门课程中学到的知识与技能能够为我们未来的硬件产品开发中起到重要的作用。
最后感谢两位老师耐心的教学与指导以及四位助教的辛苦付出，特别是几位助教，耐心地回答我们的问题、批改我们的作业并协助我们进行硬件实物的调试，为我们的项目实践提供了丰富的参考资料，帮助我们快速上手项目。在此提出一点小小的建议，这次项目中在电路焊接方面浪费了许多时间，希望未来的课程项目设计能够在各个实现细节上更加完善，在设计与测试时考虑的更加全面；同时希望在理论课程中穿插的各种仿真作业能够与实际的控制系统结合的更加紧密，完善一些逻辑不严谨的地方（如提供的报告框架中，是否考虑电容寄生电阻这点体现的略显混乱）。但总的来说，这门课程确实是已有项目制课程中的精品，也希望能够在未来建设得越来越好。
参考文献 [1] 胡寿松主编.自动控制原理[M].科学出版社,2019:a670.
[2] 卢京潮主编.自动控制原理习题解答[M].清华大学出版社,2013:195.
[3] 王天威编著.控制之美[M].清华大学出版社,2022.
[4] 李昆.智能技术在室内LED照明系统中的应用研究[J].光源与照明,2024,(10):51-53.
[5] 郑盛梅.恒照度自动调光台灯的设计[J].光源与照明,2023,(01):69-71.
[6] 侯耀华,陈萍,於崇干.直流电源系统高级功能在无人值班变电站的应用[J].供用电,2015,(02):19-24.
[7] 许桂敏,解皓月,张子泉,等.基于Simulink的光伏电池特性及MPPT算法仿真研究[J].智能建筑电气技术,2024,18(06):36-39+60.
[8] 王青苗.PLC模糊PID控制系统在隧道照明节能控制中的应用[J].微型电脑应用,2024,40(06):114-118+122.
[9] 陈礼俊,兰志勇.单片机控制的双调控高压直流电源[J].现代电子技术,2017,40(12):165-168.
[10] 樊战亭,万欣,王超.太阳能电池板自动追光控制系统设计[J].咸阳师范学院学报,2024,39(06):12-16.
[11] Gene F. Franklin, J. David Powell, Abbas Emami-Naeini, et al. Feedback control of dynamic systems[M].Publishing House of Electronics Industry,2013:14,590.
[12] Karl Johan Astrom, Richard M. Murray.自动控制多学科视角[M].人民邮电出版社,2010:310.
附录 1 STM32闭环PI控制程序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 #include "stm32f10x.h" #include "Delay.h" #include "OLED.h" #include "PWM.h" #include "AD.h" #include "Serial.h" #define PWM_FREQUENCY 10000 #define MAX_PWM_VALUE 1000 #define PWM_PERIOD 3000 #define KP 0.1 #define KI 0.01 #define KD 0.01 float voltage_ref = 10 ; float voltage_fb = 0.0 ; float duty_cycle = 0.0 ; float error = 0.0 ; float integral = 0.0 ; float control_signal = 0.0 ; float last_error = 0.0 ; float derivative = 0.0 ; int sample_index = 0 ; float trueVoltage=0.0 ; float VREF;uint32_t time_counter = 0 ; uint8_t voltage_state = 0 ; uint16_t ADValue;float Voltage;float i;void control_buck (void ) { voltage_fb = (float )AD_GetValue()*3.3 /4096 ; trueVoltage = voltage_fb*1050 *20000 /2500 /1000 ; error = voltage_ref*2500 *1000 /1050 /20000 - voltage_fb; integral += error; derivative = error - last_error; control_signal = KP * error + KI * integral + KD * derivative; if (control_signal > 0.8 ) control_signal = 0.8 ; else if (control_signal < 0.2 ) control_signal = 0.2 ; duty_cycle = control_signal * PWM_PERIOD; i = (int )duty_cycle; PWM_SetCompare1(i); } int main (void ) { OLED_Init(); PWM_Init(); AD_Init(); Delay_ms(10 ); NVIC_Configuration(); Serial_Init(); while (1 ){ control_buck(); } }
2 自动调光程序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 #include "stm32f10x.h" #include "Delay.h" #include "OLED.h" #include "PWM.h" #include "AD.h" #include "Serial.h" #include "HC05.h" #include <string.h> #include <stdlib.h> #define PWM_FREQUENCY 10000 #define MAX_PWM_VALUE 1000 #define PWM_PERIOD 3000 #define KP 0.1 #define KI 0.01 #define KD 0.01 float Light_Intensity = 0.0 ; float voltage_ref = 5 * 1.38 ; float voltage_fb = 0.0 ; float duty_cycle = 0.0 ; float error = 0.0 ; float integral = 0.0 ; float control_signal = 0.0 ; float last_error = 0.0 ; float derivative = 0.0 ; float trueVoltage=0.0 ; float VREF;uint32_t time_counter = 0 ; uint8_t voltage_state = 0 ; uint16_t ADValue;float Voltage;float i;uint8_t RxSTA = 1 ;char RxData[100 ] = "N" ;void control_buck (void ) { voltage_fb = (float )AD_GetValue(ADC_Channel_4)*3.3 /4096 ; trueVoltage = voltage_fb*1050 *20000 /2500 /1000 ; error = voltage_ref*2500 *1000 /1050 /20000 - voltage_fb; integral += error; derivative = error - last_error; control_signal = KP * error + KI * integral + KD * derivative; if (control_signal > 0.8 ) control_signal = 0.8 ; else if (control_signal < 0 ) control_signal = 0 ; duty_cycle = control_signal * PWM_PERIOD; i = (int )duty_cycle; PWM_SetCompare1(i); } int main (void ) { OLED_Init(); PWM_Init(); AD_Init(); Delay_ms(10 ); NVIC_Configuration(); Serial_Init(); HC05_Init(); while (1 ){ HC05_GetData(RxData); if (RxSTA == 0 ){ if (strcmp (RxData, "LL" ) == 0 ){ RxSTA = 1 ; while (1 ){ Light_Intensity = (float )AD_GetValue(ADC_Channel_5); voltage_ref = (Light_Intensity * 2 / 3500 + 8 ) * 1.38 ; control_buck(); HC05_GetData(RxData); if (RxSTA == 0 ) break ; } } else if (strcmp (RxData, "on" ) == 0 ) voltage_ref = 10 * 1.38 ; else if (strcmp (RxData, "off" ) == 0 ) voltage_ref = 5 * 1.38 ; else { int num = atoi(RxData); if (num >= 0 && num <= 100 ) voltage_ref = ((float )num / 100 * 2 + 8 ) * 1.38 ; else if (num > 100 ) voltage_ref = 10 * 1.38 ; else voltage_ref = 5 * 1.38 ; } memset (RxData, 0 , sizeof (RxData)); strcpy (RxData, "N" ); RxSTA = 1 ; } control_buck(); } }
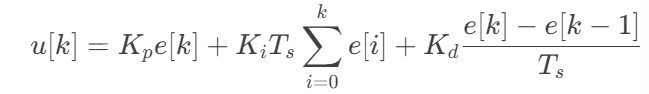
{width=”1.466816491688539in”
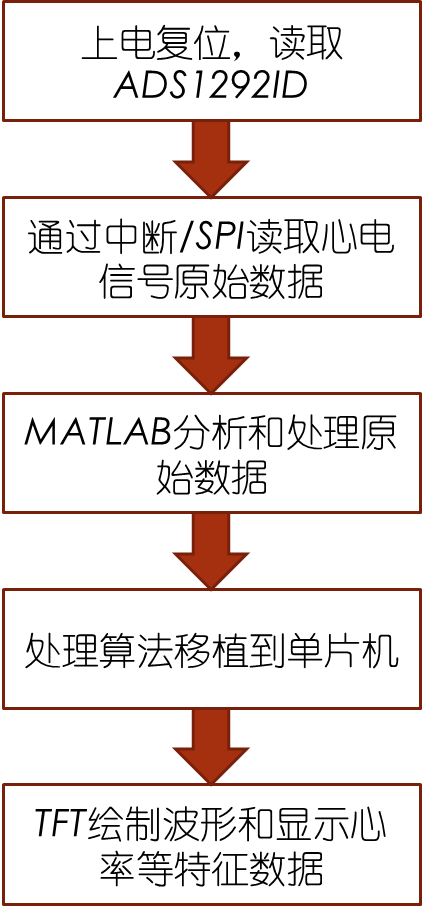
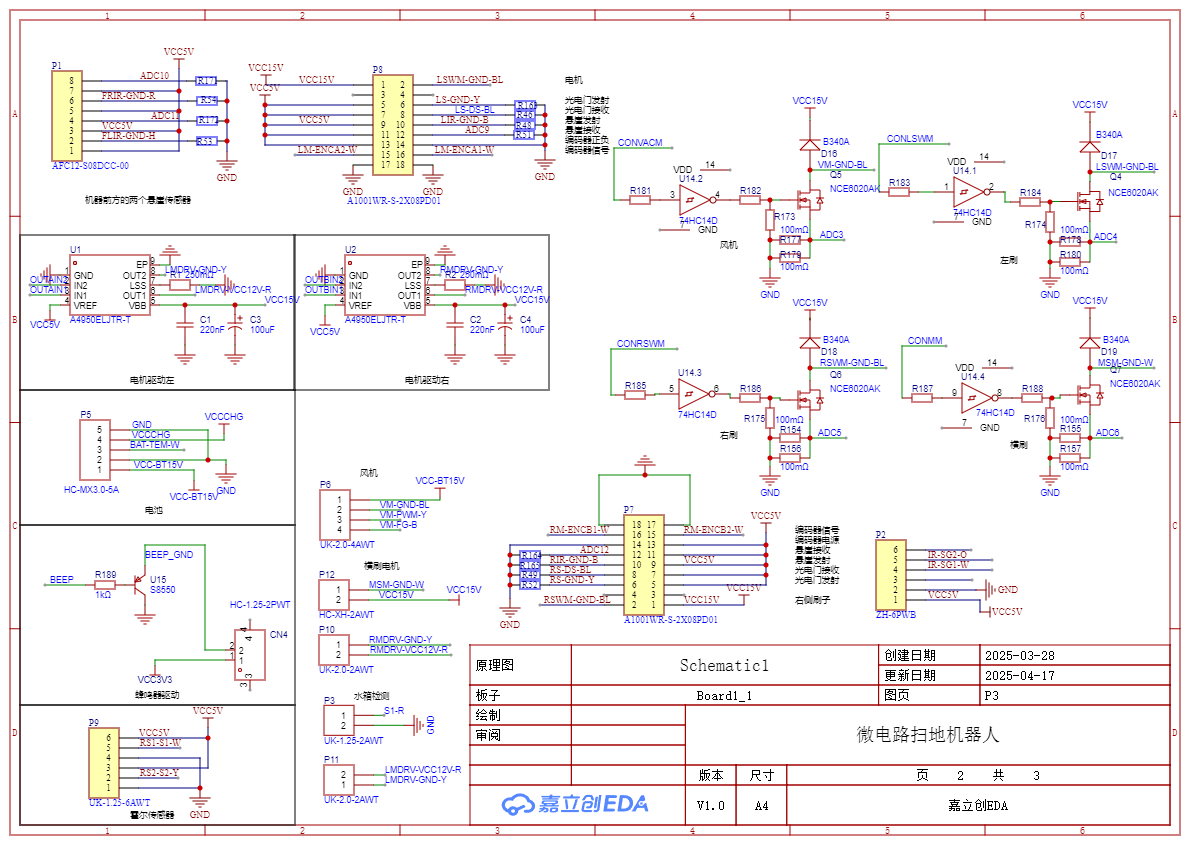
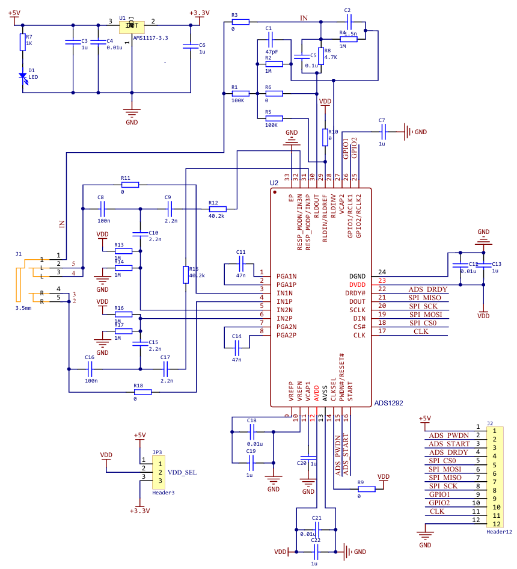该模块共有12个输出引脚（传感器模块右侧)，各引脚接口功能说明如下：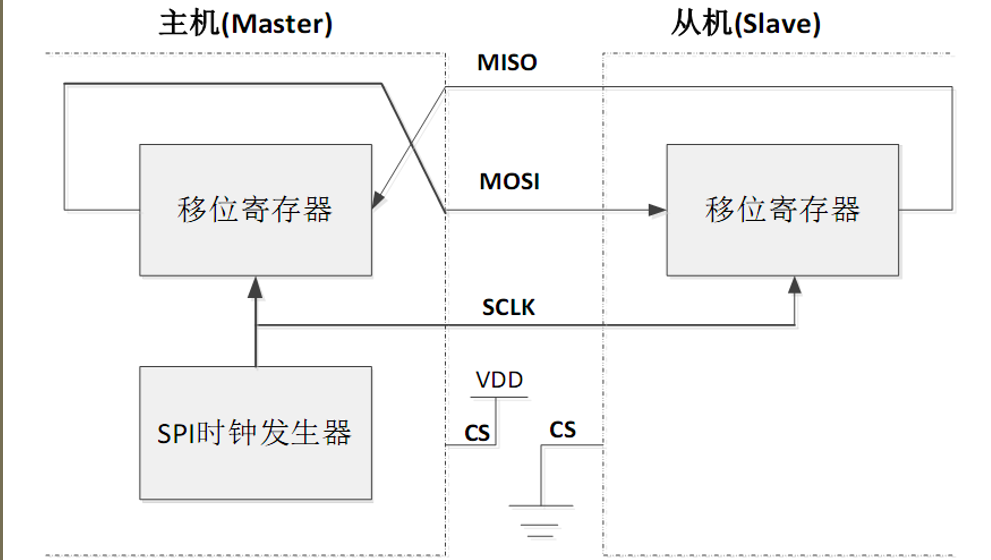
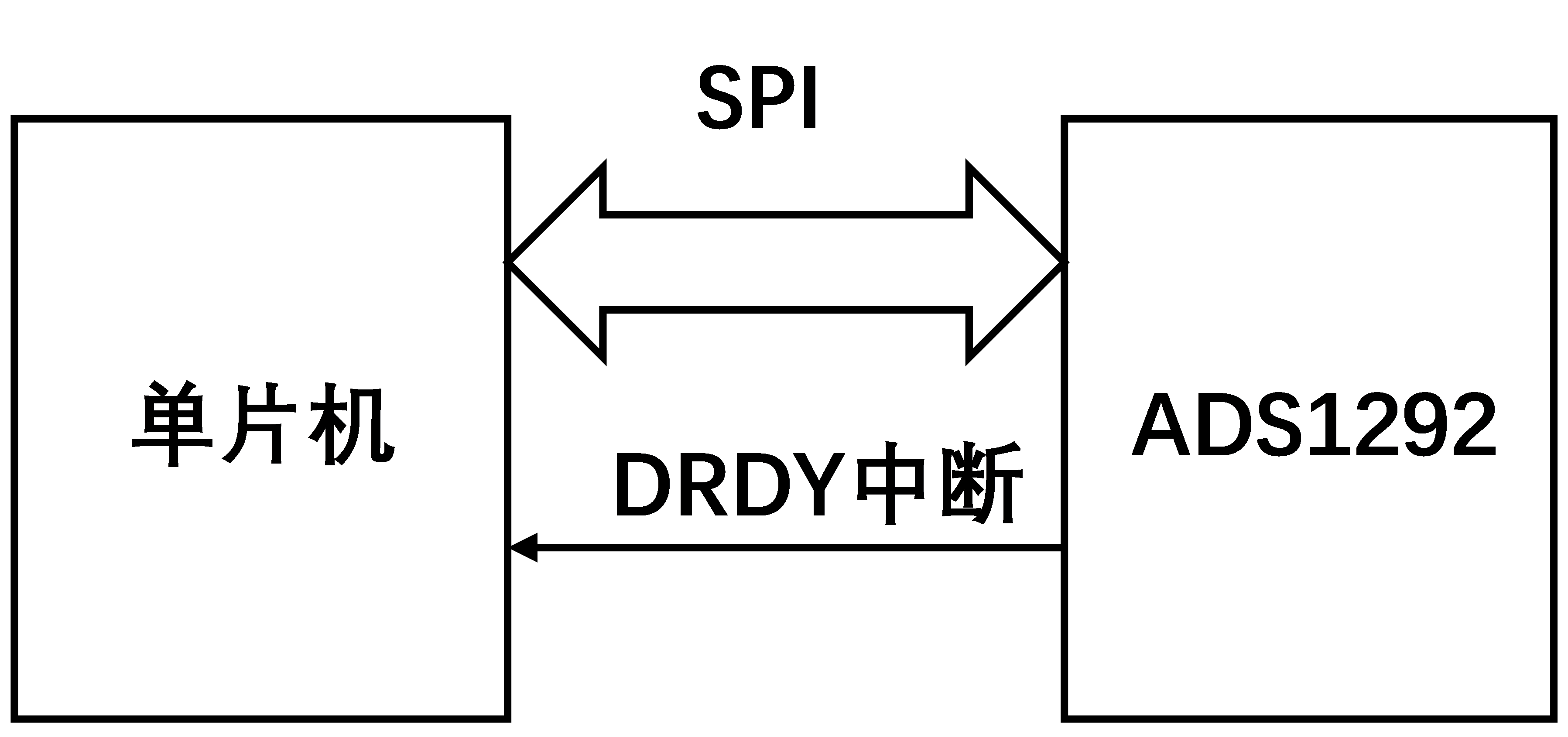
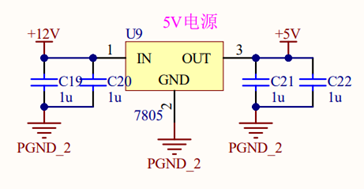
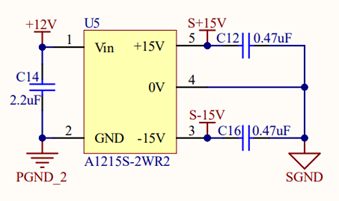
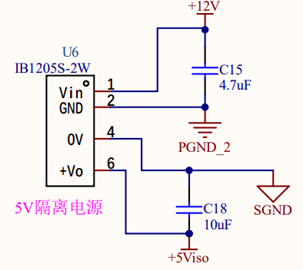
其次，在Buck变换主电路中，为满足设定元件参数，选取如下元器件：
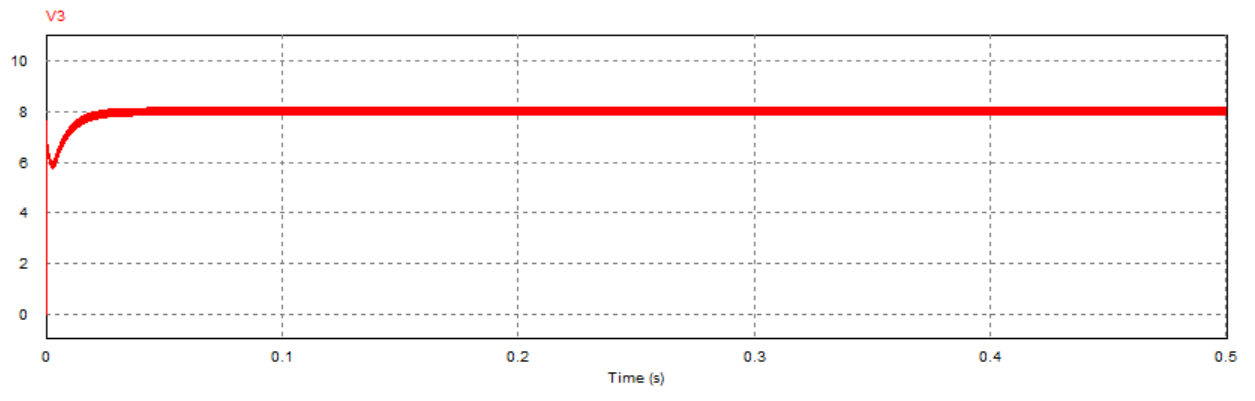
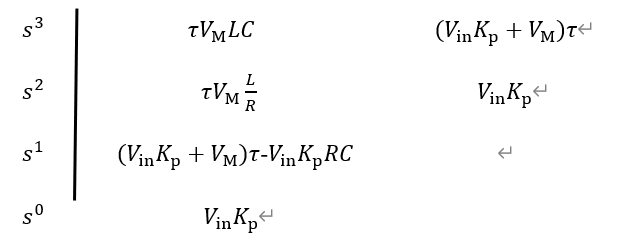
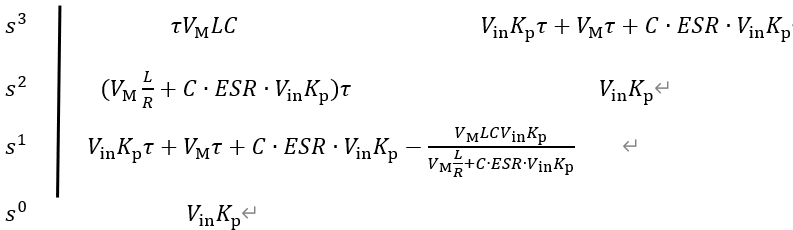
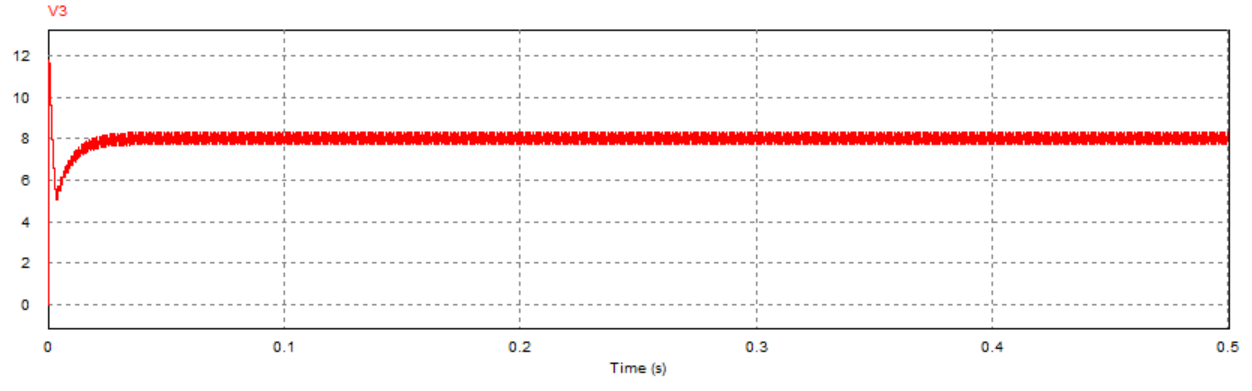
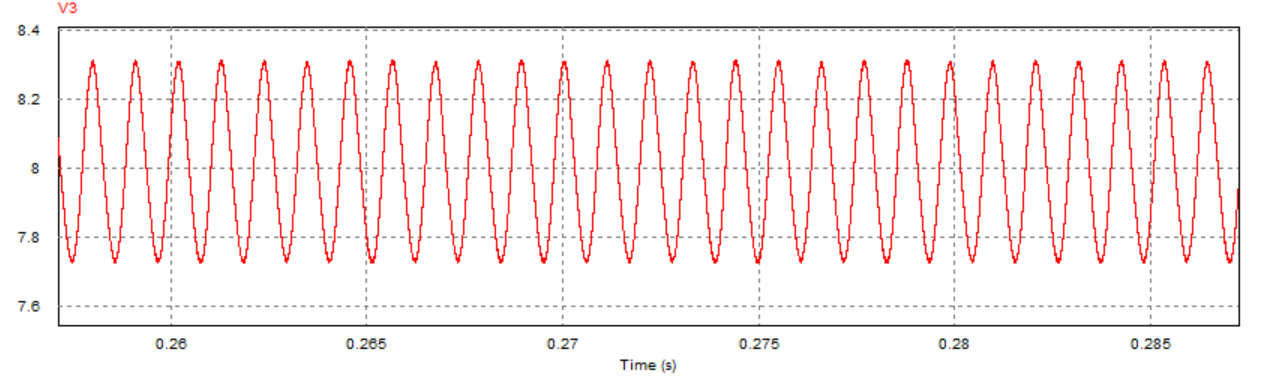
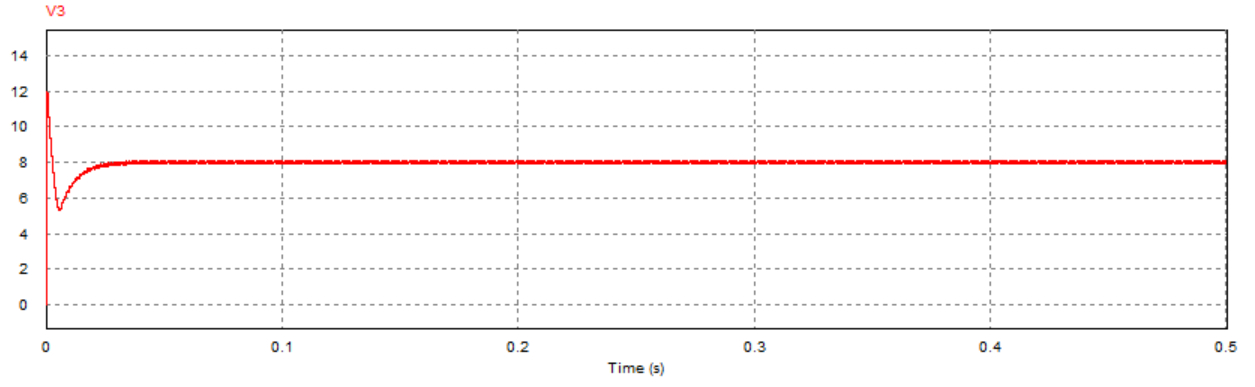
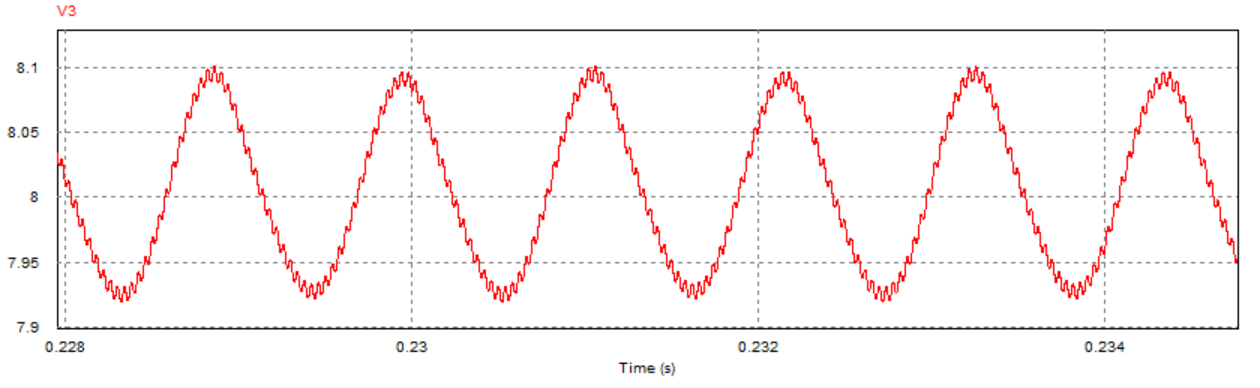取负载电阻值R=10Ω（大于临界值）时：
