选题背景与意义

微分方程是数学中一个重要且广泛应用的领域，涉及到描述变化和相互关系的方程。它是一种包含导数或微分的方程，常用于自然现象建模以及解决科学和工程领域中的问题。微分方程研究是数学中的一个重要分支，涵盖了广泛的领域和应用。通过研究微分方程，我们可以理解和预测自然现象的行为，以及解决科学和工程中的实际问题。同时，微分方程的研究也促进了数学的发展和数学工具在其他学科中的应用。

常微分方程被广泛应用于物理、生物、化学、经济学等各个领域。在许多情况下，观测数据是已知的，而其中隐含的微分方程仍然难以捉摸。因此，数据驱动的常微分方程(或动力系统)发现和反演是一个重要的研究方向。

微分方程反演问题是相对于微分方程的求解而言的：

• 微分方程的求解通常是一个正向问题，即给定初始条件，求解关于未知函数的方程；
• 微分方程反演问题是指根据已知的结果，推导出产生这些结果的微分方程，是从结果向方程的逆向推导和反演。

在数学上，微分方程的反演问题具有一系列的数学挑战和困难：

• 反问题的病态性：微小扰动在反问题的输出中会导致较大的误差，因此需要稳定性分析和正则化方法来解决数值计算中的误差；
• 存在非唯一解情况：需要利用先验信息、约束条件和经验知识等来进行问题的约束和规定，以得到合理的解。

微分方程反演问题研究在数学理论和实际应用中具有重要意义。通过解决微分方程的反演问题，我们可以从有限的观测数据中重建和推断未知的边界条件、初始条件或未知函数，从而深入理解系统的行为和性质，并提供科学、工程和医学等领域的相关应用。

随着计算机技术的发展，数值计算和机器学习在微分方程反演问题研究中的应用也呈现出迅猛发展的趋势。传统的微分方程推断方法依赖于领域专家的知识和经验，而机器学习方法，如神经网络、深度学习和遗传算法等，可以自动从大量数据中学习模式和关系，从而更准确地推断出微分方程模型。如今我们可以获取到大规模的、高维度的数据集，这为从数据中推断微分方程提供了更多的信息和挑战。而传统的模型推断方法在处理大数据集时可能受到维度灾难和计算复杂度的限制。机器学习的强大计算能力和自适应建模能力为解决这些问题提供了新的思路。

利用机器学习从数据中反演微分方程的方法可以分为两个方面：

• 在模型选择方面，机器学习可以通过自动搜索和学习合适的微分方程模型，利用测度函数或结构特征来评估不同模型的性能，并选择最适合数据的微分方程模型；
• 在参数估计方面，机器学习可以利用大数据集中的样本来优化微分方程模型的参数，以最小化模型与实际数据之间的误差。

利用机器学习从数据中反演微分方程是微分方程和机器学习交叉领域的重要研究方向。它利用机器学习的能力和大数据的优势，可以更准确地建模和预测复杂的动力学系统，推进科学研究和实际应用的发展。

针对常微分方程，目前常用的反演方法有如下几种：

• 高斯过程：将高斯过程置于状态函数之上，然后通过最大化边际对数似然性从数据中推断参数，这种方法适用于解决高维问题，但是对系统的形式有限制，并且仅用于估计系统的参数。
• 符号回归：创建并更正与观测数据相对应的符号模型，为控制函数提供更具表现力的函数形式，但缺点是对于大型系统来说计算成本高，并可能容易过拟合。
• 稀疏回归：找到候选基函数的稀疏组合来近似控制函数，其系数由最小二乘法或贝叶斯回归确定。这种方法提供系统的明确形式，不需要太多先验知识，但是依靠适当的候选函数；对于没有简单或稀疏表示的复杂动力系统来说可能是低效的。
• 统计学习：通过最小化经验误差来学习系统在某个假设空间中的相互作用核，避免维度诅咒，可以发现非常高维度的系统，但是仅适用于具有交互作用的核函数的动力系统。
• 物理信息神经网络（PINN）：一种新的深度学习方法，用于解决非线性偏微分方程的正问题和反问题。通过在前馈神经网络中嵌入由偏微分方程描述的物理信息，在不需要标签数据的情况下，将 PINN 训练为偏微分方程的近似解的代理模型。受此启发，进一步发展出了多步神经网络LMNets，这本质上是使用给定相点上的流映射提供的信息来反演动力系统种的未知控制函数f的一种逆过程。

在数值分析中，发展高阶方法是许多应用中的一个重要课题。传统上，在求解动力系统时，高阶离散化技术，如线性多步法和龙格-库塔方法已经得到了发展。近年来，线性多步法也被用于动力系统的发现。随着使用深度学习的发现取得令人满意的进展，对它在动力系统发现的理论理解也在进一步发展。

基于以上所陈述的微分方程反演问题的研究现状，针对无显式方程的非线性系统这一在真实物理世界中更为广泛且常见的情形，我们希望基于高阶离散化技术线性多步法，结合多步神经网络LMNets这一深度学习方法，拟合和反演出数据背后的动力学物理规律。

算法框架与原理

研究对象——常微分方程（组）

首先明确我们的研究对象——常微分方程：
$$
\begin{aligned}&\frac{dx(t)}{dt}=f(x(t),t),\&x(t_{0})=x_{0}\end{aligned}
$$
上述式子是一个最简单的二维常微分方程示例，其中x(t) ∈ R是关于时间t的函数，函数关系由一个微分方程刻画，且给出了一定的初值条件以唯一确定函数x的表达式，从而能够真实地刻画物理过程随时间变化的发展情况。

事实上大多数时候我们需要观测的物理量远远不止x这一个，因此为了后续更容易推广到高维情形（后续无特别说明，均围绕自治常微分方程展开讨论），我们将上述的非自治常微分方程转化为向量化的自治常微分方程：
$$
\begin{aligned}&\frac{d\boldsymbol{u}(t)}{dt}=\hat{f}(\boldsymbol{u}(t)),\&\boldsymbol{u}(t_{0})=\boldsymbol{u}{0}\end{aligned}
$$
其中：
$$
u=(x,y)\in\mathbb{R}^{D+1},\hat{f}=(f,1)^{T},u{0}=(x_{0},t_{0})^{T}
$$
在反演问题中，已知在若干时刻节点t_1、t_2、…、t_n的解x的数据，我们一般不会希望直接解出x(t)的表达式，而是通过确定光滑函数f，从而利用给定的数据反演出微分方程。这样的传统是从简单的反演情形推广并沿用的，因为比起得到一个精确的函数表达式，我们更希望探究这个表达式背后的物理规律，而这往往离不开微分方程，因此保留微分方程的形式具有一定的必要性。

多步神经网络

线性多步法是用于微分方程数值求解的常用方法。传统上，它们用于求解给定常微分方程的解，可以称为微分方程的正问题。但线性多步法也可以用于反演给定解的原微分方程，属于微分方程的反问题，尤其是将线性多步法的经典数值方法与神经网络相结合，例如多步神经网络。

线性多步法

线性多步法是求解常微分方程数值解的一种常见方法。随着计算机技术的发展，线性多步法得到更加广泛的应用。人们逐渐发现，在某些情况下，线性多步法可以提供更高的数值精度和数值稳定性。此外，线性多步法可以与其他数值方法（如龙格-库塔法）结合使用，互补彼此的优点。

对于上述常微分方程（非自治），设其中结点总数为N，时间间隔h为常数:
$$
h = t_{n + 1} - t_n, n = 1, …, N - 1
$$
则第n个结点的步长为M的线性多步法有以下公式：
$$
\sum_{m=0}^{M}[\alpha_{m}x_{n-m}+h\beta_{m}f(x_{n-m},t)]=0,n=M、\ldots、N, \alpha_{_M}\neq0
$$
使用线性多步法求解常微分方程时，必须选择初始的步长M值，以及确定系数α、β的不同方法，然后可以依次计算n≥M的近似值x_n。

事实上，根据确定系数的方法不同，线性多步法也分为多种类型，本项目中主要使用如下的三种常见的线性多步法：

• Adams-Moulton 法：作为一种隐式方法，需要通过迭代或其他数值求解技术来解决每个时间步长的方程组。它在求解非刚性和刚性常微分方程时都表现良好，并且具有较高的数值稳定性，其精度随步长的减小而提高，但响应地可能会产生更高的计算代价。对于高阶常微分方程，Adams-Moulton 法需要结合相应的差分格式将高阶常微分方程转化为一阶方程组进行求解。

$$
\sum_{m=0}^M\alpha_mx_{n-m}=h\sum_{m=0}^M\beta_mf(x_{n-m})
$$

• Adams-Bashforth法：作为一种显式方法，在求解非刚性和刚性常微分方程时都表现良好，计算效率较高，并且容易实现，但可能会收到稳定性条件地限制，其精度随步长的减小而提高。对于高阶常微分方程，Adams-Bashforth法需要结合相应的差分格式将高阶常微分方程转化为一阶方程组进行求解。

$$
\sum_{m=0}^M\alpha_mx_{n-m}=h\sum_{m=0}^M\beta_mf(x(t_{n-m}))
$$

• 后向微分公式法(Backward Differentiation Formula, BDF)：同样是一种隐式方法，但与Adams-Moulton法不同，后向微分公式法是通过解一个非线性方程组来得到当前时间步长的数值解。这个方程组可以用牛顿迭代等数值求解技术来解决。该方法具有较好的数值稳定性，其精度依赖于使用的插值多项式的阶数。一般来说，其高阶形式可以提供更高的精度，但也会增加计算的复杂性。它适用于求解非刚性和刚性常微分方程，并且在稳定性和数值精度方面通常有良好的表现。

$$
\sum_{m=0}^{M}\alpha_{m}x_{n-m}=h\beta f(x(t_{n}))
$$

除此之外，即使采用同一种系数确定方式，选择的步长M不同，得到的系数α、β也有所不同。具体而言，本项目中针对以上三种线性多步法，分别选取步长M=2/3/4的三种情况进行实验测试，下面列出各方法对应不同步长时的系数情况：

线性多步法的优点在于其高阶的精度和较小的计算代价，可以有效地逼近微分方程的数值解。但线性多步法可能会受到稳定性和初始条件的限制，选择适当的步长和求解方法非常重要。

多步神经网络算法

从线性多步法的公式中得到启发，可以用神经网络去反演常微分方程右端的f。通过相等时间间隔h的数值解x的数据训练神经网络，该神经网络的参数可以通过使以下均方误差损失函数MSE最小化来训练得到：
$$
MSE=\frac{1}{N-M+1}\sum_{n=M}^N\parallel y_n\parallel^2
$$
其中：
$$
y_n=\sum_{m=0}^M\left[\alpha_mu_{n-m}+h\beta_mf_{NN}(u_{n-m})\right],n=M,\ldots,N
$$
式中f_NN表示神经网络对函数f的近似，y_n也称为线性多步法（LMM）残差。

在Python中编写函数train()以封装多步神经网络的训练流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 模型训练 
def train(u_tensor, model, loss_func, h, M): 
    # 参数说明：训练集u_tensor,待训练模型model,损失函数loss_func,时间步长h,步数M,最大训练次数EPOCH
    optimizer = torch.optim.Adam(model.parameters(), lr=LR)
    loss_history = []
    
    for epoch in range(EPOCHS):          
        model.train()        
        batch_u = u_tensor.to(device)        
        train_loss = loss_func(batch_u, model, h, M)   
        optimizer.zero_grad()      
        train_loss.backward()    
        optimizer.step()    
        epoch_avg_loss = train_loss.item()         
        loss_history.append(epoch_avg_loss) 
    
    return loss_history

其中loss_func即为上述定义的均方误差损失函数MSE：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 损失函数
def loss_func(u, model, h, M):
	# 参数说明：模型输入数据u,待训练模型model,时间步长h,步数M

    # 根据选定的方法确定系数α、β（示例：Adams-Moulton法，M=4）
    alpha = [1, -1, 0, 0, 0]
    beta = [251/720, 646/720, -264/720, 106/720, -19/720]
        
    loss = 0.0
    for n in range(M, len(u)):
        residual = 0.0
        for m in range(M+1):
            u_nm = u[n - m].unsqueeze(0)
            f_nm = model(u_nm)
            residual += alpha[m] * u[n - m] + h * beta[m] * f_nm.squeeze()
        loss += torch.norm(residual) ** 2
    return loss / (len(u) - M + 1)

基于多步神经网络改进的常微分方程反演算法

改进的多步神经网络算法

多步神经网络做出了比较理想的假设，即给出了所有的数值解数据是无噪声的，以及神经网络可以表示对常微分方程产生零残差的反演。这种假设是理想化的，我们可以在实际情况下使用改进的方法尝试发现未知常微分方程。

对于多步神经网络，除线性多步法残差之外，如果神经网络能够满足一些通用近似性质，尤其是在多步神经网络反演法效果不佳的非自治常微分方程的反演问题中，可以扩展精确和完整数据的收敛结果。考虑到神经网络对函数近似的强大能力（见通用近似定理），这意味着至少在合适的光滑的常微分方程中存在良好的泛化误差。

假设数据集为给定在若干时刻t_1、t_2、…、t_N的方程的数值解u的值，把每一时刻t_n对应的解u(t_n)记为u^(n)，而t_n对应的导数数据一般无从得知。当时间间隔h较小时，可用二阶中心差分法近似求出导数数据，记对于每一时刻t_n求出的导数数据为d^(n)，则：
$$
d^{(n)}=\begin{cases}(-3\boldsymbol{u}^{(n)}+4\boldsymbol{u}^{(n+1)}-\boldsymbol{u}^{(n+2)})/2h,\quad n=1,\(\boldsymbol{u}^{(n+1)}-\boldsymbol{u}^{(n-1)})/2h,\quad1<n<N,\(\boldsymbol{u}^{(n-2)}-4\boldsymbol{u}^{(n-1)}+3\boldsymbol{u}^{(n)})/2h,\quad n=N.&\end{cases}
$$
显然二阶中心差分法求导数d^(n)的误差为o(h^2)。

对于常微分方程的反演，我们改进了多步神经网络的损失函数，其中既包含解数据，又包含导数数据：
$$
L=l_1(u,d)+l_2(u,d,f_{NN})
$$
其中：
$$
l_{1}=\frac{1}{N-M+1}\sum_{n=M}^{N}\left|\sum_{m=0}^{M}[\alpha_{m}u_{n-m}+h\beta_{m}f_{NN}(u_{n-m})]\right|^{2}
$$

$$
l_{2}=\frac{1}{N-M+1}\sum_{n=M}^{N}\left|f_{NN}(u_{n})-d_{n}\right|^{2}
$$

$$
n=M,\ldots,N
$$

式中向量范数采用二范数；u为数值解的数据，d为二阶中心差分法得到的导数数据，则有：

• l_1：线性多步法残差，可以表示常微分方程的近似程度
• l_2：均方误差函数，可以表示网络结构的准确度

把u^(n)作为输入，d^(n)作为期望输出进行训练，得到的f_NN即为对函数f的近似。训练流程与改进后的损失函数Python实现如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 模型训练 
def train(u_tensor, model, loss_func, h, M): 
    # 参数说明：训练集u_tensor,待训练模型model,损失函数loss_func,时间步长h,步数M,最大训练次数EPOCH
    optimizer = torch.optim.Adam(model.parameters(), lr=LR)
    loss_history = []
    
    for epoch in range(EPOCHS):
        model.train()
        batch_u = u_tensor.to(device)
        batch_d = d_tensor.to(device)
        train_loss = loss_func(batch_u, batch_d, model, h, M)
        optimizer.zero_grad()
        train_loss.backward()
        optimizer.step()
        epoch_avg_loss = train_loss.item()
        loss_history.append(epoch_avg_loss)
        
    return loss_history

可以看到，与改进前相比，在训练过程中增加了对二阶中心差分法得到的导数的相关计算，进一步利用了训练数据中的信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 损失函数
def loss_func(u, d, model, h, M):
    # 参数说明：模型输入数据u,输入数据对应的真实微分数据d,待训练模型model,时间步长h,步数M

    # 根据选定的方法确定系数α、β（示例：Adams-Moulton法，M=4）
    alpha = [1, -1, 0, 0, 0]
    beta = [251/720, 646/720, -264/720, 106/720, -19/720]
        
    # 多步法残差 l1
    l1 = 0.0
    for n in range(M, len(u)):
        residual = 0.0
        for m in range(M+1):
            u_nm = u[n - m].unsqueeze(0)
            f_nm = model(u_nm)
            residual += alpha[m] * u[n - m] + h * beta[m] * f_nm.squeeze()
        l1 += torch.norm(residual) ** 2
    l1 = l1 / (len(u) - M + 1)
    
    # 导数拟合误差 l2
    pred_d = model(u)
    l2 = torch.mean(torch.norm(pred_d - d, dim=1) ** 2)
    
    return l1 + l2  # 总损失

值得注意的是，针对非自治常微分方程，由于在将其变换为自治常微分方程时进行了升维操作，这意味着真实的导数向量在y=t这一分量上的值必然是1，因此后续在检验模型训练效果时可利用这一点对模型性能进行先决的把握。

基于误差界理论论证改进算法的优越性

在上述损失函数中，l_1是对目标函数的良好近似，而l_2是神经网络中常用的损失函数。考虑到神经网络对函数近似的强大能力，这意味着即使对于噪声数据，改进的方法也应有良好的泛化能力和鲁棒性。在这里，我们先从理论上来论证改进方法在泛化能力与鲁棒性上的优越性，后续的数值实验部分将采用三类非自治方程的反演来验证改进的多步神经网络的效果。

对于二分类问题（可推广至函数近似的回归问题），当假设空间是有限个函数的集合F={f_1,f_2,…,f_d}时，对任意一个函数f∈F,至少以概率1-δ，以下不等式成立：
$$
R(f)\leq\hat{R}(f)+\varepsilon(d,N,\delta)
$$
其中：
$$
\begin{gathered}R(f)=E[L(Y,f(X))]\\hat{R}(f)=\frac{1}{N}\sum_{1}^{N}L(y_{i},f(x_{i}))\\varepsilon(d,N,\delta)=\sqrt{\frac{1}{2N}(\log d+\log\frac{1}{\delta})}\end{gathered}
$$
式中，R(f)为泛化误差（测试集上的测试风险），\hat{R}(f)为训练集上的经验风险，\hat{R}(f) + ε(d,N,δ)即为泛化误差界。观察上式可知，泛化误差界与样本数N成正比，与假设空间包含的函数数量d成反比。因此，当样本数N越大，泛化误差界越小，当假设空间F包含的函数越多，泛化误差界越大。

根据上述定理，针对改进后的神经网络，有如下不等式成立：
$$
\left|f_{NN}(u^{(n)})-\hat{f}(u^{(n)})\right|\leq\left|f_{NN}(u^{(n)})-d^{(n)}\right|+\left|\hat{f}(u^{(n)})-d^{(n)}\right|\leq w+o(h^{2})
$$
该不等式表明，改进后的损失函数可以拆解成两部分误差：

• 第一部分为通过神经网络得到的导数近似值与通过二阶中心差分法求出的导数之间的误差，设该误差限为w；
• 第二部分为导数真实值与通过二阶中心差分法求出的导数之间的误差，根据二阶中心差分法的基本原理，其误差限为**o(h^2)**。

显然改进后的多步神经网络的泛化误差相较改进前有了进一步的约束，尤其显著减小了噪声对模型的影响，具有更强的泛化能力和鲁棒性。

数值实验与分析

为充分验证改进方法的泛化能力与鲁棒性，我们选取了六个实际的物理问题（对应常微分方程）作为测试用例，对应自治/非自治以及三种不同的线性多步法，在每一个测试用例内选取不同的线性多步法步数以及训练数据所含的高斯噪声方差，对改进前后的两种基于多步神经网络的常微分方程反演方法进行测试。下面我们以“受迫振动方程”这一用例详细展示测试流程，其他的测试用例仅作结果展示。

数值实验流程

数据构建

基于选定的测试用例对应的常微分方程，可采用如下步骤生成原始的真实数据集：

1. 在所给区域内均匀选取间隔为h的N个结点t_n,n=1,2,…,N ,使用Python中的Scipy库求出各结点对应的数值解u^(n)；
2. 将数值解u^(n) 代入二阶中心差分法中得到每个x_n 对应的导数值d^(n) ；
3. 噪声数据构建：在各结点对应的数值解u^(n) 上依次加上期望为0，方差为0、0.01、0.05的高斯噪声。

在Python中，用函数get_data()函数实现了数据构建的代码封装：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

def get_data(t0, t_end, h, y0, noise_std=0.0):     
    t_eval = np.arange(t0, t_end + h, h)     
    
    # 数值解    
    sol = solve_ivp(forced_oscillator, [t0, t_end], y0, t_eval=t_eval)    
    x = sol.y.T  # shape: [N, 2]     
    t = sol.t.reshape(-1, 1)  # shape: [N, 1]     
    
    # 添加高斯噪声     
    if noise_std > 0:         
        x += np.random.normal(0, noise_std, size=x.shape)      
        
    # 构造 u = [x1, x2, t]     
    u = np.hstack([x, t])      
    
    # 二阶中心差分求导数 d ≈ du/dt     
    d = np.zeros_like(u)     
    # 边界点使用前向/后向差分     
    d[0] = (-3 * u[0] + 4 * u[1] - u[2]) / (2 * h)     
    d[-1] = (u[-3] - 4 * u[-2] + 3 * u[-1]) / (2 * h)     
    # 内部点使用中心差分     
    d[1:-1] = (u[2:] - u[:-2]) / (2 * h)      
    
    u_tensor = torch.tensor(u, dtype=torch.float32)     
    d_tensor = torch.tensor(d, dtype=torch.float32)      
    
    return u_tensor, d_tensor, t# 模型训练 

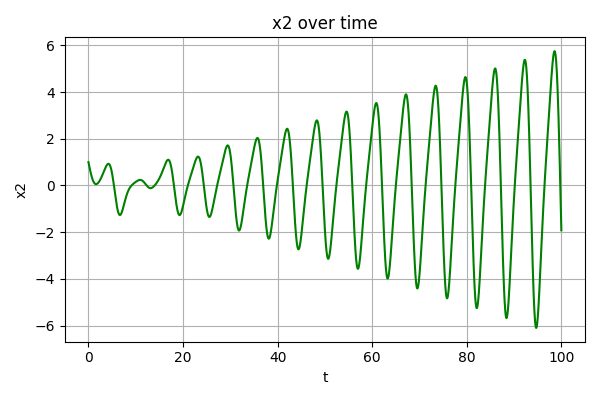
以“受迫振动方程”这一测试框架为例，force_oscillator函数中刻画了该场景下的微分方程规律：

1
2
3
4
5

def forced_oscillator(t, y):
    x1, x2 = y
    dx1dt = x2
    dx2dt = -np.cos(t) * x1 - x2 + t / 50
    return [dx1dt, dx2dt]

生成的无噪声数据如下图所示：

神经网络训练

根据上述算法理论部分列出的训练流程框架，适用数据（u，d）对神经网络进行训练，训练后得到的函数f_NN即为对函数f的近似。

关于神经网络的结构与参数，本项目中所使用的神经网络结构均相同（后续不再赘述），均包含4个隐藏层，每层128个神经元，激活函数为tanh，Python中基于pytorch框架对神经网络架构的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import torch.nn as nn

class ODEApproximator(nn.Module):
    def __init__(self, input_dim=3, hidden_dim=128, output_dim=3):
        super(ODEApproximator, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, output_dim)
        )

    def forward(self, x):
        return self.net(x)

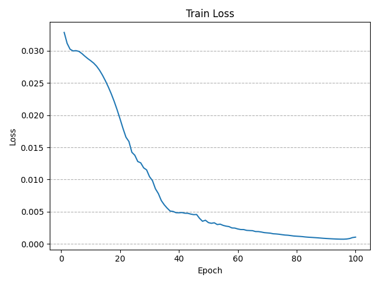
训练过程中实时记录了每一个epoch的损失函数值，下图分别绘制了改进前后的多步神经网络在无噪声数据集上训练过程中损失函数值的变化情况（总Epoch=100），可以看到损失函数均呈收敛态势，且改进后的多步神经网络收敛更快：

效果检验

为定量地比较改进前后的多步神经网络的泛化性能与鲁棒性，采取如下的实验步骤进行训练后模型的效果检验：

1. 用训练得到的函数f_NN解方程得到数值解u_NN^(n) ,观察近似效果，计算均方误差mse_x 和平均绝对误差mae_x并与多步神经网络作比较；
2. 用数值解u^(n)代入训练得到的函数f_NN得到的导数的近似值d_NN^(n)，将u^(n)代入给定的常微分方程中的 f 得到导数的真实值d^(n),计算均方误差mse_f和平均绝对误差mae_f并与多步神经网络作比较。

其中用于比较性能的指标均方误差mse和平均绝对误差mae的定义式如下所示：
$$
mse_{x}=\frac{1}{ND}\sum_{n=1}^{N}\left|u_{NN}^{(n)}-u^{(n)}\right|_{2}^{2}
$$

$$
mse_{f}=\frac{1}{ND}\sum_{n=1}^{N}\left|d_{NN}^{(n)}-d^{(n)}\right|_{2}^{2}
$$

$$
mae_{x}=\frac{1}{ND}\sum_{n=1}^{N}\left|u_{NN}^{(n)}-u^{(n)}\right|_{1}
$$

$$
mae_{f}=\frac{1}{ND}\sum_{n=1}^{N}\left|d_{NN}^{(n)}-d^{(n)}\right|_{1}
$$

Python中将利用训练好的模型进行预测的过程封装成函数predict_u，指标计算直接调用scikit-learn函数库中的相关函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def rhs(t, u_np):      
    """用于 solve_ivp：输入 u = [x1, x2, t] 输出 du/dt"""      
    u_tensor = torch.tensor(u_np, dtype=torch.float32).unsqueeze(0).to(device)      
    with torch.no_grad():          
        du_dt = model(u_tensor).squeeze().cpu().numpy()      
    return du_dt    

def predict_u(u_tensor):      
    # 初始条件与时间点一致     
    u0 = u_tensor[0].cpu().numpy()  # [x1, x2, t]    
    t_span = (0, 100)  
    t_eval = np.arange(0, 100 + 0.05, 0.05)    
    
    sol_nn = solve_ivp(rhs, t_span, u0, t_eval=t_eval)   
    return sol_nn.y.T  # shape: [N, 3]

在“受迫振动方程”这一测试案例中，基于训练轮数Epoch=50的模型，运行以上检验流程，得到如下检验指标数据：

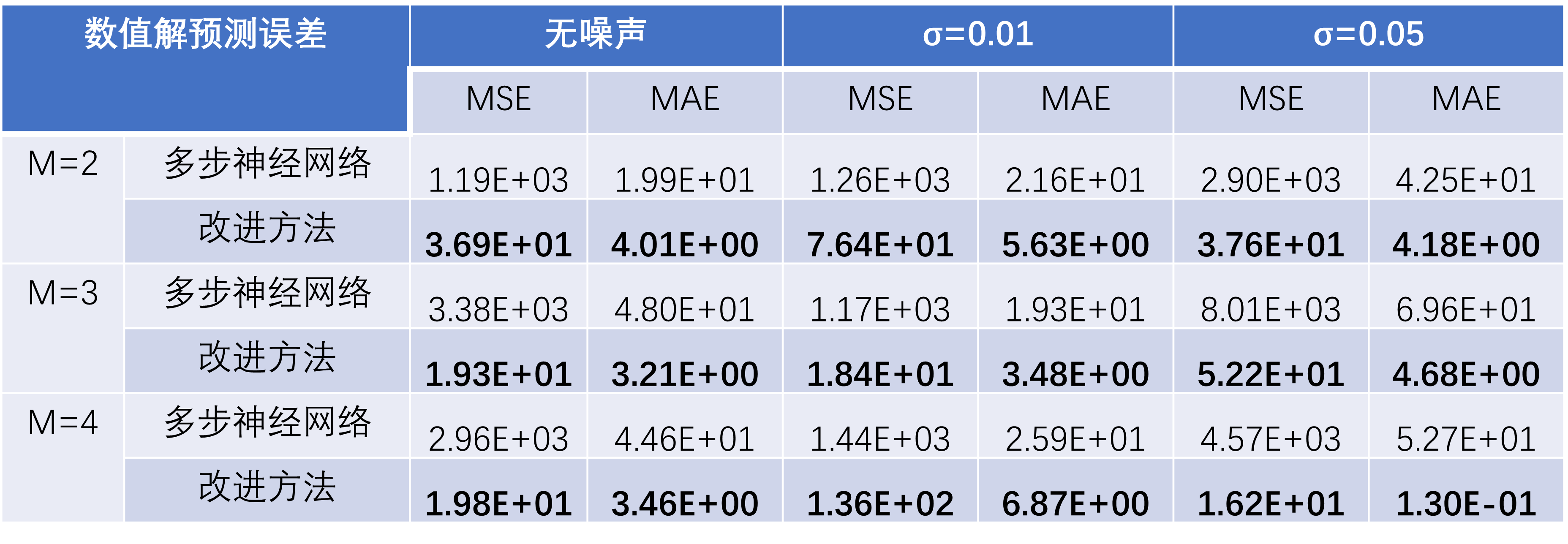
可以看到，随着噪声强度增加，两种方法的误差均增大，但改进方法对数值解的预测误差在各种情况下均小于多步神经网络。

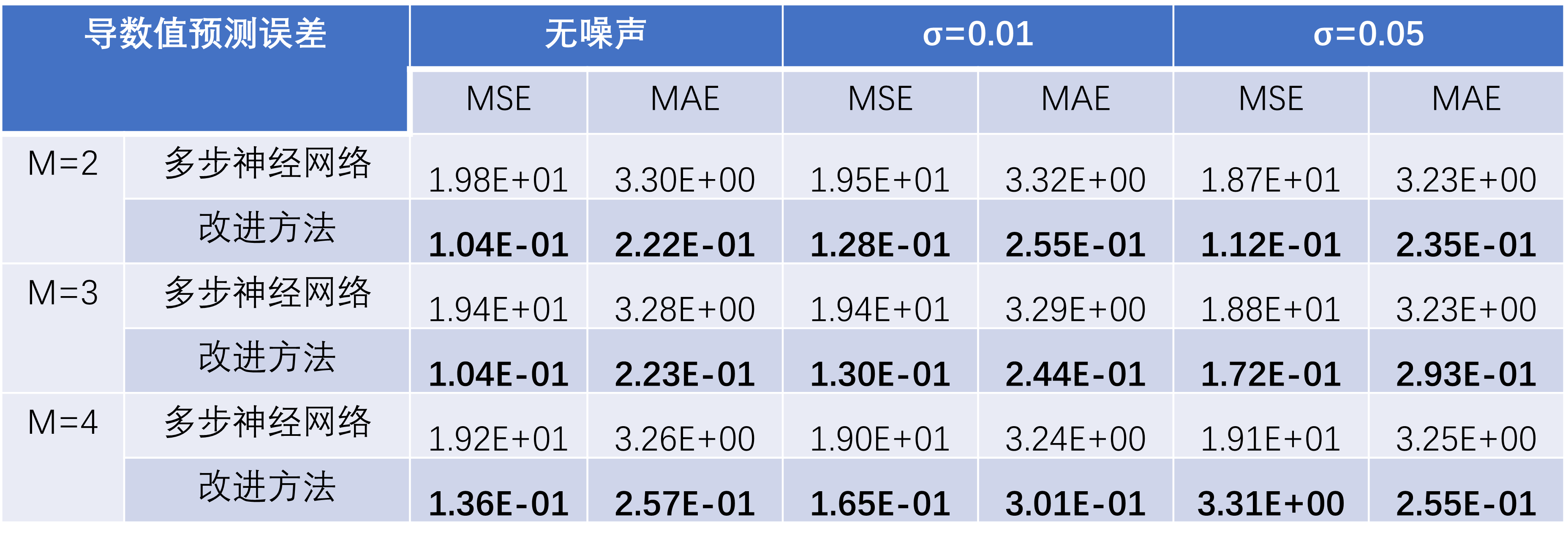
可以看到，当数据无噪声时，本文提出的改进方法对于受迫振动方程的近似效果强于多步神经网络;随着噪声强度的增加，多步神经网络的误差大幅增加，而改进的方法的误差一直保持较小且始终强于多步神经网络。

除此之外，针对在无噪声数据集上训练轮数分别为Epoch=100和Epoch=500时的模型，将其作为微分方程中的f用于预测数据的生成，效果分别如下图所示：

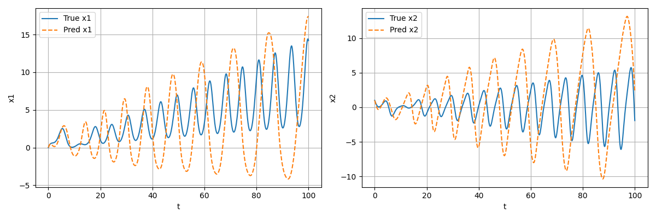
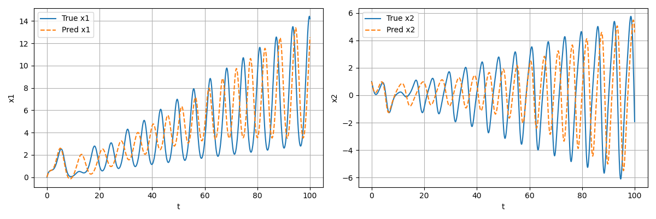
可以看到，随着训练轮数的增加，模型对于实际微分方程的拟合效果越来越好，生成的预测数据也越来越接近用于训练的真实数据；事实上，从理论上讲，大概在训练轮数Epoch达到10^4数量级时才会有较为精准的拟合效果，本项目由于用于训练的计算资源有限，仅进行了最大训练轮数为1000的测试。在后续的结果分析部分，将直接采用高训练轮数下的精确结果进行展示。

数值实验结果分析

非自治常微分方程

受迫振动方程——Adams-Moulton法

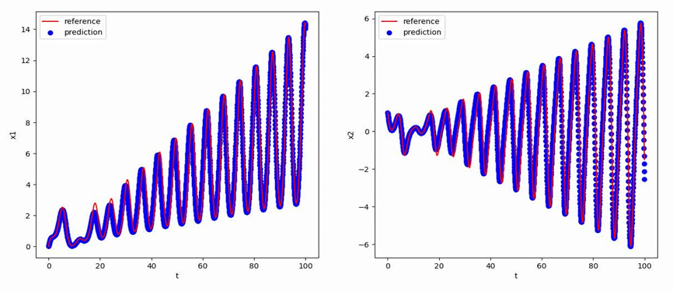
受迫振动方程(Forced Oscillator)是描述一个振动系统在外界力的作用下进行振动的方程。这个方程可以用来研究各种物理系统中的振动现象，例如弹簧振子、摆锤、电路振荡等。受迫振动方程的核心思想是将外界力引入方程中，以描述振动系统在外界激励下的行为。受迫振动方程的研究对于科学、工程和技术领域具有重要意义。它不仅有助于我们深入理解振动现象的本质和规律，还为我们设计和优化振动控制系统、减振装置等提供了理论基础。同时，它在电子设备、结构工程、交通运输等方面也有广泛的应用。

实验使用的受迫振动方程如下：
$$
\begin{aligned}&\frac{dx_1}{dt}=x_2,\&\frac{dx_2}{dt}=-cosy\cdot x_1-x_2+\frac{y}{50},\&\frac{dy}{dt}=1\end{aligned}
$$
使用[0,1,0]T作为初值，生成从t=0到t=100，间隔h=0.05的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

线性标量方程——Adams-Bashforth法

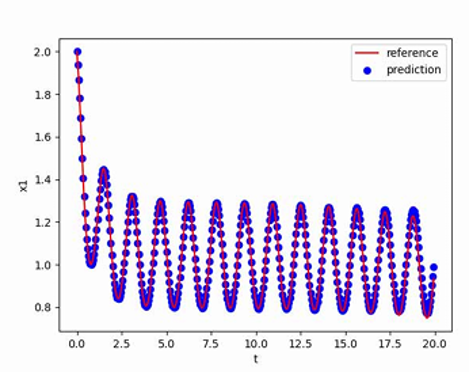
线性标量方程(Linear Scalar Equation)是一种描述某个未知函数与其导数之间的关系的方程，其中未知函数的导数的最高次数为1。线性标量方程是微分方程中的一类重要问题，它在数学物理等领域中有广泛应用。线性标量方程的研究对于数学、物理学和工程学等领域具有重要意义。它可以用来描述动力学系统的行为、传热和传质过程、量子力学中的波函数演化等。通过分析和求解线性标量方程，可以深入理解系统的特征、稳定性、渐近行为等，为问题的模拟、控制和优化提供理论基础。在现代科学和工程中，线性标量方程的研究得到了进一步推广和延伸。例如，非线性标量方程、偏微分方程等是线性标量方程的扩展和推广，它们更好地描述了一些复杂的物理现象和现实问题。

实验使用的线性标量方程如下：
$$
\frac{dx_1}{dt}=-x_1(sin4y+1)+cos\frac{y^2}{1000},
$$

$$
\frac{dy}{dt}=1
$$

使用[2,0]T作为初值，生成从t=0到t=20，间隔h=0.05的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

食饵-捕食者模型方程——后向微分公式法

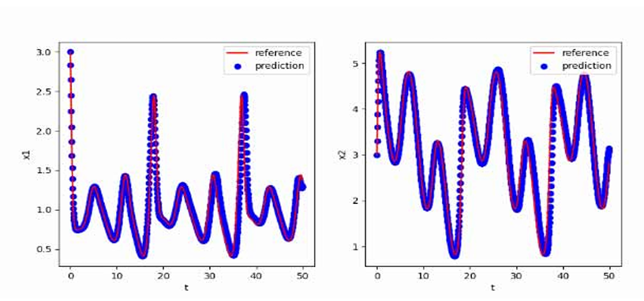
食饵-捕食者模型(Predator-prey Model)是生态学中研究食物链和生物群落动力学的重要模型之一，描述了食物链中食饵(被捕食者)和捕食者之间的相互作用关系。这种模型的研究对于我们理解生态系统的稳定性、物种相互作用以及生态系统中物种数量的变化具有重要意义。通过食饵-捕食者模型，我们可以研究食饵与捕食者之间的数量关系以及它们之间的相互作用。一般来说，食饵的数量被认为是捕食者的食物来源，并且捕食者的数量受到食饵的供给和捕食行为的影响。该模型通常描述了食饵数量随时间的变化，以及捕食者数量随时间的变化。食饵-捕食者模型的研究对于生态学、环境保护和资源管理等领域具有重要意义。通过该模型，我们可以深入了解生态系统中物种数量的变化规律，从而预测物种灭绝和生态系统崩溃的风险，以及寻找保护和管理生物多样性的方法。

实验使用的食饵-捕食者模型方程如下：
$$
\begin{aligned}&\frac{dx_1}{dt}=x_1-x_1\cdot x_2+sin\frac{y}{2}+cosy+2,\&\frac{dx_2}{dt}=x_1\cdot x_2-x_2,\&\frac{dy}{dt}=1\end{aligned}
$$
使用[3,3,0]T作为初值，生成从t=0到t=50，间隔h=0.05的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

自治常微分方程

线性常微分方程——Adams-Moulton法

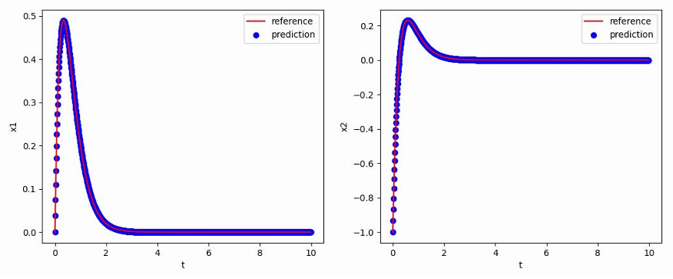
线性常微分方程(Linear ODEs)是微分方程中的一类重要问题，它描述了未知函数及其导数之间的线性关系。线性常微分方程的研究对于数学、物理学和工程学等领域具有重要意义。它们出现在物理学中许多基础问题的数学描述中，例如弹簧振动、电路分析、传热过程等。在工程学中，线性常微分方程也广泛应用于控制系统的建模和分析。随着科学技术的发展，研究者提出了各种各样的数值方法和近似方法，以求解复杂的线性常微分方程。这些方法包括欧拉方法、龙格-库塔方法、有限差分方法、变分法等，它们为实际问题的求解提供了有效的数值工具。随着对非线性动力学系统的研究和认识的深入，研究者们开始将非线性常微分方程引入到线性常微分方程中，以描述更为复杂的现象和现实问题。

实验使用的线性常微分方程如下：
$$
\frac{dx_1}{dt}=x_1-4x_2,
$$

$$
\frac{dx_2}{dt}=4x_1-7x_2
$$

使用[0,-1]T作为初值，生成从t=0到t=10，间隔h=0.01的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

阻尼三次振子方程——Adams-Bashforth法

阻尼三次振子(Damped Cubic Oscillator)是一种物理系统，它描述了受到阻尼力和弹力作用的振动系统。阻尼指的是系统中存在能量损耗的因素，如摩擦力，它会导致振动的逐渐减弱；三次振子表示系统的势能函数是一个三次函数，它具有非线性的特性。阻尼三次振子最早出现在振动力学和非线性动力学的研究中。对于振动系统的研究是物理学、工程学和应用数学等领域的重要课题之一。阻尼三次振子的研究对于理解和预测复杂动力学系统的行为具有重要意义。通过分析阻尼三次振子的运动规律和稳定性，我们可以深入了解非线性振动系统的动力学特性，例如振动的周期性、混沌行为等。这些研究也为控制系统、电子电路、力学系统等领域的工程应用提供了参考和启示。

实验使用的阻尼三次振子方程如下：
$$
\frac{dx_1}{dt}=-0.1x_1^3+2x_2^3,
$$

$$
\frac{dx_2}{dt}=-2x_1^3-0.1x_2^3
$$

使用[1,1]T作为初值，生成从t=0到t=25，间隔h=0.01的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

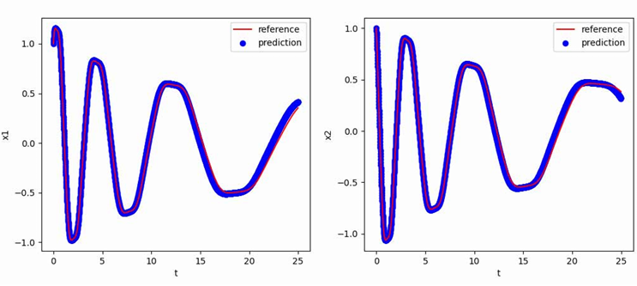
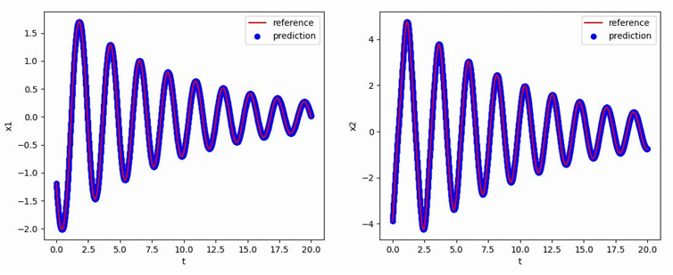
阻尼简谐摆方程——后向微分公式法

阻尼简谐摆(Damped Pendulum)是一个经典力学中的物理系统，它由一个具有质量的物体通过一根轻质绳或杆与一个固定支点相连接组成。阻尼简谐摆在受到重力作用下，沿着一条弧线进行周期性振动。阻尼简谐摆的研究对于理解和预测振动系统的行为具有重要意义。通过分析阻尼简谐摆的运动规律和稳定性，我们可以深入了解振动系统在存在阻尼时的响应特性，例如振动的振幅、频率等。这些研究不仅在理论物理学中具有重要意义，也为工程学中的控制系统、机械振动和结构动力学等领域的应用提供了基础。

实验使用的阻尼简谐摆方程如下：
$$
\begin{aligned}&\frac{dx_1}{dt}=x_2,\&\frac{dx_2}{dt}=-\alpha x_2-\beta\sin x_1,\&\alpha=0.2,\beta=8.91\end{aligned}
$$
使用[-1.193,-3.876]T作为初值，生成从t=0到t=20，间隔h=0.01的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

研究结论与创新

研究结论

本项目针对常微分方程的反演问题提出了一种基于多步神经网络改进的常微分方程反演算法，旨在从数据中提取内含的常微分方程。通过将导数数据融入训练数据，我们改进了多步神经网络的数据集，并优化了神经网络的损失函数，以提高模型的准确性和泛化能力。经过训练，改进的神经网络成功拟合原方程中的函数，实现了对非自治常微分方程的反演。我们还推导并讨论了改进算法的误差界。我们进一步将改进的算法应用于自治常微分方程反演，通过训练网络拟合原方程函数，拓展了算法在自治常微分方程反演中的适用性。

本项目通过实验以非自治常微分方程中的受迫振动方程、线性标量方程和食饵-捕食者模型方程，以及自治常微分方程中的线性常微分方程、阻尼三次振子方程和阻尼简谐摆方程为例，展示了算法的有效性。在实验中，我们添加了不同强度的噪声，并利用改进算法对常微分方程进行反演。实验结果表明，改进方法在大多数情况下优于多步神经网络，在处理有噪声数据时表现更为出色。这些结果充分验证了本文提出的方法在反演问题中的可行性和优越性。

研究方法创新性

传统方法通常利用多步神经网络来处理常微分方程的反演问题，主要集中在处理自治常微分方程，对于非自治常微分方程的反演效果不尽理想，特别是在使用带有噪声数据进行训练时表现不佳。本研究首次将研究重点聚焦于非自治常微分方程的反演，通过将非自治方程转化为自治方程的形式，提出了一种新的研究思路。针对带有噪声数据的方程反演问题，采用了改进损失函数的方法以提升算法的鲁棒性。此外，将这种新方法扩展应用于自治常微分方程的反演问题，结果显示其反演效果明显优于多步神经网络。这一新思路对解决常微分方程反演问题带来了一种新的方法。

参考文献

[1] 王开荣,杨大地编著.应用数值分析[M].高等教育出版社,2010.

[2] 付长铠.常微分方程反演的机器学习方法研究[D].长春工业大学,2024.

[3] Raissi M, Perdikaris P, Karniadakis G E. Multistep neural networks for data-driven discovery of nonlinear dynamical systems[J]. arXiv preprint arXiv:1801.01236, 2018.

[4] 李航. 统计学习方法[M]. 第二版. 北京：清华大学出版社, 2019.

[5] 陈新海, 刘杰, 万仟, 等. 一种改进的基于深度神经网络的偏微分方程求解方法[J]. 计算机工程与科学, 2022, 44(11): 1932-1940.

研究背景及其意义

图像放大与旋转是数字图像处理中最基础的几何变换操作，其核心在于如何通过插值算法重建原始图像中不存在的像素信息。当对图像进行放大操作时，输出图像的像素网格会超出原始图像的采样范围，需要通过插值来填补这些新增像素点的颜色值；而在旋转操作中，即使保持图像尺寸不变，原始像素的整数坐标经过旋转变换后也会落在新图像的非整数位置，同样需要通过插值来重新确定每个输出像素的颜色值。

图像插值是利用原图像中的颜色值通过一定的方法计算出待插入像素点的颜色值的过程。对图像进行插值一般有两个步骤：首先定义一个图像插值公式，然后利用该插值公式计算待插入点的颜色值。常见的图像插值算法有双线性法、最近邻法、非均匀法、双三次卷积插值法、双立方法、Lagrange法、 样条插值法、 克里金（Krijing） 插值法等。这些插值方法通常定义一个插值数据点的隐式函数，再提取该函数的等值面作为图像插值方法，常用的插值核包括线性插值核、样条插值核等。

• 最近邻插值作为最简单的算法，直接将距离待插值点最近的已知像素值作为结果，虽然计算效率极高（时间复杂度O(1)），但会产生明显的块状伪影（“马赛克”）和锯齿形边缘；
• 双线性插值通过考虑2×2邻域内四个像素的加权平均，在计算成本（O(n)）和视觉效果之间取得平衡，但仍会导致高频信息丢失和边缘模糊；
• 更高阶的双三次插值（使用4×4邻域）和样条插值虽然能提供更平滑的结果，但计算复杂度显著增加（O(n²)），且可能引入不必要的振铃效应。

现有算法的根本局限在于采用统一的插值核函数处理整幅图像，忽视了图像不同区域的特征差异。例如，在平坦区域使用复杂插值会造成计算资源浪费，而在纹理丰富区域使用简单插值又会导致细节损失。基于此，我们希望通过改良的四平面插值算法对图像的放大与旋转效果进行优化，根据图像局部特征自适应地选择不同的插值策略，以规避用同一个插值公式对所有像素进行插值存在的不足。

常用图像插值算法

课本在6.5节中提到，在插值节点数量较多时，为避免Runge振荡现象的发生，并不提倡用高次多项式进行插值，而宁可用低次多项式作分段插值。在图像处理这一特定的应用场景中，需要处理的图像尺寸规模往往较大，且同一行（列）的所有像素颜色值显然并不具有可以用一个多项式函数显式表达的规律，但相邻的像素点颜色值之间又存在一定的关联性，因此分段插值仅考虑局部特征的特性在这里能够良好地契合所需性能。根据对于待插入像素点周围已有的像素点信息的利用情况，这里列举了几种常见的图像插值算法：

• 最近邻法：仅利用待插值像素点转换至原图像坐标后距离其最近的一个像素点的颜色值，将其直接作为待插值像素点的颜色值
• 双线性法：利用待插值像素点转换至原图像坐标后距离其最近的四个像素点的颜色值，加权平均后作为待插值像素点的颜色值
• 双立方法：利用待插值像素点转换至原图像坐标后距离其最近的十六个像素点的颜色值，加权平均后作为待插值像素点的颜色值

最近邻法

如上图所示，在一维最近邻插值中，坐标轴上各点 xi-1，xi，xi+1 … 两两对半等分间隔 (红色虚线划分)，从而非边界的各坐标点都有一个等宽的邻域，并根据每个坐标点的值构成一个类似分段函数的函数约束，从而使各插值坐标点的值等同于所在邻域原坐标点的值。例如，插值点 x 坐落于 坐标点 xi 的邻域，那么其值 f(x) 就等于 f(xi)。

在二维的图像插值场景中，可以对上述一维最近邻插值进行推广，如下图所示：

可以看到，(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) 都是原图像上的坐标点，颜色值分别对应为 Q11、Q12、Q21、Q22。而颜色值未知的插值点 (x, y)（需转换至原图像坐标），根据最近邻插值方法的约束，其与坐标点 (x0, y0) 位置最接近 (即位于 (x0, y0) 的邻域内)，故插值点 (x, y) 的颜色值 P = Q11。

总而言之，最近邻法的基本思想即：将待插入点的坐标进行四舍五入，再以该行列坐标都是整数点的颜色值（灰度值）替代待插入点(x, y)处的颜色值。事实上，这也正是机器学习中KNN（K-Nearest Neighbor）算法在K=1时的情形。

基于以上算法思想，编写python函数代码实现图像放缩与旋转过程中的最近邻法插值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# 最近邻法插值实现图像放缩
def nearest_neighbor_interpolation(image, scale_factor):
    h, w, channel = image.shape
    new_h, new_w = int(h * scale_factor), int(w * scale_factor)
    resized_image = np.zeros((new_h, new_w, int(channel)), dtype=image.dtype)
    
    for i in range(new_h):
        for j in range(new_w):
            src_i = int(round((i + 1) / scale_factor, 0))
            src_j = int(round((j + 1) / scale_factor, 0))
            resized_image[i, j] = image[src_i - 1, src_j - 1]
    
    return resized_image

# 最近邻法插值实现图像旋转
def nearest_neighbor_rotation(image, angle):
    h, w, channel = image.shape
    angle_rad = math.radians(angle)
    
    # 计算旋转后的图像尺寸
    cos_theta = abs(math.cos(angle_rad))
    sin_theta = abs(math.sin(angle_rad))
    new_w = int(h * sin_theta + w * cos_theta)
    new_h = int(h * cos_theta + w * sin_theta)
    
    # 旋转中心
    cx, cy = w / 2, h / 2
    new_cx, new_cy = new_w / 2, new_h / 2
    
    rotated_image = np.zeros((new_h, new_w, channel), dtype=image.dtype)
    
    for i in range(new_h):
        for j in range(new_w):
            # 将新图像坐标转换回原图像坐标
            x = (j - new_cx) * math.cos(angle_rad) + (i - new_cy) * math.sin(angle_rad) + cx
            y = -(j - new_cx) * math.sin(angle_rad) + (i - new_cy) * math.cos(angle_rad) + cy
            
            # 最近邻插值
            if 0 <= x < w and 0 <= y < h:
                src_x = int(round(x))
                src_y = int(round(y))
                rotated_image[i, j] = image[src_y - 1, src_x - 1]
    
    return rotated_image

双线性法

如上图所示，在一维的线性插值中，坐标轴上各点 xi-1，xi，xi+1 … 的值“两两直接相连”为线段，从而构成了一条连续的约束函数。而插值坐标点例如 x，根据约束函数其值应为 f(x)。因为每两个坐标点之间的约束函数曲线是一次线性的线段，对插值结果而言是“线性” 的，所以该方法称为线性插值。基于线性函数的特性，可以便捷地求取原图像上的两个像素点间任一待插值点的颜色值：

可以看到，图中 x0 和 x1 都是原有的坐标点，颜色值分别对应为 y0 和 y1，此时根据线性插值法约束，在 (x0, y0) 和 (x1, y1) 构成的一次函数上，颜色值未知的插值点 x的颜色值 y 即为：
$$
y=y_0+(x-x_0)\frac{y_1-y_0}{x_1-x_0}=y_0+\frac{(x-x_0)y_1-(x-x_0)y_0}{x_1-x_0}
$$
实际上，即便 x 不在 x0 与 x1 之间，该公式也成立（此时为线性外插），但图像处理中不需涉及此情形。

从一维的线性插值出发，很容易拓展到二维图像的双线性插值，通过三次一阶线性插值（本质为加权求和）获得最终结果，下图便展示了该过程的定性斜视与定量俯视示意图：

其中，(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) 均为原图像上的像素坐标点，颜色值分别对应为 f(x0, y0)、f(x0, y1)、f(x1, y0)、f(x1, y1)。而颜色值未知的插值点 (x, y)，根据双线性插值法的约束，可以先由像素坐标点 (x0, y0) 和 (x0, y1) 在 y 轴向作一维线性插值得到 f(x0, y)、由像素坐标点 (x1, y0) 和 (x1, y1) 在 y 轴向作一维线性插值得到 f(x1, y)，然后再由 (x0, y) 和 (x1, y) 在 x 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y)。

事实上，一维线性插值先作 x 轴向再作 y 轴向，得到的结果完全相同，仅为顺序先后的区别。这里不妨先由像素坐标点 (x0, y0) 和 (x1, y0) 在 x 轴向作一维线性插值得到 f(x, y0)、由像素坐标点 (x0, y1) 和 (x1, y1) 在 x 轴向作一维线性插值得到 f(x, y1)：
$$
f(x,y_0)=\frac{x_1-x}{x_1-x_0}f(x_0,y_0)+\frac{x-x_0}{x_1-x_0}f(x_1,y_0)
$$

$$
f(x,y_1)=\frac{x_1-x}{x_1-x_0}f(x_0,y_1)+\frac{x-x_0}{x_1-x_0}f(x_1,y_1)
$$

然后再由 (x, y0) 和 (x, y1) 在 y 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y)：
$$
f(x,y)=\frac{y_1-y}{y_1-y_0}f(x,y_0)+\frac{y-y_0}{y_1-y_0}f(x,y_1)
$$
合并上述式子，得到最终的双线性插值结果：
$$
f(x,y)=\frac{(y_1-y)(x_1-x)}{(y_1-y_0)(x_1-x_0)}f(x_0,y_0)+\frac{(y_1-y)(x-x_0)}{(y_1-y_0)(x_1-x_0)}f(x_1,y_0)+\frac{(y-y_0)(x_1-x)}{(y_1-y_0)(x_1-x_0)}f(x_0,y_1)+\frac{(y-y_0)(x-x_0)}{(y_1-y_0)(x_1-x_0)}
$$
值得注意的是，在实际的图像插值处理过程中，为尽量保证插值效果的准确性，往往仅采用距离待插值点（转换至原图像坐标）最近的四个点，即:（[]符号表示待插值点转换至原图像坐标后向下取整）
$$
x_0=[x]，y_0=[y]
$$

$$
x_1=x_0+1，y_1=y_0+1
$$

从加权求和的角度理解，可以进一步地将双线性插值结果改写为如下形式：
$$
p=x-[x], q=y-[y]
$$

$$
\begin{array}{rcl}f(x,y)=(1-q){(1-p)f([x][y])+pf([x]+1,[y])}+q{(1-p)f([x],[y]+1)+pf([x]+1,[y]+1)}\end{array}
$$

基于以上算法思想，编写python函数代码实现图像放缩与旋转过程中的双线性法插值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

# 双线性法插值实现图像放缩
def bilinear_interpolation(image, scale_factor):
    h, w, channel = image.shape
    new_h, new_w = int(h * scale_factor), int(w * scale_factor)
    resized_image = np.zeros((new_h, new_w, int(channel)), dtype=image.dtype)
    
    for i in range(new_h):
        for j in range(new_w):
            x = (j + 1) / scale_factor
            y = (i + 1) / scale_factor
            x1 = int(x)
            y1 = int(y)
            x2 = x1 + 1
            y2 = y1 + 1
            p = x - x1
            q = y - y1

            # 边界问题处理
            if x2 == w + 1:
                x2 = x1
            if y2 == h + 1:
                y2 = y1
                
            resized_image[i ,j] = (1 - q) * ((1 - p) * image[y1 - 1, x1 - 1] + p * image[y1 - 1, x2 - 1]) + q * ((1 - p) * image[y2 - 1, x1 - 1] + p * image[y2 - 1, x2 - 1])
    
    return resized_image

# 双线性法插值实现图像旋转
def bilinear_rotation(image, angle):
    h, w, channel = image.shape
    angle_rad = math.radians(angle)
    
    # 计算旋转后的图像尺寸
    cos_theta = abs(math.cos(angle_rad))
    sin_theta = abs(math.sin(angle_rad))
    new_w = int(h * sin_theta + w * cos_theta)
    new_h = int(h * cos_theta + w * sin_theta)
    
    # 旋转中心
    cx, cy = w / 2, h / 2
    new_cx, new_cy = new_w / 2, new_h / 2
    
    rotated_image = np.zeros((new_h, new_w, channel), dtype=image.dtype)
    
    for i in range(new_h):
        for j in range(new_w):
            # 将新图像坐标转换回原图像坐标
            x = (j - new_cx) * math.cos(angle_rad) + (i - new_cy) * math.sin(angle_rad) + cx
            y = -(j - new_cx) * math.sin(angle_rad) + (i - new_cy) * math.cos(angle_rad) + cy
            
            # 双线性插值
            if 0 <= x < w-1 and 0 <= y < h-1:
                x1, y1 = int(x), int(y)
                x2, y2 = min(x1 + 1, w - 1), min(y1 + 1, h - 1)
                
                # 计算权重
                a = x - x1
                b = y - y1
                
                # 边界处理
                if x2 >= w:
                    x2 = x1
                if y2 >= h:
                    y2 = y1
                
                # 插值计算
                rotated_image[i, j] = (1 - a) * (1 - b) * image[y1, x1] + \
                                     a * (1 - b) * image[y1, x2] + \
                                     (1 - a) * b * image[y2, x1] + \
                                     a * b * image[y2, x2]
    
    return rotated_image    

双立方法

双立方法插值又称立方卷积插值/双三次插值，这也是数值分析中最常用的二维插值方法。在这种方法中，插值点 (x, y) 的像素颜色值 f(x, y) 通过矩形网格中最近的十六个采样点的加权平均得到，而各采样点的权重由该点到待求插值点的距离确定，此距离包括水平和竖直两个方向上的距离。相比之下，双线性插值仅由周围的四个采样点加权得到。

如上图所示，设（转换至原图像中）待求插值点坐标为 (i+u, j+v)【i、j为整数部分，u、v为小数部分】，已知其周围的 16 个像素坐标点 (网格) 的颜色值，还需要计算 16 个点各自的权重。以像素坐标点 (i, j) 为例，因为该点在 y 轴和 x 轴方向上与待求插值点 (i+u, j+v) 的距离分别为 u 和 v，所以其权重为 w(u) × w(v)，其中 w(·) 是插值权重核 (可以理解为定义的权重函数)。同理可得其余 15 个像素坐标点各自的权重。那么，待求插值点 (i+u, j+v) 的颜色值 f(i+u, j+v) 将通过如下计算得到：
$$
f(i+u,j+v)=A\times B\times C
$$
其中各项由向量或矩阵表示为：
$$
\mathrm{A}=[w(1+u)w(u)w(1-u)w(2-u)]
$$

$$
\mathrm{B}=\begin{bmatrix}f(i-1,j-1)&f(i-1,j+0)&f(i-1,j+1)&f(i-1,j+2)\f(i+0,j-1)&f(i+0,j+0)&f(i+0,j+1)&f(i+0,j+2)\f(i+1,j-1)&f(i+1,j+0)&f(i+1,j+1)&f(i+1,j+2)\f(i+2,j-1)&f(i+2,j+0)&f(i+2,j+1)&f(i+2,j+2)\end{bmatrix}
$$

$$
\mathbb{C}=[w(1+v)w(v)w(1-v)w(2-v)]^T
$$

插值权重核 w(·) 为：
$$
w(x)=\begin{cases}1-2|x|^2+|x|^3&,|x|<1\4-8|x|+5|x|^2-|x|^3&,1\leq|x|<2\0&,|x|\geq2&\end{cases}
$$
插值权重核 w(·) 的函数图像：

为方便后续算法实现，将以上加权求和过程各步骤展开，合并后化简得到待插入点的颜色值计算公式：
$$
f(i+u,j+v)=\sum_{m=0}^{3}\sum_{n=0}^{3}a_{mn}u^{m}v^{n}
$$
其中多项式的系数a_{mn}计算公式如下：(式中p {qr}与上述矩阵B中元素一一对应，如p 00=f(i-1,j-1))
$$
\begin{aligned}
&a{00}=p{11}\&a_{01}=-\frac{1}{2}p_{10}+\frac{1}{2}p_{12}\&a_{02}=p_{10}-\frac{5}{2}p_{11}+2p_{12}-\frac{1}{2}p_{13}\&a_{03}=-\frac{1}{2}p_{10}+\frac{3}{2}p_{11}-\frac{3}{2}p_{12}+\frac{1}{2}p_{13}\&a_{10}=-\frac{1}{2}p_{01}+\frac{1}{2}p_{21}\&a_{11}=\frac{1}{4}p_{00}-\frac{1}{4}p_{02}-\frac{1}{4}p_{20}+\frac{1}{4}p_{22}\&a_{12}=-\frac{1}{2}p_{00}+\frac{1}{4}p_{01}-p_{02}+\frac{1}{4}p_{03}+\frac{1}{2}p_{20}-\frac{5}{4}p_{21}+p_{22}-\frac{1}{4}p_{23}\&a_{13}=\frac{1}{4}p_{00}-\frac{3}{4}p_{01}+\frac{3}{4}p_{02}-\frac{1}{4}p_{03}-\frac{1}{4}p_{20}+\frac{3}{4}p_{21}-\frac{3}{4}p_{22}+\frac{1}{4}p_{23}\
&a_{20}=p_{01}-\frac{5}{2}p_{11}+2p_{21}-\frac{1}{2}p_{31}\
&a_{21}=-\frac{1}{2}p_{00}+\frac{1}{2}p_{02}+\frac{5}{4}p_{10}-\frac{5}{4}p_{12}-p_{20}+p_{22}+\frac{1}{4}p_{30}-\frac{1}{4}p_{32}\&a_{22}=p_{00}-\frac{5}{2}p_{01}+2p_{02}-\frac{1}{2}p_{03}-\frac{5}{2}p_{10}+\frac{25}{4}p_{11}-5p_{12}+\frac{5}{4}p_{13}+2p_{20}-5p_{21}+4p_{22}-p_{23}-\frac{1}{2}p_{30}+\frac{5}{4}p_{31}-p_{32}+\frac{1}{4}p_{33}\
&a_{23}=-\frac{1}{2}p_{00}+\frac{3}{2}p_{01}-\frac{3}{2}p_{02}+\frac{1}{2}p_{03}+\frac{5}{4}p_{10}-\frac{15}{4}p_{11}+\frac{15}{4}p_{12}-\frac{5}{4}p_{13}-p_{20}+3p_{21}-3p_{22}+p_{23}+\frac{1}{4}p_{30}-\frac{3}{4}p_{31}+\frac{3}{4}p_{32}-\frac{1}{4}p_{33}\
&a_{30}=-\frac{1}{2}p_{01}+\frac{3}{2}p_{11}-\frac{3}{2}p_{21}+\frac{1}{2}p_{31}\
&a_{31}=\frac{1}{4}p_{00}-\frac{1}{4}p_{02}-\frac{3}{4}p_{10}+\frac{3}{4}p_{12}+\frac{3}{4}p_{20}-\frac{3}{4}p_{22}-\frac{1}{4}p_{30}+\frac{1}{4}p_{32}\&a_{32}=-\frac{1}{2}p_{00}+\frac{5}{4}p_{01}-p_{02}+\frac{1}{4}p_{03}+\frac{3}{2}p_{10}-\frac{15}{4}p_{11}+3p_{12}-\frac{3}{4}p_{13}-\frac{3}{2}p_{20}+\frac{15}{4}p_{21}-3p_{22}+\frac{3}{4}p_{23}+\frac{1}{2}p_{30}-\frac{5}{4}p_{31}+p_{32}-\frac{1}{4}p_{33}\&a_{33}=\frac{1}{4}p_{00}-\frac{3}{4}p_{01}+\frac{3}{4}p_{02}-\frac{1}{4}p_{03}-\frac{3}{4}p_{10}+\frac{9}{4}p_{11}-\frac{9}{4}p_{12}+\frac{3}{4}p_{13}+\frac{3}{4}p_{20}-\frac{9}{4}p_{21}+\frac{9}{4}p_{22}-\frac{3}{4}p_{23}-\frac{1}{4}p_{30}+\frac{3}{4}p_{31}-\frac{3}{4}p_{32}+\frac{1}{4}p_{33}
\end{aligned}
$$
基于以上算法思想，编写python函数代码实现图像放缩与旋转过程中的双立方法插值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148

# 双立方法插值实现图像放缩
def bicubic_interpolation(image, scale_factor):
    h, w, channel = image.shape
    new_h, new_w = int(h * scale_factor), int(w * scale_factor)
    resized_image = np.zeros((new_h, new_w, channel))
    
    for i in range(new_h):
        for j in range(new_w):
            x = i / scale_factor
            y = j / scale_factor
            
            # 确定16个邻域像素的坐标
            x0 = max(0, int(np.floor(x)) - 1)
            x1 = x0 + 1
            x2 = x0 + 2
            x3 = min(w-1, x0 + 3)
            
            y0 = max(0, int(np.floor(y)) - 1)
            y1 = y0 + 1
            y2 = y0 + 2
            y3 = min(h-1, y0 + 3)
            
            # 获取16个邻域像素的值
            p = np.zeros((4, 4, 3))
            for m in range(4):
                for n in range(4):
                    xi = x0 + n
                    yi = y0 + m
                    xi = min(max(xi, 0), w-1)  # 边界处理
                    yi = min(max(yi, 0), h-1)
                    p[m, n] = image[yi, xi]
            
            # 计算相对位置
            dx = x - x1
            dy = y - y1

            # 系数
            a = np.zeros((4, 4, channel))
            a[0, 0] = p[1, 1]
            a[0, 1] = -0.5*p[1, 0] + 0.5*p[1, 2]
            a[0, 2] = p[1, 0] - 2.5*p[1, 1] + 2*p[1, 2] - 0.5*p[1, 3]
            a[0, 3] = -0.5*p[1, 0] + 1.5*p[1, 1] - 1.5*p[1, 2] + 0.5*p[1, 3]
            
            a[1, 0] = -0.5*p[0, 1] + 0.5*p[2, 1]
            a[1, 1] = 0.25*p[0, 0] - 0.25*p[0, 2] - 0.25*p[2, 0] + 0.25*p[2, 2]
            a[1, 2] = -0.5*p[0, 0] + 1.25*p[0, 1] - p[0, 2] + 0.25*p[0, 3] + 0.5*p[2, 0] - 1.25*p[2, 1] + p[2, 2] - 0.25*p[2, 3]
            a[1, 3] = 0.25*p[0, 0] - 0.75*p[0, 1] + 0.75*p[0, 2] - 0.25*p[0, 3] - 0.25*p[2, 0] + 0.75*p[2, 1] - 0.75*p[2, 2] + 0.25*p[2, 3]
            
            a[2, 0] = p[0, 1] - 2.5*p[1, 1] + 2*p[2, 1] - 0.5*p[3, 1]
            a[2, 1] = -0.5*p[0, 0] + 0.5*p[0, 2] + 1.25*p[1, 0] - 1.25*p[1, 2] - p[2, 0] + p[2, 2] + 0.25*p[3, 0] - 0.25*p[3, 2]
            a[2, 2] = p[0, 0] - 2.5*p[0, 1] + 2*p[0, 2] - 0.5*p[0, 3] - 2.5*p[1, 0] + 6.25*p[1, 1] - 5*p[1, 2] + 1.25*p[1, 3] + 2*p[2, 0] - 5*p[2, 1] + 4*p[2, 2] - p[2, 3] - 0.5*p[3, 0] + 1.25*p[3, 1] - p[3, 2] + 0.25*p[3, 3]
            a[2, 3] = -0.5*p[0, 0] + 1.5*p[0, 1] - 1.5*p[0, 2] + 0.5*p[0, 3] + 1.25*p[1, 0] - 3.75*p[1, 1] + 3.75*p[1, 2] - 1.25*p[1, 3] - p[2, 0] + 3*p[2, 1] - 3*p[2, 2] + p[2, 3] + 0.25*p[3, 0] - 0.75*p[3, 1] + 0.75*p[3, 2] - 0.25*p[3, 3]
            
            a[3, 0] = -0.5*p[0, 1] + 1.5*p[1, 1] - 1.5*p[2, 1] + 0.5*p[3, 1]
            a[3, 1] = 0.25*p[0, 0] - 0.25*p[0, 2] - 0.75*p[1, 0] + 0.75*p[1, 2] + 0.75*p[2, 0] - 0.75*p[2, 2] - 0.25*p[3, 0] + 0.25*p[3, 2]
            a[3, 2] = -0.5*p[0, 0] + 1.25*p[0, 1] - p[0, 2] + 0.25*p[0, 3] + 1.5*p[1, 0] - 3.75*p[1, 1] + 3*p[1, 2] - 0.75*p[1, 3] - 1.5*p[2, 0] + 3.75*p[2, 1] - 3*p[2, 2] + 0.75*p[2, 3] + 0.5*p[3, 0] - 1.25*p[3, 1] + p[3, 2] - 0.25*p[3, 3]
            a[3, 3] = 0.25*p[0, 0] - 0.75*p[0, 1] + 0.75*p[0, 2] - 0.25*p[0, 3] - 0.75*p[1, 0] + 2.25*p[1, 1] - 2.25*p[1, 2] + 0.75*p[1, 3] + 0.75*p[2, 0] - 2.25*p[2, 1] + 2.25*p[2, 2] - 0.75*p[2, 3] - 0.25*p[3, 0] + 0.75*p[3, 1] - 0.75*p[3, 2] + 0.25*p[3, 3]
            
            # 计算插值结果
            value = np.zeros(channel)
            for m in range(4):
                for n in range(4):
                    value += a[m, n] * (dx**n) * (dy**m)
            
            resized_image[i, j] = np.clip(value, 0, 255)
    
    return resized_image.astype(np.uint8)

# 双立方法插值实现图像旋转
def bicubic_rotation(image, angle):
    h, w, channel = image.shape
    angle_rad = math.radians(angle)
    
    # 计算旋转后的图像尺寸
    cos_theta = abs(math.cos(angle_rad))
    sin_theta = abs(math.sin(angle_rad))
    new_w = int(h * sin_theta + w * cos_theta)
    new_h = int(h * cos_theta + w * sin_theta)
    
    # 旋转中心
    cx, cy = w / 2, h / 2
    new_cx, new_cy = new_w / 2, new_h / 2
    
    rotated_image = np.zeros((new_h, new_w, channel))
    
    for i in range(new_h):
        for j in range(new_w):
            # 将新图像坐标转换回原图像坐标
            x = (j - new_cx) * math.cos(angle_rad) + (i - new_cy) * math.sin(angle_rad) + cx
            y = -(j - new_cx) * math.sin(angle_rad) + (i - new_cy) * math.cos(angle_rad) + cy
            
            if 0 <= x < w and 0 <= y < h:
                # 确定16个邻域像素的坐标
                x0 = max(0, int(np.floor(x)) - 1)
                x1 = x0 + 1
                x2 = x0 + 2
                x3 = min(w-1, x0 + 3)
                
                y0 = max(0, int(np.floor(y)) - 1)
                y1 = y0 + 1
                y2 = y0 + 2
                y3 = min(h-1, y0 + 3)
                
                # 获取16个邻域像素的值
                p = np.zeros((4, 4, channel))
                for m in range(4):
                    for n in range(4):
                        xi = x0 + n
                        yi = y0 + m
                        xi = min(max(xi, 0), w-1)  # 边界处理
                        yi = min(max(yi, 0), h-1)
                        p[m, n] = image[yi, xi]
                
                # 计算相对位置
                dx = x - x1
                dy = y - y1

                # 系数
                a = np.zeros((4, 4, channel))
                a[0, 0] = p[1, 1]
                a[0, 1] = -0.5*p[1, 0] + 0.5*p[1, 2]
                a[0, 2] = p[1, 0] - 2.5*p[1, 1] + 2*p[1, 2] - 0.5*p[1, 3]
                a[0, 3] = -0.5*p[1, 0] + 1.5*p[1, 1] - 1.5*p[1, 2] + 0.5*p[1, 3]
                
                a[1, 0] = -0.5*p[0, 1] + 0.5*p[2, 1]
                a[1, 1] = 0.25*p[0, 0] - 0.25*p[0, 2] - 0.25*p[2, 0] + 0.25*p[2, 2]
                a[1, 2] = -0.5*p[0, 0] + 1.25*p[0, 1] - p[0, 2] + 0.25*p[0, 3] + 0.5*p[2, 0] - 1.25*p[2, 1] + p[2, 2] - 0.25*p[2, 3]
                a[1, 3] = 0.25*p[0, 0] - 0.75*p[0, 1] + 0.75*p[0, 2] - 0.25*p[0, 3] - 0.25*p[2, 0] + 0.75*p[2, 1] - 0.75*p[2, 2] + 0.25*p[2, 3]
                
                a[2, 0] = p[0, 1] - 2.5*p[1, 1] + 2*p[2, 1] - 0.5*p[3, 1]
                a[2, 1] = -0.5*p[0, 0] + 0.5*p[0, 2] + 1.25*p[1, 0] - 1.25*p[1, 2] - p[2, 0] + p[2, 2] + 0.25*p[3, 0] - 0.25*p[3, 2]
                a[2, 2] = p[0, 0] - 2.5*p[0, 1] + 2*p[0, 2] - 0.5*p[0, 3] - 2.5*p[1, 0] + 6.25*p[1, 1] - 5*p[1, 2] + 1.25*p[1, 3] + 2*p[2, 0] - 5*p[2, 1] + 4*p[2, 2] - p[2, 3] - 0.5*p[3, 0] + 1.25*p[3, 1] - p[3, 2] + 0.25*p[3, 3]
                a[2, 3] = -0.5*p[0, 0] + 1.5*p[0, 1] - 1.5*p[0, 2] + 0.5*p[0, 3] + 1.25*p[1, 0] - 3.75*p[1, 1] + 3.75*p[1, 2] - 1.25*p[1, 3] - p[2, 0] + 3*p[2, 1] - 3*p[2, 2] + p[2, 3] + 0.25*p[3, 0] - 0.75*p[3, 1] + 0.75*p[3, 2] - 0.25*p[3, 3]
                
                a[3, 0] = -0.5*p[0, 1] + 1.5*p[1, 1] - 1.5*p[2, 1] + 0.5*p[3, 1]
                a[3, 1] = 0.25*p[0, 0] - 0.25*p[0, 2] - 0.75*p[1, 0] + 0.75*p[1, 2] + 0.75*p[2, 0] - 0.75*p[2, 2] - 0.25*p[3, 0] + 0.25*p[3, 2]
                a[3, 2] = -0.5*p[0, 0] + 1.25*p[0, 1] - p[0, 2] + 0.25*p[0, 3] + 1.5*p[1, 0] - 3.75*p[1, 1] + 3*p[1, 2] - 0.75*p[1, 3] - 1.5*p[2, 0] + 3.75*p[2, 1] - 3*p[2, 2] + 0.75*p[2, 3] + 0.5*p[3, 0] - 1.25*p[3, 1] + p[3, 2] - 0.25*p[3, 3]
                a[3, 3] = 0.25*p[0, 0] - 0.75*p[0, 1] + 0.75*p[0, 2] - 0.25*p[0, 3] - 0.75*p[1, 0] + 2.25*p[1, 1] - 2.25*p[1, 2] + 0.75*p[1, 3] + 0.75*p[2, 0] - 2.25*p[2, 1] + 2.25*p[2, 2] - 0.75*p[2, 3] - 0.25*p[3, 0] + 0.75*p[3, 1] - 0.75*p[3, 2] + 0.25*p[3, 3]
                
                # 计算插值结果
                value = np.zeros(channel)
                for m in range(4):
                    for n in range(4):
                        value += a[m, n] * (dx**n) * (dy**m)
                
                rotated_image[i, j] = np.clip(value, 0, 255)
    
    return rotated_image.astype(np.uint8)

图像插值算法优化：基于四平面

在上述的多种基于分段插值的图像插值算法中，均采用f(i, j)来表示图像的像素点坐标处的颜色值，其中ｉ表示行坐标，ｊ表示列坐标。为进一步地体现图像的局部特征差异并将其用于插值过程，我们引入“平面”的概念，并对图像数据进行升维处理，用三维空间点(i, j, f(i, j))来表示一个像素，并将其对应至空间坐标系中的一个点(x, y, z)。

对一个待插入点而言，可以通过坐标平移将其周围4 个像素点转换为：（注意：此处z0z3为像素坐标点s0s3的颜色值，下同）
$$
s_0(0,0,z_0),s_1(0,1,z_1),s_2(1,0,z_2),s_3(1,1,z_3)
$$
从上述４个点的坐标可以看出它们任意３个点一定不在同一条直线上， 不在同一直线上的３个点可以确定一个平面， 下面讨论具体的插值方法：

1. 先求出这４个点可能的４个平面方程

   已知空间平面的一般方程为：
   $$
   Ax+By+Cz+D=0
   $$
   将s0、s1、s2分别带入上式可得：
   $$
   \begin{cases}Cz_0+D=0\B+Cz_1+D=0\A+Cz_2+D=0&\end{cases}
   $$
   则有：
   $$
   D=-Cz_0,B=C(z_0-z_1),A=C(z_0-z_2)
   $$
   再将其带回空间平面方程，整理后用f(x, y)代替z得到插值公式：
   $$
   f(x,y)=(z_{2}-z_{0})x+(z_{1}-z_{2})y+z_{0}
   $$
   同理，将s0、s1、s3带入空间平面方程可得插值公式：
   $$
   f(x,y)=(z_{3}-z_{1})x+(z_{1}-z_{0})y+z_{0}
   $$
   将s0、s2、s3带入空间平面方程可得插值公式：
   $$
   f(x,y)=(z_{2}-z_{0})x+(z_{3}-z_{2})y+z_{0}
   $$
   将s1、s2、s3带入空间平面方程可得插值公式：
   $$
   f(x,y)=(z_{3}-z_{1})x+(z_{3}-z_{2})y+(z_{2}+z_{1}-z_{3})
   $$

2. 如果s0、s1、s2、s3这４ 个点在同一平面上， 则使用上述任意一个插值公式进行插值均可。 【平面法】

   判断这４个点是否在同一平面上， 只需要比较z1+z2 与 z0+z3是否相等：

   线段s0s3中点坐标为
   $$
   (\frac12,\frac12,\frac{z_0+z_3}2)
   $$
   线段s1s2中点坐标为
   $$
   (\frac12,\frac12,\frac{z_1+z_2}2)
   $$
   如果它们的中点坐标相同，则说明两条线段相交，相交的两条直线可以决定一个平面，即如果待插人点周围的四个点满足：
   $$
   z_1+z_2=z_0+z_3
   $$
   则这它们就是同一平面上的 4 个点，否则就不是同一平面上的 4 个点。

3. 从４个可能的平面中选择一个平面进行插值【四平面法】

   如果它们不是同一平面上的４个点， 情况比较复杂， 需认真讨论，s0、s1、s2、s3４个点的位置关系如下图所示：

   

   在插值的过程中如果一半的区域选择由s0、s1、s2 所确定的平面进行插值， 则另一半必须选择由s1、s2、s3所确定的平面进行插值， 以保证对角线的每一边都是在同一个平面上， 避免出现 “锯齿形” 边缘，为了便于描述， 称s0、s1、s2所确定的平面为 “左下平面”，s1、s2、s3 所确定的平面为 “右上平面”，s0、s1、s3 所确定的平面 “左上平面”，s0、s2、s3所确定的平面 “右下平面”。 为此， 需要参考周围其他点的情况以决定选择哪个平面进行插值。 具体情况如下图所示（黑点是待插入点周围的４个点，白点是参考点）：

   

   1. 对于“左下平面”， 只能参考s0、s1、s2三点左面和下面的点， 即s0、s1、s2三点与s4、s5、s6、s8四个点中的任意一点在同一平面上即可。
   2. 对于“右上平面”，只能参考s1、s2、s3三点右面和上面的点， 即s1、s2、s3三点与s7、s9、s10、s11四个点中的任意一点在同一平面上即可。
   3. 对于 “左上平面”，只能参考s0、s1、s3三点左面和上面的点， 即s0、s1、s3三点与s6、s8、s10、s11四个点中的任意一点在同一平面上即可。
   4. 对于 “右下平面”，只能参考s0、s2、s3三点右面和下面的点， 即s0、s2、s3三点与s4、s5、s7、s9四 个点中的任意一点在同一平面上即可。

   针对1、2两种情况， 当y = 1 + x时，用 “左下平面” 进行插值， 否则用 “右上平面” 进行插值；针对3、4两种情况， 当y = x ^ 3时，用 “左上平面” 进行插值， 否则用 “右下平面” 进行插值。

   判断４个点在同一平面上的方法：（以情况1为例）

   • 对于判断s0、s2、s1、s8 ４ 点是否在同一平面上， 只需要判断z0 + z1与z2 + z8是否相等即可；

   • 对于s0、s1、s2、s5 ４点， 只需要判断z0 + z2与z1 + z5是否相等即可；

   • 对于s0、s1、s2、s6 ４点：如果s0、s2、s6 ３点在同一直线上， 则直线外一点s1与该直线就可以确定一个平面，而要判断这三点是否在同一直线上，只需判断z2 + z6与2 * z0是否相等即可【线段s2(1, 0, z2) s6(-1, 0, z6) 的中点坐标为(0, 0, z2 + z6)，若z2 + z6 = 2 * z0， 则点s0(0, 0, z0)就是它们的中点坐标，当然这３点就在同一条直线上】；

   • 对于s0、s1、s2、s4 ４点， 与s0、s1、s2、s6 ４ 点的情况相同。

4. 如果2和3两点中的情形均不满足， 说明待插入点周围的情况太复杂（不符合平面插值）， 此时采用双线性法进行插值。

基于以上算法思想，编写python函数代码实现图像放缩与旋转过程中的四平面法插值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104

# 四平面法插值实现图像放缩
def four_plane_interpolation(img, scale):
    H, W, C = img.shape
    new_H, new_W = int(H * scale), int(W * scale)
    output = np.zeros((new_H, new_W, C), dtype=img.dtype)
    
    for y in range(new_H):
        for x in range(new_W):
            # 计算原图对应坐标（浮点数）
            src_x = x / scale
            src_y = y / scale
            
            # 获取周围4个整数坐标点
            x0, y0 = int(np.floor(src_x)), int(np.floor(src_y))
            x1, y1 = min(x0 + 1, W - 1), min(y0 + 1, H - 1)
            
            # 获取4个点的颜色值（z坐标）
            s0 = img[y0, x0]
            s1 = img[y0, x1]
            s2 = img[y1, x0]
            s3 = img[y1, x1]
            
            # 计算相对位置（归一化到[0,1]）
            dx = src_x - x0
            dy = src_y - y0
            
            # 判断四点是否共面（z1 + z2 ≈ z0 + z3）
            if np.allclose(s1 + s2, s0 + s3, atol=1e-6):
                # 共面时，选择任意平面（此处用左下平面）
                interpolated = s0 + (s2 - s0) * dx + (s1 - s0) * dy
            else:
                # 不共面时，动态选择平面
                # 获取周围12个参考点（简化实现，仅取最近邻）
                # 注：论文中需判断参考点是否共面，此处简化逻辑
                if dy > 1 - dx:  # 对角线 y = 1 - x 上方
                    # 选择右上平面
                    interpolated = (s3 - s1) * dx + (s3 - s2) * dy + (s2 + s1 - s3)
                else:
                    # 选择左下平面
                    interpolated = s0 + (s2 - s0) * dx + (s1 - s0) * dy
            
            # 边界检查
            interpolated = np.clip(interpolated, 0, 255 if img.dtype == np.uint8 else 1.0)
            output[y, x] = interpolated
    
    return output

# 四平面法插值实现图像旋转
def four_plane_rotation(image, angle):
    h, w, channel = image.shape
    angle_rad = math.radians(angle)
    
    # 计算旋转后的图像尺寸
    cos_theta = abs(math.cos(angle_rad))
    sin_theta = abs(math.sin(angle_rad))
    new_w = int(h * sin_theta + w * cos_theta)
    new_h = int(h * cos_theta + w * sin_theta)
    
    # 旋转中心
    cx, cy = w / 2, h / 2
    new_cx, new_cy = new_w / 2, new_h / 2
    
    rotated_image = np.zeros((new_h, new_w, channel), dtype=image.dtype)
    
    for i in range(new_h):
        for j in range(new_w):
            # 将新图像坐标转换回原图像坐标
            x = (j - new_cx) * math.cos(angle_rad) + (i - new_cy) * math.sin(angle_rad) + cx
            y = -(j - new_cx) * math.sin(angle_rad) + (i - new_cy) * math.cos(angle_rad) + cy
            
            # 边界检查
            if 0 <= x < w and 0 <= y < h:
                # 获取周围4个整数坐标点
                x0, y0 = int(np.floor(x)), int(np.floor(y))
                x1, y1 = min(x0 + 1, w - 1), min(y0 + 1, h - 1)
                
                # 获取4个点的颜色值
                s0 = image[y0, x0]
                s1 = image[y0, x1]
                s2 = image[y1, x0]
                s3 = image[y1, x1]
                
                # 计算相对位置
                dx = x - x0
                dy = y - y0
                
                # 判断四点是否共面
                if np.allclose(s1 + s2, s0 + s3, atol=1e-6):
                    # 共面时，选择任意平面（此处用左下平面）
                    interpolated = s0 + (s2 - s0) * dy + (s1 - s0) * dx
                else:
                    # 不共面时，动态选择平面
                    if dy > 1 - dx:  # 对角线 y = 1 - x 上方
                        # 选择右上平面
                        interpolated = (s3 - s1) * dx + (s3 - s2) * dy + (s2 + s1 - s3)
                    else:
                        # 选择左下平面
                        interpolated = s0 + (s2 - s0) * dy + (s1 - s0) * dx
                
                # 边界检查
                interpolated = np.clip(interpolated, 0, 255 if image.dtype == np.uint8 else 1.0)
                rotated_image[i, j] = interpolated
    
    return rotated_image

实验测试结果分析

一个理想的插值算法对一幅图像逆时针旋转若干度，再顺时针旋转若干度，应该与原图像相同；同理，对一幅图像放大若干倍，再缩小若干倍，也应该与原图像相同。 基于此，将下面的4幅图像分别用4种算法先逆时针旋转45°，再顺时针旋转45°；先放大４倍，再缩小４倍，然后分别用峰值信噪比（PSNR）验证各算法的优劣。

从定性实验的效果角度，上述四幅图像通过常用的三种分段插值算法完成上述的放大与旋转任务后得到的结果如下图所示：

从实验结果上来看，最近邻算法的边缘颜色“最醒目”，且出现了较为严重的“锯齿形”边缘现象；双线性算法的边缘颜色“最暗淡”；双线性算法和双三次算法也有“锯齿形”边缘现象， 但视觉效果相比最近邻算法而言并不明显。

通过改进的四平面插值算法，对上述四幅图像完成上述的放大与旋转任务后得到的结果如下图所示：

可以看到，四平面插值算法处理后的图像斜线边缘部分是 “光滑连续” 的， 视觉效果比较好，同时有效避免了“锯齿形”边缘现象和“马赛克”现象。

从定量实验的数据角度，我们对于各图像用不同算法完成上述旋转与放缩任务后得到的图像峰值信噪比与算法运行时间进行了计算与统计，结果如下表所示：

峰值信噪比(PSNR)用于表示信号的最大可能功率与影响其表示的保真度的破坏噪声的功率之间的比率。PSNR在图像处理上主要用于量化受有损压缩影响的图像和视频的重建质量。

PSNR 通过均方误差( MSE ) 定义。

给定一个无噪声的m×n单色图像I及其噪声近似值K，MSE定义为：
$$
MSE=\frac{1}{mn}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}[I(i,j)-K(i,j)]^2.
$$
故PSNR定义为：
$$
\begin{aligned}\mathrm{PSNR}&=10\cdot\log_{10}\left(\frac{MAX_I^2}{MSE}\right)\&=20\cdot\log_{10}\left(\frac{MAX_I}{\sqrt{MSE}}\right)\&=20\cdot\log_{10}(MAX_I)-10\cdot\log_{10}(MSE).\end{aligned}
$$
一般而言，通过PSNR来判断处理后图像的失真情况有如下通用结论：

• PSNR > 30 dB：图像质量较好，失真不明显。
• PSNR 20~30 dB：中等质量，存在可察觉失真。
• PSNR < 20 dB：质量较差，失真显著。

实际计算时，采用opencv自带的PSNR方法cv2.PSNR(img, output)对原始图像与处理后图像的PSNR进行比较计算。

通过对比上述定量实验结果可以发现，在传统的三种分段插值算法中，随着运算阶数（采样待插值点周围的原图像像素点颜色值信息）的增加，图像经过放缩与旋转处理后的失真程度有明显降低，但仍大致处于存在可察觉失真的区间，且算法运行用时也逐渐增加（事实上双立方法的实现可以在编程层面实现优化，这里只是为更直观地展现O（n^2）时间复杂度在图像大小达到一定规模时的显著影响）；而引入的四平面算法不仅在失真程度上较传统的插值算法均有显著改善，算法运行用时也明显优于传统算法中效果最好的双立方法。

综合以上的定性与定量实验结果及分析，本文提出的基于四平面的图像插值算法在图像处理效果（失真）与运行效率上均较传统算法有明显提升，这充分证明了该算法的有效性。

将上文提到的全部四种算法及旋转与放缩两种功能集成到基于python的gui可视化系统中，并打包成exe可执行文件，制作了一个基于插值的图像处理系统，基本功能演示如下图所示：

参考文献

[1] 王开荣,杨大地编著.应用数值分析[M].高等教育出版社,2010.

[2] 毛伟伟,于素萍,石念峰.一种基于四平面的图像插值算法[J].洛阳理工学院学报(自然科学版),2024,34(01):76-81.

[3] 刘显德,李笑.任意大小图像的量子描述及双线性插值方法[J].计算机工程与设计,2024,45(08):2423-2432.

[4] 张喜民,詹海生.基于双三次插值的Canny-Devernay亚像素图像边缘检测算法[J].现代制造工程,2025,(03):107-114.

[5] 陈玲玲,周宁,殷永,等.插值方法在光声图像重建中的应用[J].计算机与数字工程,2013,41(10):1676-1677+1694.

研究背景意义

矩阵的特征值计算虽然有比较可靠的理论方法，但是，理论方法只适合于矩阵规模很小或者只是在理论证明中起作用，而实际问题的数据规模都比较大，不太可能采用常规的理论解法。计算机擅长处理大量的数值计算，所以通过适当的数值计算理论，写成程序，让计算机处理，是一种处理大规模矩阵的方法，而且是一种好的方法。乘幂法（又称幂法）是求矩阵按模最大特征值的常用方法，其结构简单、便于使用，在实际工程中应用广泛：

• 在数值分析和优化问题中，乘幂法可通过求解矩阵按模最大特征值来得到其谱半径，从而帮助分析迭代算法的收敛性；
• 在物理学和工程学中，特征值问题常用于分析系统的稳定性、振动频率和模态分析，乘幂法能够有效求解系统的最大特征值，从而帮助理解系统的动态行为；
• 在图像处理中，特征值分解用于图像压缩、特征提取和模式识别，乘幂法可用于求解图像矩阵的最大特征值，从而实现高效的图像处理算法；
• ……

但该方法也存在一定的局限性，其只适用于求矩阵按模最大的特征值，而在实际问题中往往需要求矩阵全部特征值，如在主成分分析中需要求相关矩阵的全部特征值以确定各主成分的贡献率，在求解线性微分方程组中通过求系数矩阵的全部特征值以确定其基础解系；同时该方法在求特定矩阵（如具有一对互为相反数的按模最大特征值的矩阵等）的按模最大特征值时是不收敛的。因此，我们希望以乘幂法基本思想为出发点，在此基础上提出一些改进算法以对其进行泛化，使其能够解决更为广泛且通用的应用场景下的实际问题。

算法基本思想

设n阶矩阵A具有n个线性无关的特征向量
$$
x_1,x_2,…,x_n
$$
相应的特征值
$$
\lambda_1,\lambda_2,…,\lambda_n
$$
满足：
$$
\left|\lambda_1\right|>\left|\lambda_2\right|\geq\left|\lambda_3\right|\geq…\geq\left|\lambda_n\right|
$$
现任取一非零向量u_0，作迭代
$$
u_k=Au_{k-1}, k=0,1,2,…
$$
得到向量序列{u_k}(k=0,1,2,…)。因各特征向量线性无关，故n维向量u_0必可由他们线性表示，即：
$$
u_0=\alpha_{1}x_{1}+\alpha_{n}x_{2}+…+\alpha_{n}x_{n}
$$
显然有：
$$
\begin{aligned}u_{k}&=A^{k}v_{0}=\alpha_{1}A^{k}x_{1}+\alpha_{2}A^{k}x_{2}+\cdots+\alpha_{n}A^{k}x_{n}=\alpha_{1}\lambda_{1}^{k}x_{1}+\alpha_{2}\lambda_{2}^{k}x_{2}+\cdots+\alpha_{n}\lambda_{n}^{k}x_{n}\&=\lambda_{1}^{k}\left[\alpha_{1}x_{1}+\alpha_{2}\left(\frac{\lambda_{2}}{\lambda_{1}}\right)^{k}x_{2}+\cdots+\alpha_{n}\left(\frac{\lambda_{n}}{\lambda_{1}}\right)^{k}x_{n}\right]\end{aligned}
$$
设
$$
\alpha_{1} \neq 0
$$
由
$$
\left|\frac{\lambda_{i}}{\lambda_{1}}\right|<1,i=2,3,\cdots,n
$$
可得：
$$
\operatorname*{lim}{k\to\infty}\frac{u{k}}{\lambda_{1}^{k}}=\operatorname*{lim}{k\to\infty}\frac{\lambda{1}^{k}\left[\alpha_{1}x_{1}+\sum_{i=2}^{n}\alpha_{i}\left(\frac{\lambda_{i}}{\lambda_{1}}\right)^{k}x_{i}\right]}{\lambda_{1}^{k}}=\operatorname*{lim}{k\to\infty}\left[\alpha{1}x_{1}+\sum_{i=2}^{n}\alpha_{i}\left(\frac{\lambda_{i}}{\lambda_{1}}\right)^{k}x_{i}\right]=\alpha_{1}x_{1}
$$

$$
\operatorname*{lim}{k\to\infty}\frac{\left(u{k+1}\right){m}}{\left(u{k}\right){m}}=\operatorname*{lim}{k\to\infty}\frac{\left{\lambda_{1}^{k+1}\left[\alpha_{1}x_{1}+\sum_{i=2}^{n}\alpha_{i}\left(\frac{\lambda_{i}}{\lambda_{1}}\right)^{k+1}x_{i}\right]\right}{m}}{\left{\lambda{1}^{k}\left[\alpha_{1}x_{1}+\sum_{i=2}^{n}\alpha_{i}\left(\frac{\lambda_{i}}{\lambda_{i}}\right)^{k}x_{i}\right]\right}{m}}=\lambda{1}\frac{\left(x_{1}\right){m}}{\left(x{1}\right){m}}=\lambda{1}
$$

这表明向量序列u_k具有收敛性，其收敛速度由比值
$$
\left|\frac{\lambda_{2}}{\lambda_{1}}\right|
$$
确定，该比值越小说明收敛速度越快，比值越接近于1收敛速度就越慢。

同时，该结论表明，当k取得足够大时（在实际应用时往往认为某次迭代前后误差小于设定的误差限即满足该条件），有：
$$
u_{k}≈\lambda_{1}^{k}\alpha_{1}x_{1}, \lambda_{1}≈\frac{\left(u_{k+1}\right)}{\left(u_{k}\right)}
$$
即u_ k可近似看作特征值λ_ 1对应的特征向量（较原特征向量x_ 1而言仅乘上了有限的常数系数，其结果仍为该特征值对应的特征向量），而对应的按模最大特征值λ_ 1的估计值可由前后两次迭代的特征向量u_ k相除得到。

当矩阵的按模最大特征值是重根时，上述结论仍然成立。设λ_ 1为r重根，即：
$$
\lambda_{1}=\lambda_{2}=\cdots=\lambda_{r}
$$
且满足条件
$$
\mid\lambda_{r}\mid>\mid\lambda_{r+1}\mid\geq\cdots\geq\mid\lambda_{n}\mid
$$
则有：
$$
u_{k}=A^{k}u_{0}=\lambda_{1}^{k}\left[\sum_{i=1}^{r}\alpha_{i}x_{i}+\sum_{j=r+1}^{n}\alpha_{j}\left(\frac{\lambda_{j}}{\lambda_{1}}\right)^{k}x_{j}\right]
$$
易推得（式中(u_ k)_ m表示向量u_ k的第m个分量）：
$$
\lim_{k\to\infty}\frac{u_{k}}{\lambda_{i}^{k}}=\sum_{i=1}^{^{r}}\alpha_{i}x_{i},\lim_{k\to\infty}\frac{\left(u_{k+1}\right){m}}{\left(u{k}\right){m}}=\lambda{1}
$$
与一般情况略有不同的是，此时
$$
u_{k}≈\lambda_{i}^{k}\sum_{i=1}^{^{r}}\alpha_{i}x_{i}
$$
但事实上我们并没有办法在求解之前事先预知一个矩阵是否具有r重按模最大特征值，因此在实际操作的过程中采用与一般情形相同的处理方式（即认为r=1），所得的向量序列u_k仍然收敛，不影响求解结果。

基于以上的算法原理，可以编写如下MATLAB程序，实现一般情况下矩阵按模最大特征值及其对应特征向量的计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

function calculatePowerMethod(matrixEdit, iterEdit)
    % 获取用户输入的矩阵matrixEdit和最大迭代次数iterEdit
    A = str2num(matrixEdit.Value); % 将字符串转换为矩阵
    n = length(A);
    V = rand(n,1);  % 以随机方式初始化迭代向量u0
    max_iter = iterEdit.Value;    % 获取迭代次数

    Eps = 1E-4; % 迭代精度
    k = 0; % 初始迭代次数
    lambda0 = 0;

    % 乘幂法迭代，求得矩阵按模最大特征值lambda及其对应特征向量v
    while k <= max_iter - 1
        v = A * V;
        [vmax, i] = max(abs(v));
        lambda = v(i) / V(i);
        V = v;
        if abs(lambda - lambda0)<Eps
            k = k + 1;
            break;
        end
        lambda0 = lambda;
        k = k + 1;
    end
end

改进的乘幂法

在实际应用层面，上述的算法逻辑只在一小部分的常规矩阵上对于矩阵的按模最大特征值求解有较好效果。事实上，仅依托以上的代码逻辑进行求解往往会出现以下几大问题：

1. 当矩阵A不具有n个线性无关的特征向量时（事先无法判断），乘幂法不适用。
2. 当待求取的按模最大特征值abs(λ_ 1)>1时，迭代向量u_ k的各个分量可能会随着abs(λ_ 1)^k变得很大而使计算机“上溢”；而当待求取的按模最大特征值abs(λ_ 1)<1时，迭代向量u_ k的各个分量可能会随着abs(λ_ 1)^k变得很小使u_k成为零向量。
3. 矩阵的按模最大特征值是一对相反数。
4. 矩阵的按模最大特征值是一对共轭复数。

（上述算法中还给出了α_1≠0的假设，事实上如果不满足这一点也不影响乘幂法的成功使用。因为舍入误差的影响，在迭代某一步会产生u_k在x_1方向上的分量不为零，以后的迭代仍会收敛）

针对问题1，我们暂时无法提出具有针对性的解决方案，但后续的实际测试证明，当迭代次数k足够大时，我们针对问题3所提出的改进方案在该种情况下相比基本算法能够有更好的收敛性（收敛更快）；针对问题2，我们可以通过将向量序列u_k进行规范化处理，限制向量的模在特定小范围内，防止计算机运算的上下溢出；针对问题3，我们在原有的乘幂法算法思想的基础上进行了改进，改进后的算法能够有效对原算法无法求解（不收敛）的按模最大特征值互为相反数的矩阵的按模最大特征值进行有效求解；针对问题4，我们目前还没有找到有效的解决方案。

迭代向量的归一化

设迭代向量u为非零向量，将其归一化得到向量
$$
y=\frac{u}{max(u)}
$$
其中max(u)表示向量u的模最大的分量（即向量的无穷范数）。这样的规范化会保证每一次迭代后得到的新的迭代向量的模最大分量均为1，这有效起到了限制迭代向量分量范围的作用，能够很好地解决上述提到的问题2。值得注意的是，对向量规范化的方式并不只有归一化这一种，实际上可以使用任意一种范数对向量进行规范化处理，如2范数等。可以证明，对于基于不同范数的归一化都有相同的向量序列收敛结论，下面以无穷范数为例给出基本的证明。（显然这样的规范化只是在原有的向量基础上除以了某一个常数，这并不会改变向量序列的收敛性）

取初始向量
$$
u_{0}\neq0
$$
规范化得
$$
y_{0}=\frac{u_{0}}{\max(u_{0})}
$$
构造向量序列：
$$
\begin{aligned}
&u_{1}=Ay_{0}=\frac{Au_{0}}{\max(u_{0})},
&y_{1}=\frac{u_{1}}{\max(u_{1})}=\frac{Au_{0}}{\max(Au_{0})}\
&u_{2}=Ay_{1}=\frac{A^{2}u_{0}}{\max(Au_{0})},
&y_{2}=\frac{u_{2}}{\max(u_{2})}=\frac{A^{2}u_{0}}{\max(A^{2}u_{0})}\
&……\
&u_{k}=Ay{{k-1}}=\frac{A^{k}u{0}}{\max(A^{k-1}u_{0})},
&\quad y_{k}=\frac{u_{k}}{\max(u_{k})}=\frac{A^{k}u_{0}}{\max(A^{k}u_{0})}
\end{aligned}
$$
结合乘幂法基本算法中已经证明的结论
$$
A^{k}u_{0}=u_{k}≈\lambda_{1}^{k}\alpha_{1}x_{1}
$$
则有：
$$
\lim_{k\to\infty}y_{k}=\frac{x_{1}}{\max(x_{1})},
\lim_{k\to\infty}\max(u_{k})=\lambda_{1}
$$
这表明此时y_ k可近似看作特征值λ_ 1对应的特征向量（较原特征向量x_ 1而言仅进行了归一化处理，其结果仍为该特征值对应的特征向量），而对应的按模最大特征值λ_ 1的估计值可近似看作未归一化前的迭代向量最大分量值max(u_k)。

基于以上的算法原理，可以编写如下MATLAB程序，实现归一化处理下矩阵按模最大特征值及其对应特征向量的计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

function calculatePowerMethod(matrixEdit, iterEdit)
    % 获取用户输入的矩阵matrixEdit和最大迭代次数iterEdit
    A = str2num(matrixEdit.Value); % 将字符串转换为矩阵
    n = length(A);
    V = rand(n,1);  % 以随机方式初始化迭代向量u0
    max_iter = iterEdit.Value;    % 获取迭代次数

    Eps = 1E-4; % 迭代精度
    k = 0; % 初始迭代次数
    lambda0 = 0;

    % 乘幂法迭代，求得矩阵按模最大特征值lambda及其对应特征向量v
    while k <= max_iter - 1
        v = A * V;
        [vmax, i] = max(abs(v));
        lambda = v(i);
        V = v / lambda;
        if abs(lambda - lambda0)<Eps
            k = k + 1;
            break;
        end
        lambda0 = lambda;
        k = k + 1;
    end
end

归一化乘幂法的进一步改进

针对问题3，从其基本情形出发（其他条件与先前保持一致），即有：
$$
\mid\lambda_1\mid=\mid\lambda_2\mid>\mid\lambda_3\mid\geqslant\cdotp\cdotp\cdotp\geqslant\mid\lambda_n\mid，\lambda_1=-\lambda_2
$$
在矩阵按模最大特征值为一对相反数的情况下，原迭代向量序列中各相邻向量的比值极限发散：
$$
\lim_{k\to\infty}\frac{\boldsymbol{u}_{k+1}}{\boldsymbol{u}k}=\lambda_1\lim{k\to\infty}\frac{a_1\boldsymbol{x}_1+(-1)^{k+1}a_2\boldsymbol{x}2+\boldsymbol{\varepsilon}{k+2}}{a_1\boldsymbol{x}_1+(-1)^ka_2\boldsymbol{x}_2+\boldsymbol{\varepsilon}_k}
$$
说明在该种情况下，采用原有的乘幂法基本算法，得到的迭代向量序列并不收敛，无法得到稳定的矩阵按模最大特征值数值求解结果。

我们在原有算法的基础上进行了一定的改进，构造了新的迭代向量序列，使其对于矩阵按模最大特征值为一对相反数的情况也能保证收敛，从而可以对该情况下的矩阵按模最大特征值进行有效求解。

先从较为简单的非归一化迭代入手，同样取迭代向量序列u_k，其初始非零向量u_0满足：
$$
u_0=\alpha_{1}x_{1}+\alpha_{n}x_{2}+…+\alpha_{n}x_{n}(\alpha_{1}\neq0)
$$
则有：
$$
\boldsymbol{u}{k}=\boldsymbol{A}^{k}\left(\sum{i=1}^{n}a_{i}\boldsymbol{x}{i}\right)=\lambda{1}^{k}\left(a_{1}\boldsymbol{x}{1}+(-1)^{k}a{2}\boldsymbol{x}{2}+\sum{i=3}^{n}\left(\frac{\lambda_{i}}{\lambda_{1}}\right)^{k}a_{i}\boldsymbol{x}{i}\right)=\lambda{1}^{k}(a_{1}\boldsymbol{x}{1}+(-1)^{k}a{2}\boldsymbol{x}{2}+\boldsymbol{\varepsilon}{k}),\lim_{k\to\infty}\varepsilon_{k}=0
$$
于是可得到：
$$
\lim_{k\to\infty}\frac{u_{k+2}}{u_{k}}=\lambda_{1}^{2}\lim_{k\to\infty}\frac{\alpha_{1}x_{1}+(-1)^{k+2}\alpha_{2}x_{2}+\varepsilon_{k+2}}{\alpha_{1}x_{1}+(-1)^{k}\alpha_{2}x_{2}+\varepsilon_{k}}=\lambda_{1}^{2}
$$
且有：
$$
\lim_{k\to\infty}\frac{u_{k+1}+\lambda_1u_k}{\lambda_1^{k+1}}=2\alpha_1x_1
$$
以上结果说明，在矩阵按模最大特征值为一对相反数（正值λ_ 1，负值λ_ 2）的情形下，若采用原有的迭代向量序列，对序列中的向量一隔一取出，构成的新序列是收敛的，且新序列中的相邻两项向量的比值极限为矩阵按模最大特征值的平方；同时，u_ {k+1}+λ_ {1}u_ {k}可近似看作λ_ {1}的特征向量，同理u_ {k+1}+λ_ {2}u_ {k}也可近似看作λ_ {2}的特征向量。

易证该方法对于规范化后的向量序列也具有相同的收敛性，在此不额外给出证明。

在实际编程实现算法时，为尽可能地节省算力与内存并提高计算效率，我们不会预先求取最大迭代次数内每一次迭代的结果再将其分为两个向量序列判断其是否收敛（相邻向量插值小于设定误差限），而是需要结合上述改进算法与逐步迭代过程，对于每一次迭代的求解过程进行逻辑优化，优化后的逻辑如下所示（u_k代表规范化后的迭代向量序列，采用2范数方式进行规范化，k=1,2,…）：

• 若
  $$
  \left|\frac{\left(\boldsymbol{u}_{k+2}^{(1)}\right)_i}{\left(\boldsymbol{u}_k^{(1)}\right)i}-\frac{\left(\boldsymbol{u}{k+1}^{(1)}\right)i}{\left(\boldsymbol{u}{k-1}^{(1)}\right)_i}\right|<\varepsilon:,

  \left|\frac{\left(\boldsymbol{u}_{k+2}^{(1)}\right)i}{\left(\boldsymbol{u}{k+1}^{(1)}\right)i}-\frac{\left(\boldsymbol{u}{k+1}^{(1)}\right)_i}{\left(\boldsymbol{u}_k^{(1)}\right)i}\right|<\varepsilon:
  $$
  则取矩阵按模最大特征值
  $$
  \lambda_1=\frac{(\boldsymbol{u}{k+2}^{(1)})i}{(\boldsymbol{u}{k+1}^{(1)})i}
  $$
  对应的特征向量
  $$
  x_1=u{k+2}^{(1)}
  $$

• 若
  $$
  \left|\frac{\left(\boldsymbol{u}_{k+2}^{(1)}\right)_i}{\left(\boldsymbol{u}_k^{(1)}\right)i}-\frac{\left(\boldsymbol{u}{k+1}^{(1)}\right)i}{\left(\boldsymbol{u}{k-1}^{(1)}\right)_i}\right|<\varepsilon:,

  \left|\frac{(\boldsymbol{u}{k+2}^{(1)})i}{(\boldsymbol{u}{k+1}^{(1)})i}-\frac{(\boldsymbol{u}{k+1}^{(1)})i}{(\boldsymbol{u}k^{(1)})i}\right|>\varepsilon:
  $$
  则取矩阵按模最大特征值
  $$
  \lambda_1=\pm\sqrt{\frac{(\boldsymbol{u}{k+2}^{(1)})i}{(\boldsymbol{u}{k}^{(1)})i}}
  $$
  对应的特征向量
  $$
  x_1=\frac{u{k+2}^{(1)}+\lambda_1u{k+1}^{(1)}}{\parallel u{k+2}^{(1)}+\lambda_1u{k+1}^{(1)}\parallel_2}
  $$

基于以上的算法原理，可以编写如下MATLAB程序，实现矩阵按模最大特征值及其对应特征向量求解的改进算法，以解决矩阵按模最大特征值可能为一对相反数的特殊情况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

function calculatePowerMethod1(matrixEdit, iterEdit, fig)
    % 获取用户输入的矩阵matrixEdit和最大迭代次数iterEdit
    A = str2num(matrixEdit.Value); % 将字符串转换为矩阵
    n = length(A);
    V = rand(n,1);  % 以随机方式初始化迭代向量u0
    max_iter = iterEdit.Value;    % 获取迭代次数

    Eps = 1E-4; % 迭代精度
    k = 0; % 初始迭代次数

    % 乘幂法迭代，求得矩阵按模最大特征值lambda及其对应特征向量v
    while k <= max_iter - 1
        v = A * V;
        v1 = A * v;
        v_2 =norm(v, 2);
        minus1 = A * v1 ./ v - v1 ./ V;
        minus2 = A * v1 ./ v1 - v1 ./ v;
        if max(abs(minus1(:))) < Eps
            if max(abs(minus2(:))) < Eps
                lambda0 = A * v1 ./ v1;
                lambda = max(lambda0(:));
                v2_2 = norm(A * v1, 2);       
                v = A * v1 / v2_2;
            else
                lambda0 = A * v1 ./ v;
                lambda = sqrt(max(lambda0(:)));
                v3 = A * v1 + lambda * v1;
                v3_2 = norm(v3, 2);
                v = v3 / v3_2;
            end
            k = k + 1;
            break;
        end
        k = k + 1;
        V = v / v_2;
        lambda0 = A * v1 ./ v1;
        lambda = max(lambda0(:));
    end
end

求实对称矩阵的全部特征值

我们知道，实对称矩阵的不同特征值对应的特征向量一定是正交的，因此，可以通过幂法迭代得到矩阵的主特征值λ_ 1和主特征向量x_ 1 ，再重新给出一个新的与v_ 0线性无关的初始迭代向量v_ 1，使v_ 1和x_ 1正交化， 则可以由幂法迭代出矩阵的特征值λ_ 2和特征向量x_ 2。同样使新给出的初始迭代向量v_ 3和x_ 1、x_ 2正交 化，则可以由幂法得到λ_ 3和x_ 3。以此类推，可以计算出矩阵的全部特征值和特征向量。具体证明过程详见参考文献[3]，这里仅给出基于上述改进算法的完整算法逻辑：

令
$$
A_j=\mathbf{A}{j-1}-\lambda{j-1}\boldsymbol{x}{j-1}\boldsymbol{x}{j-1}^{\mathrm{T}}(j=2,3,\cdots n)
$$
采取与先前完全相同的迭代向量序列构造方式，有如下判断逻辑（u_k代表规范化后的迭代向量序列，采用2范数方式进行规范化，k=1,2,…）：

• 若
  $$
  \left|\frac{(u_{k+2}^{(j)})i}{(u_k^{(j)})i}-\frac{(u{k+1}^{(j)})i}{(u{k-1}^{(j)})i}\right|<\varepsilon:,\quad\left|\frac{(u{k+2}^{(j)})i}{(u{k+1}^{(j)})i}-\frac{(u{k+1}^{(j)})i}{(u_k^{(j)})i}\right|<\varepsilon:,
  $$
  且满足
  $$
  {|x{m}^{\mathrm{T}}v{k+2}^{(j)}|<\varepsilon}\left(m=1,2,\cdots,j-1\right)
  $$
  则取矩阵按模最大特征值
  $$
  {\lambda{j}}=\frac{\left(\boldsymbol{u}{k+2}^{(j)}\right){i}}{\left(\boldsymbol{u}{k+1}^{(j)}\right){i}}
  $$
  对应的特征向量
  $$
  x_{j}=\boldsymbol{u}_{k+2}^{(j)}
  $$

• 若
  $$
  \left|\frac{(u_{k+2}^{(j)})i}{(u_k^{(j)})i}-\frac{(u{k+1}^{(j)})i}{(u{k-1}^{(j)})i}\right|<\varepsilon:,\quad\left|\frac{(u_{k+2}^{(j)})_i}{(u_{k+1}^{(j)})_i}-\frac{(u_{k+1}^{(j)})_i}{(u_k^{(j)})_i}\right|>\varepsilon:,
  $$
  且满足
  $$
  \left|\boldsymbol{x}{m}^{\mathrm{T}}\frac{\boldsymbol{u}{k+2}^{(j)}+\lambda_{j}\boldsymbol{u}{k+1}^{(j)}}{\parallel\boldsymbol{u}{k+2}^{(j)}+\lambda_{j}\boldsymbol{u}{k+1}^{(j)}\parallel{2}}\right|<\varepsilon\quad(m=1,2,\cdots,j-1)
  $$
  则取矩阵按模最大特征值
  $$
  \lambda_{j}=\pm\sqrt{\frac{(\boldsymbol{u}{k+2}^{(j)}){i}}{(\boldsymbol{u}{k}^{(j)}){i}}}
  $$
  对应的特征向量
  $$
  \quad x_{j}=\frac{\boldsymbol{u}{k+2}^{(j)}+\lambda{j}\boldsymbol{u}{k+1}^{(j)}}{\parallel\boldsymbol{u}{k+2}^{(j)}+\lambda_{j}\boldsymbol{u}{k+1}^{(j)}\parallel{2}}
  $$

基于以上的算法原理，可以编写如下MATLAB程序，实现矩阵按模最大特征值及其对应特征向量求解的改进算法，并对于实对称矩阵的全部特征值进行依次求解（每次运行该函数进行一个特征值的求解，代码中省去了存储用于求解下一个特征值的矩阵作为全局变量的部分）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

function calculatePowerMethod2(iterEdit, fig)
    % 从存储的全局变量中读取需要求解主特征值的新矩阵data.matrix
    A = data.matrix; % 将字符串转换为矩阵
    n = length(A);
    V = rand(n,1); 
    max_iter = iterEdit.Value;    % 获取迭代次数

    Eps = 1E-4; % 迭代精度
    k = 0; % 初始迭代次数

    % 乘幂法迭代，求得矩阵按模最大特征值lambda及其对应特征向量v
    while k <= max_iter - 1
        v = A * V;
        v1 = A * v;
        v_2 =norm(v, 2);
        v2_2 = norm(A * v1, 2);
        v2 = A * v1 / v2_2;
        lambda0 = A * v1 ./ v;
        lambda = sqrt(max(lambda0(:)));
        v3 = A * v1 + lambda * v1;
        v3_2 = norm(v3, 2);
        minus1 = A * v1 ./ v - v1 ./ V;
        minus2 = A * v1 ./ v1 - v1 ./ v;
        if max(abs(minus1(:)))<Eps
            num1 = 0;
            num2 = 0;
            for l = 1 : j
                x = full_V(:,l);
                if max(abs(minus2(:))) < Eps && abs(x' * v2) < Eps
                    num1 = num1 + 1;
                elseif max(abs(minus2(:))) > Eps && abs(x' * v3 / v3_2) < Eps
                    num2 = num2 + 1;
                end
            end
            if num1 == j
                lambda0 = A * v1 ./ v1;
                lambda = max(lambda0(:));
                v = A * v1 / v2_2;
                k = k + 1;
                break;
            elseif num2 == j
                lambda0 = A * v1 ./ v;
                lambda = sqrt(max(lambda0(:)));
                v = v3 / v3_2;
                k = k + 1;
                break;
            end
        end
        k = k + 1;
        V = v / v_2;
        lambda0 = A * v1 ./ v1;
        lambda = max(lambda0(:));
    end
end

数据测试实验

针对以上提到的乘幂法及其改进算法，将其MATLAB求解代码整合进GUI中，并对求解过程中矩阵按模最大特征值随迭代次数增加的收敛情况进行可视化，基本界面如下：

乘幂法基础算法

将待求解的矩阵按照格式要求输入框体内，并指定最大迭代次数（默认为100次），按下“计算”控件可以利用基础的乘幂法（归一化版本）对矩阵按模最大特征值及其对应特征向量进行求解，同时会调用MATLAB中自带的矩阵特征值求解函数eig()对求解结果进行验证。

例：矩阵（特征值为-1、3、5）

$$
A=\begin{pmatrix}1&-1&2\-2&0&5\6&-3&6\end{pmatrix}
$$

程序求解与可视化结果：

可以发现，估计的主特征值与实际的主特征值在限定的精度内基本一致，对应的特征向量相差了相同的倍数，也可视为正确求解。

乘幂法改进算法

将待求解的矩阵按照格式要求输入框体内，并指定最大迭代次数（默认为100次），按下“优化计算”控件可以利用改进的乘幂法（归一化版本）对矩阵按模最大特征值及其对应特征向量进行求解，同时会调用MATLAB中自带的矩阵特征值求解函数eig()对求解结果进行验证。

例1：矩阵（特征值为-1、3、5）

$$
A=\begin{pmatrix}1&-1&2\-2&0&5\6&-3&6\end{pmatrix}
$$

程序求解与可视化结果：

可以发现，估计的主特征值与实际的主特征值在限定的精度内保持一致，通过该算法计算得到的对应特征向量也与MATLAB自带函数（基于 Cholesky 分解/QR分解方法的特征值求解）的求解结果在限定精度内完全一致，但计算需要的迭代次数较基础算法而言有明显增加。

例2：矩阵（特征值为3、-3、1，按模最大特征值为一对相反数）

$$
A=\begin{pmatrix}3&-2&4\0&-3&2\0&0&1\end{pmatrix}
$$

程序求解与可视化结果：

调用乘幂法基本算法：

调用乘幂法改进算法：

可以发现：

• 调用基础算法时，迭代向量序列在设定的最大迭代次数内并不收敛，最终的求解结果也与实际按模最大特征值有较大误差；
• 而调用改进算法时，尽管从主特征值收敛过程的可视化结果中无法确定向量序列的收敛性（实际上原序列仍发散），但序列中的向量一隔一选取构成的新序列（图像中对应迭代次数全为奇数/偶数的震荡单边）已由程序判断收敛，且估计的主特征值与实际的主特征值在限定的精度内保持一致，通过该算法计算得到的对应特征向量也与MATLAB自带函数（基于 Cholesky 分解/QR分解方法的特征值求解）的求解结果在限定精度内完全一致。

例3：3阶矩阵（特征值为3（重根），但不具有3个线性无关的特征向量）

$$
A=\begin{pmatrix}3&1&0\0&3&1\0&0&3\end{pmatrix}
$$

程序求解与可视化结果：

调用乘幂法基本算法（最大迭代次数100）：

调用乘幂法改进算法（最大迭代次数100）：

调用乘幂法基本算法（最大迭代次数10000）：

调用乘幂法改进算法（最大迭代次数10000）：

可以发现，当矩阵不具有n个线性无关的特征向量时，乘幂法从理论上讲不再适用（不满足假设条件），但实际测试可以发现：

• 当最大迭代次数设置较小（100）时，两种方法均未呈现数值上的收敛（两次迭代间误差不超过设定误差限10^(-4)），所求得的主特征值与对应特征向量与真实值之间均有明显误差；
• 当最大迭代次数设置足够大（10000）时，两种方法在迭代次数达到10^2数量级时实现了数值上的收敛（两次迭代间误差不超过设定误差限10^(-4)），但在停止迭代后，通过乘幂法基础算法求得的主特征值与对应特征向量与真实值之间仍有明显误差，而通过改进算法求得的主特征值与对应特征向量与真实值已经基本接近，但改进算法所需要的迭代次数也明显更多。

但总的来说，从理论角度出发，在这种情况下乘幂法已不再适用，本例的情况仅为收敛较慢，此时改进算法相较于基础算法有更好的精度；但也会有不收敛的情况，此时两种方法均会有比较大的误差，而这是无法事先判断的，因此在使用乘幂法时还是尽量避免该种情况，或者说在优化算法仍然无法快速收敛的情况下需要注意到矩阵不具有n个线性无关的特征向量的特殊情况，此时应选取其他合适的特征值求解算法。

例4：矩阵（特征值为1+2i、1-2i、0.5，按模最大特征值为一对共轭复数）

$$
A=\begin{pmatrix}1&-2&0\2&1&0\0&0&0.5\end{pmatrix}
$$

程序求解与可视化结果：

调用乘幂法基本算法：

调用乘幂法改进算法：

此情况下两种乘幂法均呈现了极大的不稳定性，无法正确求解。

求实对称矩阵的全部特征值

例1：矩阵（特征值为-1、3、5）

$$
A=\begin{pmatrix}1&-1&2\-2&0&5\6&-3&6\end{pmatrix}
$$

程序求解与可视化结果：

该矩阵不为对称矩阵，无法通过上述算法实现全部特征值的求解，为排错示例。

例2：对称矩阵（特征值为1、2、4）

$$
A=\begin{pmatrix}3&1&1\1&2&0\1&0&2\end{pmatrix}
$$

程序求解与可视化结果：

可以看到，该算法可以用于正确求取实对称矩阵的所有特征值及其相应的特征向量，求解结果与MATLAB自带函数（基于 Cholesky 分解/QR分解方法的特征值求解）的求解结果在限定精度内完全一致。

例3：对称矩阵（特征值为2、1、-1）

$$
A=\begin{pmatrix}1&1&0\1&0&1\0&1&1\end{pmatrix}
$$

程序求解与可视化结果：

可以看到，即使在矩阵的次主特征值为一对相反数的情况下，该算法也可以用于正确求取实对称矩阵的所有特征值及其相应的特征向量，求解结果与MATLAB自带函数（基于 Cholesky 分解/QR分解方法的特征值求解）的求解结果在限定精度内完全一致。

参考文献

[1] 王开荣,杨大地编著.应用数值分析[M].高等教育出版社,2010.

[2] 曹连英,曲智林,杨瑞智.基于幂法的求实对称矩阵特征值的注记[J].大学数学,2024,40(04):67-72.

[3] 曾莉,肖明.计算实对称矩阵特征值特征向量的幂法[J].南昌大学学报(理科版),2016,40(04):399-402.

[4] 张青,苟国楷,吕崇德.乘幂法的改进算法[J].应用数学与计算数学学报,1997,(01):51-55.

[5] 马志勇,方珑.矩阵特征值求解及其在图像压缩中的应用[J].上海第二工业大学学报,2012,29(04):315-318.