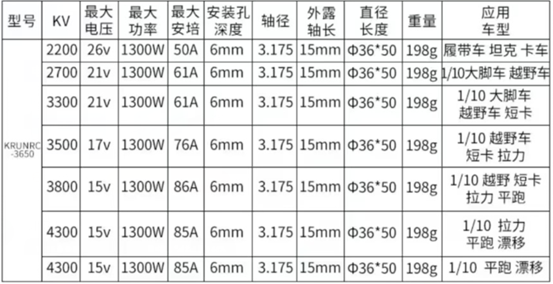
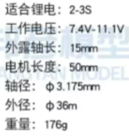
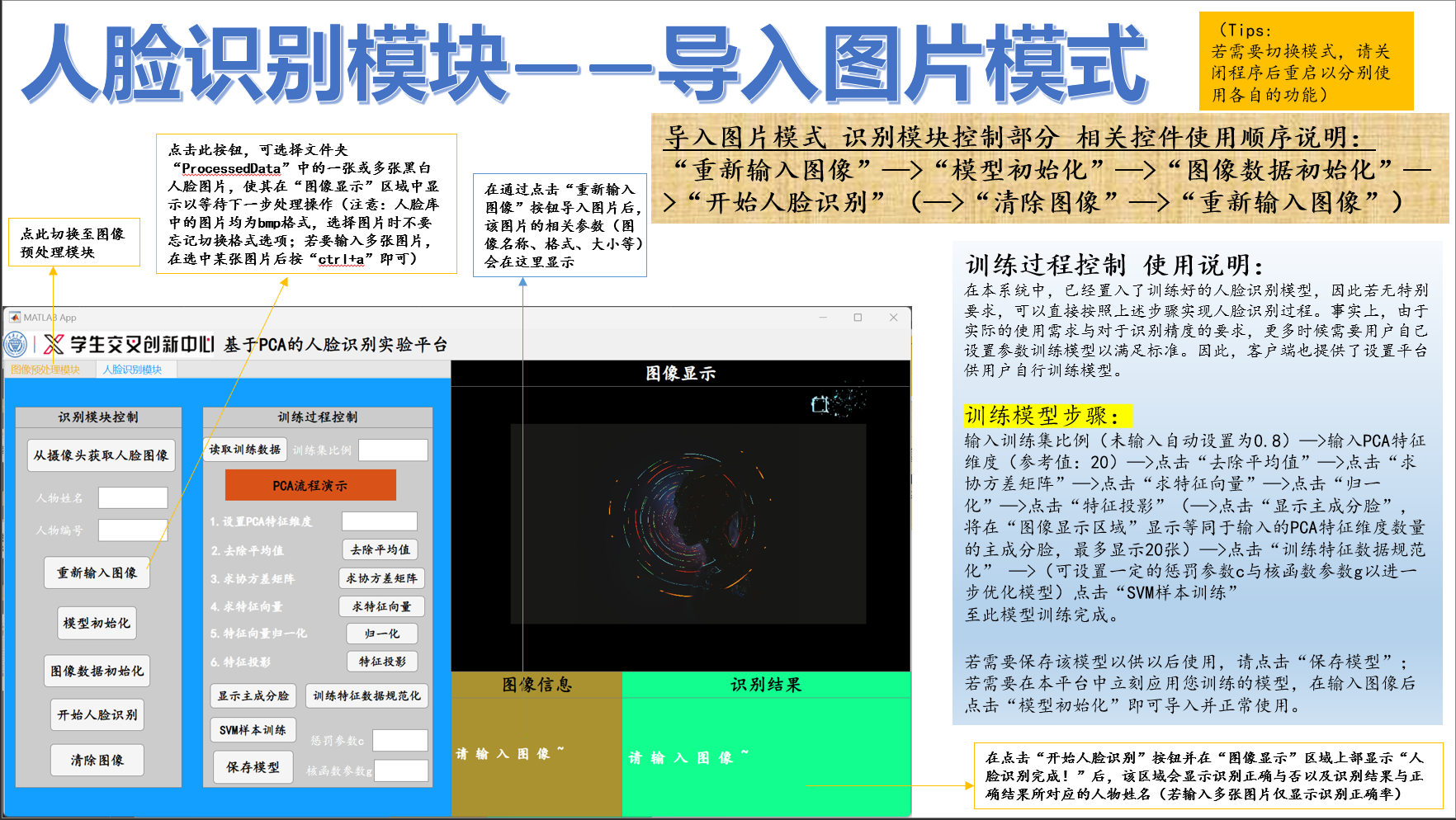
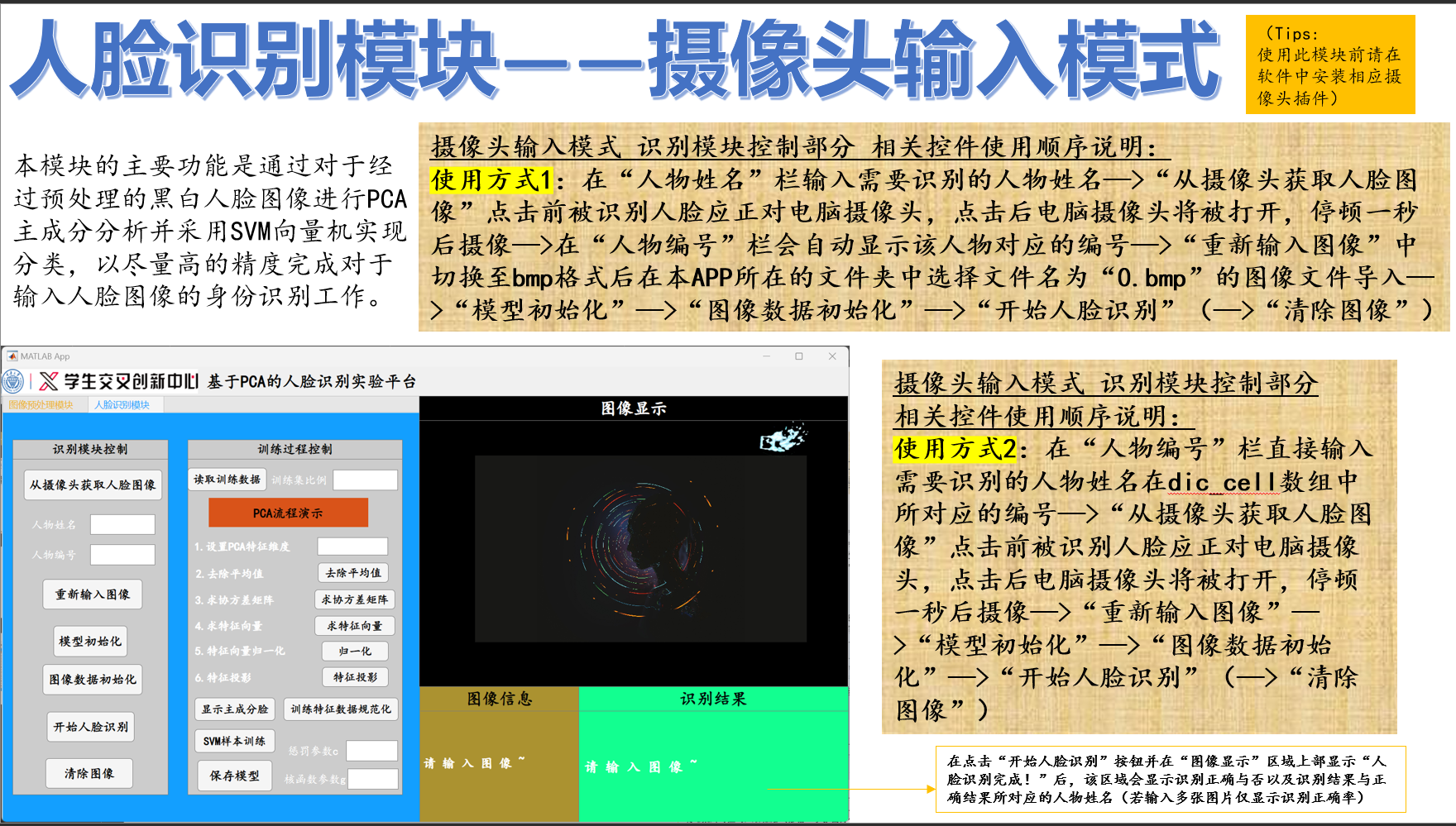
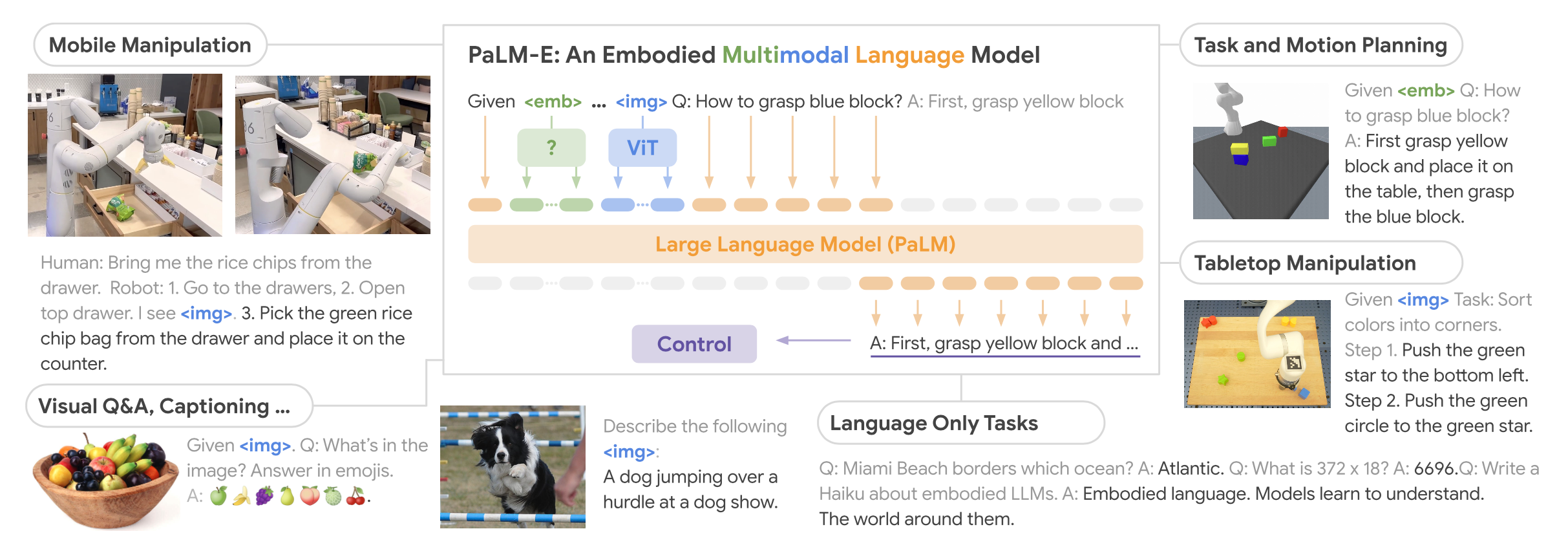
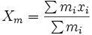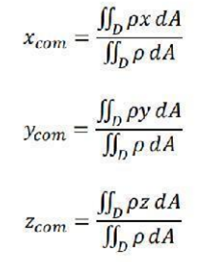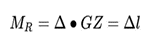本项目定量分析部分Matlab代码已同步上传至Github,仓库链接:Asgard-Tim/QEA-Boat: 重庆大学明月科创实验班定量工程设计方法课程项目 (github.com)
一、项目介绍 在该项目中,我们需要设计制造一艘小船,该小船需要满足以下条件:该艘船的倾覆角度须满足在120°至140°的范围之内,即在倾斜角度到达120°之前都能够回正,同时在超过140°之后不再具有扶正的能力;此外,船体具备一定的载重能力(两罐听装可乐),不会沉没或者有太大(平衡位置甲板与水面夹角超过10°的倾斜)。为了达到以上的指标要求,我们将使用Matlab软件进行相应的定量分析设计,并以木板为材料进行加工制作。具体的呈现详见下文。
二、第一性原理分析
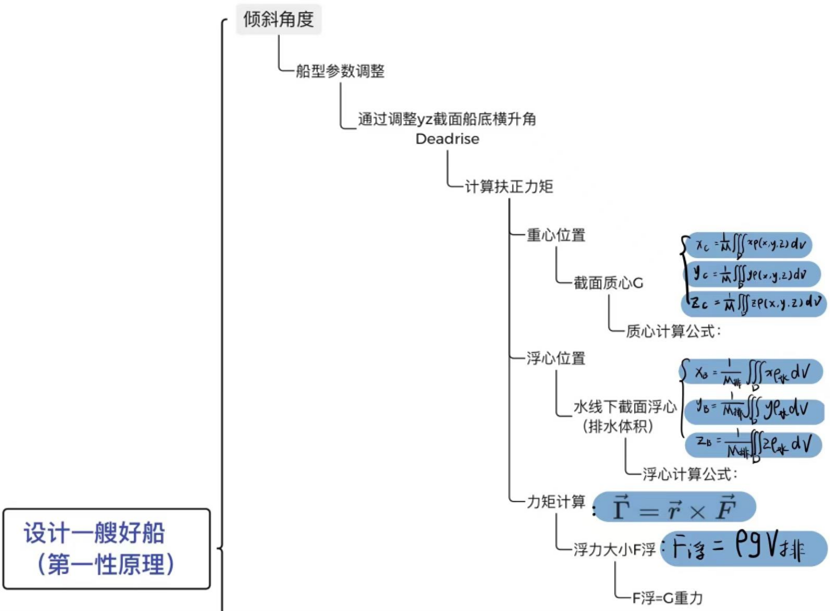
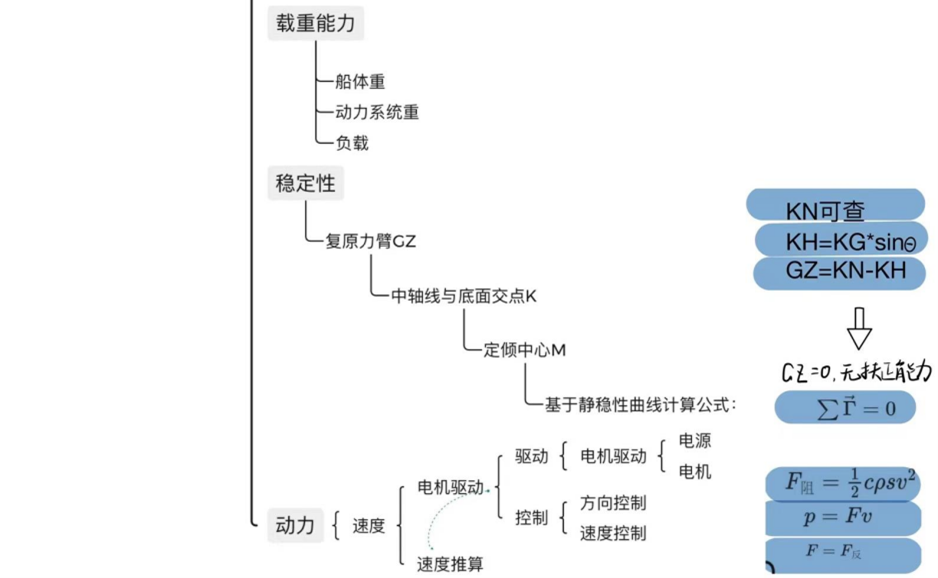
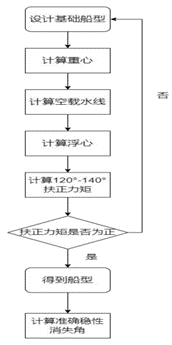
在明确需要达成的指标之后,我们需要使用第一性原理对需要解决的问题进行回归、逐层拨开,回到基本的数学物理公式之中,以便进行较为精确的定量化设计。深入过程见上图。
三、船体设计 3.1设计方向 3.1.1第一性原理的实现 倾覆角度(120°~140°)实现:
设计灵感来源于鱼漂(鱼漂主要分为漂尾、漂身、漂脚,三部分。漂脚大致分为碳脚、竹脚、钢脚等,漂脚的材质不同,自身的重量就不相同,漂脚越重整支鱼漂的重心就会偏下,使鱼漂入水后翻身站立的时间缩短,也就是我们常说的翻身快。)鱼漂的结构恰好可以很好地解决90°以上倾覆角回正的问题,即“头轻脚重”。通过为船体加装舰岛等提供浮力的模块以及合理调节船体各部分高度来进一步精确化满足倾覆角区间。
载重能力(约700g)实现:
除去船体本身的重量将实现700g左右的载重。船体设计将在船体舰岛中为所载货物预留空间,并且预留出排水体积(即预留最大吃水深度),以满足载重要求。
稳定性实现:
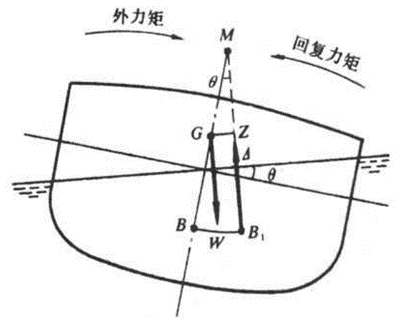
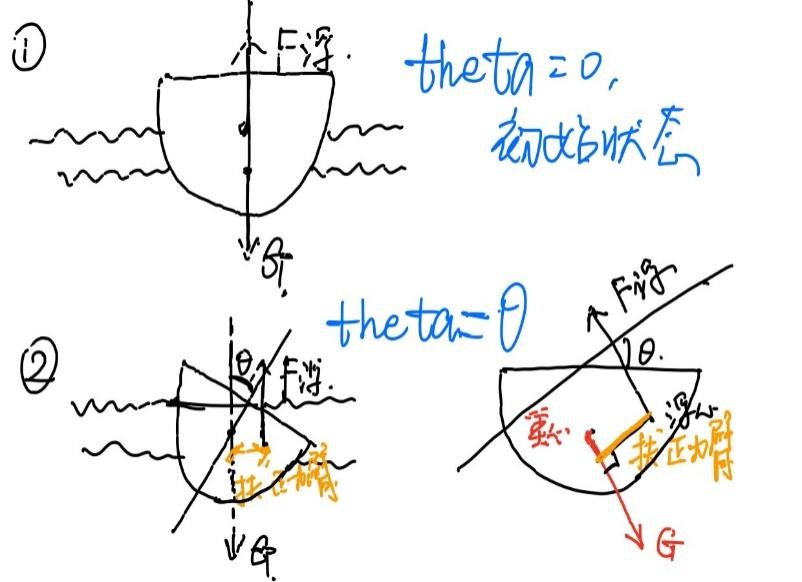
当船舶受到外力倾斜时,其重力的大小位置不发生变化,浮力的大小也不变,但浮力的中心位置会发生偏移。我们知道浮力作用的中心是水下体积的中心,当船舶倾斜时,水下体积形状发生改变,倾斜下沉一侧的水下体积会增加,此时浮力的作用中心会向倾斜的一侧移动,浮力和重力不在同一条直线上,他们形成的力矩和倾斜力矩相反,这就是船舶的复原力矩。只要船舶倾斜,船舶的复原力矩就必然出现,方向永远和船舶的倾斜方向相反,这就是船舶拥有稳性的原因。我们将船舶这种受到外力矩(如风浪等)的作用而发生倾斜,在外力矩消失后自行恢复到原来平衡位置的能力,称为船舶的稳性。
我们对船的剖面演示分析可以发现。当船发生倾斜时,浮心位置改变,我们将浮心所在的垂线于船体中心线交点称为稳心。当稳心在船舶的重心之上时,船舶可以回正。当稳心在重心之下,船舶就发生了倾覆。那么船舶横摇的角度达到多大的时候,我们的船会发生倾覆呢?我们分析研究稳性力臂随着船身倾斜角度变化的曲线。当稳心与重心等高时,也就是这条曲线由正变为负的时候,所对应的船身倾斜角度叫做稳性消失角。当船体的倾斜超过了这个角度,船就会翻。也就是说船舶倾斜在稳性消失角之前,稳心的位置比重心高,稳性力臂为正,复原力矩值也就为正,这时即使船体倾斜,也会回复到船舶原有的平衡位置。当船舶倾斜角度超过了这个稳性消失角,稳心位置就比重心低,稳性力臂比为负,复原力矩值也就为负数,那么这个时候就会发生翻船。这样就解释了船受到外力作用会在海中左右摇摆,随着外力的增加摇摆的更加激烈,船的横摇由于复原力矩的存在,能使其回正,但若超过了稳定消失角这个值,就会发生倾覆。
提高船体稳定性一是降低船体的重心来提高船舶的稳性。例如比赛帆船,通过加中竖龙骨的方法来降低它的重心,使其稳性消失角能够达到150度~170度的角度,接近于永不颠覆的船。另外,增加船宽也可以使船舶获得更高的稳性。例如对安全性要求较高的原油运输船,船体会比较宽,船型比较的矮胖。其他还有多种方式可以抵御船舶倾覆的风险。
动力实现:
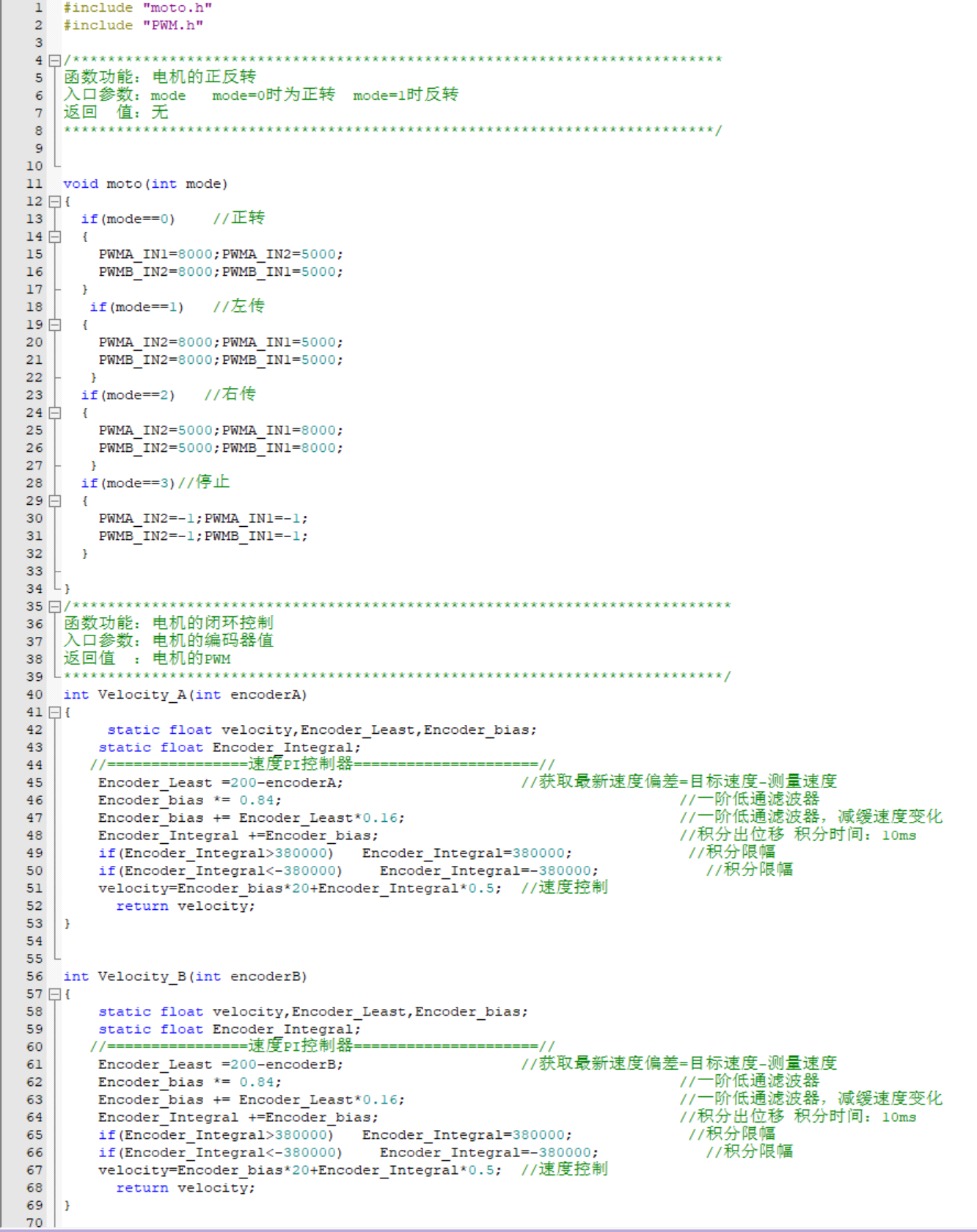
动力大致分为驱动和电控两个模块,以及电池,螺旋桨的装配,选取适当控制模块来实现。
3.1.2船体造型与其他功能的实现 本次项目设计船舶计划设计类似军舰外形的船体,并且达到船体轻巧,航速较快的目标,在此基础上可以实现节能,造价低廉的非硬性目标。
3.2船体初步设计方案
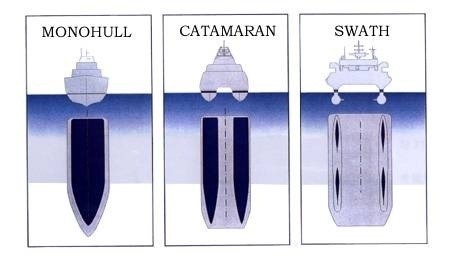
根据本次项目要求以及船型设计初衷(类军舰)采用了以上减小阻力的第一种设计类型,即通过收窄船体且前尖后宽的方式。
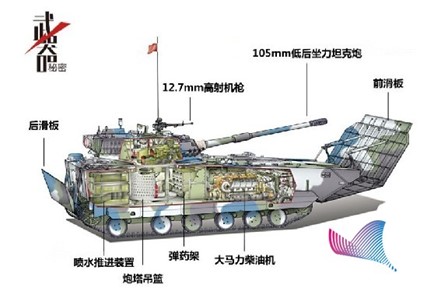
船头借鉴了05式两栖装甲突击车前减阻板的结构,并与上图传统船型结合的联合减租模型。
关于中国05式两栖装甲突击车
新型国产高速两栖突击车首先列装海军陆战队,已经成为海军利器。它不但能在摇摆的海上,精准摧毁敌方阵地工事,而且其强大的威力足以摧毁各型主战坦克。中国05式两栖突击车,操作简单,已没有离合器,具备浮渡精准射击能力。
简介
ZBD-05两栖步兵战车又被称为05式两栖步兵战车,是中华人民共和国研制的”05式两栖装甲车族 “一员,装备中国人民解放军海军陆战队 和陆军两栖机械化部队的滑水型高速两栖装甲车辆,部分言论称它与美国海军陆战队 的”远征战斗车”(Expeditionary Fighting Vehicle, EFV)在概念上相似。
评价
该车外形新颖,车体前部的防浪板是带加强筋的,不但外形宽大而且具有液压伸直调节功能,可以根据海浪的高低和需要的航速自行调节其前倾角度,这就使得整个车体具有了滑行板的功能,在水中行驶时,通过滑行板将水的浮力和速度转化为上抬的力量,类似快艇一样,可以将整个车体短时抬离水面,降低阻力,提高速度。车体前后的防浪板再加上车体两侧打开的侧裙板,可以使得整个车体和水的接触面积大大增加,既增加了该型车在航渡中的稳定性和安全性,还能使得大口径武器如轻型坦克 上的105mm火炮具有了在航渡过程中随时可以开火而不致翻沉。在正常陆战使用中,防浪板和后调节板收回车体,还能起到装甲防护的作用。
总结
05式两栖突击车独特巧妙的外形设计是它能快速机动的重要原因。车体前后部的防浪板外形宽大,能根据海浪的高低和需要的航速自行调节前倾角度。突击车在水中行驶时,防浪板将水的浮力转化为向上的力量,再配合车体两侧打开的侧裙板,将突击车短时抬离水面,从而大大降低阻力,提高速度。
舰岛部分以空心提供浮力为主,辅助来进行大角度回调。
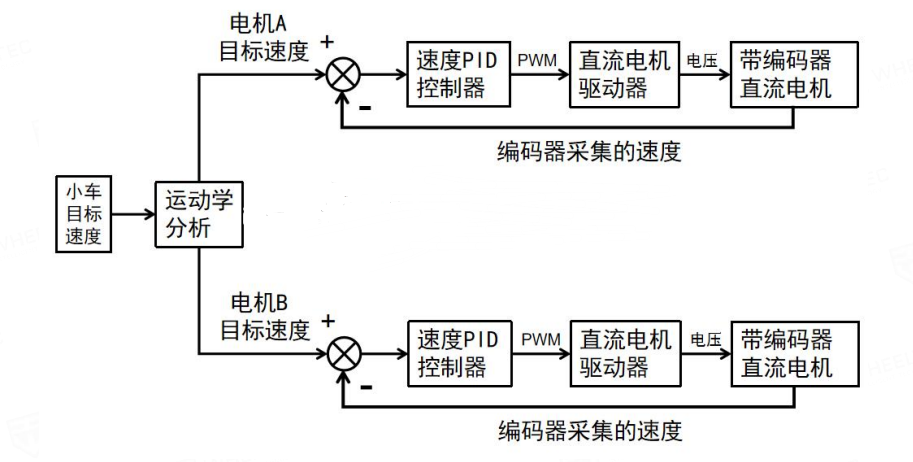
驱动控制部分设计为电路模块,包括信号揭发部分,电动机控制部分;驱动模块包括电子调速器,电动机,螺旋桨模块以及锂电池。行进方式采用双桨无舵型,以两个推进器的差速法控制船体行进方向。
※具体实现以及其他细节后续介绍这里不再给出
四、程序定量设计 4.1 量化指标的数学物理分析 基于上述对实际问题的第一性原理分析后,我们不难得出,要使得负有一定载重的船体呈现出满足要求的扶正能力,关键在于对于船体稳定性的量化考察与计算。具体而言,我们可以通过重心、浮心、扶正力矩与稳性消失角等一系列量化参数对于船体的扶正能力进行进一步的定量描述,并根据定量分析结果调整船体设计使其具有相应的扶正能力。
4.1.1 重心 重心(Centroids)即为重力中心,本质上是物体在重力场中所受重力作用的等效作用点。在对于船体扶正能力的定量分析中,我们需要通过物体重心与浮心的位置关系判断扶正力矩的正负从而得到稳性消失角以衡量船体的扶正能力。
事实上,由于实验环境处于重力场相对均匀的地表,重心和质心(Center of Mass)在误差允许范围之内可视为重合,因此在定量计算时,我们实际上是将重心等效于质心,通过对于船体质量中心的计算间接得到重力中心的三维坐标。
在上述理论事实的支撑下,我们成功地将问题转化为“如何求取物体质量中心”。不可忽略的一点是,在实际定量计算中,对于物体质量中心的求取首先要将整个物体进行离散化处理,即将物体视作由许多质点组成的质点系,再对这些离散的点进行处理;同时,由于项目中的船体负有载重,离散化的质点系处理过程还便于额外添加船体外壳之外的其他额外质量点(如配重的质心等)。因此,控制物体离散化(本质上是从x,y,z三个方向进行微分)的精度是使得质心坐标结果更为精确的重要一环。在离散化的基础之上,对于N(该项目中N=3)维空间中的质点系而言,在坐标系中有以下质量中心坐标计算公式:
其中X表示某一坐标轴;mi表示物质系统中,某i质点的质量;xi表示物质系统中,某i质点的坐标。
而具体到本项目中所处的三维环境下,又有如下更为细化的公式:
其中,x(y,z)为各坐标轴下质点分布的方程,ρ为船体材料的密度,dA为微分后每一小块的体积。
通过这一公式,就可以得出三维空间中物体离散化后的质点系的质量中心坐标。当离散化程度足够(微分步长足够小)时,在地表实验环境下,这一坐标同时也就是物体重心的坐标。
4.1.2 浮心 浮心(Center of Buoyancy)是指浮体或潜体水下部分体积的形心,本质上是浮力的等效作用点。当浮体方位在铅直面内发生偏转时,其水下部分的体积虽保持不变,但其形状却发生变化,因而浮心的位置也相应的移动。在对于船体扶正能力的定量分析中,我们需要通过物体重心与浮心的位置关系判断扶正力矩的正负从而得到稳性消失角以衡量船体的扶正能力。
当物体放入流体中时,由于物体与流体的上下接触面受到流体的压强不等,上小下大,故会产生压强差,进而物体会受到流体竖直向上的压力,即受到流体的浮力。依据阿基米德定律,可得出物体受浮力大小为物体排开那部分流体所受到的重力。自然的,浮心的位置即为被排开流体部分的重心位置。若被排开流体的几何形状是规则的,那么浮心就在被排开的流体原先的几何中心。
事实上,在不同的倾斜角度情况下,物体在水下部分的形状都各不相同,因此随着倾斜角度的改变,浮心也在时刻发生着改变。而在某一固定倾斜角度时,对于浮心的求取本质上即为对于物体排开部分的水的重心求取。在上一节中我们详细阐述了如何计算物体的重心,只是在这里我们需要在不同的倾斜角度下分别求取水下部分的重心,具体计算原理完全一致,在此不过多赘述。但在浮心求取中涉及到的另一个问题是,应该如何确定船体水下部分的船体形状呢?在这里,我们引入水线的概念,即对于船体截面而言,水下部分与水上部分的分界线。上面提到,随着倾斜角度的改变,尽管排开水体部分的形状不尽相同,但提供的浮力大小一致,由阿基米德原理不难得出,即排开水的体积始终不变。因此,我们可以依据这条原理,得到各倾斜角度下水线的方程,与船体截面方程在水线之下的部分共同框定水下部分的形状,从而进行浮心的计算。
4.1.3 扶正力臂(矩)与稳性消失角 船的稳性消失角(AVS)是角度θ,当船体的倾斜角度达到该角度后,船体就会倾覆而不再能够自动回倾。利用前两节给出的方法,我们可以得到船体的重心与浮心坐标,它们同时也是重力与浮力作用在船体上的等效作用点。而在这两个力的作用下,会对船体产生一个由重心与浮心之间的距离创建的力矩臂,浮力作用在该臂上以产生扭矩。随着倾斜角度的改变,扭矩的大小与正负也在不断改变,这里不妨规定船体扶正的力矩方向为正。在倾斜角度增大的过程中,力矩臂从正到负,而船体则在力矩臂由正转负的转折点时达到其AVS从而倾覆。当这一浮力产生的扭矩能够使得船体回到稳定平衡的原始位置时,它就是扶正力矩。为此,重心与浮心必须大致满足垂直对齐。如果这两个点稍微偏离对齐状态,则会产生一个扶正扭矩,将两个点推回到对齐状态。两点对齐的下一个可能角度是不稳定的平衡,这意味着如果稍微偏移,系统将无法恢复到其原始状态。当系统稍微偏离不稳定的平衡状态时,所产生的扭矩将改变角度,以使两点变得更加偏离对齐状态。
基于上述对于扶正力矩的定义阐述与分析,我们可以得出以下公式:
式中的GZ为重力作用线与浮力作用线的垂直距离,称为扶正力臂;而MR则为扶正力矩。
扶正力矩与扶正力臂在受力分析图中的呈现如下图所示:
上述分析中提到,稳性消失角仅仅与扶正力矩由正转负的过程有关。通过对于上述式子的观察,不难发现,由于船体扶正或倾覆仅仅取决于扶正力矩的正负,而该计算式中扶正力矩的正负仅仅由扶正力臂的正负所决定,因此基于我们的分析需求,要得到稳性消失角以衡量扶正能力,只需要关注扶正力臂的正负而不关心具体的数值大小,事实上由公式可知扶正力矩只是在扶正力臂的基础上乘上了恒为正的系数(浮力大小)。于是,关键即在于对于坐标系中扶正力臂的求取。具体到坐标系中扶正力臂的计算公式会在后续Matlab程序仿真实现时详细推导与阐述,在此不详细展开。
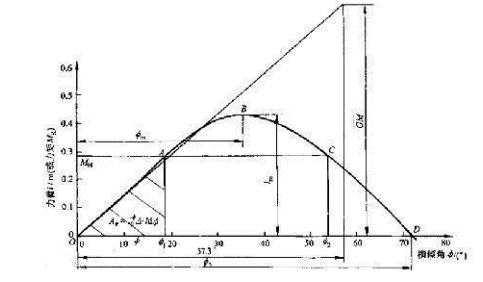
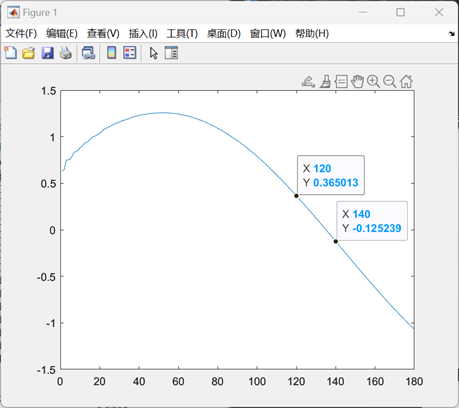
对于不同的倾斜角度而言,由于淹没部分的形状不同导致浮心位置不同,扶正力臂的大小和正负自然也不同。因此,为了得到稳性消失角,我们可以通过绘制不同倾斜角度下的扶正力臂数值图像,从而得出图像零点处的倾斜角度(横坐标)即为稳性消失角(如下图)。
4.2船体模型构建与仿真模拟 4.2.1设计思路 基于以上数学物理分析,结合定量分析的需求,我们制定如下设计流程:
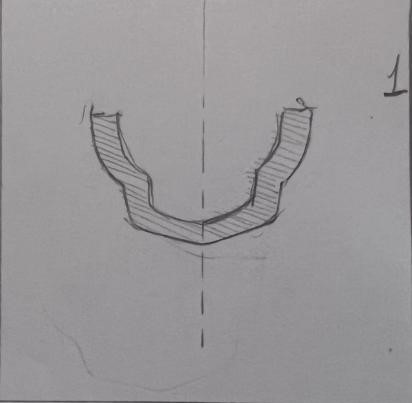
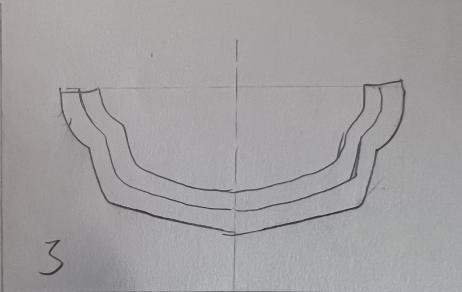
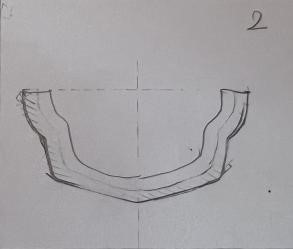
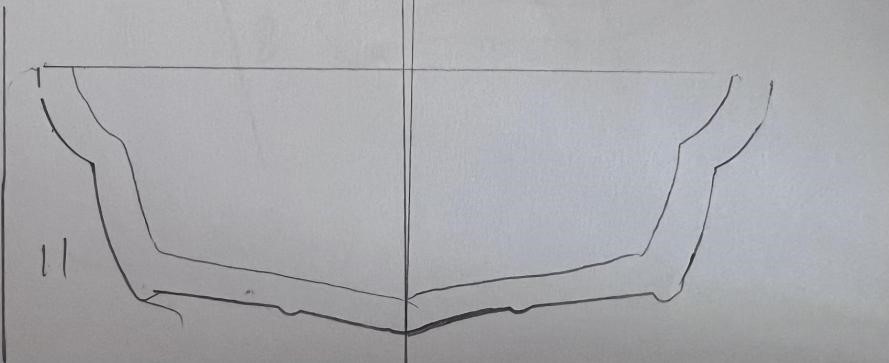
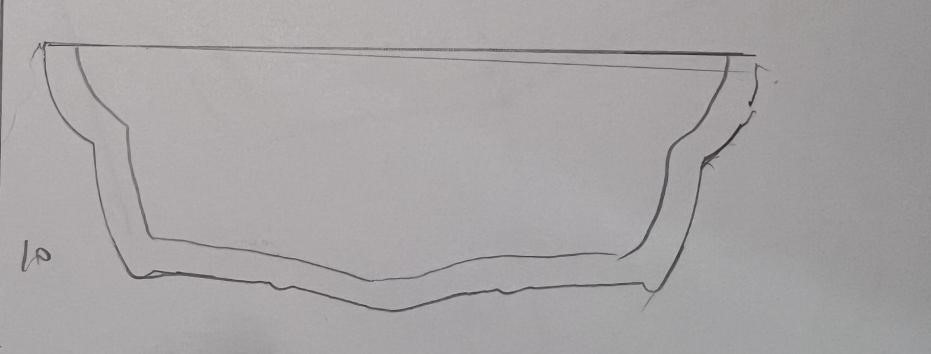
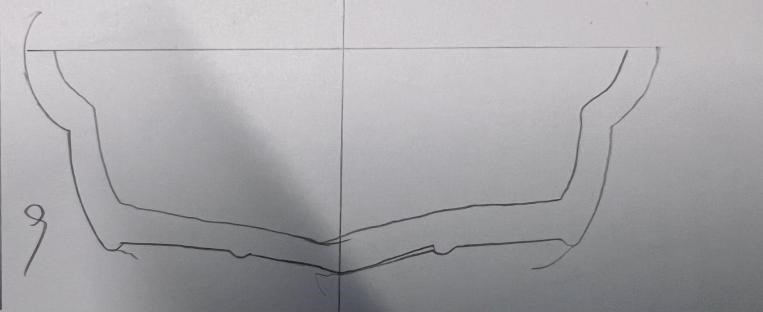
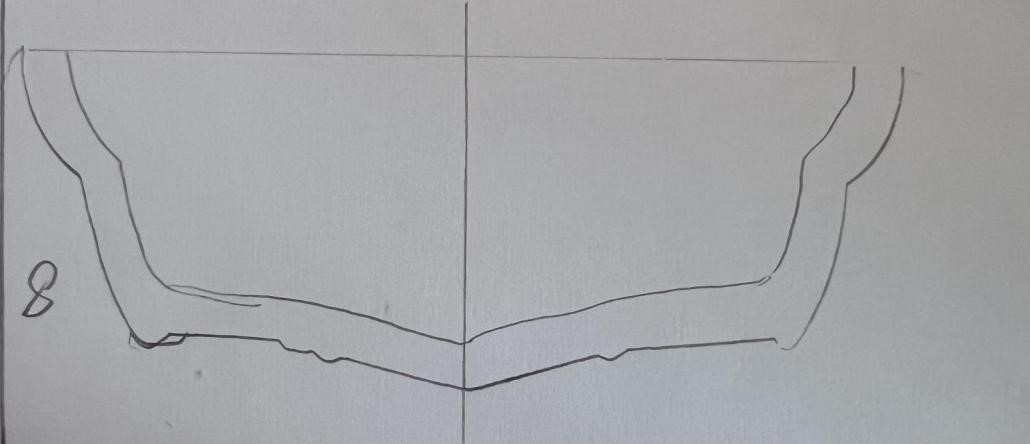
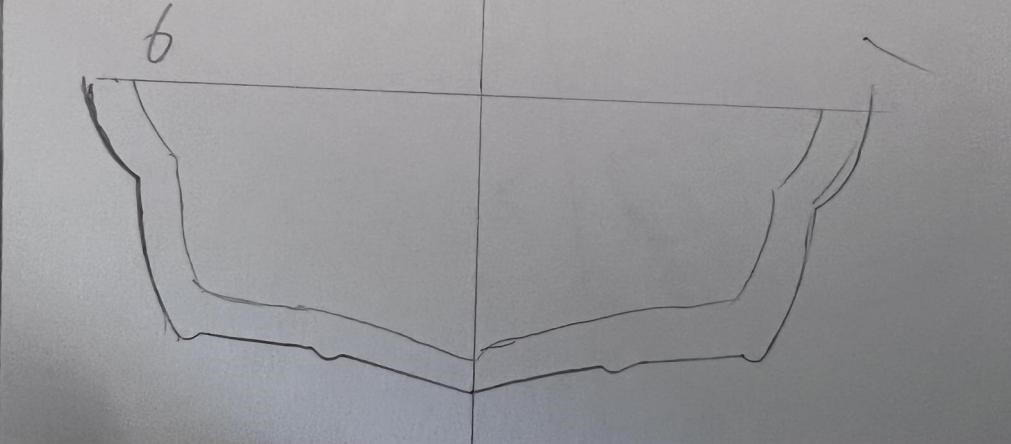
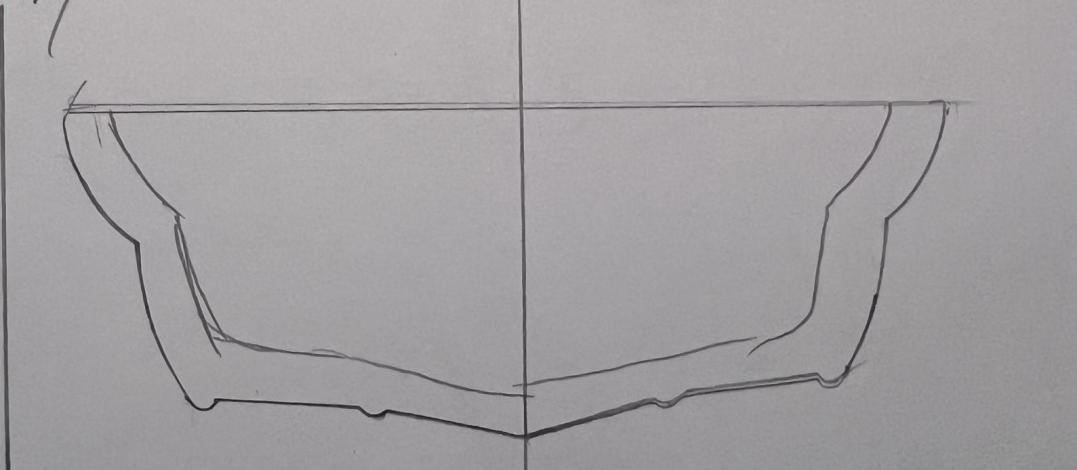
具体到实际的设计流程中,我们考虑到如下事实:当船底形状越平,该船的重心越低,船在载重的时候越不容易倾斜,船的平衡性更好。因此,我们基于以上原理,首先通过设计手绘图纸(见附件:切片.docx)的形式确定每一个切片(即船体沿长度方向的横截面)的轮廓形状,然后将切片以草图的形式在Fusion360建模软件中进行绘制,再对各切片草图进行放样操作即可得到船体外壳建模模型;在建模的草图绘制过程中,同时又在y(宽度)方向以一定步长进行采样,得到一系列离散坐标点,从而导入Matlab中进行进一步的仿真定量分析,最终得到符合要求的稳性消失角。
4.2.2基于Fusion 360软件实现船体建模 具体实现步骤如下:
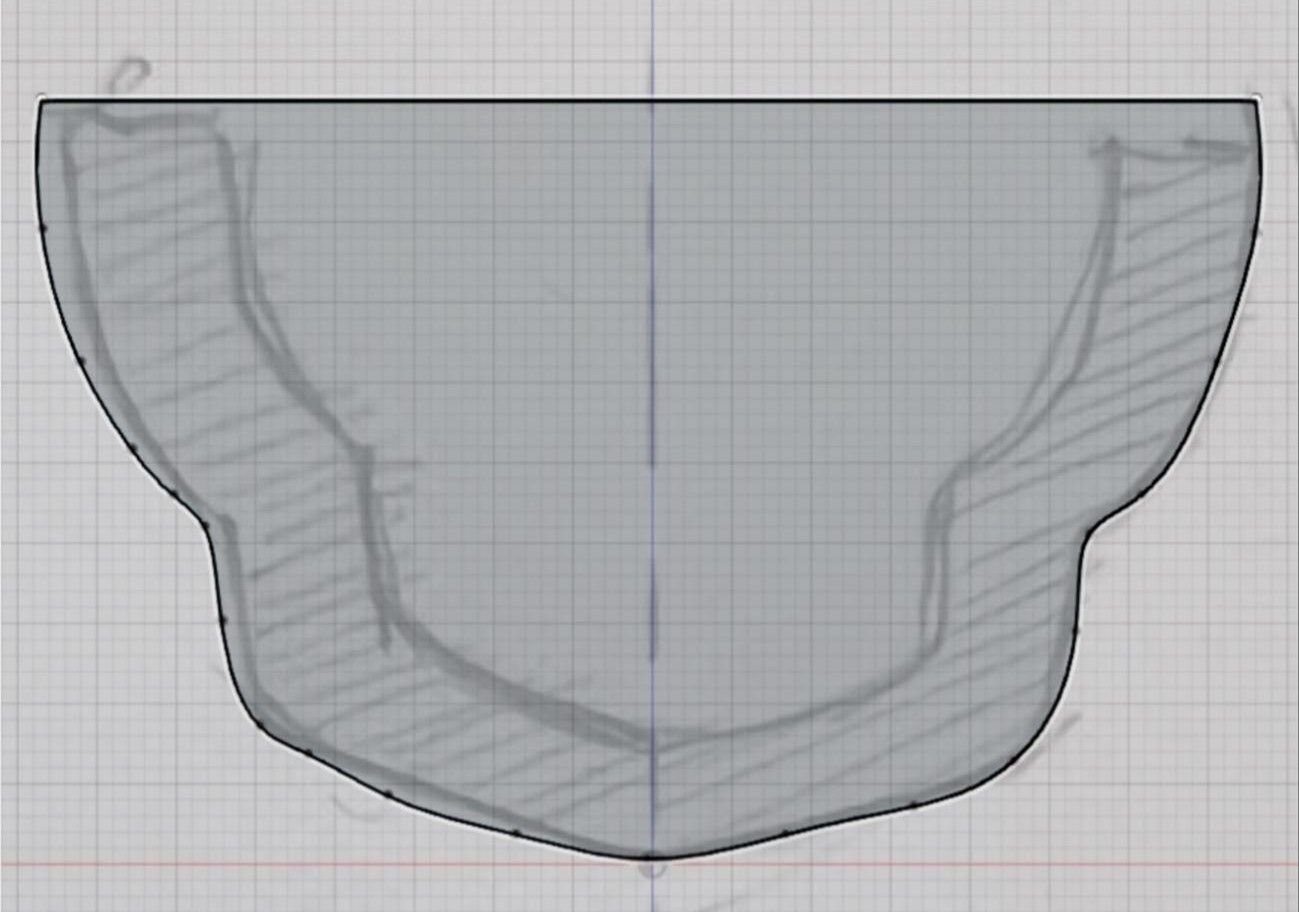
将绘制的切片曲线草图依次插入作为画布,并根据草图轮廓(适当修正)利用多点曲线拟合工具得到每一个切片的草图(如下图),各切片之间相隔特定的长度。
在绘制草图曲线的过程中,对于拟合后的放样曲线在宽度方向上以0.5cm为步长进行采样,结合各切片所在的长度坐标可得到船体的点云数据(详见附件our boat.xlsx),以供后续Matlab仿真处理。
切换至曲面工具,对得到的每一个切片草图的曲线轮廓进行放样操作,得到船体模型大致的表面曲线;再修改选择使用曲面切线,使得曲线更加符合设计草图并更加自然流畅;最后进行封顶,完成船体外形的大致建构。
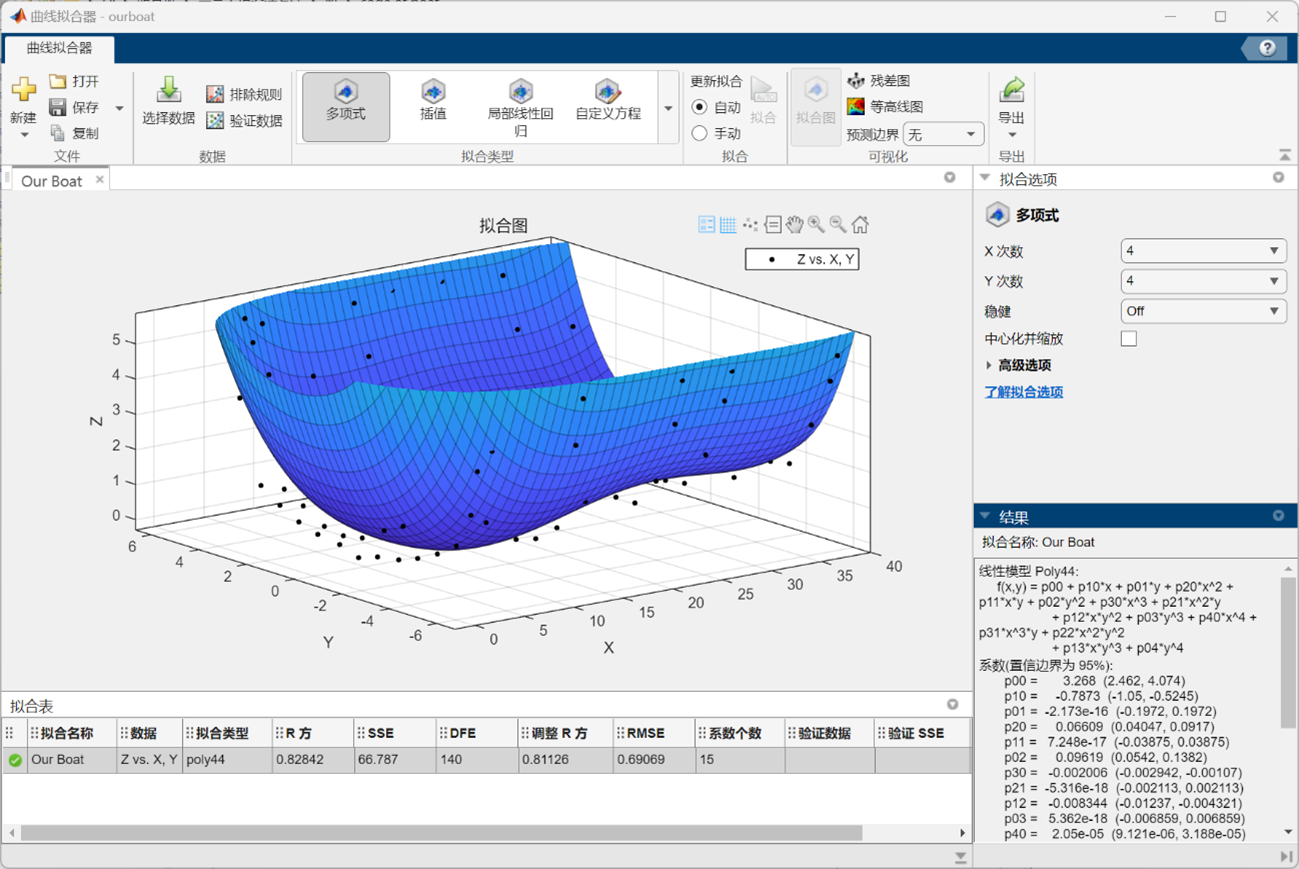
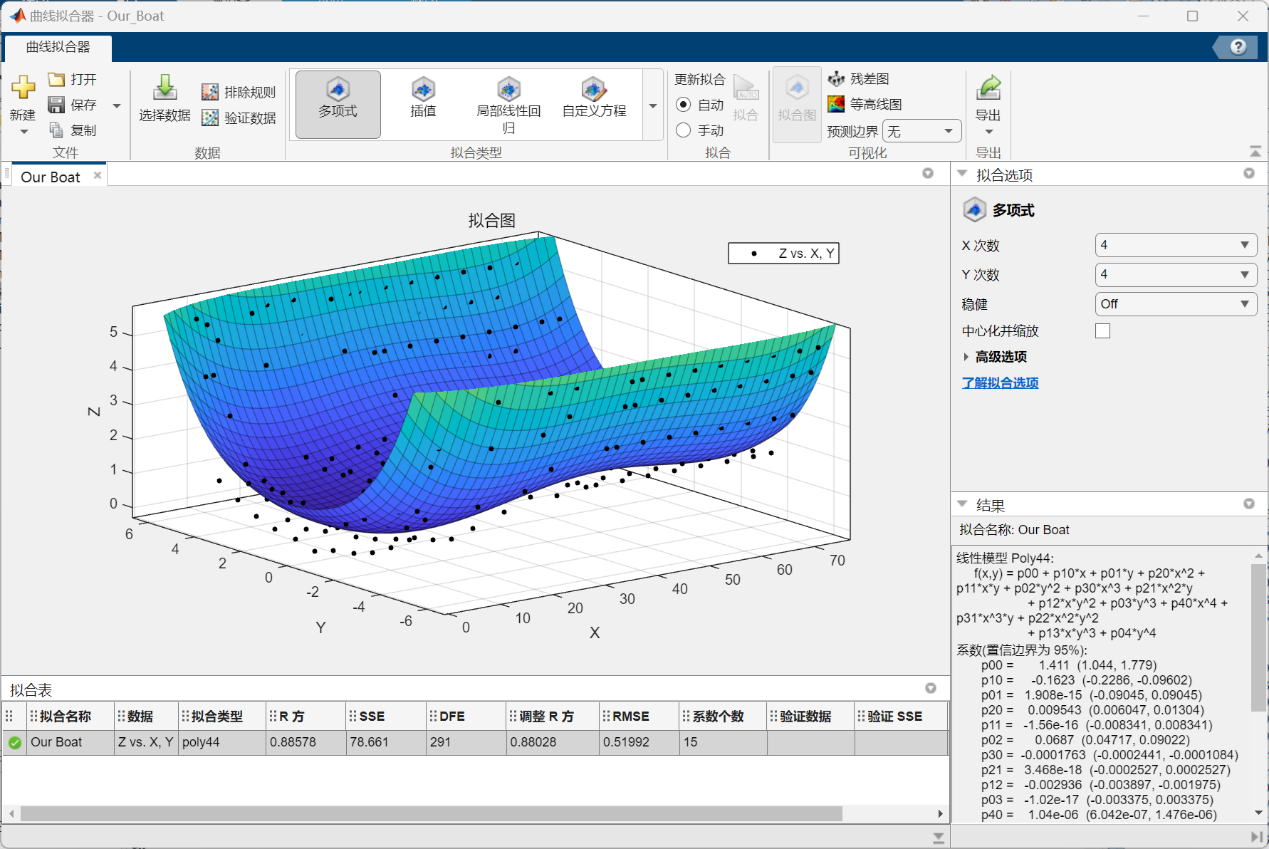
4.2.3基于Matlab软件构造船体外壳曲面数学模型 通过上述利用Fusion360进行的建模过程,我们成功地将切片的草图实体化成了3D模型,并在这一过程中获得了点云数据坐标。接下来,我们将记录在excel表格中的x、y、z点云坐标分别导入Matlab中的mat文件并命名为“X.mat”、“Y.mat”和“Z.mat”存储下来。随后,通过load命令将三个数据文件导入Matlab中的工作区,并利用cftool指令使用曲线拟合器,分别选择X、Y、Z数据,通过多项式对点云数据进行拟合,效果如下图所示。(详情见文件”ourboat.sfit”)
值得注意的是,在点云的获取过程中,我们以船体最下方的点在船体前端的投影作为坐标原点,以船体的长度方向作为x轴,由船头向船尾延伸;船体的宽度方向为y轴,以船的中轴线为分界线,沿x正方向看去左边y值为负,右边y值为正;船底到船顶为z轴正方向。
将所得到的拟合图与建构出的3D模型进行对比,除去比例尺的因素外,外壳形状基本一致,说明模型建构有效,数据与拟合函数可信度高,可以进行下一步仿真。在验证数据有效性的同时,我们也得到了拟合出的曲面函数(如图中右下“结果”框图所示),将其存于函数文件“calculate.m”中,便于后续仿真验证时进行调用。
除此之外,在仿真验证的程序中,我们在导入点集数据之外还需要对船体的各项参数进行定义,并给出微分步长,同时对已有的点集数据进行适当的处理使结果更加合理。
下面给出船体数学模型建立部分的Matlab实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 load('X.mat' ); load('Y.mat' ); load('Z.mat' ); boat.L =39.9 ; boat.W = 17.4 ; boat.HB = boat.W / 2 ; boat.D = 5.4 ; density_water = 1 ; boat.mass = 2000 ; num=100 ; dy = boat.W/num; dz = boat.D/num; dx = boat.L/num; mesh.xs = 0 :dx:boat.L; mesh.ys = -boat.HB:dy:boat.HB; mesh.zs = 0 :dz:boat.D; [mesh.ygrid,mesh.zgrid] = meshgrid (mesh.ys,mesh.zs); [Xi,Yi]=meshgrid (mesh.xs,mesh.ys); Zi=griddata(X,Y,Z, Xi,Yi); surf(Xi,Yi,Zi); shading flat; axis('equal' );
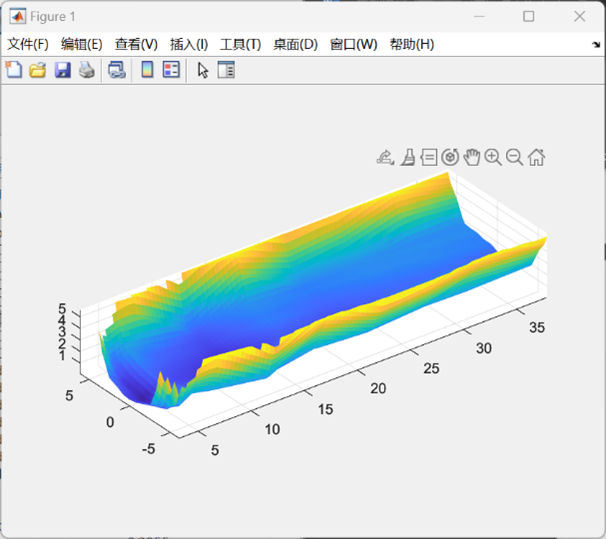
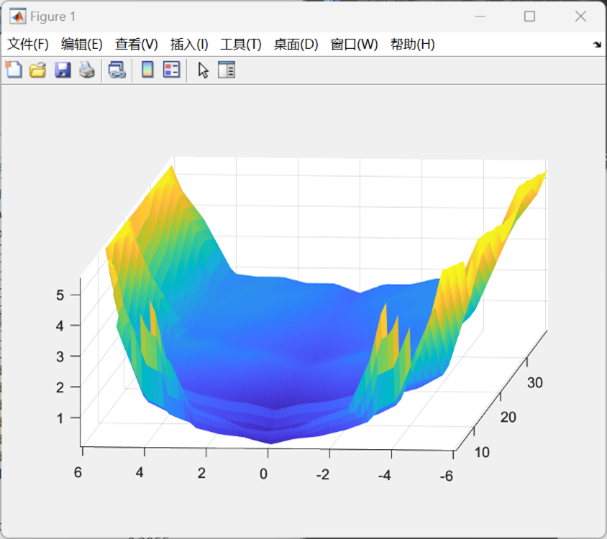
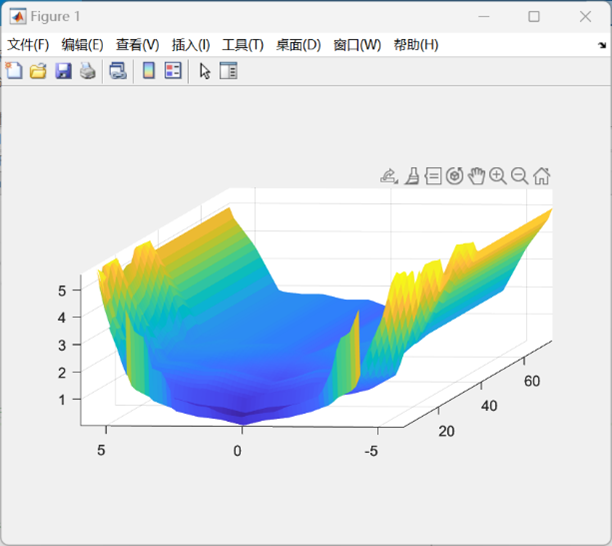
在这里,我们运用了griddata插值函数,对于取样的点云进行了进一步的补充,使得拟合的函数模型曲面更接近于实际情况。所得到的船体曲面模型如下图所示。
至此,我们成功地在Matlab中对我们设计的船体进行了数学函数的拟合,并通过对于函数图像的绘制模拟出船体的外壳模型,同时在程序中对于船体的点云数据以及宏观参数与微分步长都进行了导入与定义,为后续的仿真过程做好准备。
4.2.4船体重心与浮心三维坐标计算及其Matlab实现 重心计算 :在前面的原理分析部分,我们已经给出物体重心的详细计算方法。
下面给出了Matlab中的实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 COM_x=0 ; COM_y=0 ; COM_z=0 ; tnt=0 ; i =find (isnan (Zi));Zi(i )=0 ; for i =1 :num for j =1 :num COM_x=COM_x+Xi(i ,j ); COM_y=COM_y+Yi(i ,j ); COM_z=COM_z+Zi(i ,j ); tnt=tnt+1 ; end end m1=500 ; boat.finalmass=boat.mass+m1; x1=10 ; y1=0 ; z1=1 ; m2=500 ; boat.finalmass=boat.finalmass+m2; x2=30 ; y2=0 ; z2=1 ; m3=1000 ; boat.finalmass=boat.finalmass+m3; x3=20 ; y3=0 ; z3=8 ; density=boat.mass/tnt; COM_x=(COM_x*density+m1*x1+m2*x2+m3*x3)/boat.finalmass; COM_y=(COM_y*density+m1*y1+m2*y2+m3*y3)/boat.finalmass; COM_z=(COM_z*density+m1*z1+m2*z2+m3*z3)/boat.finalmass;
通过运行上述程序,我们可以得到我们设计的船在加上配重与桅杆后的最终重心坐标为:
各倾角下浮心计算 :在原理分析部分我们提到,船体的浮心位置会随倾斜角度的改变而不断改变。结合我们在获取稳性消失角时的绘图需求,我们采用循环结构,对从0度到180的所有倾斜角度进行遍历,分别求出各角度下的浮心坐标。
以下是浮心三维坐标计算的Matlab实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 COB_x=[]; COB_y=[]; COB_z=[]; MMass=[]; tot_mass=0 ; Y=[]; for theta=1 :1 :180 for i =1 :num ZZ=[]; for j =1 :num+1 t=calculate(i *dx,mesh.ys(1 ,j )); ZZ=[ZZ t]; end boat.hull = mesh.zgrid > ZZ; d =water_line(mesh,theta,boat,dx,dy,dz,num); y = mesh.ys; z = -tand (theta).*y+d; if theta>90 && theta<=180 water = (mesh.zgrid-boat.D/2 ) < z; elseif theta<=90 && theta>=0 water = (mesh.zgrid-boat.D/2 ) > z; end sub_region = flipud (boat.hull)&water; COB = centerOfMass2(sub_region,mesh); COB_z=[COB_z COB(1 ,2 )]; COB_y=[COB_y COB(1 ,1 )]; COB_x=[COB_x i *dx]; MMass=[MMass matrixSum(sub_region)]; tot_mass=tot_mass+matrixSum(sub_region); end ANS=centerOfMass3(COB_x,COB_y,COB_z,MMass,tot_mass,num); COB_x=ANS(1 ,1 ); COB_y=ANS(1 ,2 ); COB_z=ANS(1 ,3 );
从而我们可以得到不同倾斜角度theta下的浮心三维坐标。
在上述计算浮心的程序实现中,事实上我们是对于整个船体的浮心进行了整体的求取,具体而言是将船体沿x轴(长度)方向以一定步长微分为num(船体模型建构程序段中有给出定义,是微分的分数)份切片,每一片都分别求取重心的y-z坐标并最终沿x轴方向叠加得到整个船体的浮心。
具体到对于每一个切片的浮心求取,虽然实际情况中是船体在水中倾斜,但为了方便计算,我们不妨处理成船体不动而水线不断改变,当船体的倾斜角度为theta时,水线的斜率应为-tan(theta);同时在计算时,基于浮力大小不变的原则,即船体淹没部分的体积不变,可以通过函数water_line进行迭代从而得到水线在船体切片的二维y-z坐标系的截距(在数据处理上对于迭代次数与精度进行限制以节约计算时间)。经过上述处理,我们可以得到各倾斜角度theta下各个切片平面中的水线方程。值得注意的是,这里为了使结果更加精确,我们将各点的x,y坐标重新带入了建构模型时所得到的calculate函数从而得到与实际更加接近的z值坐标,并以此来框定各个切片下的函数方程描述。在原理分析部分提到,在某一切片平面中,水线与水线之下的船体函数共同框定了水体淹没面积,对这一部分进行重心的求取即为切片的浮心。
下面给出water_line函数的代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 function D_line = water_line (mesh,theta,boat,dx,dy,dz,num) number = 1 ; i =1 ; d = -0.02 ; d_gap = 0.07 ; density_water = 1000 ; while number<100 y = mesh.ys; z = -tand (theta).*y+d; if theta>90 && theta<=180 water = (mesh.zgrid-boat.D/2 ) < z; elseif theta<=90 && theta>=0 water = (mesh.zgrid-boat.D/2 ) > z; end sub_region = flipud (boat.hull)&water; force=sub_region.*density_water*dz*dy*dx; lift= matrixSum(force); up_force=lift-(boat.finalmass/num); if up_force<0 d=d+d_gap/i ; elseif up_force>0 d=d-d_gap/i ; else break ; end if up_force>-0.01 &&up_force<0.01 break ; end i =i *2 ; number=number+1 ; end D_line = d; End
此处同时展示部分功能函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 function COM = centerOfMass2 (masses,mesh) M = matrixSum(masses); ycom = matrixSum(masses .* mesh.ygrid) / M; zcom = matrixSum(masses .* mesh.zgrid) / M; COM = [ycom,zcom]; end function plotMatrix (A,mesh,cmap) colormap(cmap); image(mesh.ys,mesh.zs,flipud (A),'AlphaData' ,0.5 ); end function M = matrixSum (masses) M = sum(masses(:)); end function ANS =centerOfMass3 (XMass,YMass,ZMass,MMass,m,num) x=0 ; y=0 ; z=0 ; for i =1 :num x=x+XMass(1 ,i )*MMass(1 ,i )/m; y=y+YMass(1 ,i )*MMass(1 ,i )/m; z=z+ZMass(1 ,i )*MMass(1 ,i )/m; end ANS=[x,y,z]; end
4.2.5 船体扶正力臂计算与图像绘制 扶正力臂计算原理与公式推导 :
在原理分析部分中,我们给出了扶正力矩的定义与扶正力臂的图示,并揭示了只需要计算扶正力臂即可通过判断其正负来获得稳性消失角,但并没有给出具体在坐标系中的计算公式。在这里,将进行计算方法的推导并给出扶正力臂的计算公式。
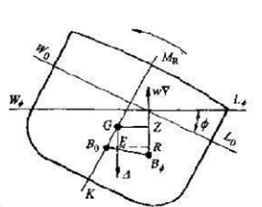
在上述对于浮心坐标求取的代码实现阐述中,我们提出可以将水中船体的倾斜等效为以船体为参考系下水线的旋转。基于这样的分析思路,我们给出了如下左图所示的示意图,以对于扶正力臂的计算进行进一步的推导。
值得注意的是,尽管图中所表示的仅仅是船体的一个截面,但在实际情况中,若船体在无干扰情况下能稳定在水中平稳漂浮,船体重心与浮心的x坐标在误差允许范围内应可以视为一致,因此在仿真计算中,我们暂时忽略重心与浮心的x坐标而仅仅关心两者的位置关系及这一关系在y-z坐标上的体现。
基于这样的分析,结合上述图示,我们不难得出如上右图所示公式。
另外,所谓扶正力矩必然能够使得船体回正而非倾覆,这就要求力矩的方向应与倾斜角度theta增加的方向相反,因此我们不妨规定这一方向为正方向,在图中第二种情况中显示为船体向右(顺时针方向)倾斜,于是扶正力矩(臂)则以逆时针方向为正。基于这一原理,我们给出了如下方法以判定其正负性,这也是得到最终稳性消失角的关键一环。
在完成了上述推导之后,即可根据推导分析结果设计Matlab程序实现仿真验证。
该部分的程序实现代码如下:
1 2 3 4 5 6 7 8 9 10 k1 = -tand (theta); if ((k1*COB_z+COB_y-COM_y)/k1)-COM_z<0 flag1=1 ; else flag1=-1 ; end l = flag1*abs (COB_y+k1*COB_z-k1*COM_z-COM_y)/(k1^2 +1 )^0.5 ; Y=[Y,l]; end
扶正力臂-倾斜角度图像绘制与稳性消失角 :
在扶正力臂的求取部分,我们在不同的theta情况下用矩阵Y来存储各角度下的扶正力臂值,以便于绘制θ-l图像,从而根据观察图像得出稳性消失角。
以下为该部分代码实现:
1 2 3 4 5 x=1 :1 :180 ; x1=1 :1 :180 ; y1=interp1(x,Y,x1,'spline' ); plot (x1,y1);
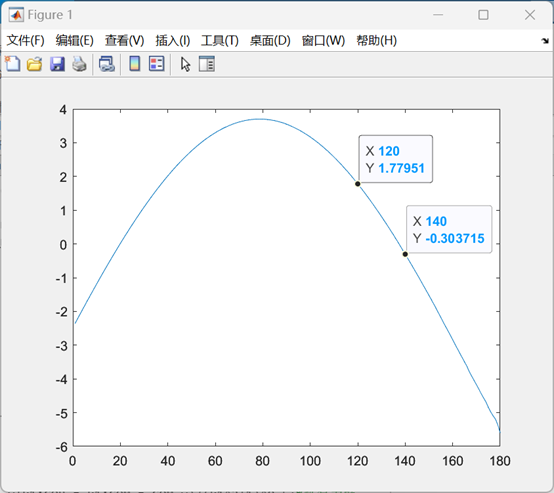
最终得到的图像如下图所示。通过观察图像,可以得到我们的船体模型的稳性消失角大致在120-140度之间,满足稳定性要求。
4.2.6误差分析 (1)采样点云、拟合曲线与实际船体模型的误差 :
由于采样的点云坐标是在对于手绘草图的建模刻画过程中进行读取的,与手绘出的供船体加工的切片草图仍然存在一定的差距,这会带来一定的误差;而在对于点云数据的插值与函数拟合过程中也存在着一定的误差。除此之外,载重的测量误差以及船体在实际加工建造时产生的误差也不可忽略。但由于缺乏一定的工具对于我们建造出的船体实体进行精确的测量与3D模型建构,在数据处理的过程中我们已经对于一些偏差较大的离散点数据进行了纠正或删除处理,使得最终的结果仍然在预期范围之内,并与实际情况相一致。
(2)Matlab仿真时微分步长不足够细分而引起的误差 :
在程序仿真设计过程中,我们对于船体从x、y、z三个方向按一定步长分割为若干份,并重点研究沿x轴方向进行切分的各切片以求得船体的重心与浮心坐标。但在实际程序实现的过程中,考虑到运算速度与准确度等多方面因素,各个方向进行分割的份数num不可能做到逼近于现实的无穷大,在上述程序中我们经过测试得到的一个较为合适的num值为100,这导致我们的仿真计算与实际的情况仍然存在一定的误差。但由于采样点的数量也较为有限,num的有限选取也不会对最终的结果造成致命的影响,仍然可以使得船体的稳性消失角最终呈现在可控的目标范围。
五、 初代船体制造与实现效果5.1 船型外壳5.1.1 结构设计实现为了减轻船体重量,采用了木制板材作为船体材料,通过骨架搭建,外层包裹来实现船模外壳的搭建,过程中主要用到了实木板,白乳胶等材料,加工过程使用绳锯,切割机,打磨机以及电钻等工具。
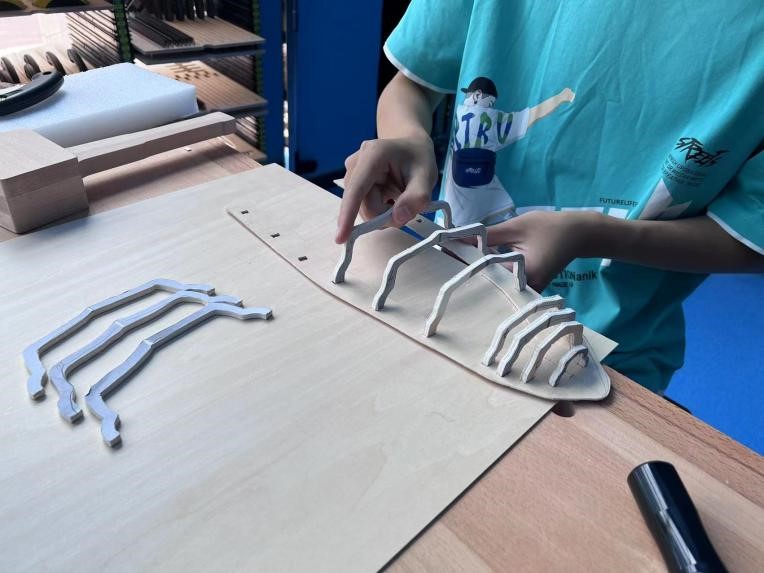
首先,我们根据最初的船体建模,对模型进行切片处理,以此来获得设计船的肋骨图纸和甲板图纸的必要参数,并根据设计出的肋骨图纸以及甲板图纸加工船体骨架,并进行拼装(详见下图)。
然后利用乳胶,热熔胶和木板,将船体外构型粘贴以达到塑性目的。
5.1.2 舰岛设计同样利用模板拼接的方式,构筑舰岛模型。此设计中舰岛的上半部分与下半部分并未粘接,属于分体,用于装载货物使用。
5.2 动力装置
电池:3.5V锂电池
130电机:3.5V 0.7W 双发推力约1.5N
电路板含有电机控制模块(MX1919H实现)与信号接收处理模块。此外设计了对水的感应电路,螺旋桨触水可以遥控发动,离水则发生断路不可发动
螺旋桨部分采用万向结构,这样来减弱偏移对传动的影响。
5.3 防水设计对于船体设计采用了报纸与乳胶混合贴合加固船体的方法,使船体表面硬化并做到初步防水,在彩绘之后涂刷丙烯酸透明防水胶达到更高水平的防水效果。
*船舶防水涂料的应用止水胶防水施工技术。止水胶是一种单组分,无溶剂,遇水膨胀的聚氨酯类无定型膏体,在隧道二次初砌施工缝处设止水胶防水带,以及在钢筋,管线等周围设置止水胶,当接缝中有水渗入时,止水胶的弹性压缩应力和遇水膨胀压力双重作用填塞缝隙,可以有效的防止因接缝不密封出现的渗漏情况,具有较好的密封止水性能,能抗大的水压力。
在舰岛可拆卸部分的设计中,我们采用了轮廓加橡塑胶带的方法,一方面使舱盖固定,另一方面填充缝隙达到防水的效果。
5.4 实现效果在额外载重约700g时,“冲浪者号”吃水过深,并且行进速度大幅降低,全速只有约0.15m/s,而且倾覆角度区间难以满足,于是我们对船体进行了进一步的改进与升级,以达到最初的设计要求。
六、基于定量分析的迭代 6.1 迭代方案思路 基于上述的实验效果并结合Matlab建模仿真的结果进行比照,尽管从船型设计上来讲我们所设计的初代船体外形已经达到了额定的稳性消失角要求,具有一定的扶正能力,但在实际的工程测试过程中我们发现,由于船型设计得过小,在装载上配重后整体的吃水深度较大导致船舶在水中航行的稳定性与扶正力矩相关指标的实际表现并不尽如人意;除此之外,在Matlab仿真过程中给出的除船体外壳外的离散质量点的坐标数据也较为模糊,对于稳性消失角模拟的结果造成了一定程度上的印象。通过以上的分析,我们初步设想在迭代过程中尽可能对船体进行再加工,通过延长船体长度的方式扩大相同吃水深度下排开水的体积以提供更大的浮力,从而控制船体满载情况下的吃水深度仍然在可控范围内;同时在仿真模拟的过程中增加对于电力驱动模块中的电机、电池等具有相当质量的组件的坐标导入与运算,并对于各离散质量点的坐标进行精细化处理使其更接近于实际情况,以提高仿真模拟的准确度与有效性。
6.2 迭代方案的定量分析 6.2.1 船体外形的修正 基于上述的分析结果与初步迭代思路,我们初步定下了延长船体长度的再加工方案,结合对于已有船体的加工现状分析与船体的稳定性考虑,最终决定将船体长度延长至74cm。以下代码给出了对于重新设计的船体的基本参数的定义与设置:
1 2 3 4 5 6 7 8 boat.L = 74 ; boat.W = 16.5 ; boat.HB = boat.W / 2 ; boat.D = 7 ; density_water = 1 ; boat.mass = 653.8 ;
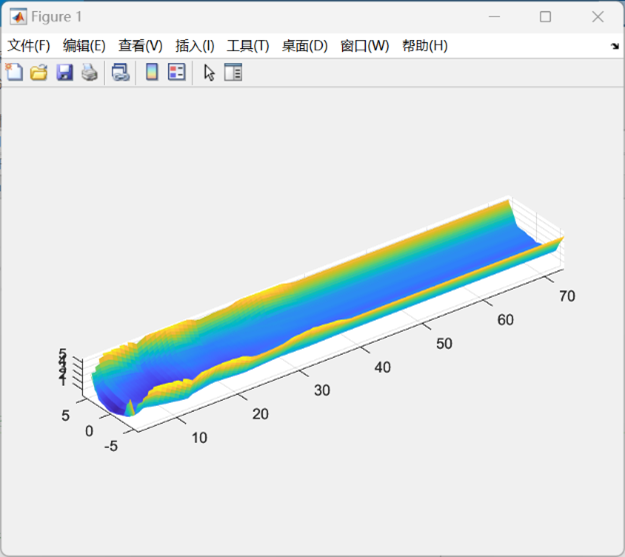
除了船体的宏观参数调整之外,相应的,我们还需要在原有的点集数据基础之上对于延长后的部分进行数据的补充,并将新的点云数据集存储在Matlab文件中,再利用cftool曲线拟合器工具获得新的拟合函数表达式并导入函数文件calculate.m中以在后续的仿真模拟中重复调用。下图展示了新点云数据集所拟合出的函数曲面图像以及对应拟合函数的表达式:
在仿真验证的程序中,我们在导入新的点云数据后,为了进一步验证数学模型建构的准确性,仍然需要通过插值函数griddata补充数据并绘制函数曲面图像与fusion 360建模结果进行一定的比对,效果图如下:
6.2.2 离散数量点数据的校准与补充 在第一代船的仿真模拟数据中,我们在船体外壳的点云数据之外仅补充了配重与桅杆两部分的质心坐标数据及其质量,而忽略了电控模块其余组件的相关数据,且显然由于电控模块中电池与电机的重量相对于船体整体重量来说并不可忽略不计,所以在本次迭代过程中,在Matlab仿真程序的代码实现中对于这一部分进行了补充,同时对于船体中各零散组件的质心坐标及其质量进行了相对精准的测量与估算,从而提高仿真模拟的准确度,使其更加贴近实际情况。补充调整后船体内的离散质量点的相关数据如下列程序段所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 m1=356 ; boat.finalmass=boat.mass+m1; x1=34 ; y1=0 ; z1=9.8 ; m2=356 ; boat.finalmass=boat.finalmass+m2; x2=44 ; y2=0 ; z2=9.5 ; m3=116 ; boat.finalmass=boat.finalmass+m3; x3=39 ; y3=0 ; z3=49.5 ; m4=116.1 ; boat.finalmass=boat.finalmass+m4; x4=0 ; y4=39 ; z4=12.5 ; m5=49.4 ; boat.finalmass=boat.finalmass+m5; x5=64.5 ; y5=0 ; z5=6.2 ; m6=185.1 ; boat.finalmass=boat.finalmass+m6; x6=12 ; y6=0 ; z6=5.5 ; m7=190.4 ; boat.finalmass=boat.finalmass+m7; x7=53 ; y7=4 ; z7=3 ; m8=191.6 ; boat.finalmass=boat.finalmass+m8; x8=53 ; y8=-4 ; z8=3 ; m9=49.4 ; boat.finalmass=boat.finalmass+m9; x9=20.5 ; y9=6 ; z9=7 ; m10=49.6 ; boat.finalmass=boat.finalmass+m10; x10=20.5 ; y10=-6 ; z10=7 ; m11=43.5 ; boat.finalmass=boat.finalmass+m11; x11=73.5 ; y11=3.8 ; z11=1 ; m12=40.3 ; boat.finalmass=boat.finalmass+m12; x12=73.5 ; y12=-3.8 ; z12=1 ; m13=18.2 ; boat.finalmass=boat.finalmass+m13; x13=20.5 ; y13=0 ; z13=6.3 ; density=boat.mass/tnt; COM_x=(COM_x*density+m1*x1+m2*x2+m3*x3+m4*x4+m5*x5+m6*x6+m7*x7+m8*x8+m9*x9+m10*x10+m11*x11+m12*x12+m13*x13)/boat.finalmass; COM_y=(COM_y*density+m1*y1+m2*y2+m3*y3+m4*y4+m5*y5+m6*y6+m7*y7+m8*y8+m9*y9+m10*y10+m11*y11+m12*y12+m13*y13)/boat.finalmass; COM_z=(COM_z*density+m1*z1+m2*z2+m3*z3+m4*z4+m5*z5+m6*z6+m7*z7+m8*z8+m9*z9+m10*z10+m11*z11+m12*z12+m13*z13)/boat.finalmass;
在获得了更加精准的离散质量点的相关数据后,我们可以利用上述程序段的最后部分来计算整个船体在装载了配重与电力驱动模块后的重心在x、y、z轴上的坐标,结果如下图所示:
6.2.3 稳性消失角的最终呈现 经过上述结合实际情况后对于点云与离散质量点的数据补充与完善,我们将新的数据导入Matlab程序并再次运行,最终得到了如下图所示的l-θ图像以反映船体倾斜角度与扶正力臂之间的函数关系:
该图也成功体现了改进后的船型设计仍然能够使得稳性消失角维持在120-140度之间,能够满足对于船体稳定性与扶正能力的相关要求,可以进行下一步的迭代加工操作。
七、迭代产品制造过程与实现效果 7.1 迭代产品制造 7.1.1 船体再制造为解决原有船体载重后吃水过深的问题,第二代的“刃海级”加长了“冲浪者号”船体长度,本次船体长度在制造前进行了较为周密的运算(各模块重量数据见程序部分),通过对各模块质量的初步掌握,以及配重块和所载重物的估计重量,结合原船型截面面积,计算出额在不改变原有船模外形的前提下,所需加长船身的长度以及大致的吃水情况(船体加长至74cm,空载预估吃水2.87cm,满载预估吃水4.56cm,后经实验实际情况与估计值差距不超过10%)
7.1.2 电控系统改进由于船体整体加大增重以及为解决之前动力不足的问题,更换了另外一套控制系统(功率更大的电机,螺旋桨,电池,电子调速器以及信号接收发遥控系统),改进后的推力更强,满足了设计要求中对动力的需求。
电机参数情况:
实际安装情况:
7.1.3 驱动优化以及节能设计在更换大功率电机之后,电机发热明显增加,为了提高船舶的安全性,可靠性,在迭代过程中,加入了水冷却系统。除此之外为了合理利用船体空间并节约一定能源,在船舶顶部加装了与冷却系统相连的供电装置。
太阳能板与内置电池串联,同时并联水泵与控制板,达到水冷与控制喷水的效果。
额定发电电压:6V
发电最大:150mA
尺寸:60mm*110mm
7.2 迭代产品实现效果 7.2.1 实验效果
空载条件下,倾覆角150°
载有饮料的条件下倾覆角大约为130°
7.2.2 微调满足设计要求船舶下水后未调整前倾覆角明显大于140°,于是在船体舰岛舱内加装配重块(仓顶左右两侧各25g),空载倾覆角135°左右,满载倾覆角125°左右。
八、最终成品与总结 8.1 “刃海级”
8.2 项目总结与感悟本次项目历经两次迭代,最后基本实现了项目设计要求,产品还存在需要改进的地方。第一代“冲浪者号”设计中在定量化设计步骤中有疏忽掉配重块的问题,帮助我们发现了我们定量化设计方法的问题所在,总结了第一代的经验之后第二代“刃海级”较为成功地实现了项目设计地要求。
产品的研发设计离不开严格的定量化分析,更离不开多次地迭代更新,在这个过程中我们可以不断学习用到的相关知识,包括电路,控制,材料,结构,力学,软件等等一系列的相关知识,给了我们更开阔的眼界,也锻炼了我们的能力和意志。最重要的是教会了我们定量化分析的思想,为以后项目及产品的开发提供了极大的帮助!





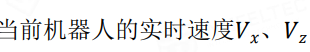
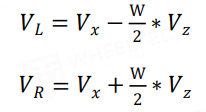
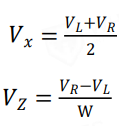



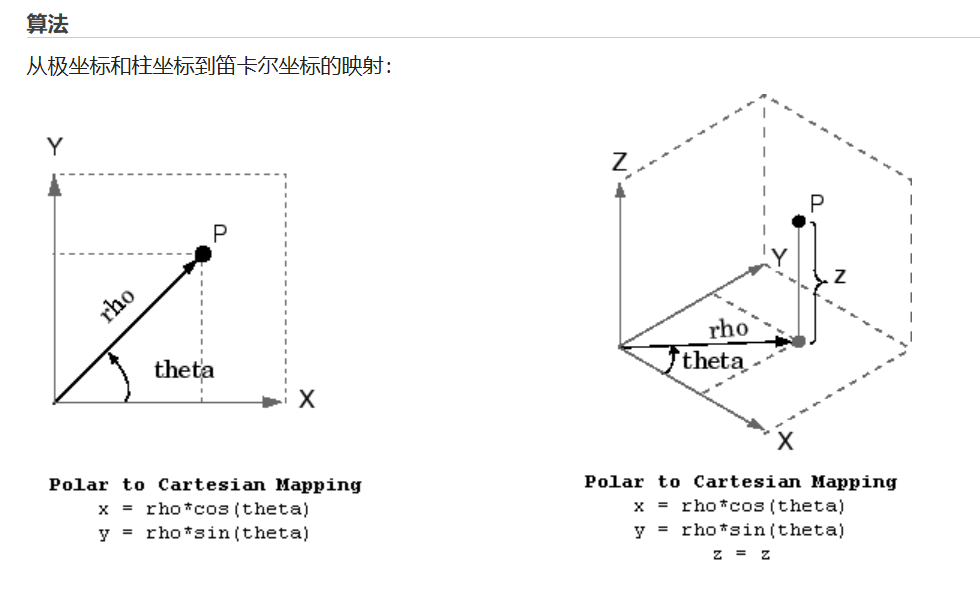
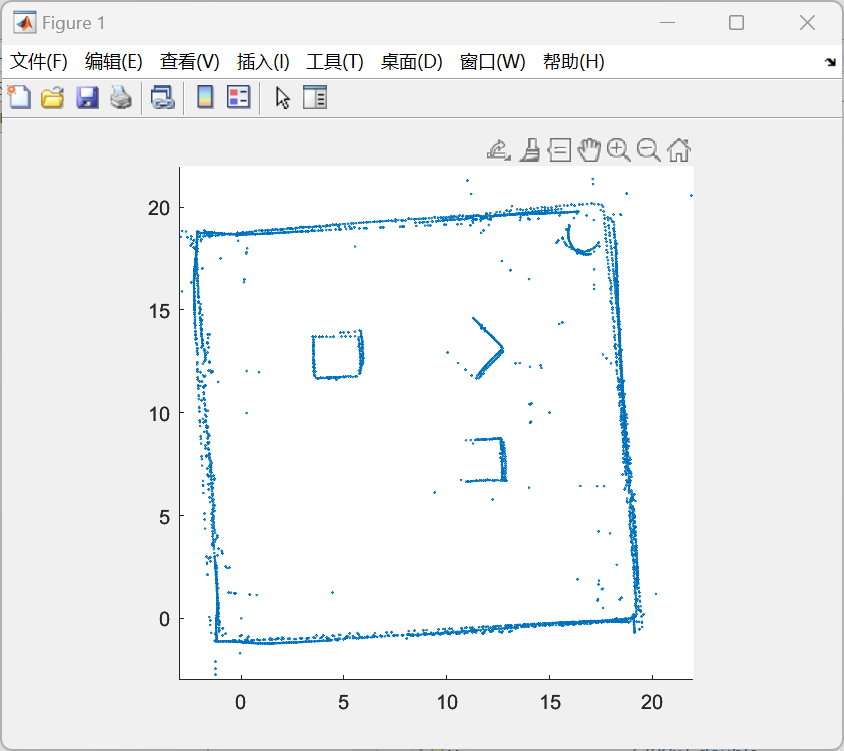
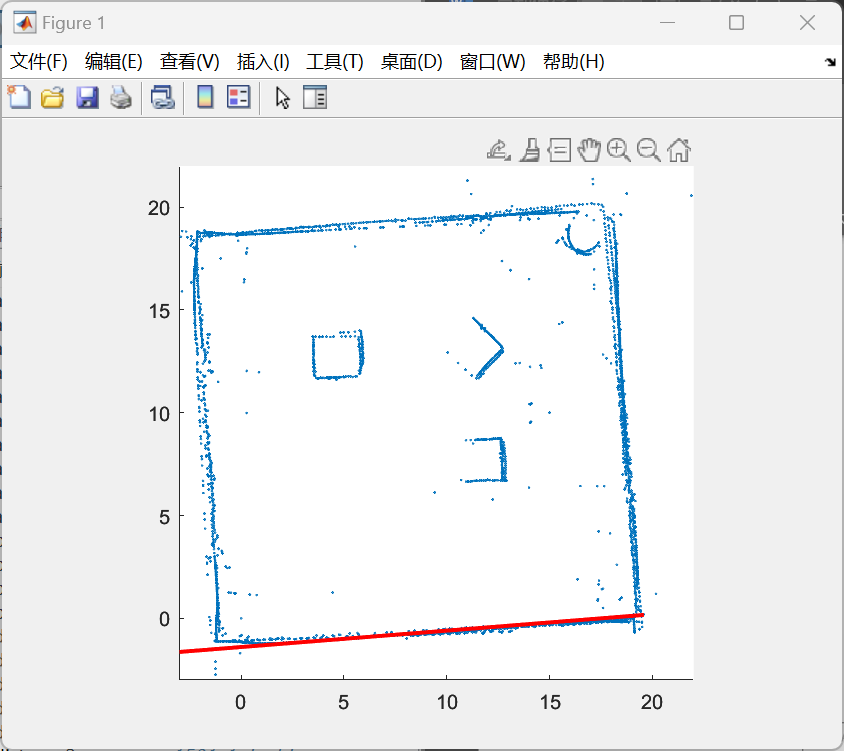
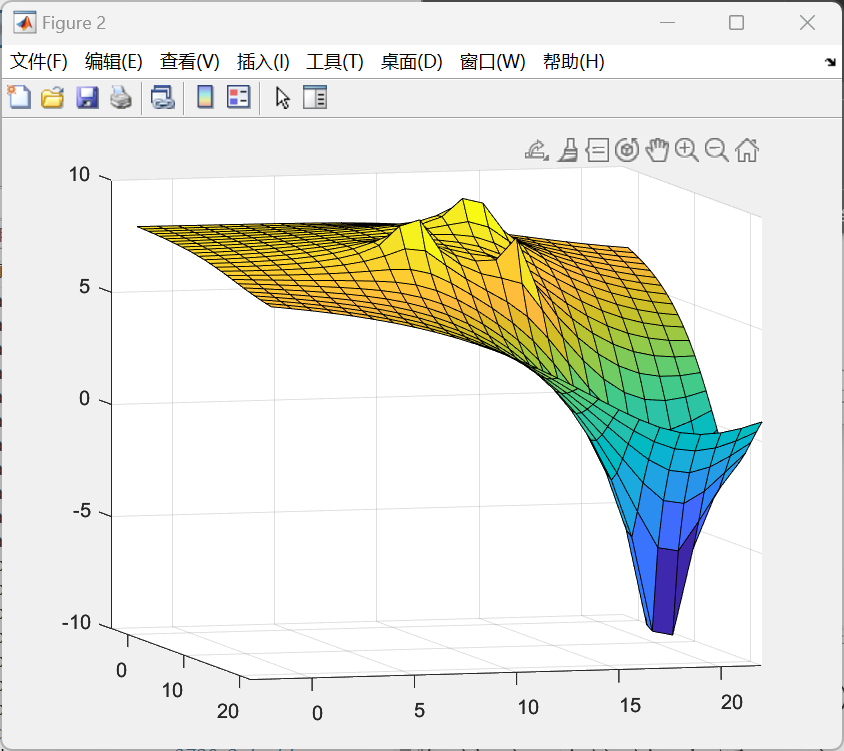
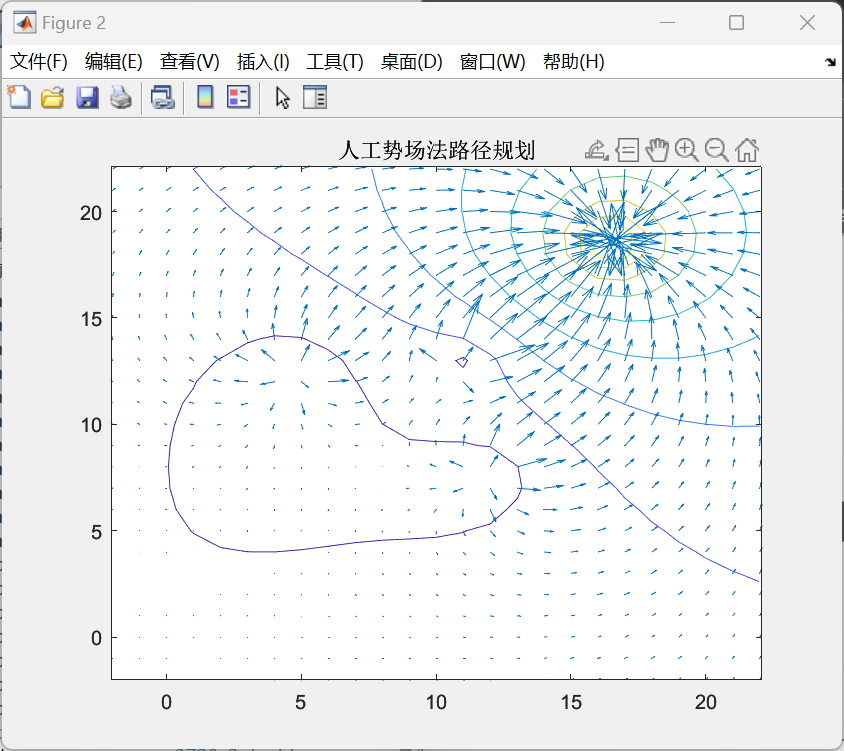
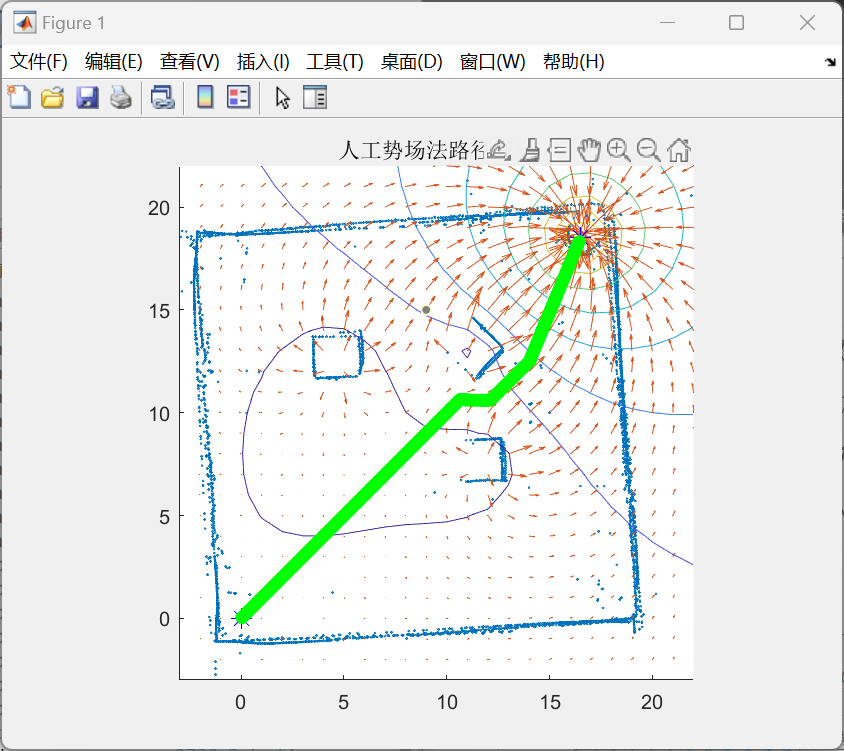
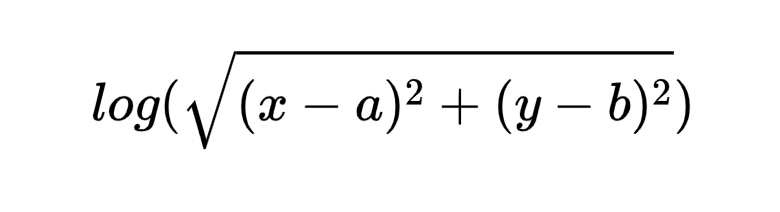 (a,b即为障碍物/目标点的x,y坐标)建立势场。通过观察不难发现,在以(a,b)为圆心、半径为1的圆之外的地方该势函数均为正,反之为负。事实上,对于场地内的3个障碍物以及1个目标物而言,所形成的是一个叠加场,由原型函数作用于不同的点叠加而成。在此,我们不妨认为势场为正处具有排斥力而势场为负处具有吸引力,需要吸引小车向目标点走去而花费尽量少的能量。在这样的算法理念基础上,我们需要在代表目标点的原型函数部分加上负号;更进一步的,我们还希望这个吸引力足够大而防止被障碍物阻断,因此在建立势场时,不妨在代表目标点的原型函数前乘上一定的系数以保证其足够强大的吸引力。最终,我们根据地图实际情况,建立了整个势场叠加后的函数方程:F=log(sqrt((x-4.75).^2+(y-12.5).^2))+log(sqrt((x-12).^2+(y-7.6).^2))+log(sqrt((x-11.2).^2+(y-13).^2))-5*log(sqrt((x-16.5).^2+(y-18.5).^2)),并根据该函数绘制了势能图(如图4-5)与等势线图(如图4-6)。
(a,b即为障碍物/目标点的x,y坐标)建立势场。通过观察不难发现,在以(a,b)为圆心、半径为1的圆之外的地方该势函数均为正,反之为负。事实上,对于场地内的3个障碍物以及1个目标物而言,所形成的是一个叠加场,由原型函数作用于不同的点叠加而成。在此,我们不妨认为势场为正处具有排斥力而势场为负处具有吸引力,需要吸引小车向目标点走去而花费尽量少的能量。在这样的算法理念基础上,我们需要在代表目标点的原型函数部分加上负号;更进一步的,我们还希望这个吸引力足够大而防止被障碍物阻断,因此在建立势场时,不妨在代表目标点的原型函数前乘上一定的系数以保证其足够强大的吸引力。最终,我们根据地图实际情况,建立了整个势场叠加后的函数方程:F=log(sqrt((x-4.75).^2+(y-12.5).^2))+log(sqrt((x-12).^2+(y-7.6).^2))+log(sqrt((x-11.2).^2+(y-13).^2))-5*log(sqrt((x-16.5).^2+(y-18.5).^2)),并根据该函数绘制了势能图(如图4-5)与等势线图(如图4-6)。