1 项目背景与研究意义
1.1 项目背景
肺炎作为一种常见的呼吸系统疾病,对人类健康构成了长期威胁,特别是随着COVID-19新冠肺炎疫情的全球爆发,其公共健康影响更为显著。COVID-19肺炎具有传播速度快、感染范围广、诊断难度大的特点,对全球医疗系统和社会经济产生了深远影响。特别是在疫情高峰期,医疗资源的短缺和诊断效率的瓶颈,进一步突显了快速、准确诊断工具的重要性。
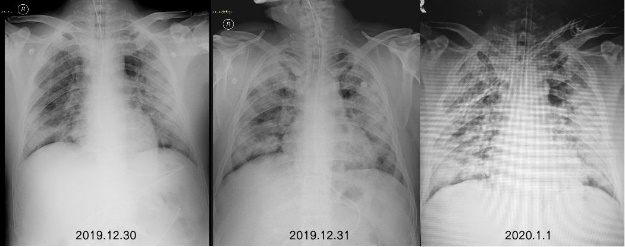
传统肺炎诊断方法主要依赖医生对胸部X光片或CT图像的人工分析,既耗时又容易受到经验和疲劳的影响,尤其在COVID-19疫情期间,大量影像数据的涌现使得人工诊断难以满足需求。与此同时,COVID-19的影像表现与其他类型肺炎的重叠性增加了诊断的复杂性,这进一步加剧了对智能化诊断系统的需求。
随着人工智能技术的快速发展,深度学习为医疗影像分析带来了全新的解决方案。卷积神经网络(Convolutional Neural Network, CNN)凭借其强大的图像特征提取能力,在自动化诊断中展现了巨大潜力。同时,由于不同医疗机构的CT扫描设备性能差异显著,特别是在医疗资源较为匮乏的地区,CT影像常常受到设备老化、分辨率低或操作不规范等因素的影响,图像质量参差不齐,这不仅增加了诊断的复杂性,还对自动化系统的鲁棒性提出了更高要求;而自编码器(Autoencoder)作为一种有效的降噪工具,为医疗影像数据预处理提供了重要支持。通过自编码器的引入,可以有效消除图像中的噪声干扰,减少不同设备间的成像差异,为后续的分类和识别模型提供高质量的输入数据。因此,本项目提出结合自编码器和卷积神经网络的深度学习框架,开发一套针对肺炎(包括COVID-19)CT影像识别的智能诊断系统。
1.2 研究意义
本项目以新型冠状病毒肺炎为切入点,面向未来医学智能化需求,开发的诊断系统不仅能够应对当下疫情挑战,还具有推广至其他医学影像诊断场景的潜力,从而为全球公共健康事业的发展提供有力支持。
面向新冠肺炎疫情期间大规模肺部影像数据的快速诊断需求,本系统依托深度学习技术,有效提升了诊断效率,为疫情防控和患者管理提供重要的技术支持。通过先进的模型算法,系统能够精准识别肺部CT影像中的病变特征,减少人为误差,确保诊断结果的准确性和一致性,大幅降低不同医疗机构和医生之间的诊断差异,避免误诊和漏诊风险,从而更好地保障患者安全。
针对基层医院或偏远地区医疗资源匮乏的现状,本系统可作为一种可靠的辅助诊断工具,为医生提供科学的决策支持,帮助缓解诊断能力不足带来的压力。其高效的处理能力不仅提高了基层医疗服务水平,也为疫情防控的全面推进提供了技术保障,为应对紧急医疗需求的地区解决实际困难。
此外,本系统在高效处理和分析海量肺部CT影像数据的基础上,还为研究新冠肺炎的病理特征及流行规律提供了宝贵的数据支持。这些分析结果可进一步应用于疫情传播趋势预测和公共卫生政策制定,为疫情防控策略的科学性和有效性奠定了坚实基础。
同时,本系统也为患者病情的动态管理提供了重要帮助。通过智能分析新冠肺炎影像特征的变化趋势,系统能够为临床医生提供精确的病情评估建议,有助于及时调整治疗方案。这种基于影像数据的技术支持,不仅提高了患者管理的科学性和有效性,还为医疗资源的合理分配提供了重要依据,进一步推动了疫情防控工作的高效开展。
2 数据集获取与预处理
2.1 数据集介绍
本项目使用的肺部X-光片数据集从Kaggle网站(链接:https://www.kaggle.com/datasets/alsaniipe/chest-x-ray-image)获取,共分为三类标签:新冠肺炎COVID19、正常NORMAL和普通肺炎PNEUMONIA,该数据集已经事先划分好了训练集与测试集。此外,为测试模型对于不同质量CT影像的识别精度,还对测试集中的部分图像使用高斯噪声进行扰动,以模拟实际CT扫描的成像质量差异。
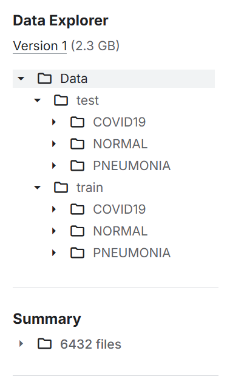
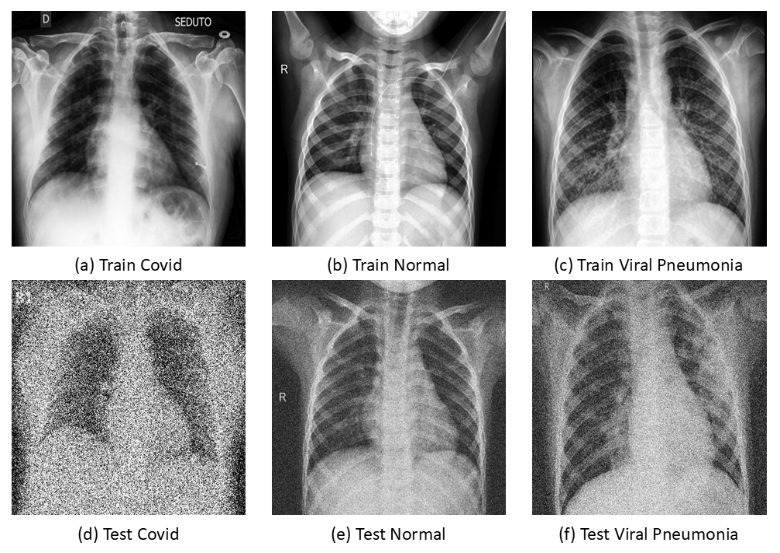
数据分布如下表所示:
表2.1:数据集数据分布情况
| COVID19 | NORMAL | PNEUMONIA | |
|---|---|---|---|
| Train | 460 | 1266 | 3418 |
| Test | 116 | 317 | 855 |
| Noisy_Test | 26 | 20 | 20 |
2.2 编程环境搭建
本项目中所有的代码编写与运行均是在配备NVIDIA GeForce RTX 3060显卡、16GB运行内存、12th Gen Inter(R) Core(TM) i7-12700@2.10GHz处理器与Microsoft Windows 11操作系统的工作站上使用Python编程语言完成的。
软件环境方面,采用Conda进行环境管理,在控制台中通过命令”conda create -n covid python=3.12”创建虚拟环境,并在激活环境后使用pip install命令依次安装所需的各种依赖库;全部安装并测试完成后,通过命令”pip freeze >
requirements.txt”将虚拟环境中安装的所有依赖库及对应版本写入文件requirements.txt,后续移植时可在新的运行环境中运行命令”pip install -r requirements.txt”完成环境的一键配置。
值得注意的是,在PyTorch(包括torch、torchvision与torchaudio库)安装时需要根据自己电脑使用的CUDA版本(使用CPU则直接在命令行中使用pip install安装即可)在PyTorch官网中找到对应的安装命令进行安装。我使用的CUDA版本为12.6,安装命令的选取如下图所示:
下面对于项目中使用到的主要依赖库进行简要介绍:
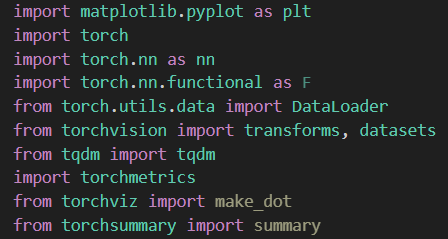
其中,plt用于绘图,nn中包含了用于构建神经网络的隐藏层(全连接层、卷积层等),F中包含了各种激活函数(ReLu、Sigmoid等),DataLoader用于在训练时加载数据,datasets和transforms用于读取和处理数据集,tqdm用于进度条可视化,torchmetrics用于模型精度的测试,torchviz和torchsummary用于以图形与文字的方式描述模型架构概况。
2.3 图像数据读取
torch对于一些常用的数据集做了封装,可以直接调用,例如datasets.MNIST()。但此处我们使用的是本地的图片数据,可以使用ImageFolder将一个文件夹下的图片读取成数据集并完成数据增强工作。在读取完数据集后,还需要定义DataLoader用于加载数据为可分批次(batch)读取的迭代器以供后续使用。为使得代码更加简洁,将上述的数据读取与加载过程为封装在getDataLoader函数中,并在主函数中通过指定不同的目录加载训练集、测试集或是含噪声测试集。
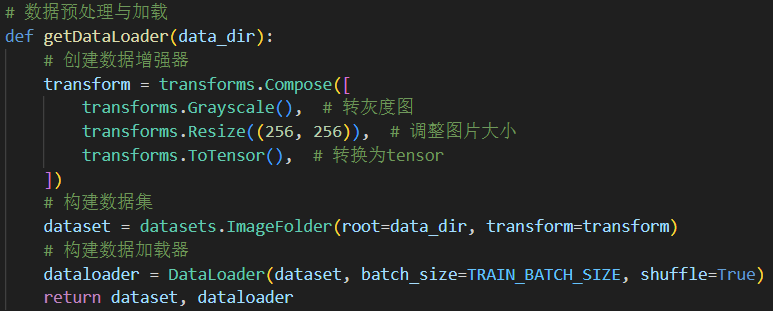
可以看到,其中构建了数据增强器transform,在读取数据时进行相应处理:
Grayscale: 指以灰度图的形式读取。
Resize: 由于图像尺寸各不相同,在训练前需将它们重塑成相同尺寸256*256。
ToTensor: 将图片格式转换成张量形式,torch的计算以张量的形式进行。
除此之外,在构建数据加载器时需要指定一个批次(batch)中的图片数据数量batch_size,在模型训练时训练批次大小TRAIN_BATCH_SIZE也是会影响最终模型性能的重要超参数之一。在训练过程中,设定TRAIN_BATCH_SIZE为32,而在测试过程中,为提高测试效率,将TEST_BATCH_SIZE设置为66并对函数进行对应修改。
2.4 叠加噪声函数
不论是构建噪声测试集,还是在利用无噪声的训练集进行训练时,都需要手动添加噪声,故编写add_noise函数,默认的噪声强度为0.5,并在添加噪声后进行归一化以确保图像值位于[0,1]范围内。

3 模型构建与网络训练
3.1 整体模型框架
整体模型框架由两个核心部分组成,分别是用于去噪的数据预处理模块和负责分类的卷积神经网络(CNN)。去噪模块采用自编码器(Autoencoder)的架构,专注于从输入数据中去除噪声,以提升后续分类的准确性;分类模块基于卷积神经网络,其强大的特征提取和模式识别能力使其成为分类任务的理想选择。
两个模块相辅相成,通过有效的数据处理和特征提取,确保模型能够在噪声干扰较大的环境中实现高精度分类。噪声数据首先经过自编码器处理,生成质量优化的特征表示,然后被CNN接收并完成分类任务。这一整体框架设计非常适合肺炎图像识别任务,通过结合去噪和分类两大模块的优势,模型不仅能够有效提高数据质量,还能充分挖掘数据中的有用特征,从而能够在复杂的医学影像处理中表现出卓越的鲁棒性和准确性,满足肺炎诊断的实际需求。
3.2 自编码器
自编码器模型用于处理输入数据中的噪声问题,提升后续分类的准确性。其核心思想是通过编码器将输入数据压缩至低维潜在表示(latent representation),再由解码器将其还原至去噪后的重构数据,从而实现降噪效果。
3.2.1 网络结构设计
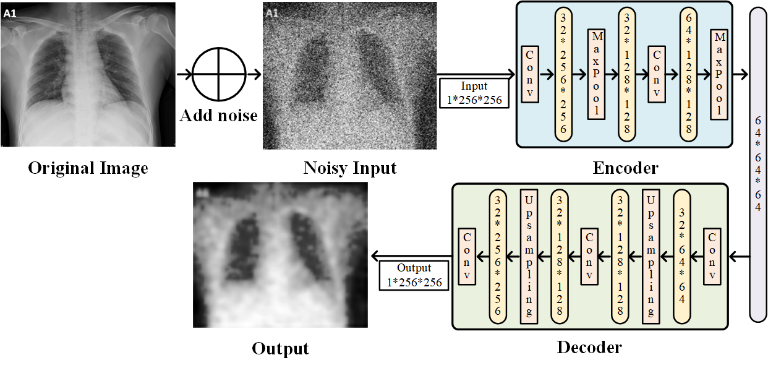
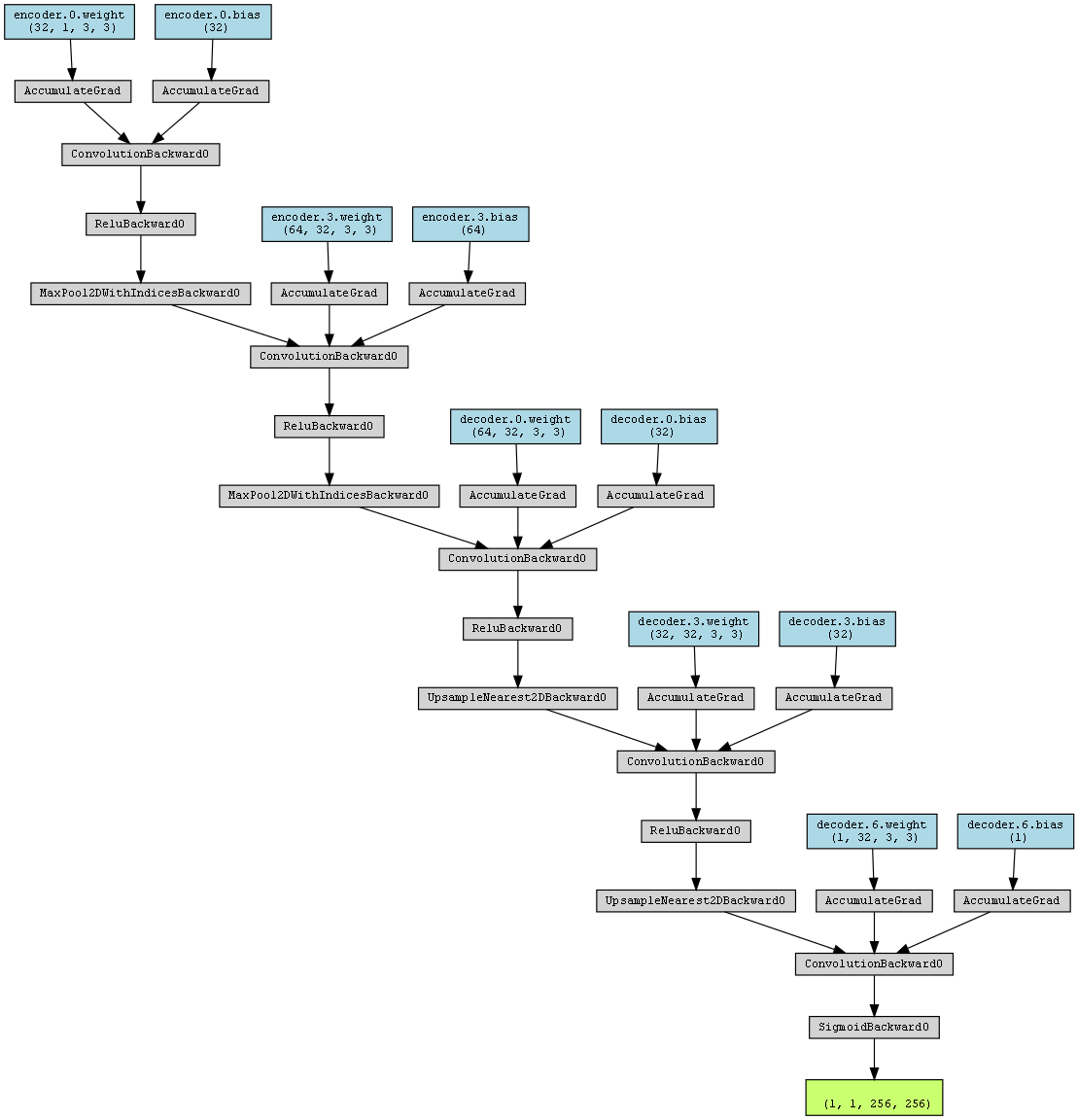
自编码器网络结构由编码器encoder与解码器decoder组成:
编码器由两层卷积(Conv2d)和两次池化(MaxPool2d)操作组成,用于提取特征;
解码器通过两次反卷积(ConvTranspose2d)和两次上采样(UpsamplingNearest2d)逐步恢复图像尺寸到原始大小;
最后使用Sigmoid激活函数将输出值限制在[0,1]区间。
模型定义代码如下:
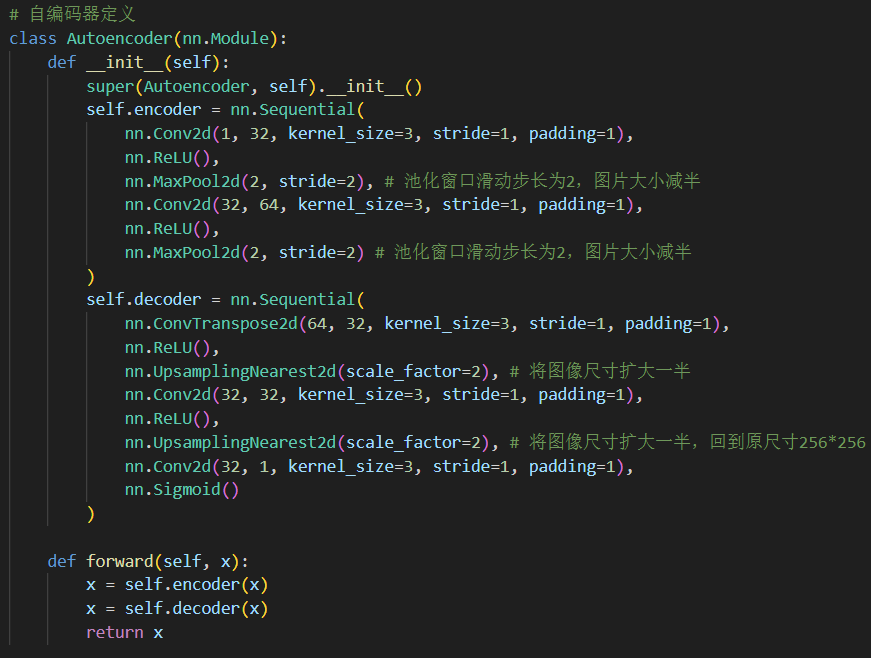
模型继承自nn.Module类,在__init__()函数中定义模型的结构,在forward()函数中定义模型的前向传播过程。
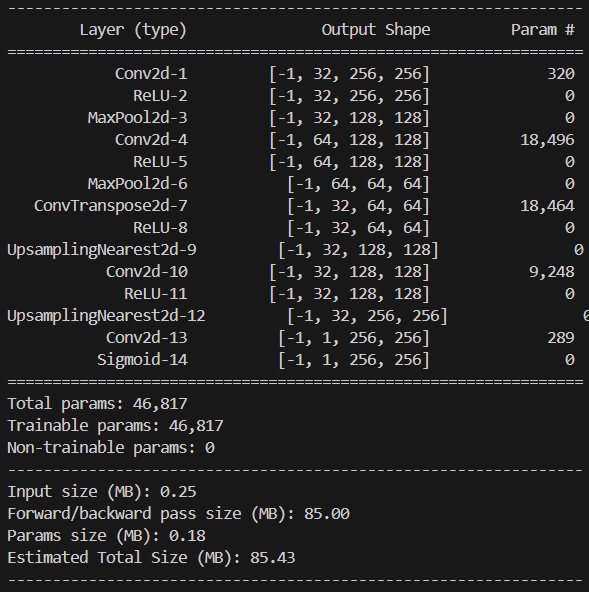
通过调用torchviz和torchsummary库,可以输出该模型结构的基本信息:
3.2.2 模型训练
基本的训练流程集成在函数train_autoencoder_process中,如下图所示:
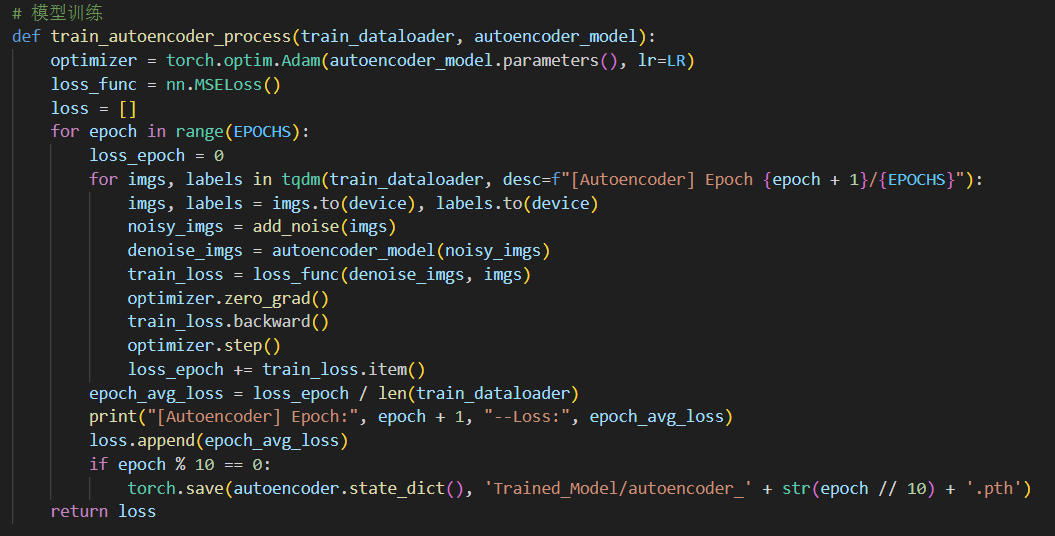
其中指定优化器optimizer为Adam,损失函数为均方误差MSE,并使用超参数:训练轮数Epochs=50、学习率lr=0.001。每轮(Epoch)训练中均需要以多个batch的形式遍历训练集中的所有数据,并在每个batch后对模型进行更新,具体而言每次更新均需执行如下操作:
从加载器中获取输入数据
使用add_noise函数对干净图像加噪
将加噪后图像输入自编码器模型并计算模型输出
根据模型输出和标签计算损失Loss
清空梯度
反向传播
更新模型
值得注意的是,由于用于训练的图像数据没有噪声,因此训练时首先需要对输入的图像进行加噪处理,再输入自编码器模型进行训练。
训练过程中还利用tqdm进度条函数对训练进程进行可视化,并在每轮训练完成后打印出当轮训练过程中模型的平均损失:

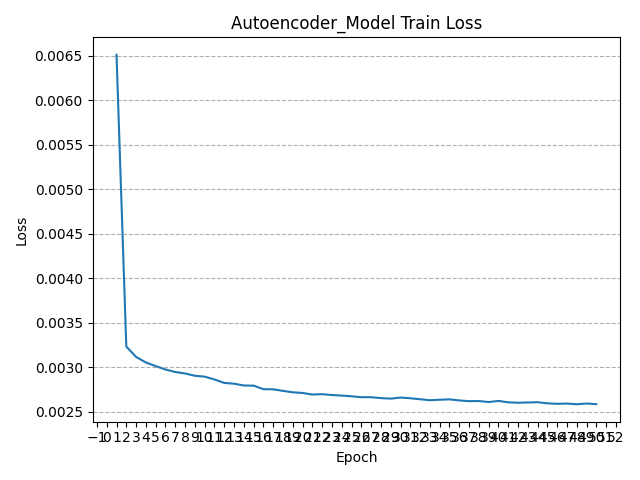
在训练过程中,将每轮训练的平均损失存储在列表中,并在训练结束后将平均损失的变化过程以图像形式呈现:
可以看到,经过多轮训练,模型的损失函数值在不断减小且逐渐趋近于0,这意味着该自编码器的模型训练过程是收敛的,模型具有较稳定的工作性能。
3.3 卷积神经网络
卷积神经网络负责从图像中提取多层次的空间特征,通过逐步减少图像尺寸和增加特征通道来捕捉关键信息,从而实现去噪后肺部CT图像的分类功能。CNN以其强大的特征提取能力,能够有效处理图像的局部依赖性和空间不变性,高效处理结构化数据(如图像、时序数据)。模型简单且高效,具有较强的泛化能力,适合处理小规模数据集的图像分类问题。
3.3.1 网络结构设计
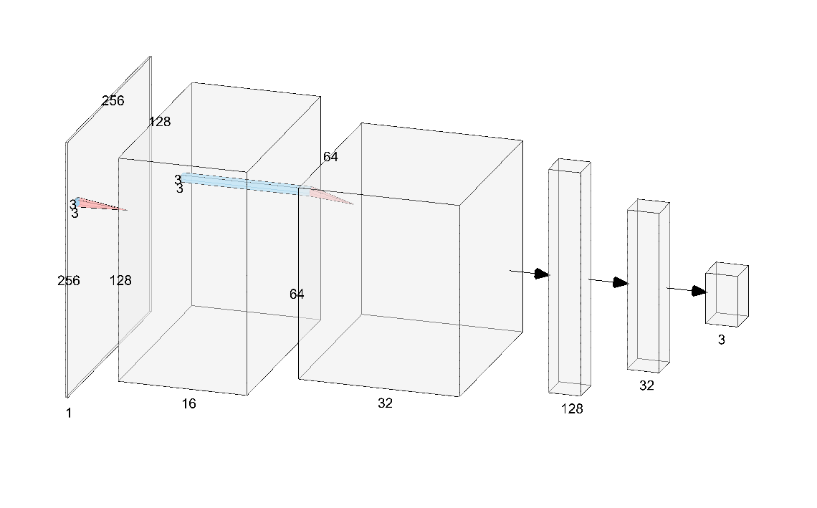
卷积神经网络结构(如上图,通过NN-SVG工具绘制)由两层卷积层(Conv2d)和池化层(MaxPool2d)组成,激活函数均选用ReLU,逐步提取特征并将输入图像的尺寸从原始大小减小到64×64。卷积后的特征图展平后通过三个全连接层(Linear),分别将特征维度从32×64×64降至128,再降至32,最后输出3个类别(Covid19、Normal、Pneumonia)的预测结果。
模型定义代码如下:
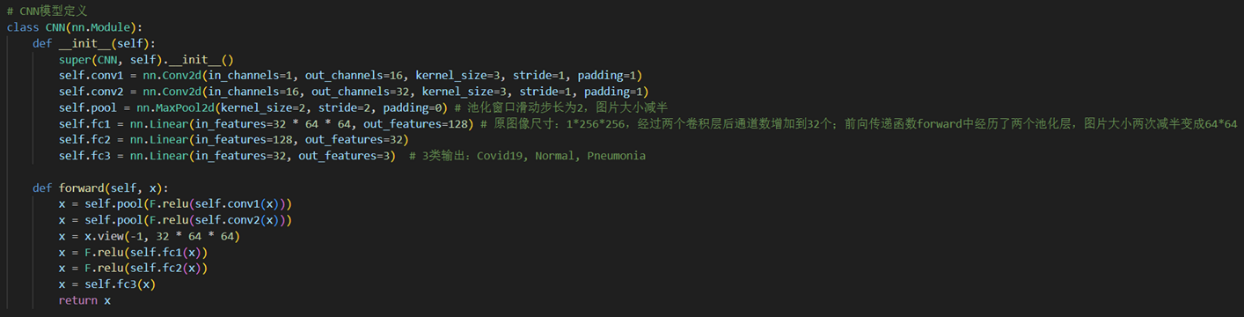
模型继承自nn.Module类,在__init__()函数中定义模型的结构,在forward()函数中定义模型的前向传播过程。
通过调用torchviz和torchsummary库,可以输出该模型结构的基本信息:
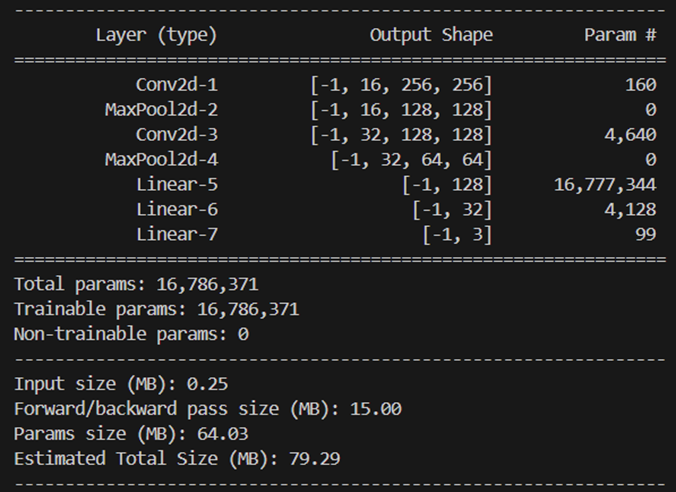
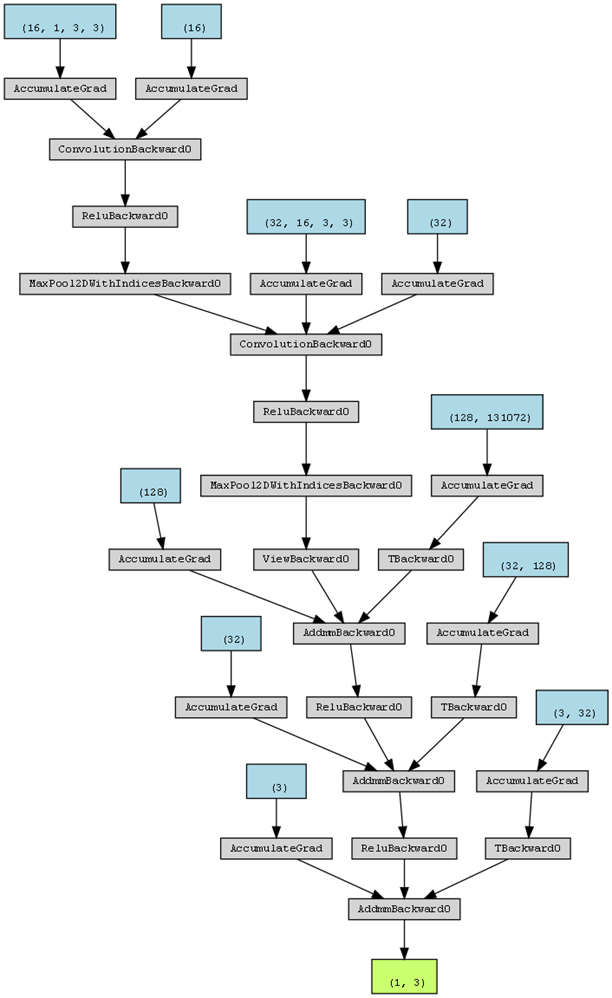
3.3.2 模型训练
基本的训练流程集成在函数train_cnn_process中,如下图所示:
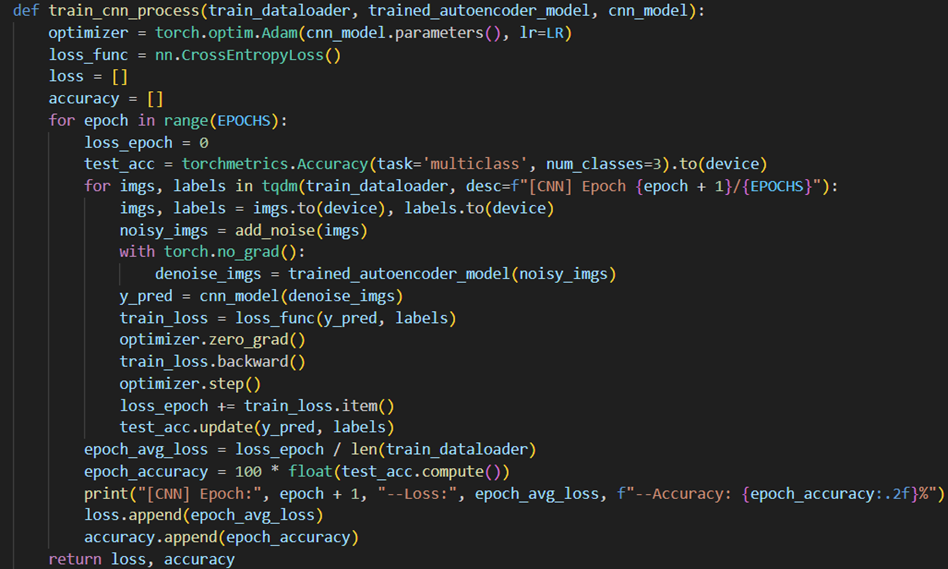
其中指定优化器optimizer为Adam,损失函数为交叉熵损失CrossEntropy,并使用超参数:训练轮数Epochs=50、学习率lr=0.001。每轮(Epoch)训练中均需要以多个batch的形式遍历训练集中的所有数据,并在每个batch后对模型进行更新,具体而言每次更新均需执行如下操作:
从加载器中获取输入数据
使用add_noise函数对干净图像加噪
将加噪后图像输入训练好的自编码器模型trained_autoencoder_model
将经过自编码器去噪后的图像输入CNN模型并计算模型输出
根据模型输出和标签计算损失Loss
清空梯度
反向传播
更新模型
值得注意的是,由于用于训练的图像数据没有噪声,为与实际的输入情况一致,首先需要对输入的图像进行加噪处理,再利用训练好的自编码器模型进行降噪(为了不在更新CNN的同时更新自编码器,这一步不需要产生梯度),才能输入CNN分类模型进行训练。
训练过程中还利用tqdm进度条函数对训练进程进行可视化,并在每轮训练完成后打印出当轮训练过程中模型的平均损失与在训练集上的测试精度:

在训练过程中,将每轮训练的平均损失与模型在训练集上的测试精度存储在列表中,并在训练结束后将两者的变化过程以图像形式呈现:
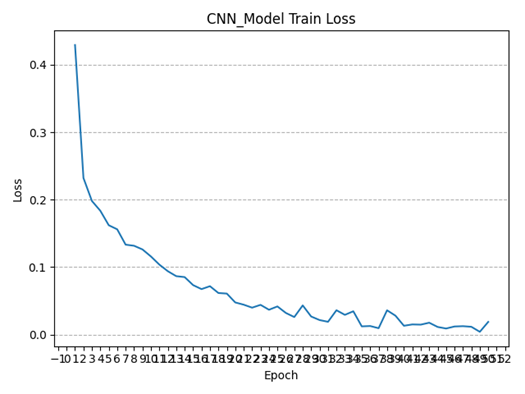
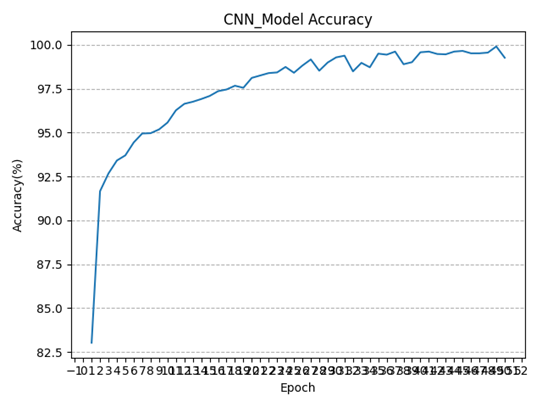
可以看到,经过多轮训练,模型的损失函数值在不断减小且逐渐趋近于0,这意味着该自编码器的模型训练过程是收敛的,模型具有较稳定的工作性能;同时随着训练轮数增加,模型在训练集上的精度也逐渐增高(波动上升),在模型训练完成时,卷积神经网络在训练集上的分类精度已经可以达到99.59%(一度达到99.90%),接近百分之百,说明模型的分类能力较好。
4 模型测试及应用
4.1 自编码器降噪效果
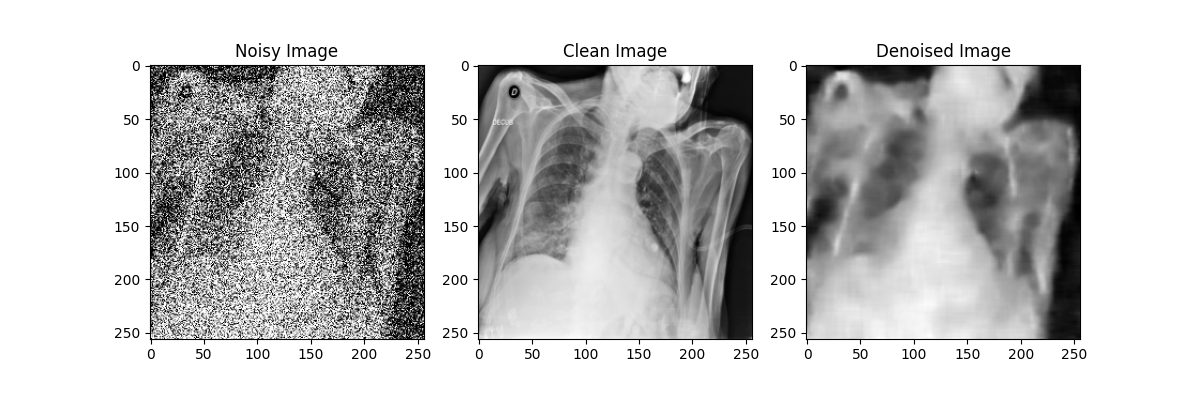
在自编码器模型的训练过程中,每隔10轮对模型参数进行了一次存档;在测试过程中,分别使用训练轮数为10、20、30、40、50的自编码器模型对于加噪后的模型进行降噪处理,效果如下图所示:
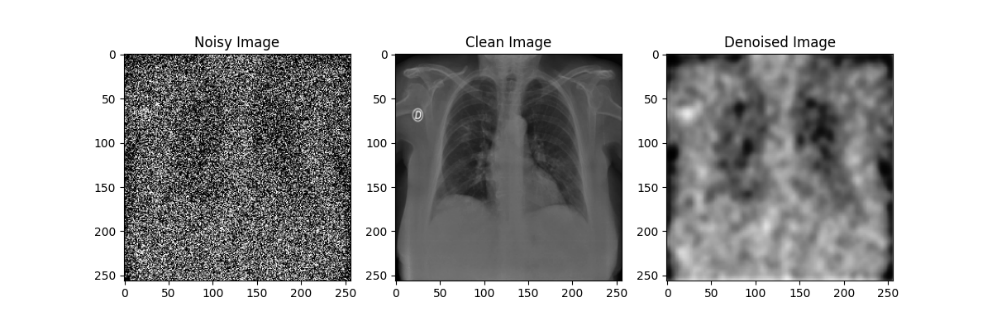
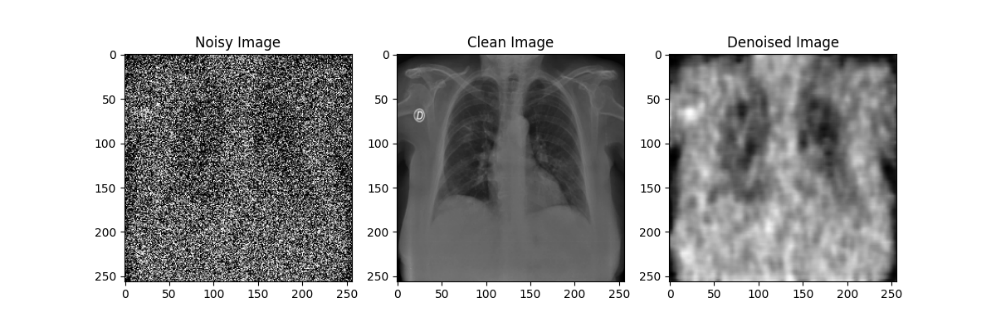
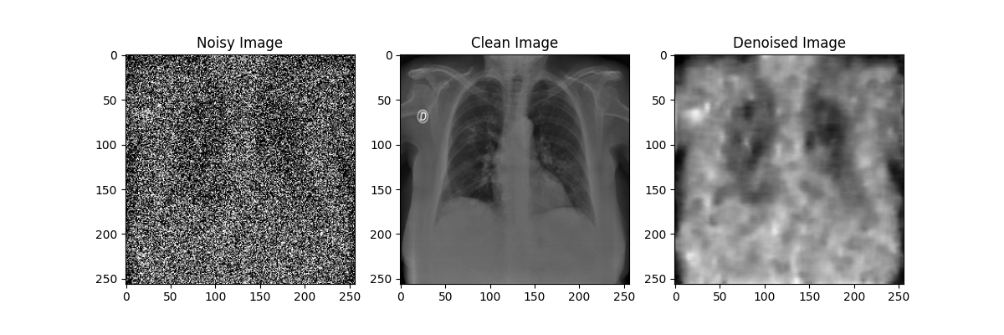
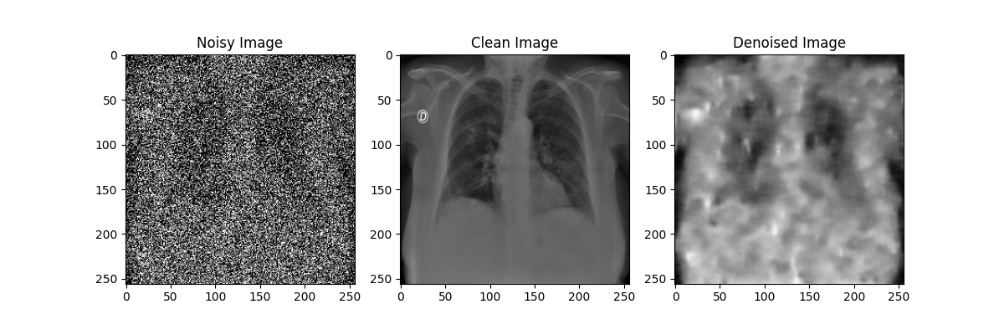
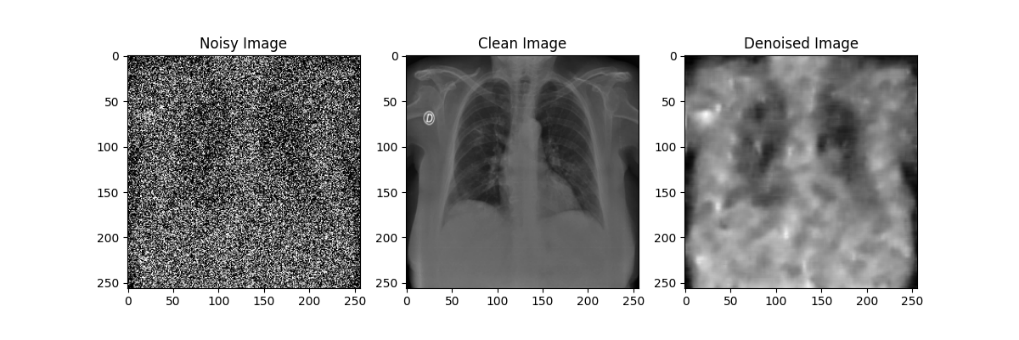
通过对比不同训练轮数的自编码器模型降噪效果可以发现,随着训练轮数的增加,自编码器模型的降噪效果在逐渐提升,但在Epoch到达30之后,训练带来的降噪效果提升就不如先前显著了。尽管由于较大的噪声强度(0.5)导致降噪后的图像仍然比较模糊,但通过肉眼还是能粗略观察处肺部骨骼的轮廓等特征,后续实验也证明了卷积神经网络确实可以从这样清晰度的图像中提取相应的特征来进行分类,该自编码器模型的设计有效。
4.2 卷积神经网络分类精度
在卷积神经网络的分类精度上,训练过程中已经实时对于每一轮训练后的模型在训练集上进行了精度测试(3.2.2节中已有提及),而在测试集上,可以编写与训练过程类似的代码利用torchmetrics库对模型分类精度进行测试,只是不会更新模型,代码如下:
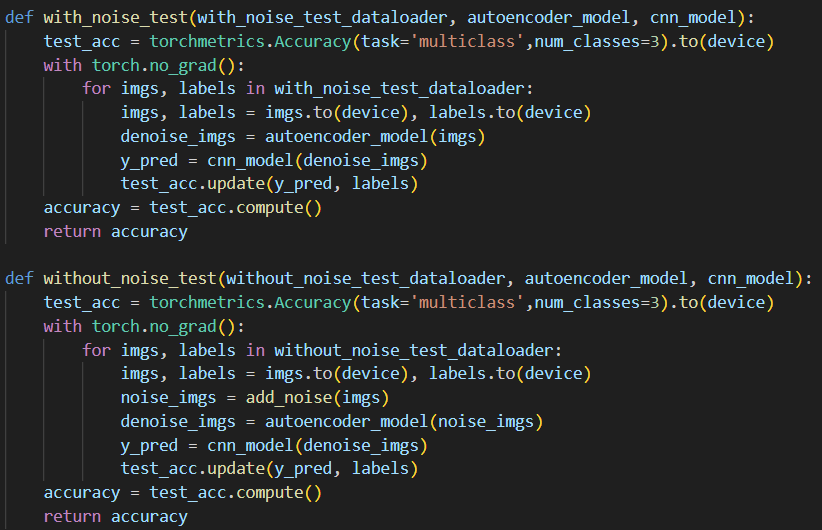
可以看到,由于我们的测试集分为含噪声和不含噪声两类,因此编写了不同的函数对模型分类精度进行测试。两个函数的主要差别就在于,由于含噪声测试集是已经加噪的图片(噪声与手动通过add_noise函数添加的不同),因此在含噪声测试集的测试代码中不必再次手动添加噪声,而是直接将图像输入自编码器降噪后再输入CNN分类模型中进行分类;而对于不含噪声的测试集而言,为模拟与训练集同样的处理流程,会先进行手动加噪再通过自编码器降噪之后才输入CNN分类模型中进行分类。
运行测试代码后,得到模型在含噪测试集上的分类精度为96.97%,在不含噪声的测试集上的分类精度为94.57%,在两个测试集上的分类精度水平均较高,说明该模型具有良好的分类效果。
4.3 模型应用:基于CT影像的肺炎诊断Web服务
通过对比多组超参数的模型降噪与分类效果,最终选定如下的超参数:
训练轮数Epochs=50;
学习率LR=0.001;
训练批次大小Train_Batch_Size=32。
选定参数后,将整体代码抽离为model.py(包含模型定义类代码),run.py(服务端代码)和train.py(训练函数),并将模型部署到实际应用中,使用Flask作为服务端,以Web形式用户提供操作接口以上传图片进行诊断。由于主要功能是提供接口,故网页只做了很简易的一个index.html,给用户提供上传图片的按钮,并在用户上传有噪声的CT影像后返回诊断结果及去噪后的图像。除此之外,还将挂载在本地端口上的Web通过内网穿透映射到公网,以供实时访问。
网页初始界面如下图所示:
接下来分别测试当输入COVID19、NORMAL和PNEUMONIA三个组别的图片,模型能否正确判断:
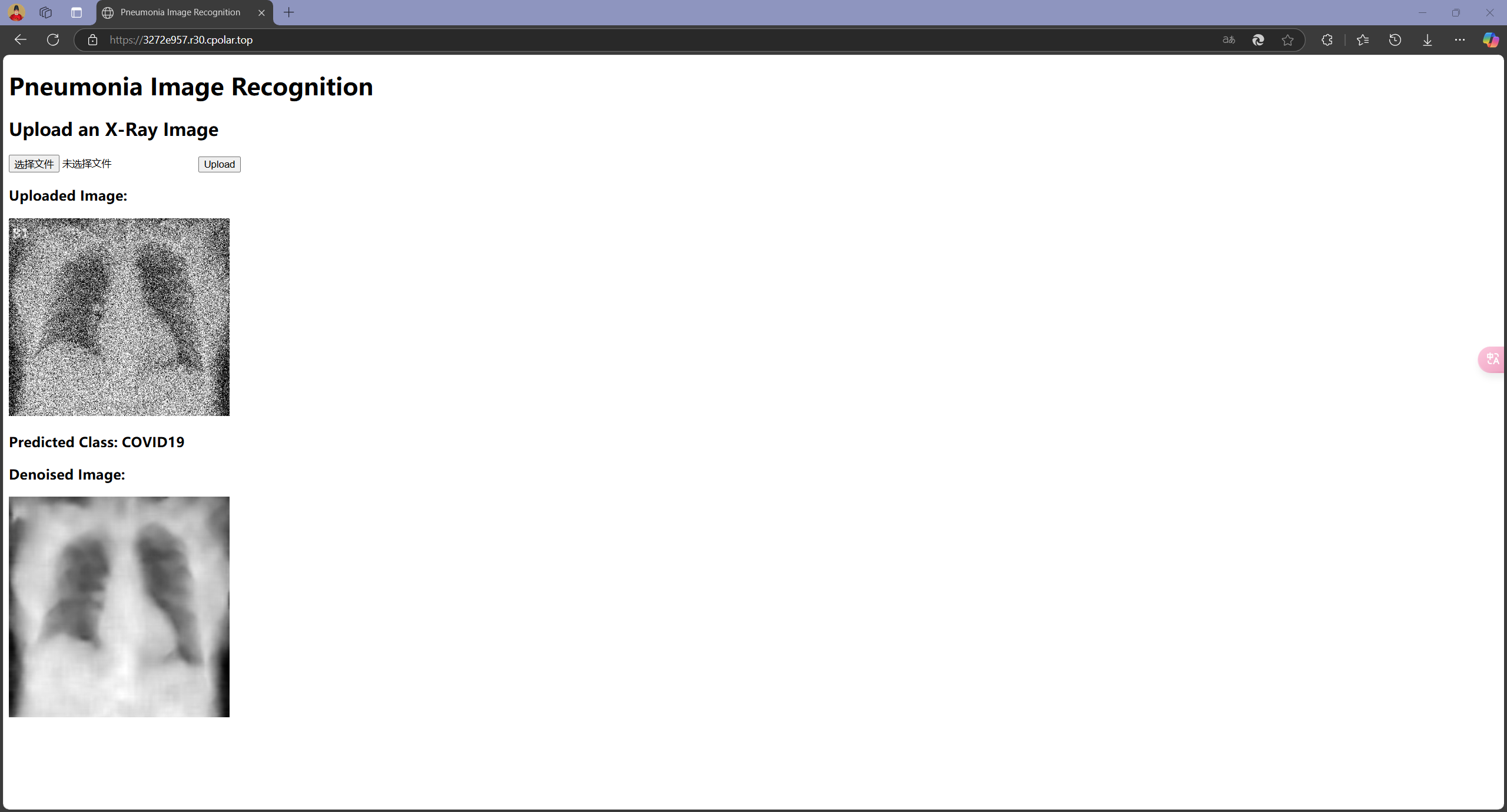
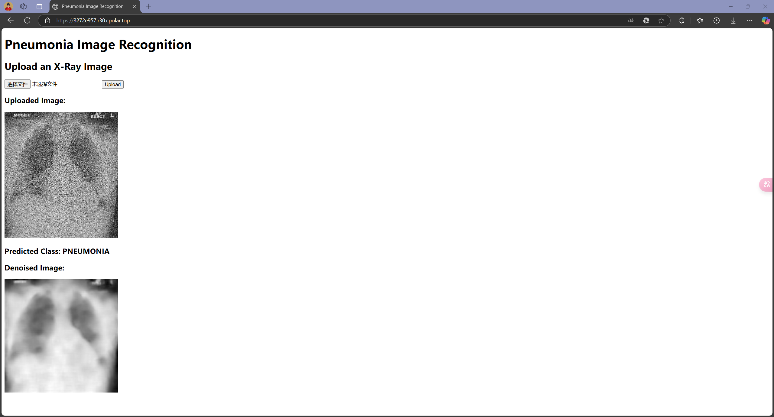
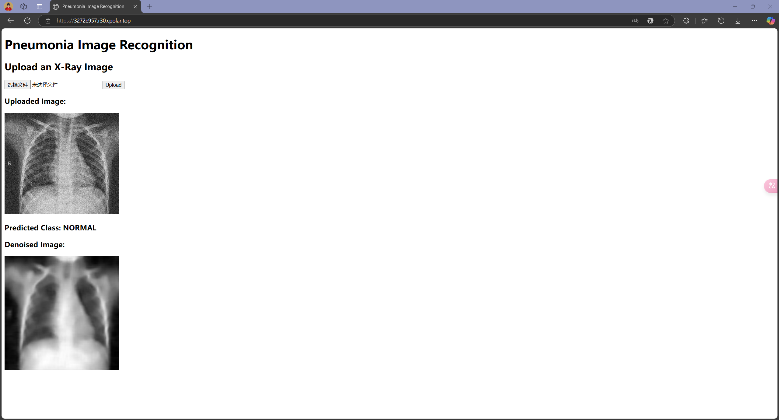
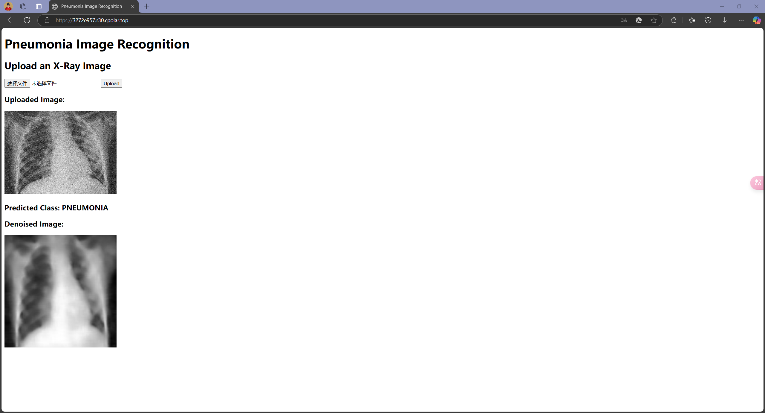
可以发现,模型在大多数情况下可以正确识别图像来源,但也会出现错误识别的情况,这和Test 集上的Accuracy相符合;此外,在测试时还注意到,模型识别结果偶尔会出现不稳定的现象,即输入同一张图像有时识别为某一类别,有时又会识别为另一类别,这是由模型内部部分随机参数导致的,这也反映了模型在一些模棱两可的情况下(两类别概率接近)做出判断时的不稳定性。在实际应用中,为尽可能减少误诊对于患者带来的各方面影响,还需要采取更多优化措施提升模型性能,并对模型在模棱两可的情况下做出的判断进行合理的限制。
5 总结与展望
本项目全部代码(不包含数据集)已上传至Github仓库,仓库URL地址:https://github.com/Asgard-Tim/Pneumonia-Image-Recognition
5.1 项目总结
本项目基于深度学习技术,结合自编码器和卷积神经网络,开发了一套智能诊断系统,用于快速、高效地识别肺部的CT影像并判断该患者是否患有肺炎(包括COVID-19)。自编码器模块有效去除了噪声,提升了图像质量,而卷积神经网络以其强大的特征提取能力,实现了高精度的分类。本项目在数据预处理、模型设计、网络训练及测试等环节中均采用了创新性的技术方案,最终实现了在含噪声测试集上96.97%和在无噪声测试集上94.57%的分类精度,表现出了较高的鲁棒性和实用价值。同时,系统已通过Flask框架部署为Web服务,能够实时接收CT影像并给出诊断结果,为疫情期间大规模影像数据的快速诊断及基层医疗资源匮乏地区的医疗支持提供了重要的技术保障。
5.2 课程收获与反思
本次选修《智能图像处理》这门课程确实让我学到了很多东西,其实自己之前也自己看过一些机器学习方面的内容,有一定的知识基础与环境搭建经验,但由于各方面原因总是没有系统性的去学习计算机视觉的相关知识,也缺乏足够的实战代码与项目经验。通过这门课程的学习,很大程度上锻炼了我Python的代码能力,也在Coding的过程中不断熟悉OpenCV、Pytorch等库的使用,更在实践的过程中不断加深对于各种算法模型(AlexNet、ResNet、YOLO等)的理解。
本次项目让我完整地经历了从数据集获取、论文调研及算法代码实现,再到代码调试与模型训练测试,最终将模型应用到实际系统中的全过程,在项目实现的过程中收获了很多课程教学与实验中涉及不到的东西,包括数据集的收集、模型的选择以及作为一个完整项目的代码实现等等多个方面,这也是我第一次使用GPU资源去进行。虽然由于时间等条件的限制,在模型选择上并没有进行深入的调研与充分的对比试验,只是基于自己已知的一些知识对于架构较为简单的自编码器模型与卷积神经网络进行了复现与设计,最终模型的分类精度还有一定的提升空间,但是这也为我后续的自主学习打下了一个良好的基础,希望未来我能在计算机视觉方面有更加深入的学习与探索,也感谢老师的耐心指导与悉心教学。
参考文献
[1] Nosa-Omoruyi M, Oghenekaro L U. AutoEncoder Convolutional Neural Network for Pneumonia Detection[J]. arXiv preprint arXiv:2409.02142, 2024.
[2] Ratiphaphongthon W, Panup W, Wangkeeree R. An improved technique for pneumonia infected patients image recognition based on combination algorithm of smooth generalized pinball SVM and variational autoencoders[J]. IEEE Access, 2022, 10: 107431-107445.
[3] Gayathri J L, Abraham B, Sujarani M S, et al. A computer-aided diagnosis system for the classification of COVID-19 and non-COVID-19 pneumonia on chest X-ray images by integrating CNN with sparse autoencoder and feed forward neural network[J]. Computers in biology and medicine, 2022, 141: 105134.
[4] García-Ordás M T, Benítez-Andrades J A, García-Rodríguez I, et al. Detecting respiratory pathologies using convolutional neural networks and variational autoencoders for unbalancing data[J]. Sensors, 2020,20(4): 1214.
[5] Xia Y. Enhanced Pneumonia Detection in Chest X-Rays Based on Integrated Denoising Autoencoders and Convolutional Neural Networks[J].
[6] El-Shafai W, El-Nabi S A, El-Rabaie E S M, et al. Efficient Deep-Learning-Based Autoencoder Denoising Approach for Medical Image Diagnosis[J]. Computers, Materials & Continua, 2022, 70(3).
[7] Rana N, Marwaha H. Auto encoder-guided Feature Extraction for Pneumonia Identification from Chest X-ray Images[C]//E3S Web of Conferences. EDP Sciences, 2024, 556: 01011.
[8] Ankayarkanni B, Sangeetha P. An Autoencoder-BiLSTM framework for classifying multiple types of lung diseases from CXR images[J]. Multimedia Tools and Applications, 2024: 1-30.
[9] 孙敬,丁嘉伟,冯光辉.一种基于自编码器降维的神经卷积网络入侵检测模型[J/OL].电信科学,1-7[2025-01-05].
[10] 张淙越,杨晓玲.基于卷积神经网络的新冠肺炎CT图像识别系统[J].电脑与信息技术,2022,30(03):12-14+40.