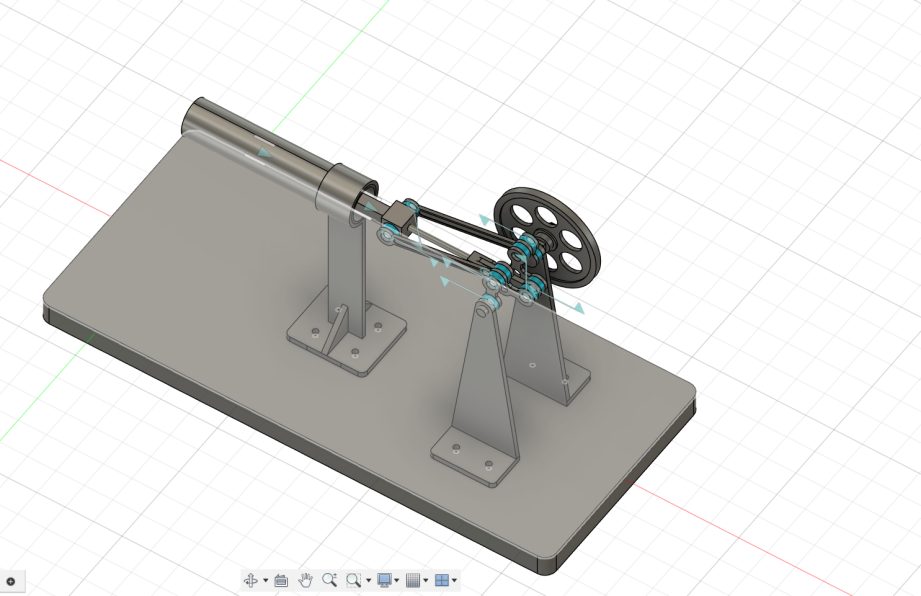
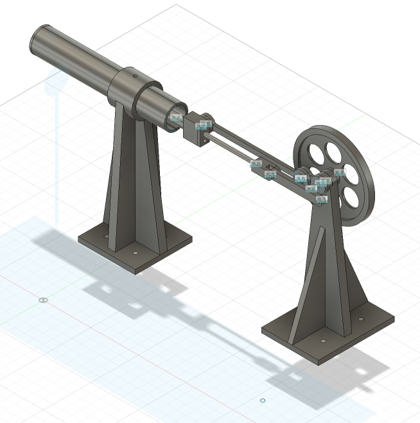
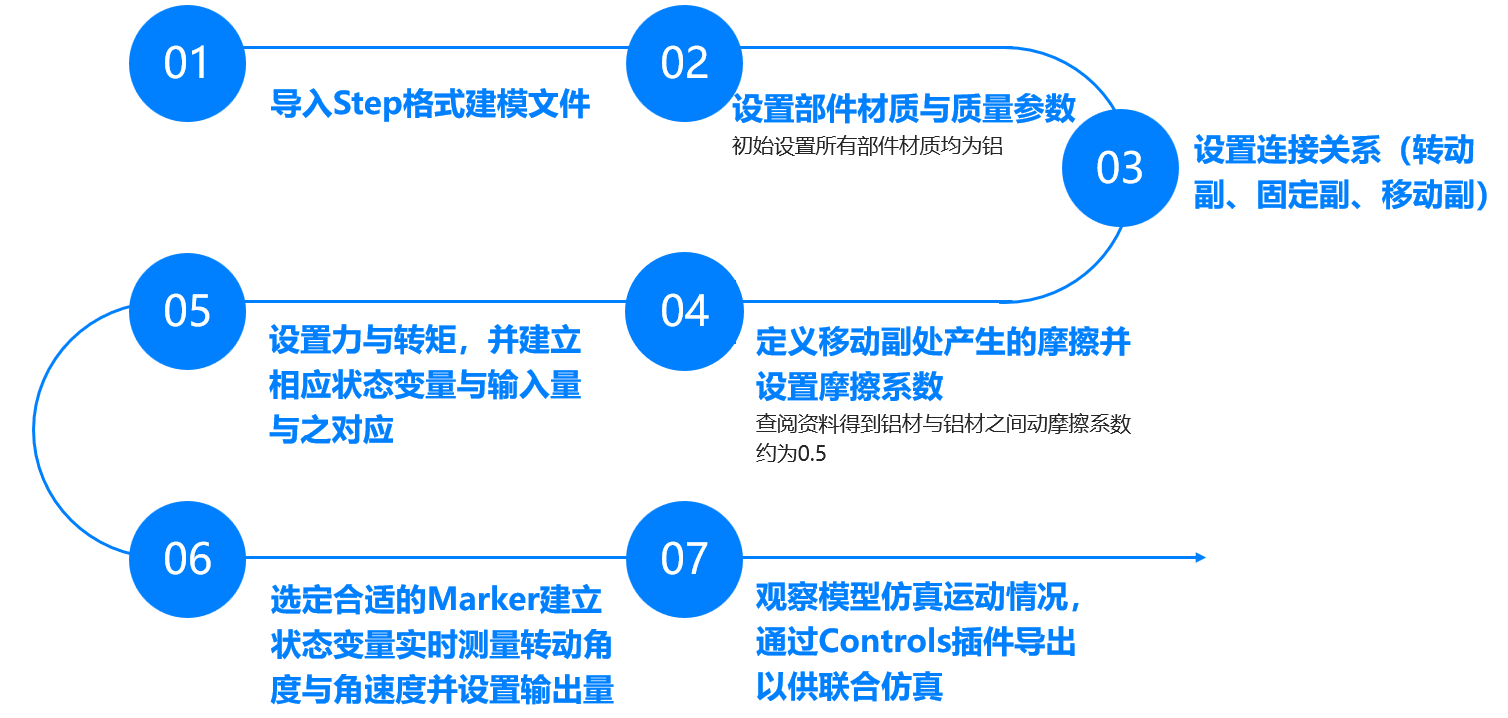
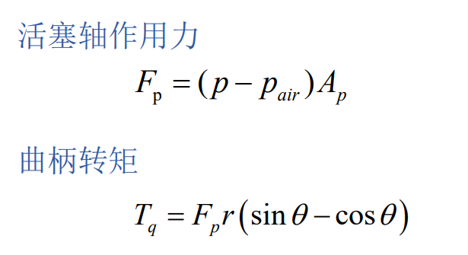1 设计过程与方案概述

任务要求为设计一个斯特林发动机，大部分零件采用金属加工的方式，最后能够提供0.5w的功率输出。有以下方面的目标：设计一个能够满足做功要求的气缸，设计与之配套的连杆机构，设计动力输出装置。

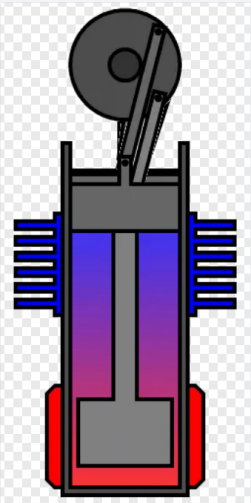
针对以上要求，我们先采用β型发动机作为模板进行设计，先设计气缸，后进行相关的理论计算和仿真，最后根据计算和仿真结果对设计进行修改，对修改好的设计进行加工，经过实地组装测试之后再对出现的问题进行分析和修改，最后得到能够满足要求的发动机。

中途进行测试的时候发现β型气缸相对于α来说加工有一定难度，即满足公差设计的加工也可能由于做功活塞和配气活塞之间的差距导致漏气，使得整体运行时存在一定的气体溢出，并未能推动活塞做功。所以我们后续改用了β，α两种发动机并行设计的方式，先在α型上测试成功后，再利用吸取到的经验和设计方式来完成β的设计。

最终测试结果如下：β发动机不能够正常运行，但是气缸的密封基本完成，α型发动机能正常运转，且能够点亮一个额定功率为0.5w的电灯泡，经电表测试约为一个3.2V的电压源，但在实际测试时，没有能够达到0.5W的输出功率。

2 气缸设计与加工设计

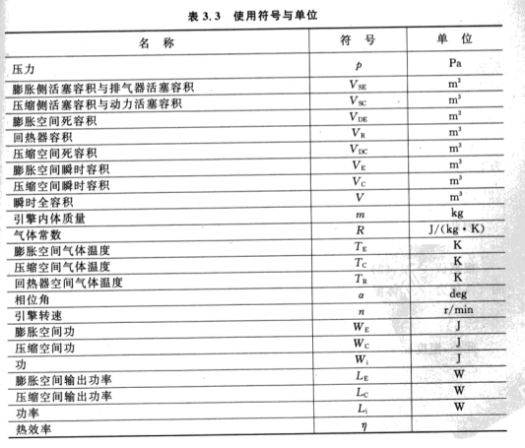
2.1 气缸设计与做功计算

单独对气缸进行分析和设计时，采用的计算方式是先估算转速和单个做功冲程所能做的功，作为一个机械功的功率来源，要先保证功率来源大概约为0.5w的3到5倍，使得为后续机械装置带动发动机皮带留够足够的功率。

气缸的设计关键在于密封性，体现在加工方面就是公差的设计，如果产生的偏差导致气缸和活塞的成品配合不好，则在加热过程中气体就会溢出，使得整个气缸无法产生较大的温差，使得内外压强之间的差距很小，自然无法推动活塞对外做功。在进行气缸设计时，气缸的直径也是一个关键的指标，如果直径过大，加热时间过长，则无法充分受热，无法产生推力，当直径过小时，压强产生的推力会小很多，影响最终的输出功率，我们根据之前学长的发动机进行了简单的估算，直径在1cm-2cm为宜，而公差设计要求气缸为负公差-0.02mm,活塞为正公差+0.02mm，即使加工得没有特别准确，也可以保证通过简单的手动打磨和不断测试可以使得气缸和活塞刚好匹配。

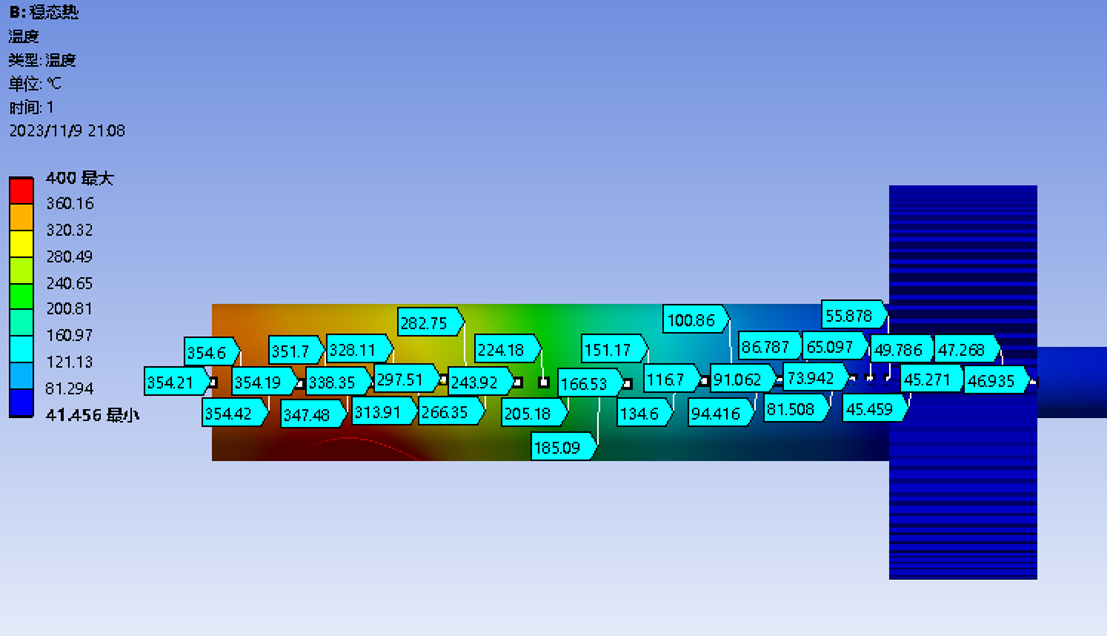
由于高度对称的模型气缸设计，可以建立温度随模型位置的函数t(x)，以及空气密度随温度变化的函数ρ（t），则根据理想气体方程PV=nRT，进行变形，得到PV=ρSX/MRT,调整位置得到，PV=S/MR*(ρXT)，变为微分形式可得到，PSdx=S/MR*(ρ（x）T（x）dx)，变形得，FSdx=S/MR*(ρ（x）T（x）dx)即dw=S/MR*(ρ（x）T（x）dx)，由于该过程恒处于大气压下，将各物理常数，代入积分后可直接得到结果。

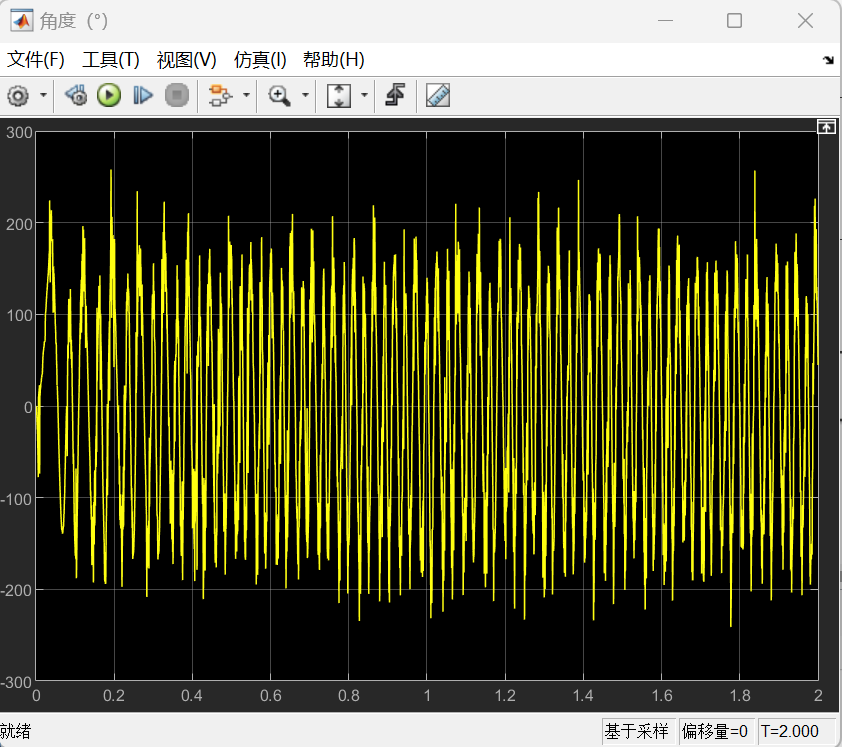
以下为matlab计算步骤：先根据图进行采样，计算并拟合出温度位置曲线T(x),再代入公式进行计算，β型的计算过程过程如下图：

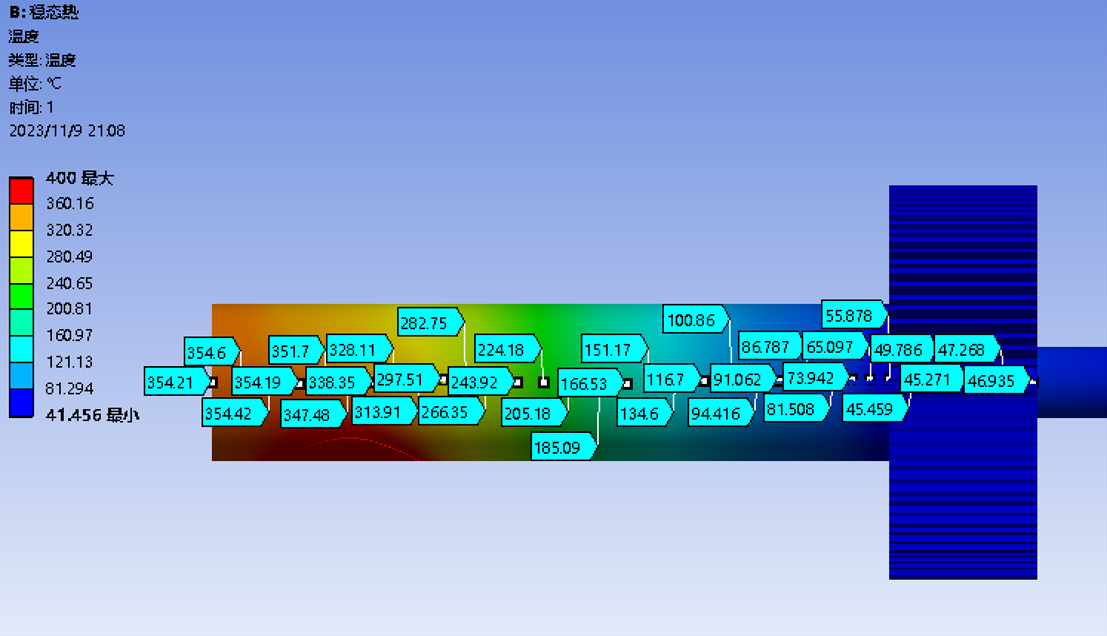
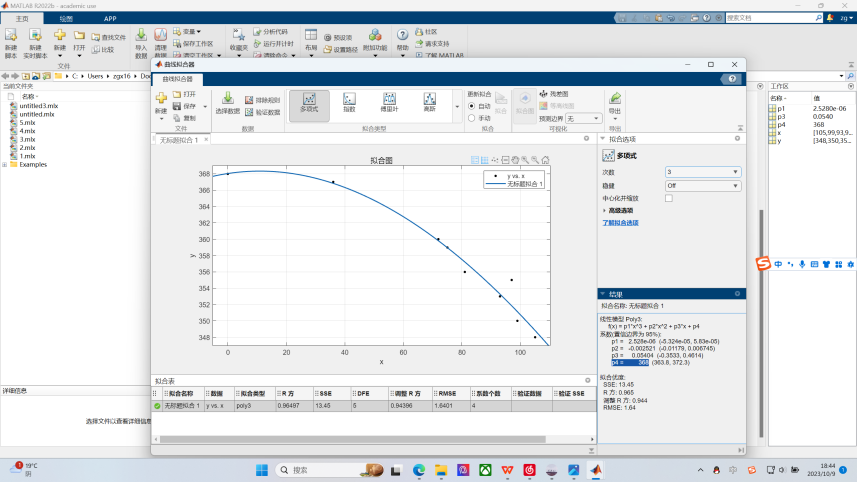
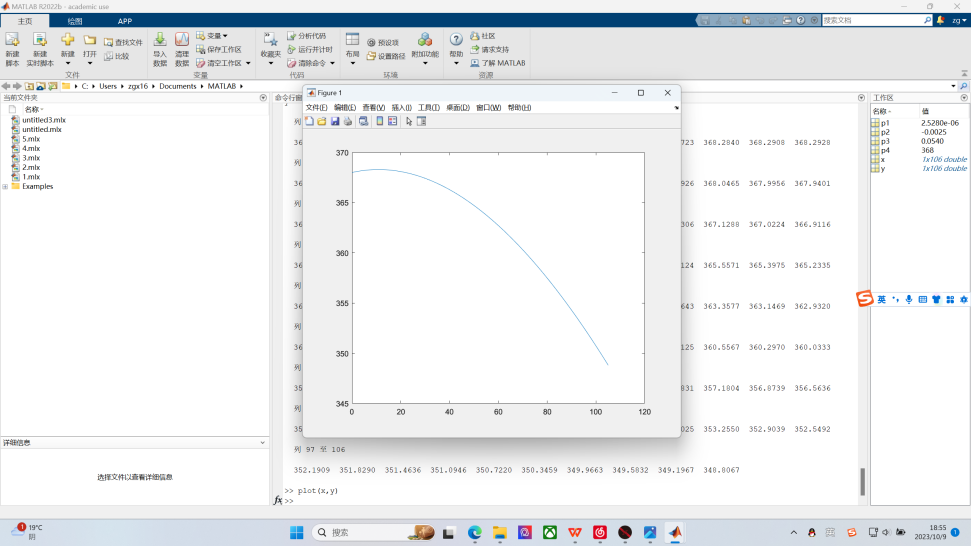
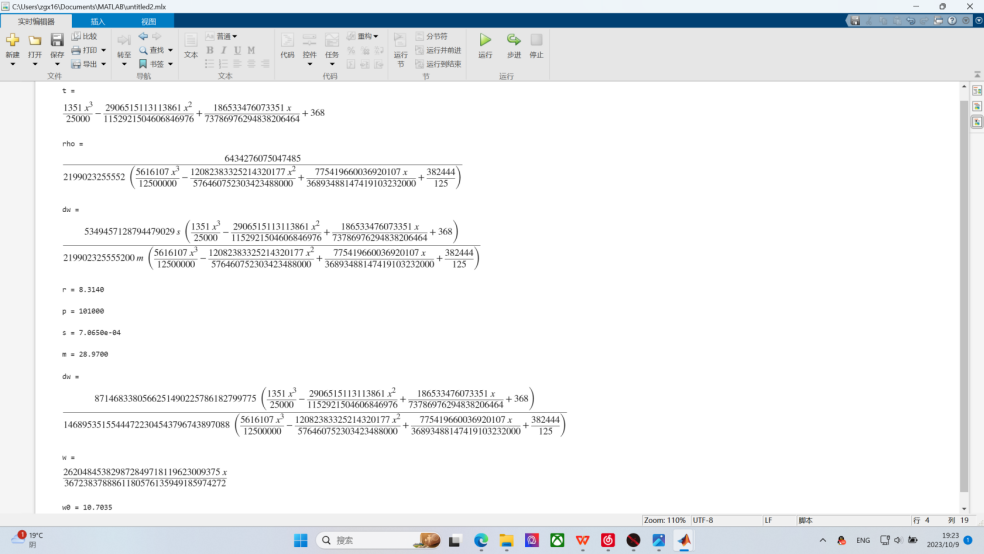
则单次做功冲程能够对活塞做功1.07J，也就是说在转速约为5-8转每秒时，完全可以提供足够的功率带动后续的传动装置和发电机。

对于α的计算如下图：

{width=”5.759722222222222in”
height=”2.3715277777777777in”}

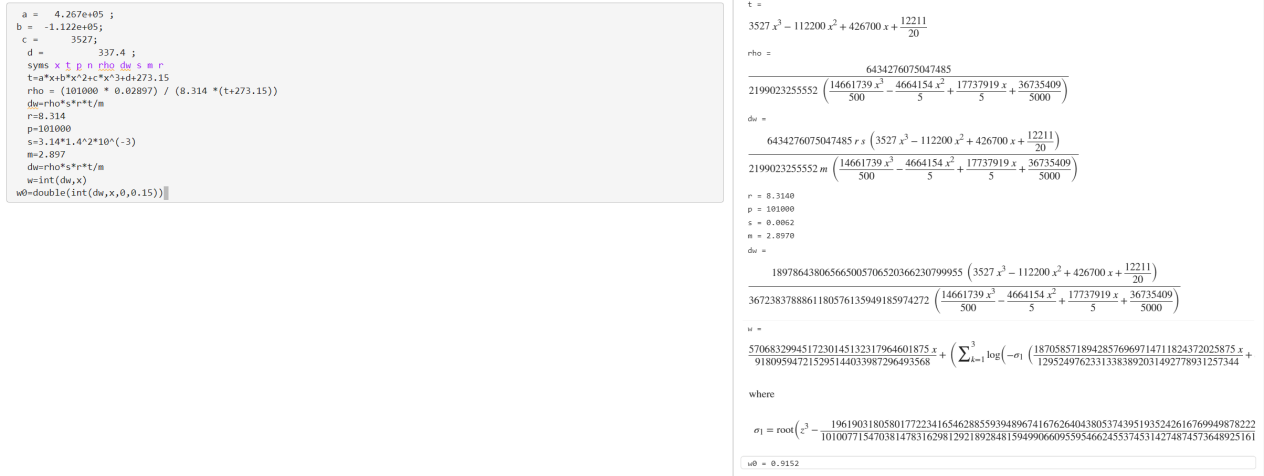
则单次做功冲程能够对活塞做功0.9152J，也就是说在转速约为8-12转每秒时，完全可以提供足够的功率带动后续的传动装置和发电机。

2.2 密封、公差、轴承、振动的设计

2.2.1 振动

在经过组装测试后，我们观察了其运动时的振动情况，并对振动来源进行分析，从而提出了一些减少振动的方案。

对于β型的振动分析：

{width=”2.42882217847769in”
height=”3.2392957130358706in”}

可以看到，主要振动的来源在于两连杆间半个周期收活塞的推力传导产生对于中轴形成的错位的力矩，此外，飞轮转动使得由角动量产生的对抗上述力矩的回正力矩（类似惯性力）。综合上述过程，整体振动的来源就是上述周期性力矩的合力矩，但由于存在相互抵消的部分，只要飞轮和连杆的设计配合比较好，就能减小振动的影响，即飞轮设计的大一些，连杆的宽度设计得小一些。

对于β型的振动分析：

可以看到由于α冷热缸分开且加入回热器后，会由于气体做功出现两组相反的周期性旋转力矩，且时间错开，这导致会产生一个稳定的围绕支撑杆的左右转动进而引起振动，且最终呈现的合力矩会使在如上图方向时使发动机整体逆时针旋转，对整体的稳定性产生极大的影响。对此我们采用了相应的解决方案，在下部固定橡胶的减震底座，使底座与地面摩擦力增大，不使其绕固定轴进行旋转，同时减少其振动。

2.2.2 轴承

（1）型号选择

根据α、β斯特林发动机上需要使用轴承的部件及要求，我们分别采用了两种轴承：深沟球和推力球轴承。两种使用场景下，轴承都只收到径向压力，而α型上的轴承用来满足转轴高速转动需求，β型上的轴承用来连接不同平面内的连杆、飞轮。

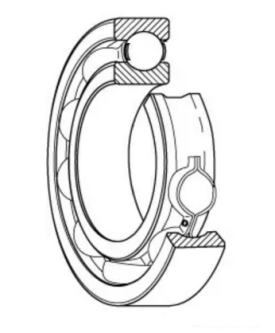
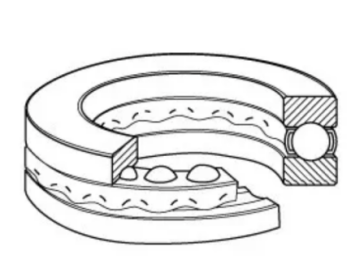
（2）寿命分析

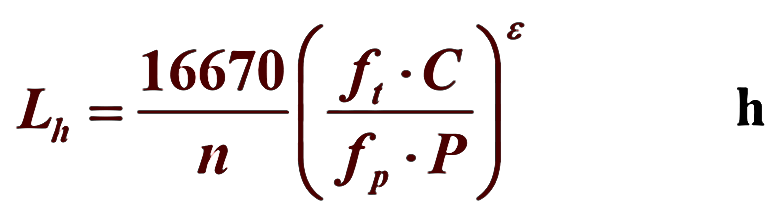
1．深沟球轴承寿命分析

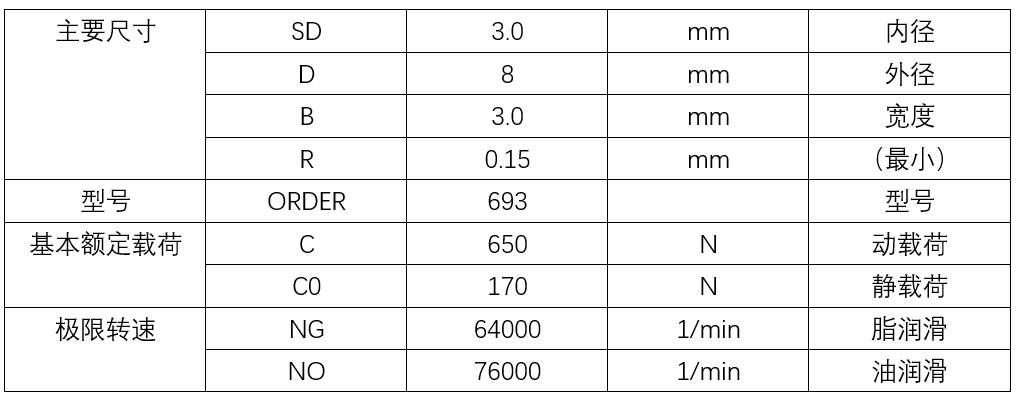
轴承属性见上表（厂商提供）。工作温度小于120℃，ft=1。查表后fp取1.1。

F_R由G，Fn两部分构成。其中G是飞轮重力，Fn是向心力，积分可得Fn=2/3*πρω^2*r^3H，H(厚度)=0.008m，r=0.025m，ρ=2.7*10^3kg/m^3，ω实测为60πrad/s。因此P=F_R=G+Fn=0.46868N+25.503N≈25.97N。

带入公式可得，L_h=109096.1小时。

2．推力球轴承寿命分析

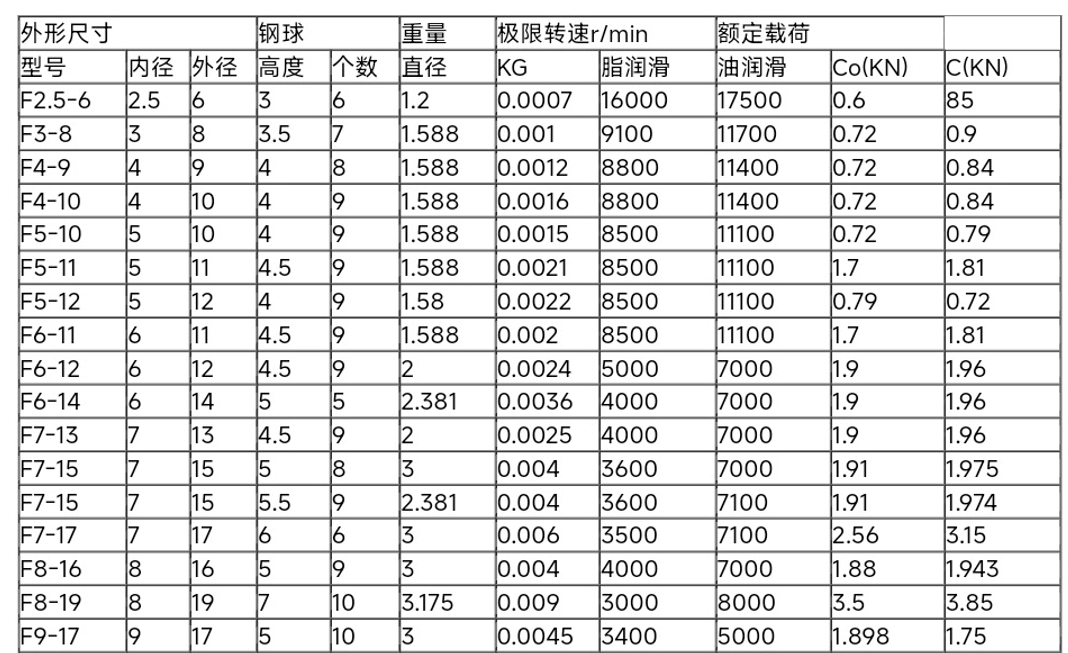
轴承属性见上表（厂商提供）。工作温度小于120℃，ft=1。查表后fp取1.1。F_R由G，Fn两部分构成。其中G是飞轮和轴重力、连杆重力分力，Fn公式同上。H(厚度)=0.004m，r=0.04m，ρ=2.7*10^3kg/m^3，ω假设为66πrad/s。因此P=F_R=G+Fn=0.4259N+62.237N≈62.66N。

带入公式可得，L_h=186713.1小时。

3 热力学仿真与斯特林循环计算

3.1热力学仿真

该部分主要是将四个冲程的斯特林循环带入，通过得到气缸的pv图和相关的力矩变化图线，从而更好地评估设计的情况。

计算的核心在于计算当下各设计在转动时的功率，以及在指定转速下的功率，最后调整传动装置的连杆比，以及活塞的运动空间，以及计算一次做功的最大功是否能驱动飞轮以指定的预测转速进行转速，从而进行调整。

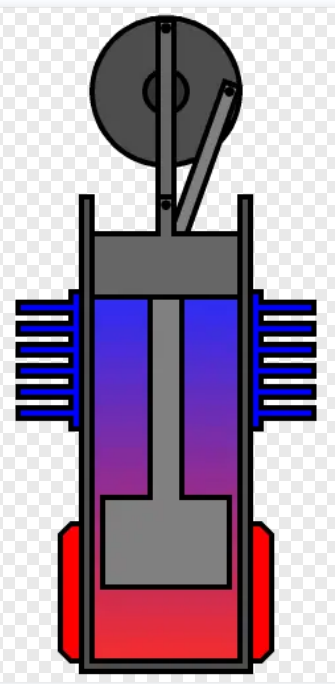
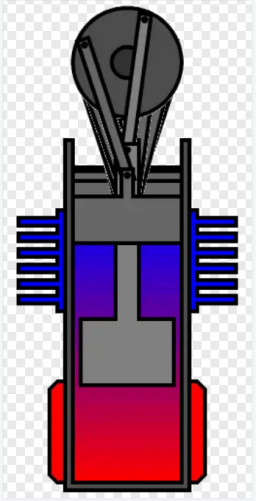
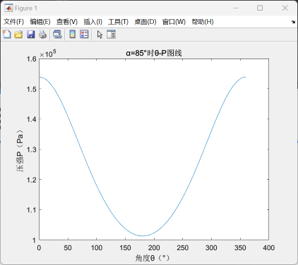
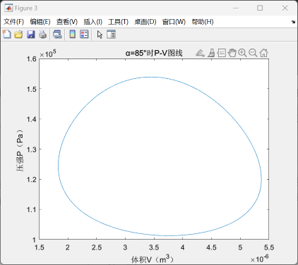
β型发动机的计算结果如下:

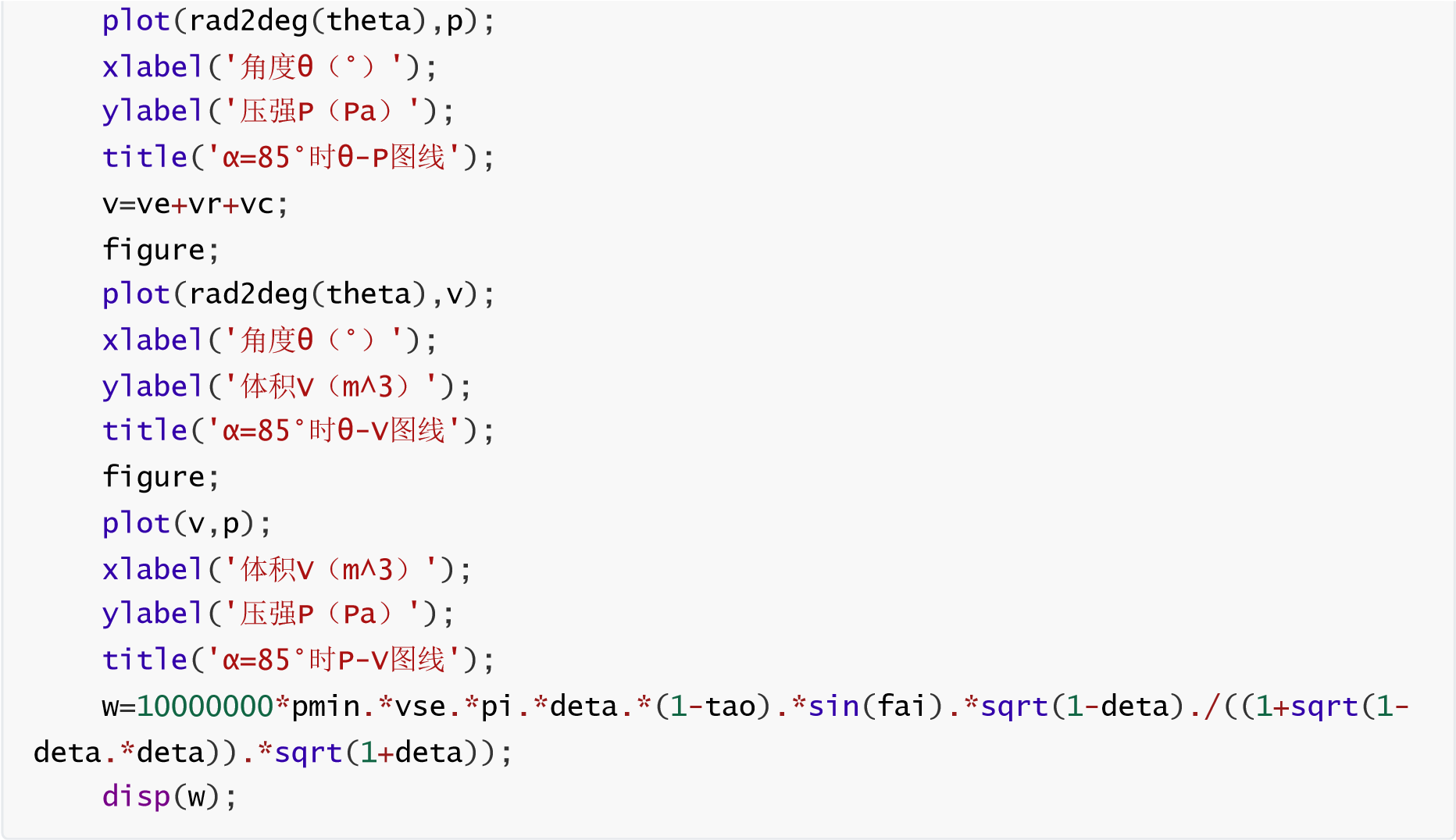
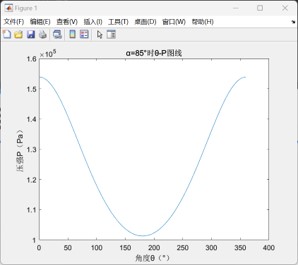
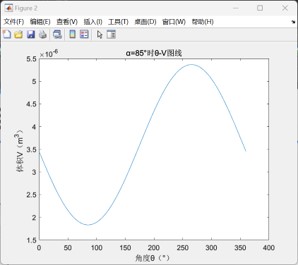
计算出单次循环做功为0.0523J，若要达到设计目标的0.5W功率要求，需要转速达到：rmin=0.5*60/0.0523≈573.6rpm。

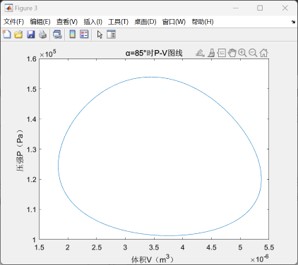
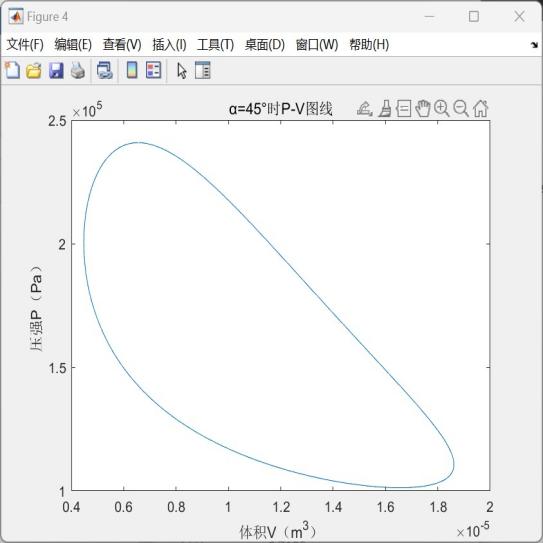
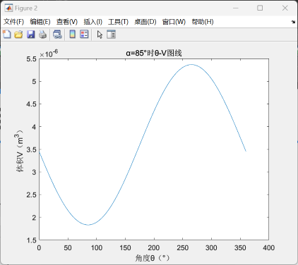
此外，以上设计参数所得到的P-V图线偏扁圆形，与常见的P-V图线形状有一定差异，这主要是与设定的初始相位角有关，若将相位角改为45°，则可以得出如下P-V图线，并可计算得出此时对应的单次循环做功为0.0608J，较先前有所提高；但在β型斯特林发动机中，相位角是由相关零件的设计直接确定的，故在后续仿真中仍保持相位角α=85°的设定。

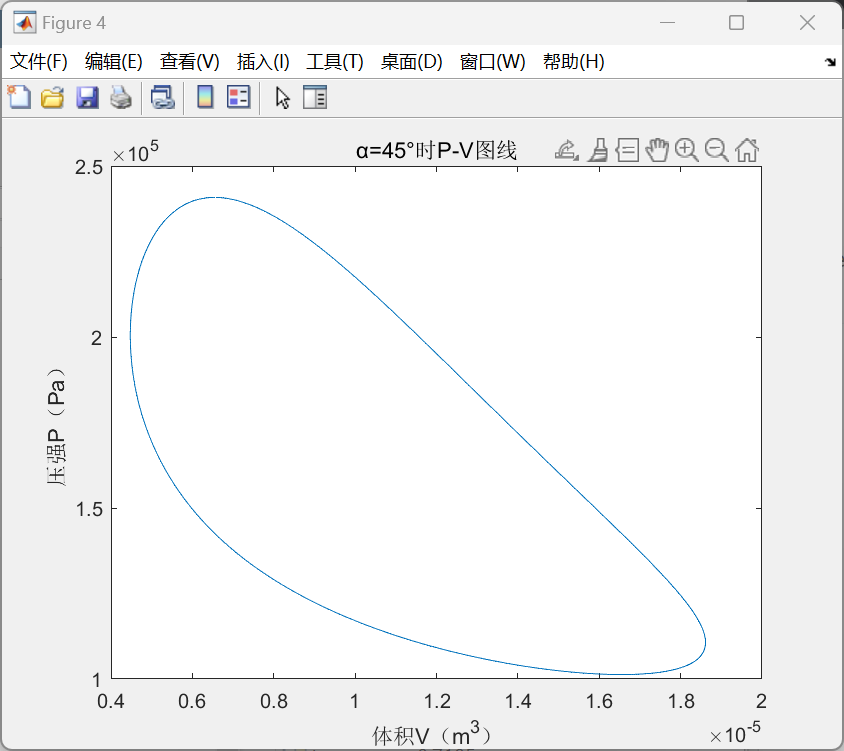
α型的计算结果如下：

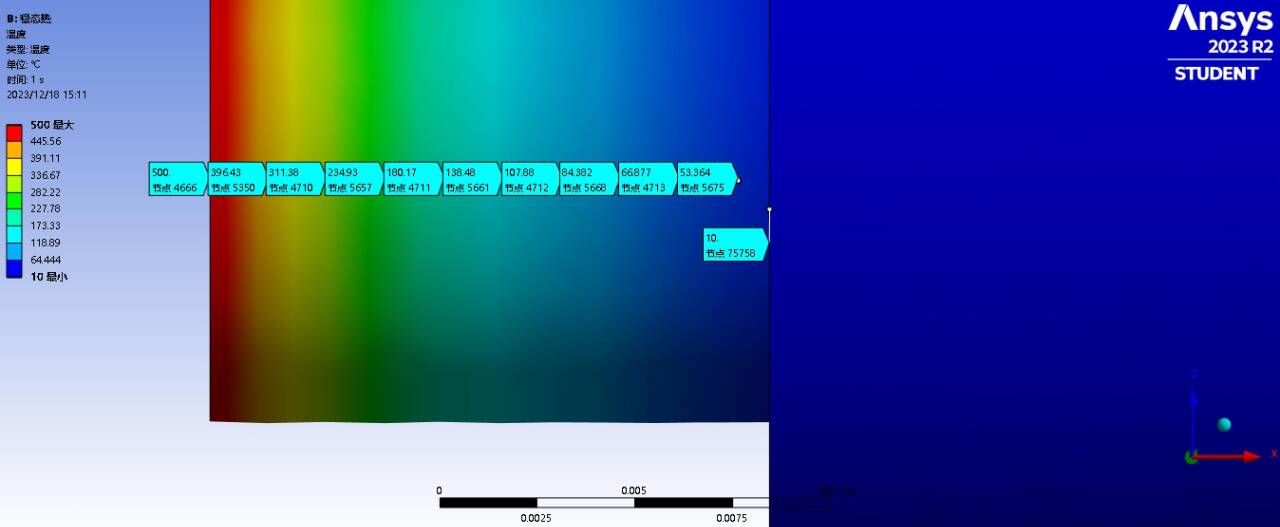
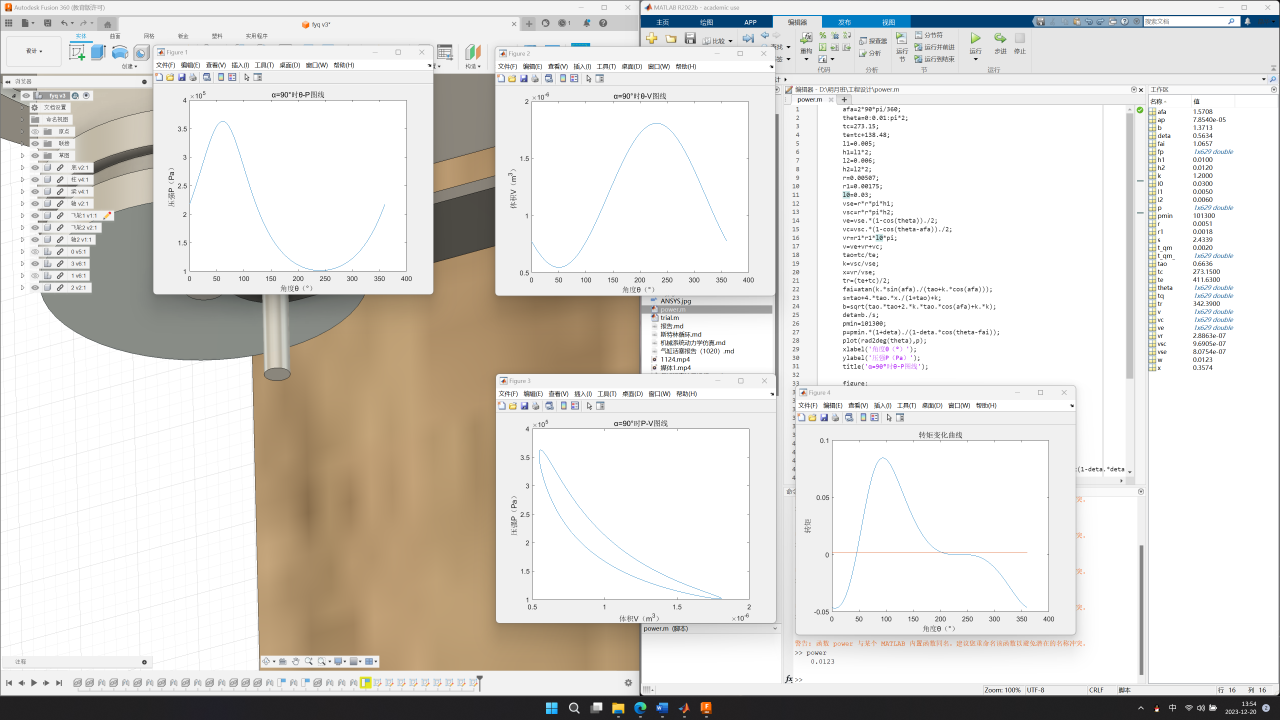
计算出单次循环做功为0.0172J，若要达到设计目标的0.5W功率要求，需要转速达到：rmin=0.5*60/0.0172≈1744.2rpm。

可以看到的是，α型由于回热器的引入，P-V图线的情况要好的多，整体效率有不少的提升，但是由于采用了更小的活塞面积，单次做功的大小减少了，经查询实际情况下相同气缸面积大小的斯特林发动机的转速，大多在两千转以上，则能够满足我们实际的做功要求。

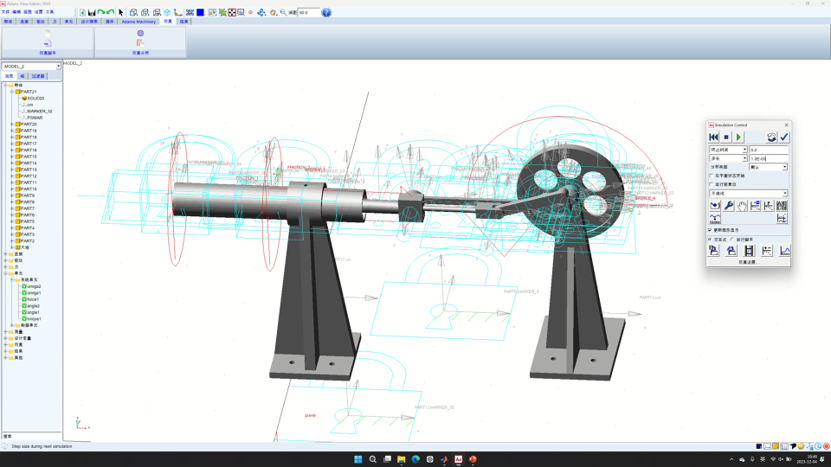
3.2 Adams仿真结果

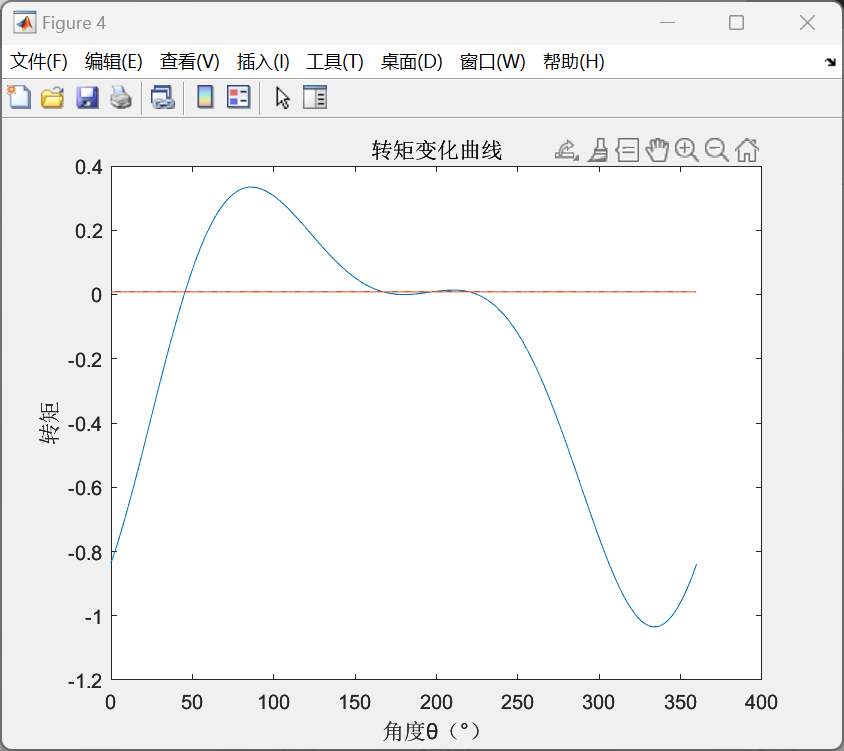
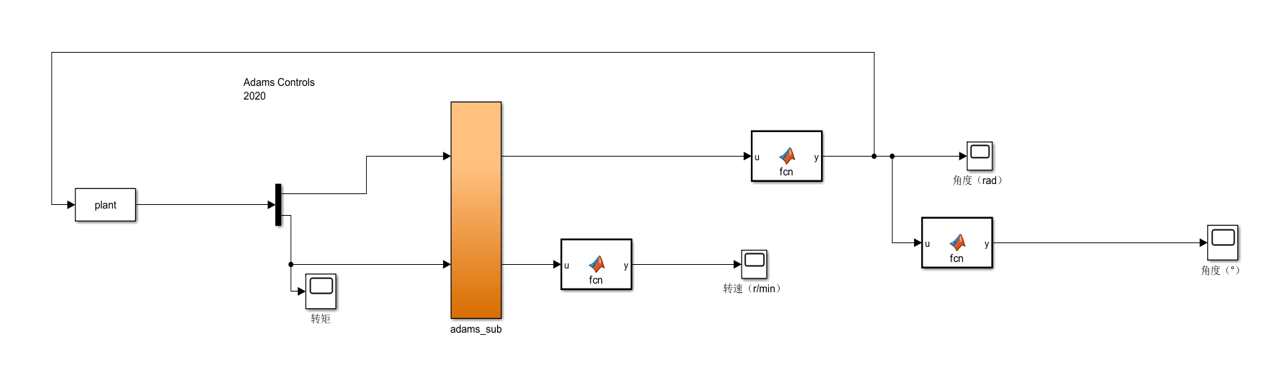
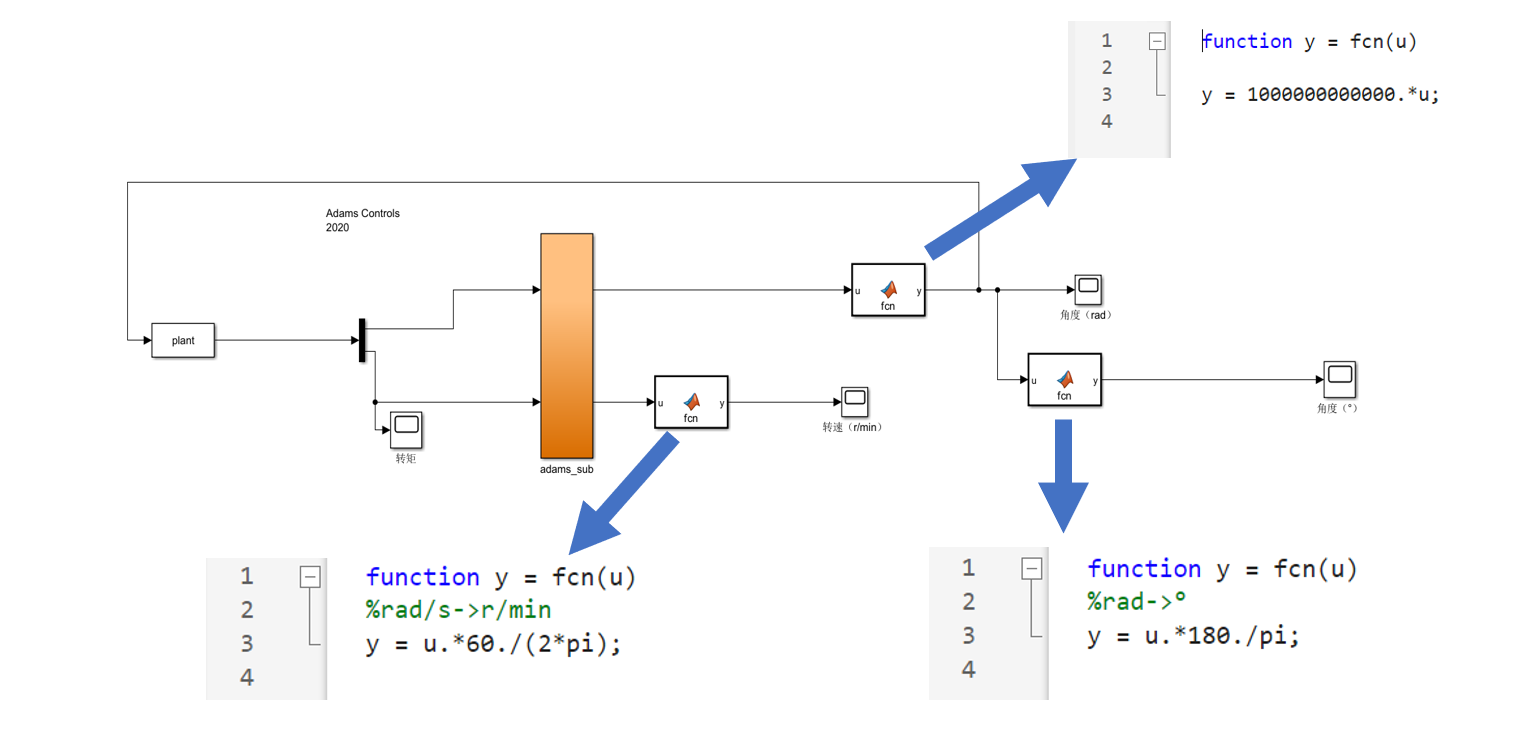
计算推力乃至转矩关键就要计算气缸内密封气体对于活塞产生的压强，并用相应的公式可以根据实时的飞轮转动角度给出对应气压P的计算。于是，通过对于上述热力学斯特林循环代码的简单改写，结合推力与转矩的转换，再利用力的变化或者转矩的变化，得到整个运动情况的仿真如下：

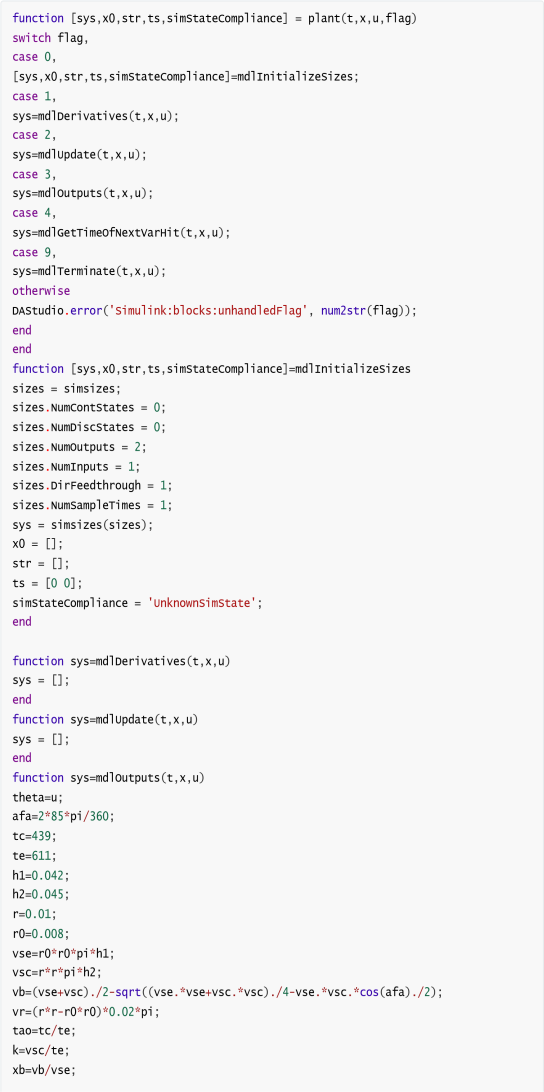
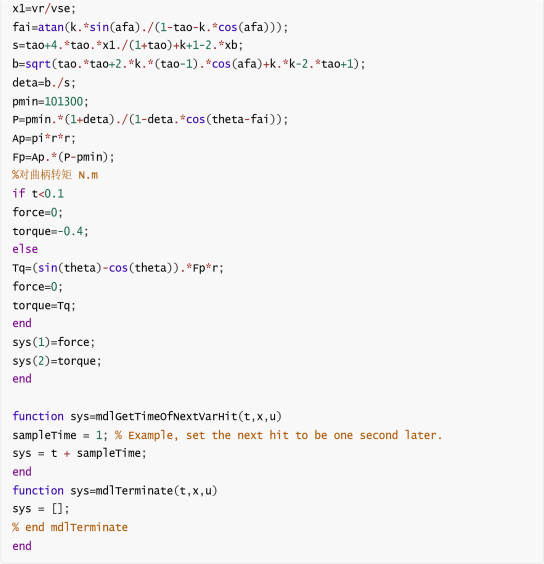
除此之外，由于两个仿真系统之间的运算单位不统一，在将Adams中角度单位改为rad（弧度），长度单位改为m后，仍然需要对相应的角度与转速数据进行单位上的换算处理（如下图所示），从而可以得到数量级正确的数据图线。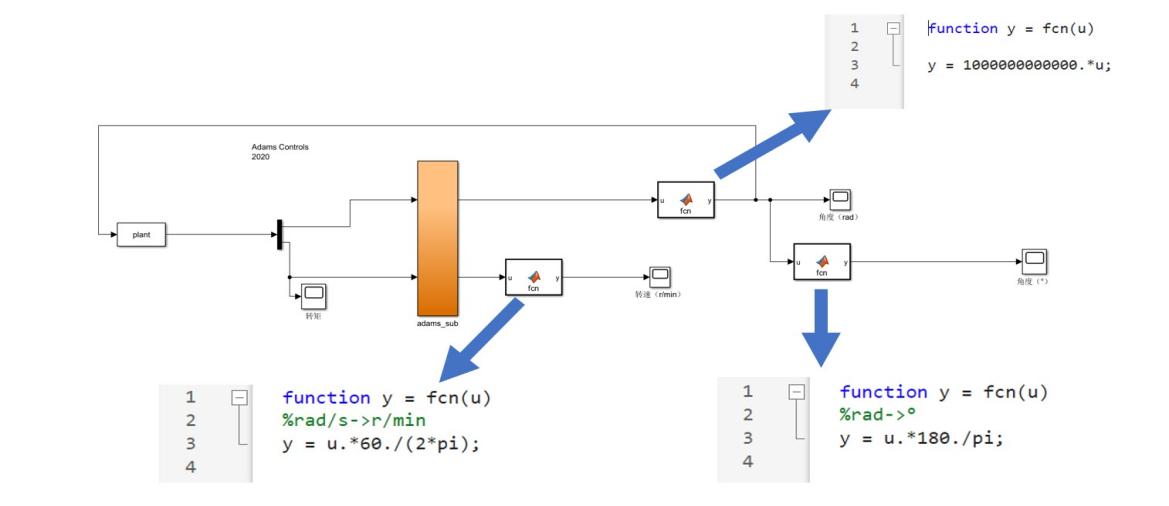

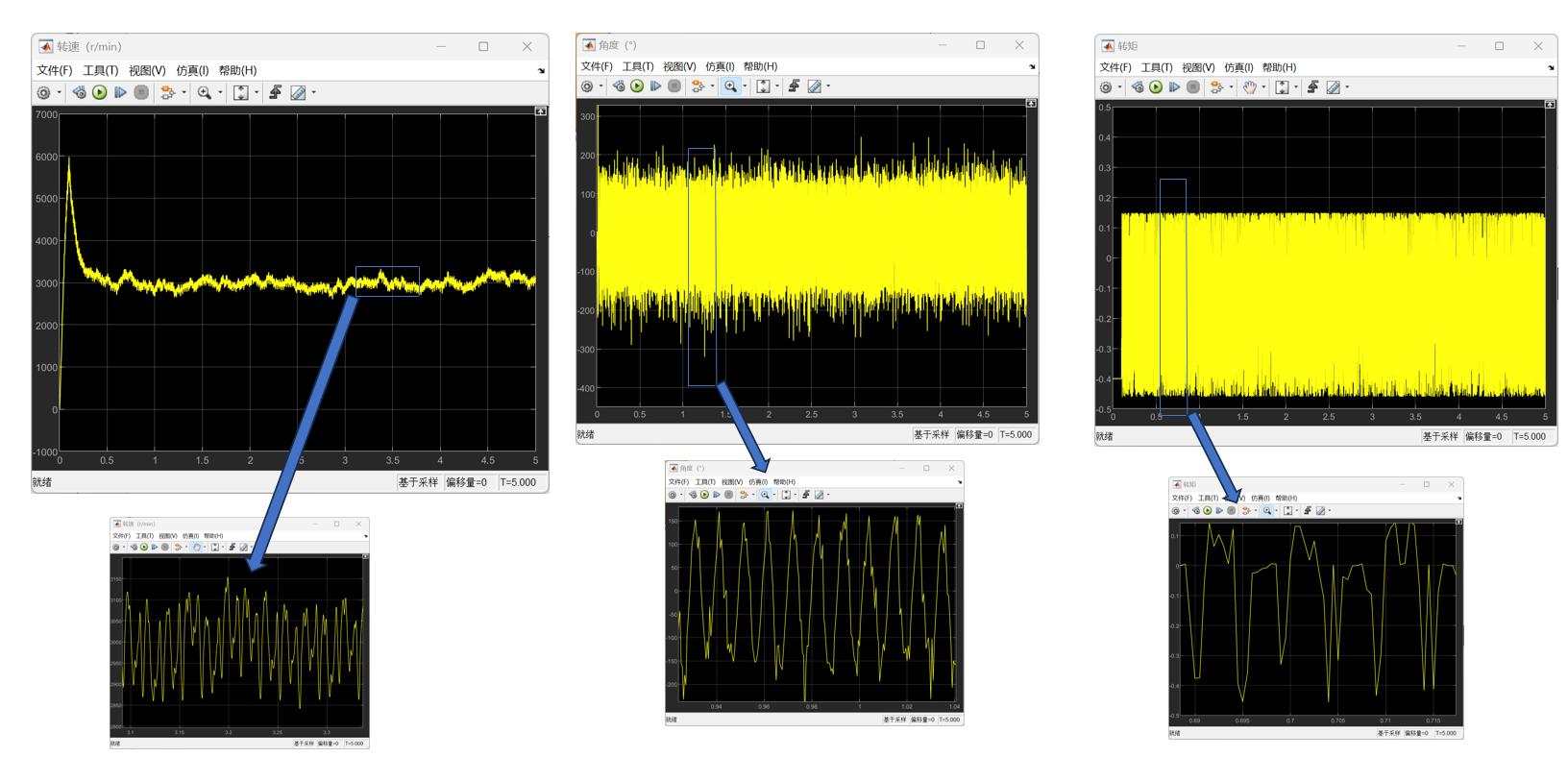
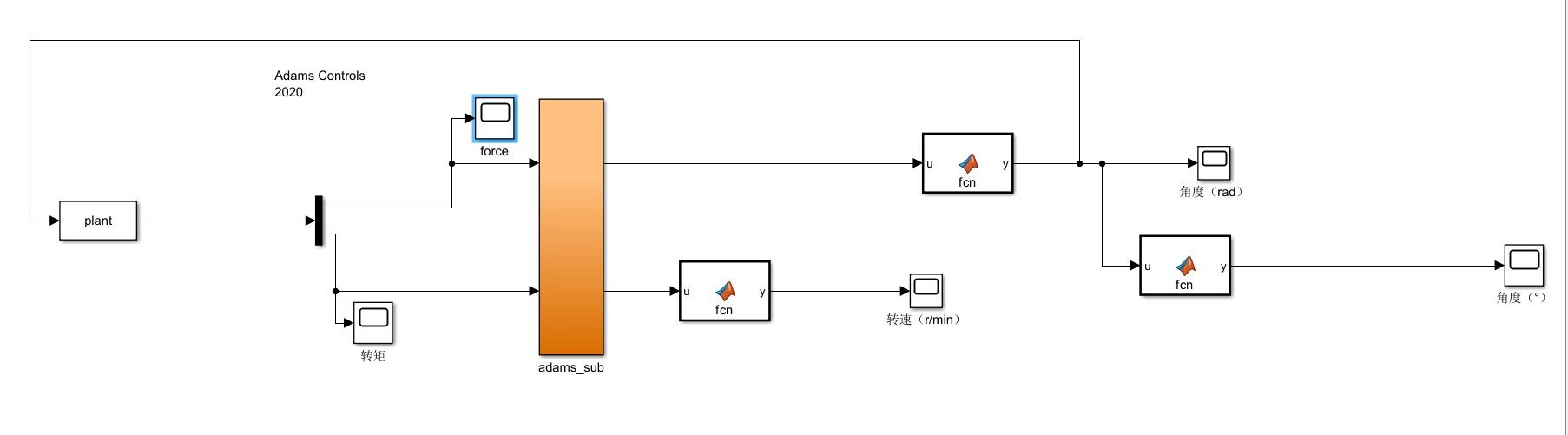
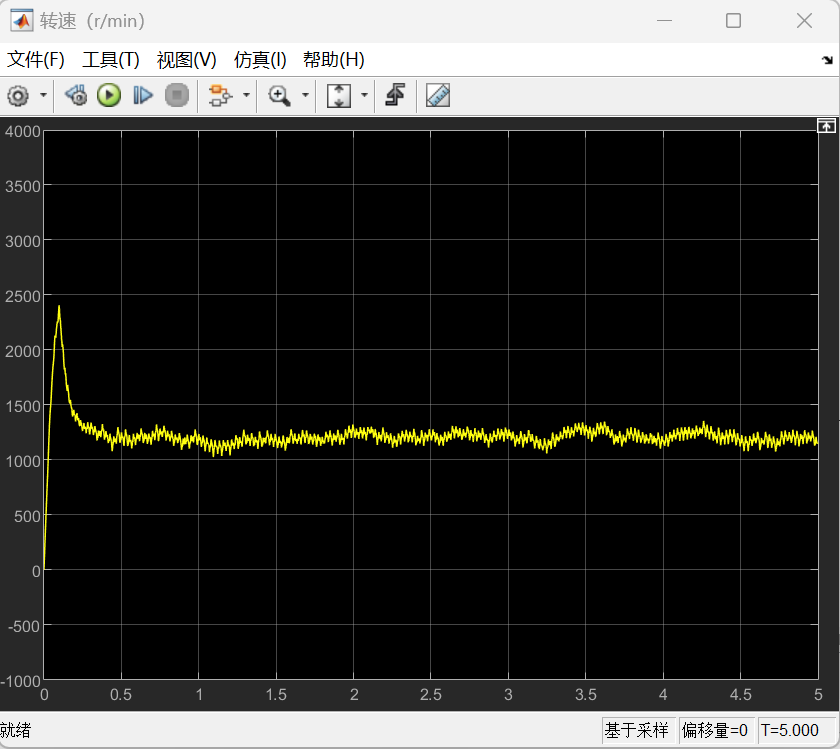
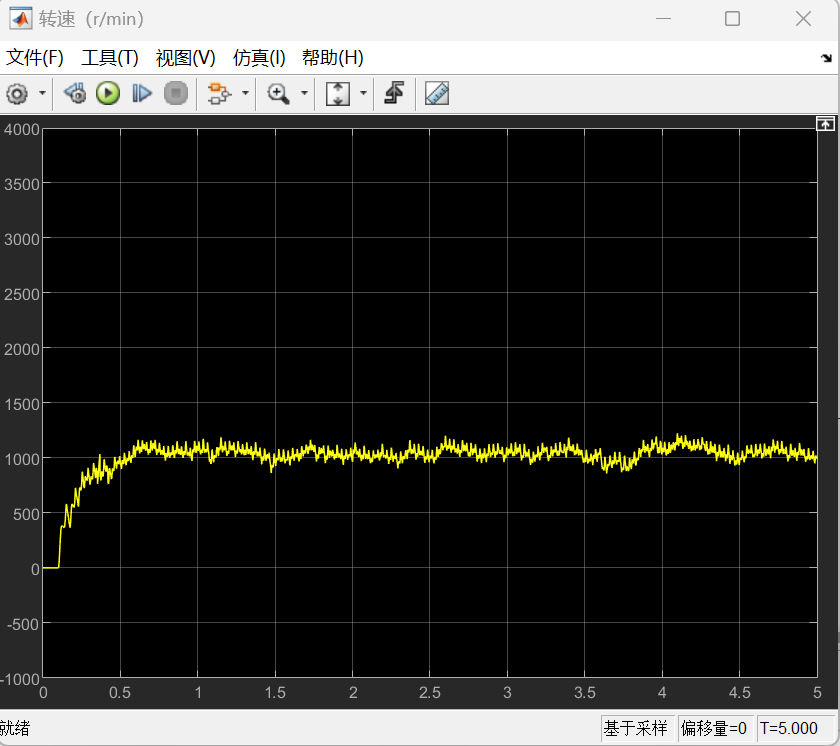
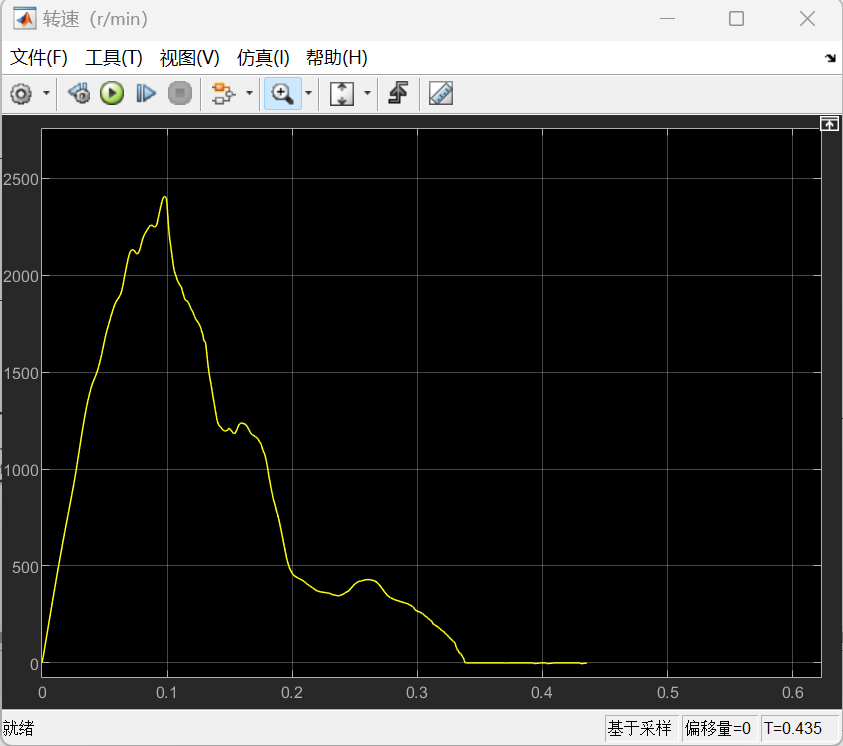
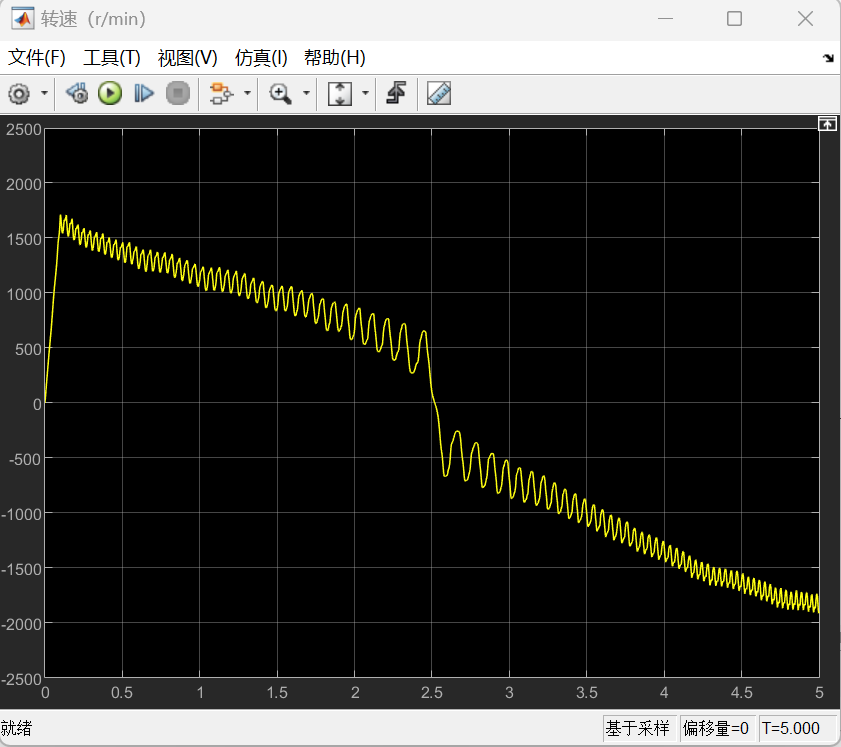
则对于β型的仿真结果如下：

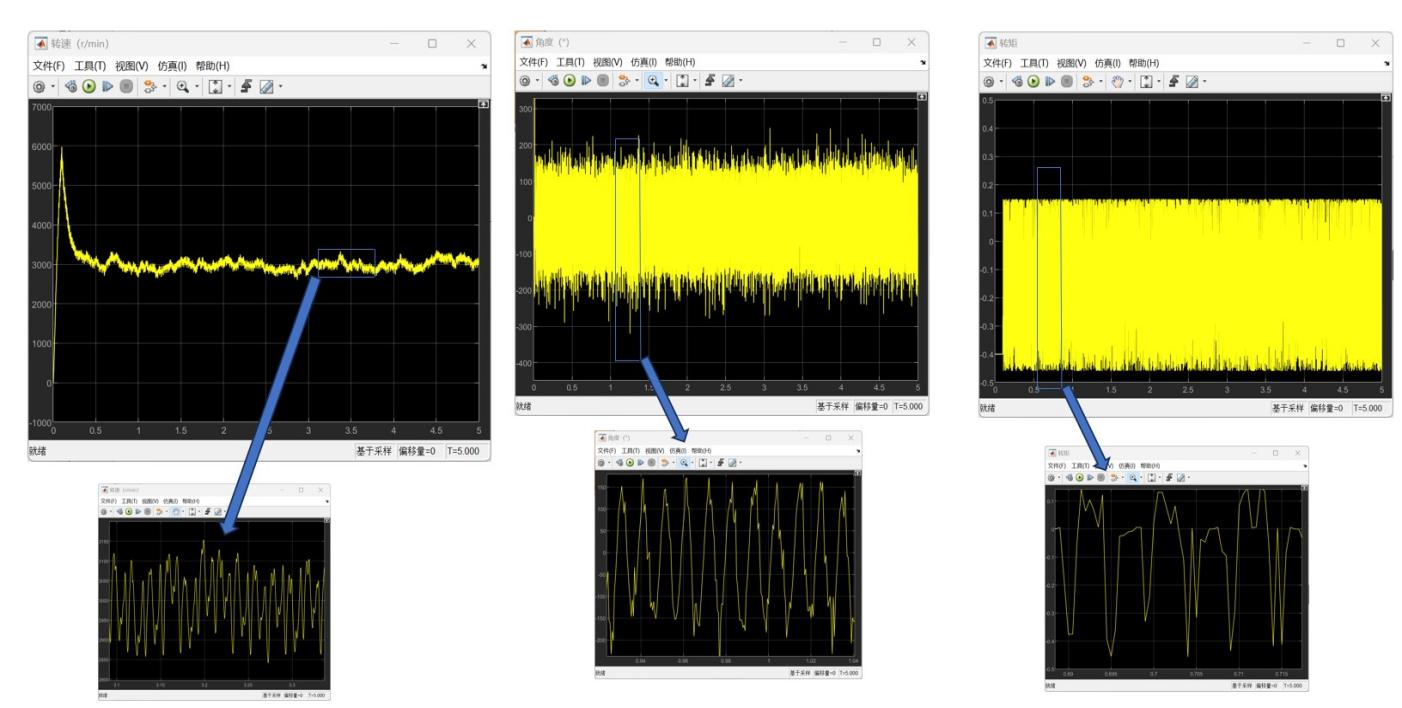
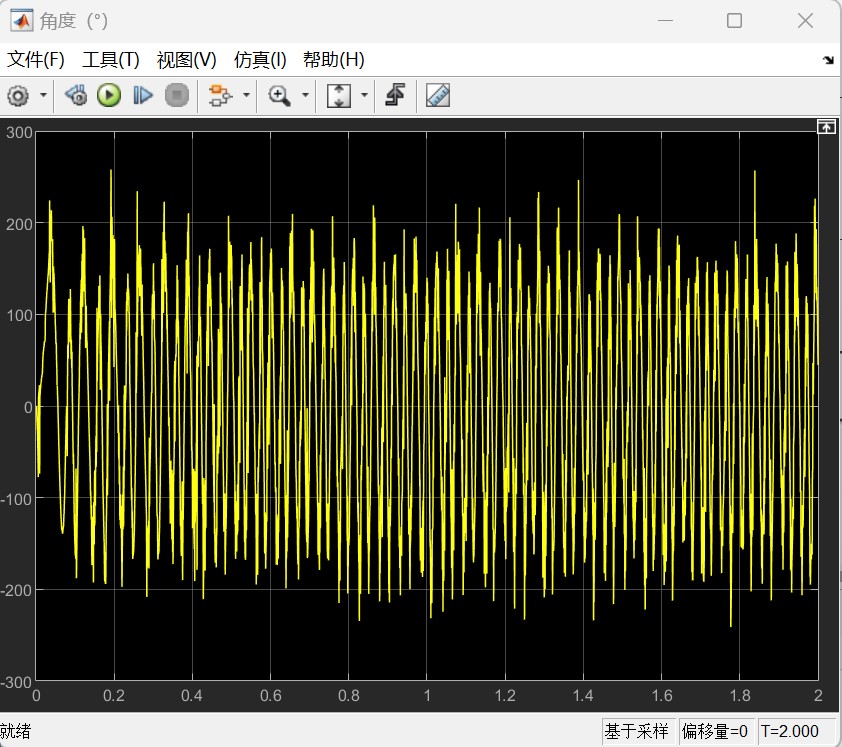
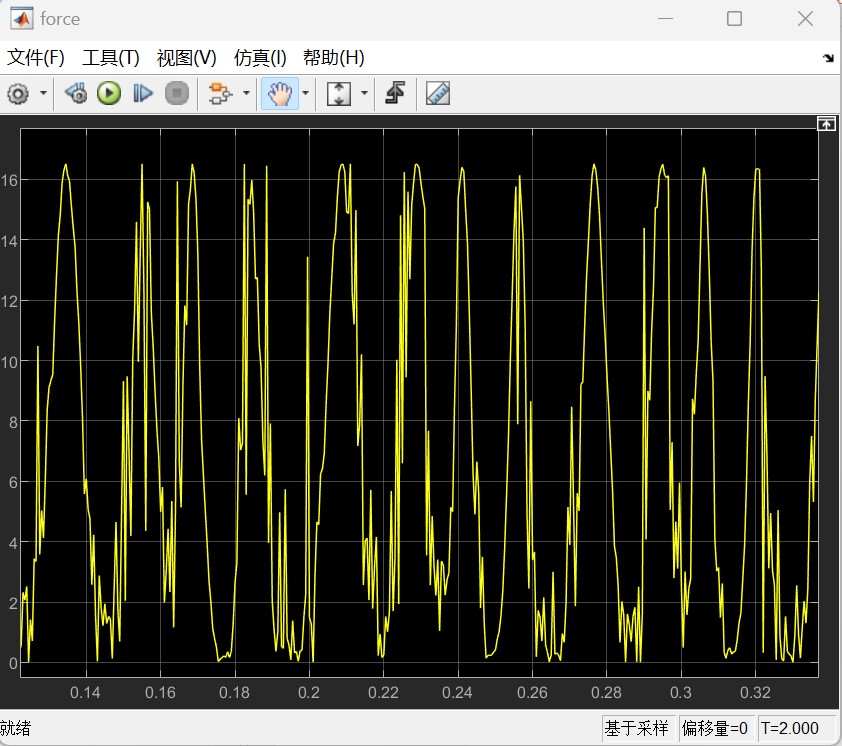
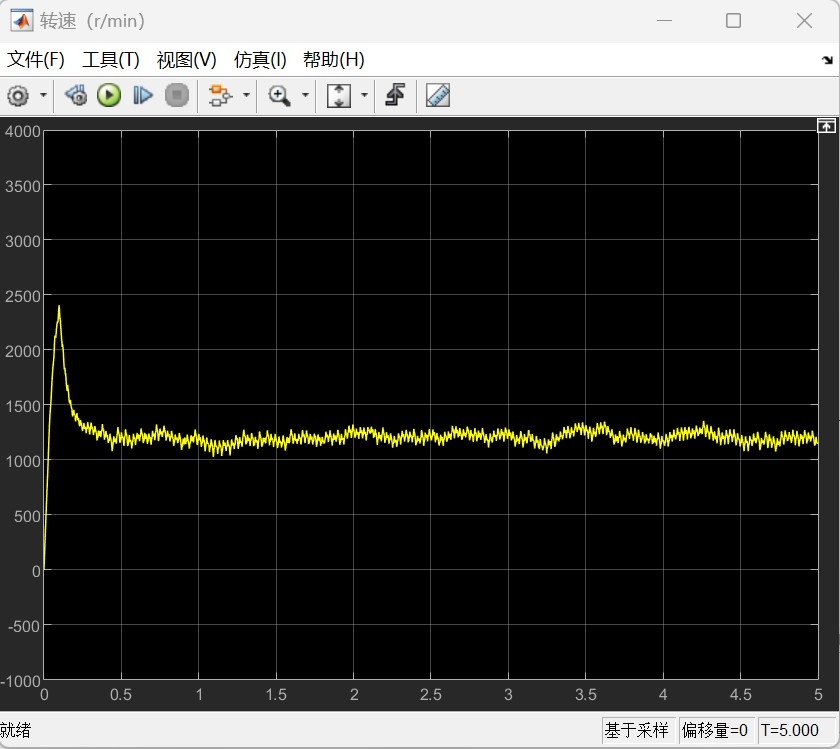
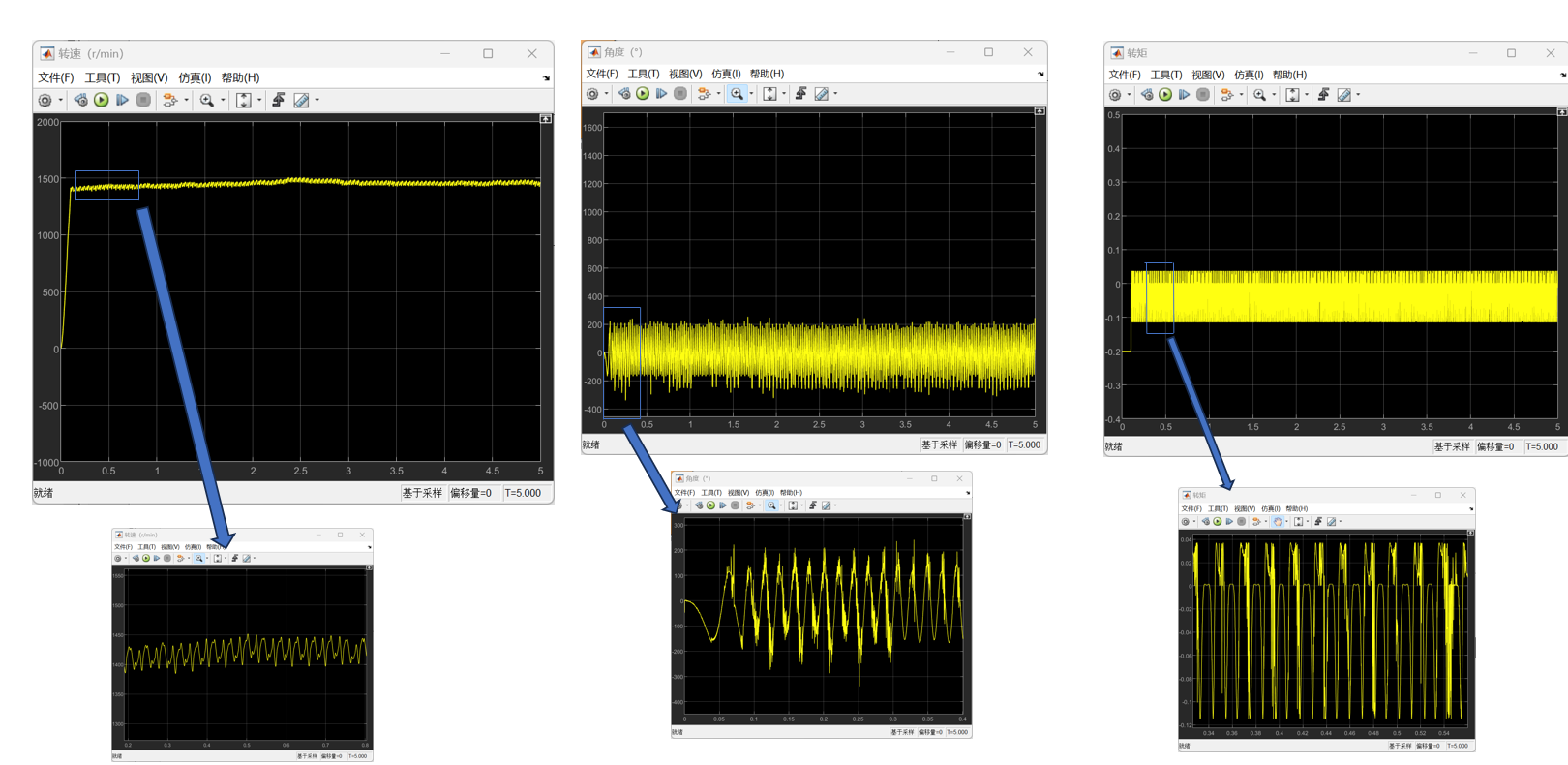
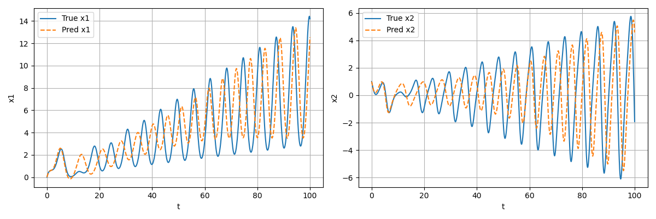
α型的的仿真结果如下：

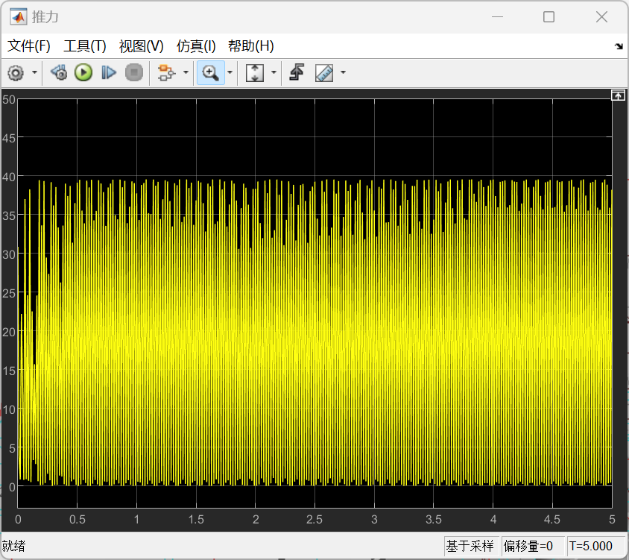
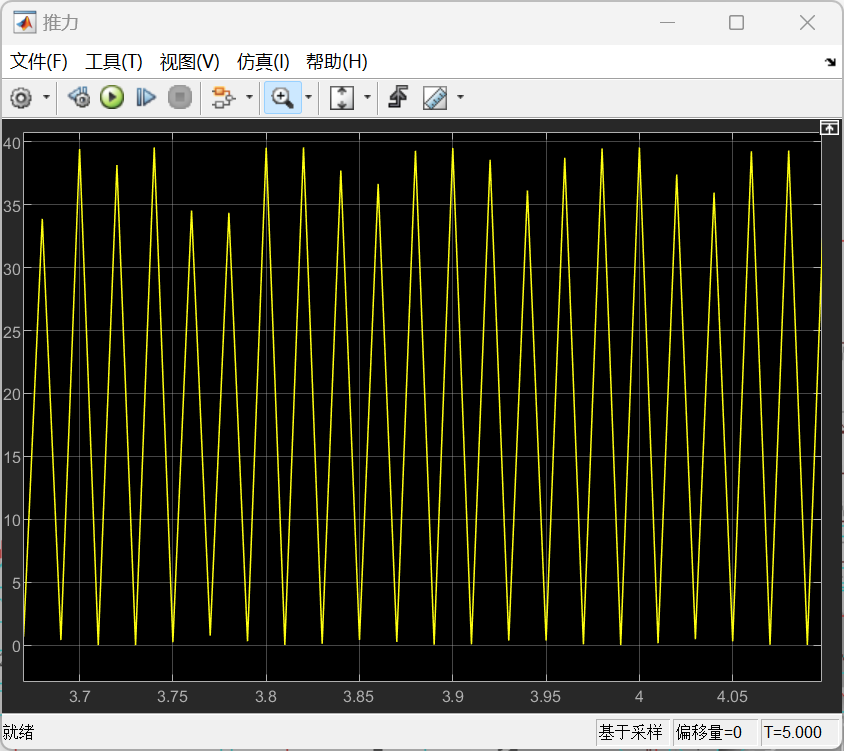
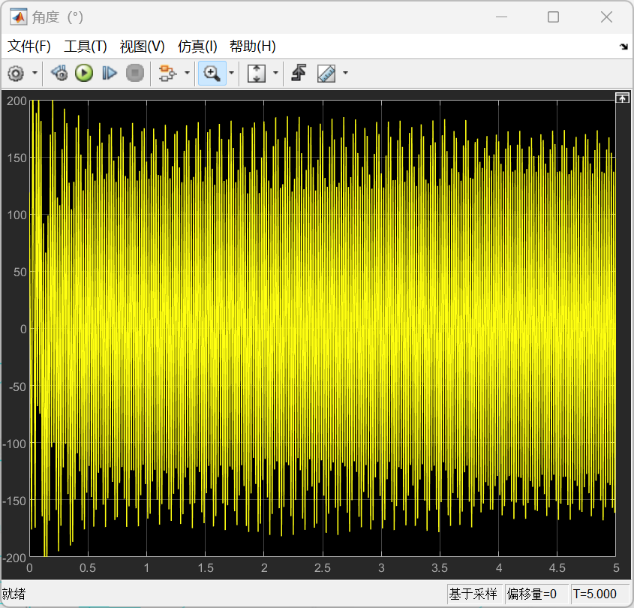
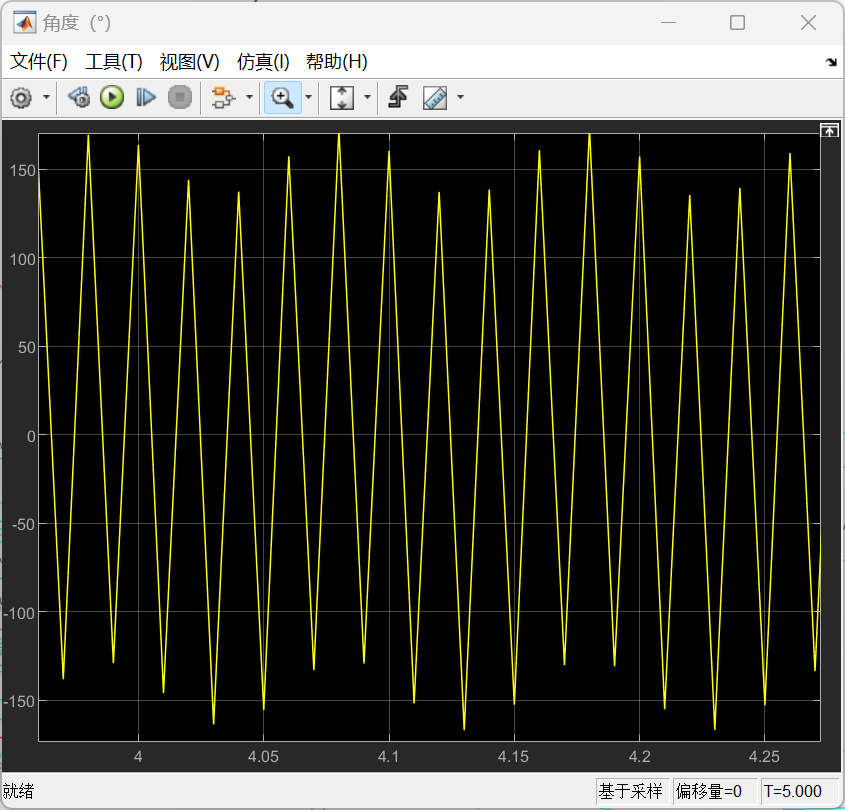
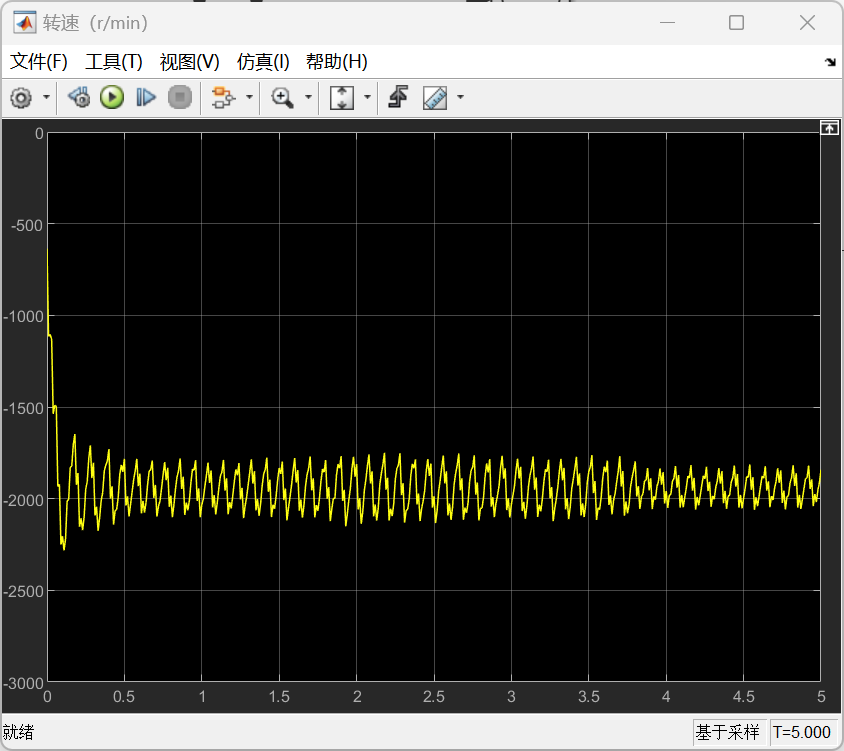
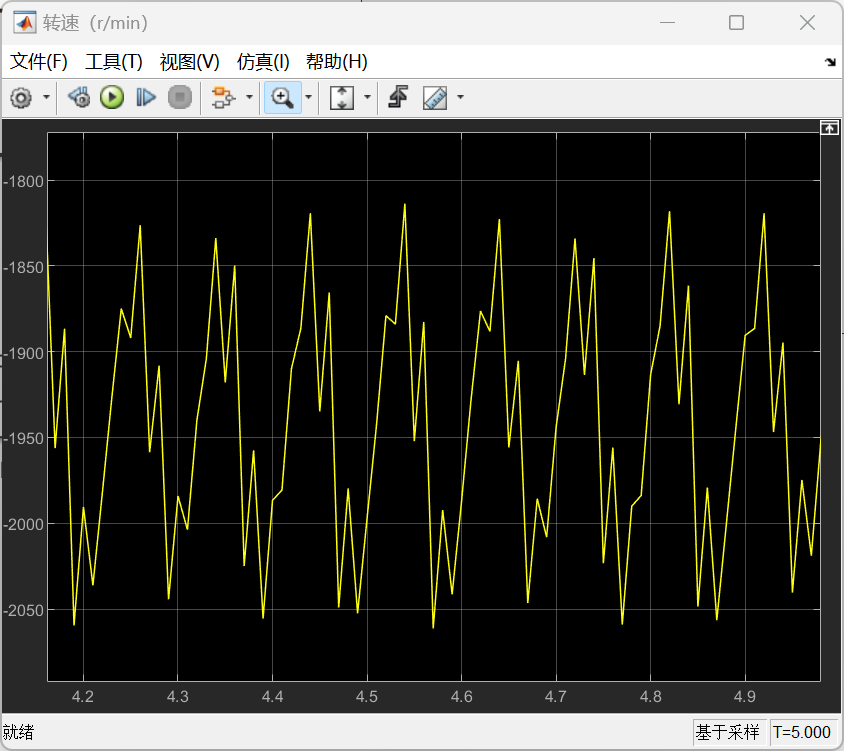
以上所有图像左图均为整体图像，右图均为局部图像。根据仿真结果可以看到，尽管大部分时候转速不是特别稳定，但是转速基本上能够满足功率输出的要求，同时也可以发现，在不加入减振措施的情况下，整体呈现出受到振动的扰动是很明显的，可以看到局部以及整体的一种周期性的输出变化。

4 中途迭代过程

4.1 设计产生的问题

对于β型来说，存在的最大问题是，尽管气缸最后的密封性设计加工得没有问题，达到按下做工活塞，配气活塞能够弹出的水准，但是在加热测试时，可以感受到气体推动气缸向外运动，但是向内移动时阻力没有明显增大，再次往外时活塞依然能够被推动，但是最终无法完整自行运转，分析情况如下：这是由于没有回热器导致的，冷热腔内的气体不能快速交换，这使得气体做工后不能快速进入冷腔内推动配气活塞转动，在回转时也无法快速由配气活塞压回，这使得斯特林循环中的加热和冷却两部分需要消耗的时间大大增加，也是造成β型的pv图像比较奇怪的原因，而α型采用了回热器的设计，就不存在相同的问题。

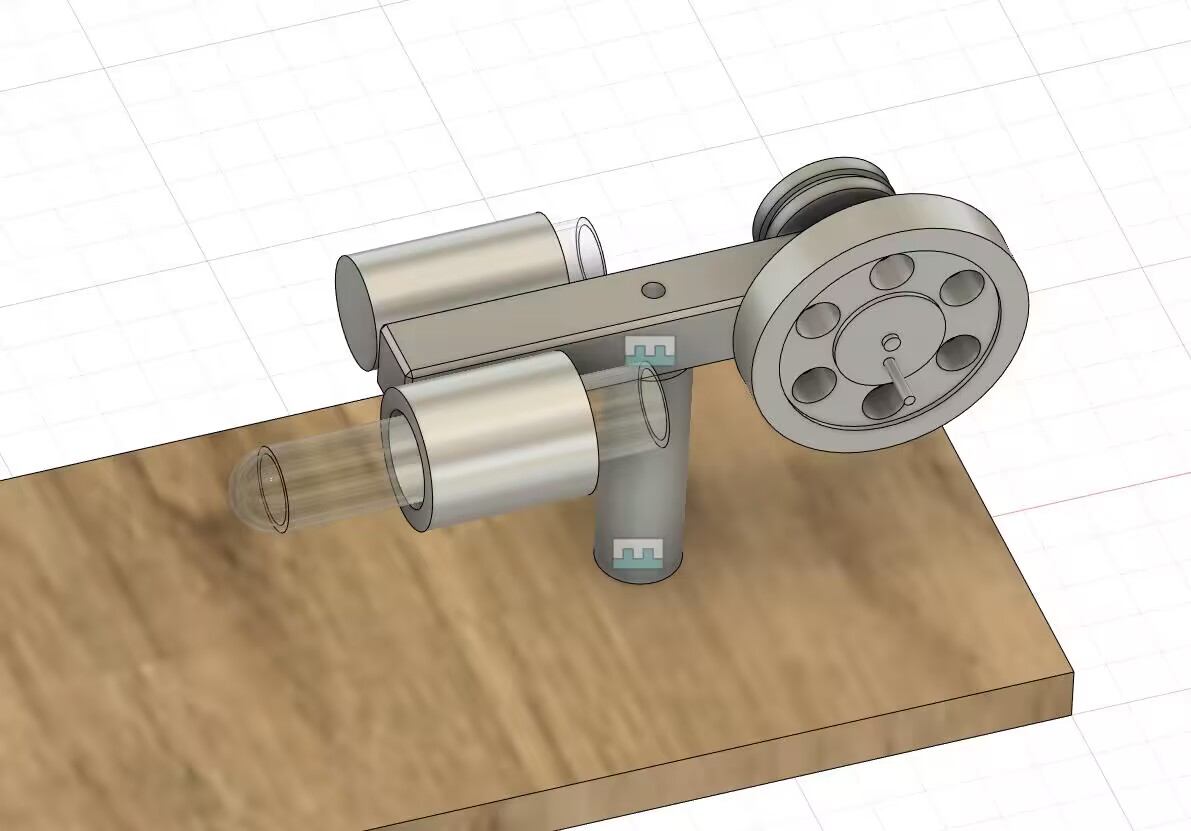
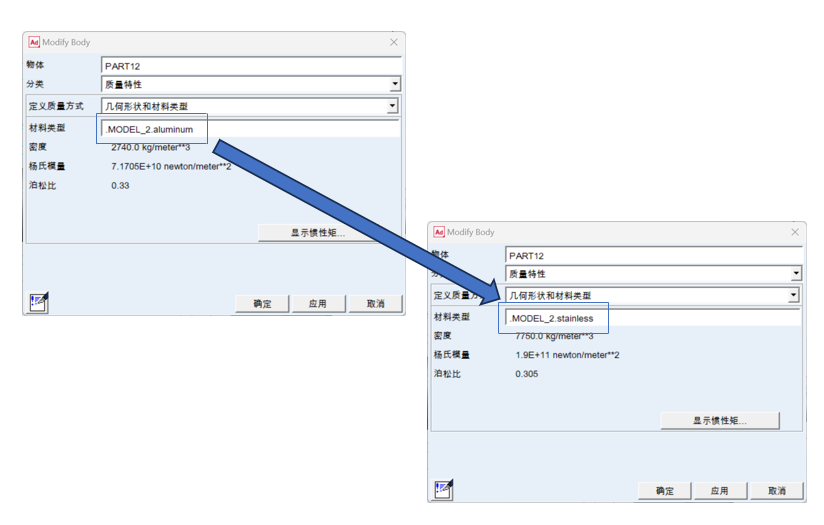
对于两种发动机来说，共有的问题是缸体与活塞的配合，采用金属加工的气缸时，常常出现配合不好的问题，需要经过手动打磨进行调整，从而使其能够进入，但是这样的话往往会导致后续的气密性测试出现不可控的问题，而且即使跟厂家要求加工后气密性测试达标之后再发货，到手测试也不一定能够完全达标，我们在最大限度采用金属气缸的情况下，采购了配套出售的玻璃气缸和活塞作为确保能够达到运行要求的方案，最终在α型的设计和测试中成功完成了尽可能多采用自己设计的金属气缸的同时能够确保发动机能够正常运行。

4.2 仿真部分的调整

在12月5号课程的汇报中，老师对于我们的仿真提出了一些指导意见，其中最主要的就是提到将气体对活塞推力转化为飞轮转矩的合理性，以及随之带来的传动过程中的摩擦问题。同时老师还提到，不要轻易的去改动原先设计的尺寸参数，事实上在第一阶段的改动中仅仅是在热力学计算以及对应推力与转矩计算中改动了对应的参数，而由于修改模型再重新导入Adams设置连接与参数过于麻烦所以并未对应进行调整，所以我们对气缸与活塞半径的修改进行了回退处理。

事实上，基于斯特林发动机整体的运作机理考虑，首先需要在预热的同时人为拨动飞轮，本质上与给予初始转矩相对应，因此在t<0.1s的启动阶段，仍然保留了初始力矩值torque的设定，而在后续的循环运作阶段传出实时气体对活塞的推力Fp作为force的值。

经过对于各种参数的多次调整与运行，我们进行了如下的补充仿真（该过程主要在β的仿真完成，因此下述所有内容均在β型发动机的基础上完成，α型发动机的相关仿真已经过了同样的仿真优化步骤，结果是准确的）：

（1）给定初始力矩对于转速的影响

我们分别设定t<0.1s时给定的初始转矩Torque=-0.5和-0.05，运行仿真并得出转矩图线：

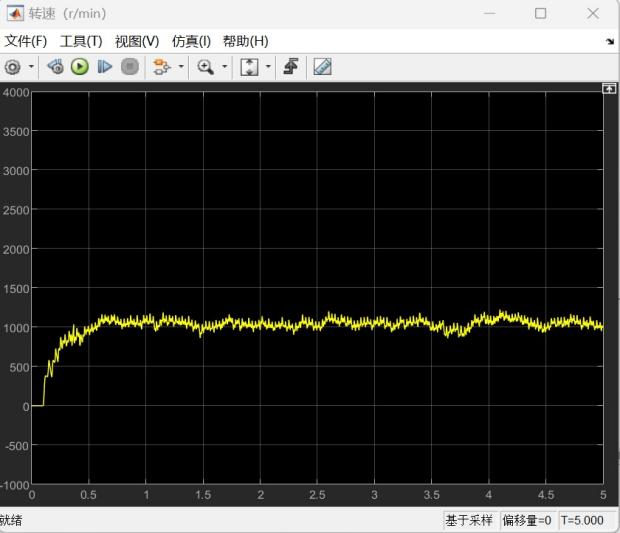
通过观察上述两图并对比可以发现，事实上初始转矩的大小是决定运行初期转速变化情况的主要因素，具体体现为若初始转矩较大则会出现转速突增现象而降低初始转矩后则该现象消失，同时初始转矩较低时稳定后的转速也有对应降低，但降低幅度有限，大致还是稳定在1200rpm左右；同时在取消转换为传动后力矩这一操作后，转速也较之前有了明显的降低，说明各部件之间连接在动力学实际运作过程中的影响不可忽略，主要是由于各传动部件存在质量且相互的配合之间会产生摩擦。

（2）反转带来的反思——改变初始力矩方向（符号）

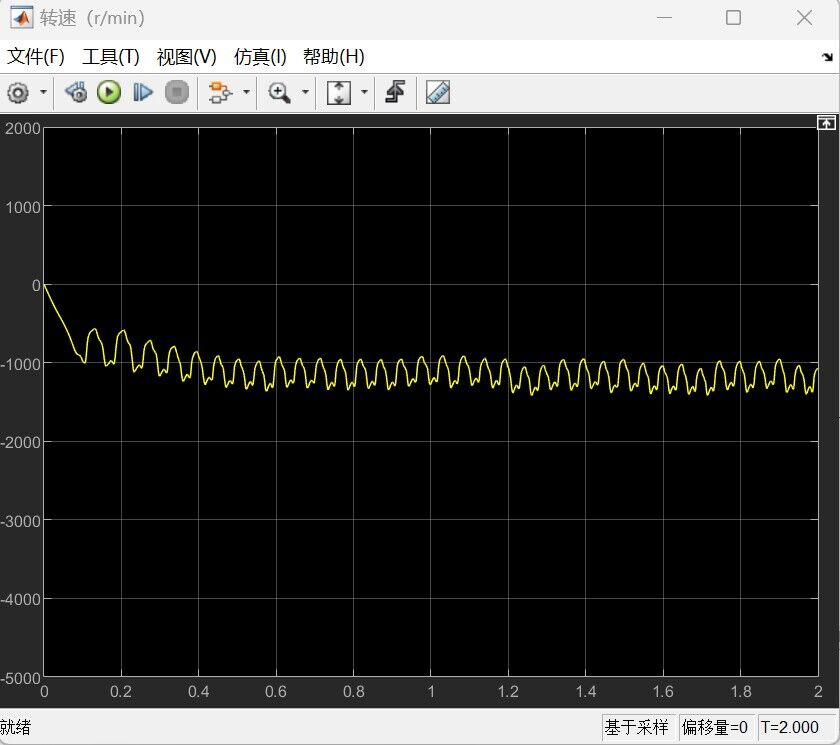
根据上述图线，我们发现在0.1s初始力矩作用后正向转速达到最大值，此后却一直衰减直至反向，而飞轮反向旋转后转速却一直增大，且在5s仿真末尾阶段有逐渐平稳的趋势。因此，我们考虑将初始力矩的符号改变（即方向更改）观察仿真效果如下（设置torque=0.05)：

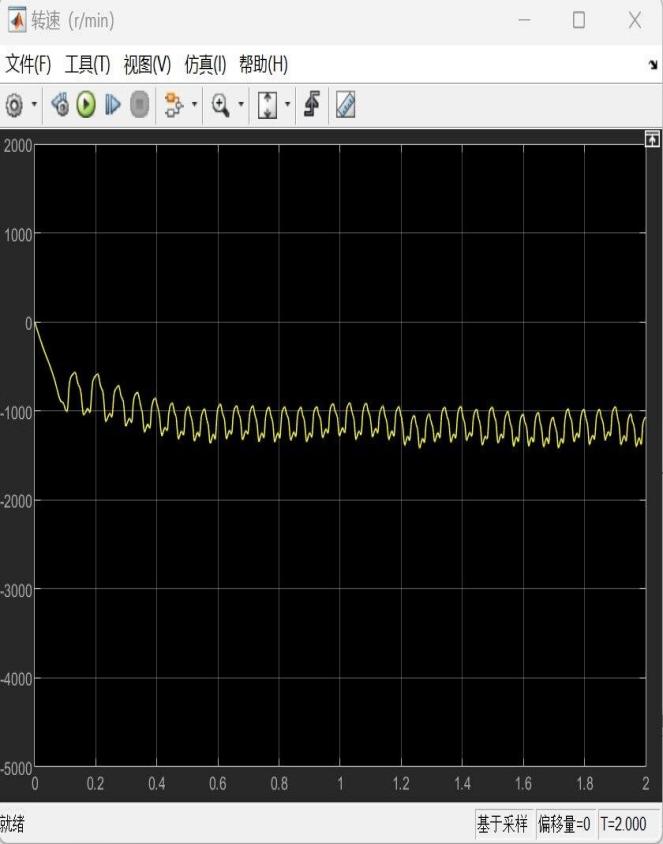
可以发现，在初始力矩反向之后，转速的方向也随之改变，且在初始力矩施加的0.1s后迅速趋于平稳，稳定后转速平均值在1100rpm左右，仍然大于热力学计算中理论所需的最低转速573.6rpm，满足设计要求。

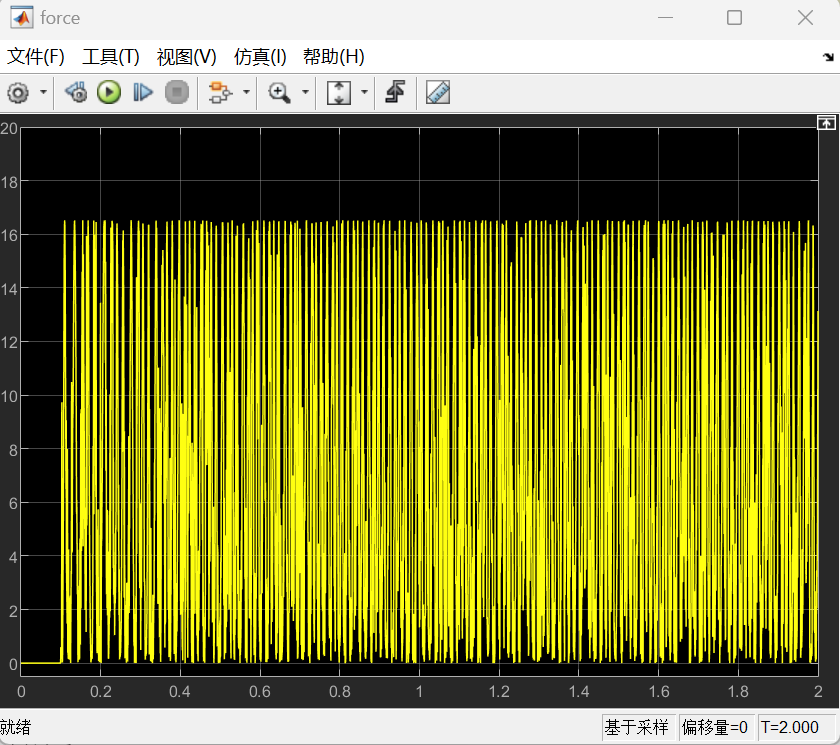
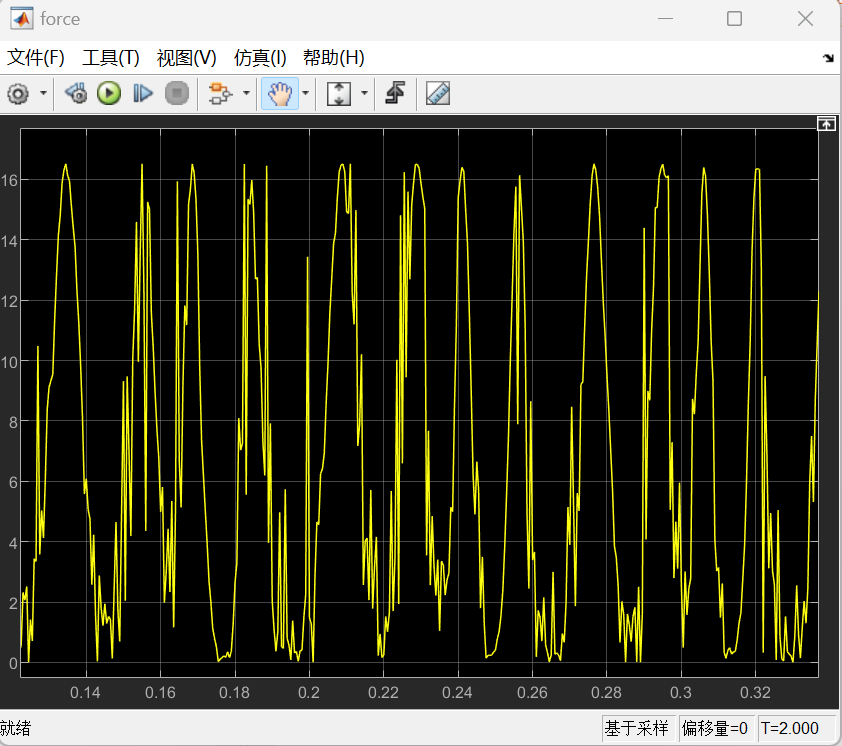
该情况下对应的推力force与转角theta图线如下图所示：

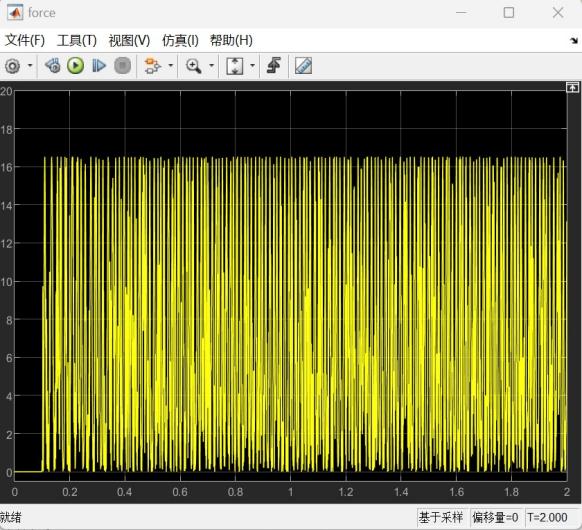
经过调整之后的仿真结果排除了摩擦设置不准确，振动与实际不符，转速波动过大等问题，使得结果更加准确，在后续采用玻璃气缸时提供了可靠参考。

4.3 最终调整

该部分主要介绍自从α在不带电机能够转动之后的一些调整，以及在最终测试前发现的一些问题，以及剩余时间中对于未能成功运转的β型进行的调整。

首先是对于玻璃气缸的连接的润滑作出的一些调整，我们一开始采用矿物油进行润滑，希望既能够起到润滑作用，又能减少气体外溢，提高密封性，但经过实际测试的结果来看，效果是很不好的，反而减慢了达到稳定转动时的转速。跟气缸商家进行交流后，商家建议使用石墨进行润滑，因为油的粘性和表面张力很大，再加上玻璃活塞的粗糙表面，会增加很多摩擦力，采用石墨虽然不一定能增强其气密性，但是润滑效果要好的多半，经过实际测试之后，效果有很大提升。

其次是电机带动产生的问题，一开始我们购买的电机功率较大，产生的电磁阻力矩也比较大，在使用橡皮圈进行带动时，未能成功使其按照设想转动，稍微有点阻力就会停下，灯泡也不能按照预想的情况发光。后来，经过加热位置调整，更换电机，减少橡皮筋的张力等方法，我们成功地减少了整体的阻力，还成功地消除了橡皮筋相对于主从动轮之间的滑动，提高了功率输出效率，更换更大的从动轮，减少阻力矩，最后成功地使了功率为5w的灯泡发亮（实际功率大约在3w左右，没有达到灯泡最亮的情况），实际观察稳定转速在2300r/min左右，比仿真的转速要高一些，且实际做功冲程的长度和温度要略高一些，总体评估下来还是符合计算结果的，此外，我们发现，加负载后，需要更大的初始推动力，甚至需要推动两次，才能使其稳定旋转，估计是单次做功冲程提供的机械功较少导致，不过最后不影响实际运行的效果，达到稳定后无需人为干预。

对于β型，我们对于不同公差的气缸玻璃外套对现有的金属气缸进行测试，找寻气密性和推动效果的组合，实际上受阻还是比较大，因为每次都需要经历粘胶解胶的漫长过程，中途还需要手动打磨等，较大的零件调整时间上也不是很充裕。较长时间的加热有时候也会导致打印支架的部分融化导致损坏。不过我们经过调整，还是找出了一个目前能够实现最好推动和气密性的气缸，虽然依然不能正常带动斯特林发动机做功，不过相比于其他的组合，加热时可以感受到明显的外推力，压缩时也不会出现阻力过大的情况。

最后是0.5w功率的表征，我们采购到了由十个5730灯珠串联得到的灯泡，在发动机稳定旋转带动发电机时，测定灯泡的电压，最终完成对0.5w功率的表征。

5730灯珠的参数如下：

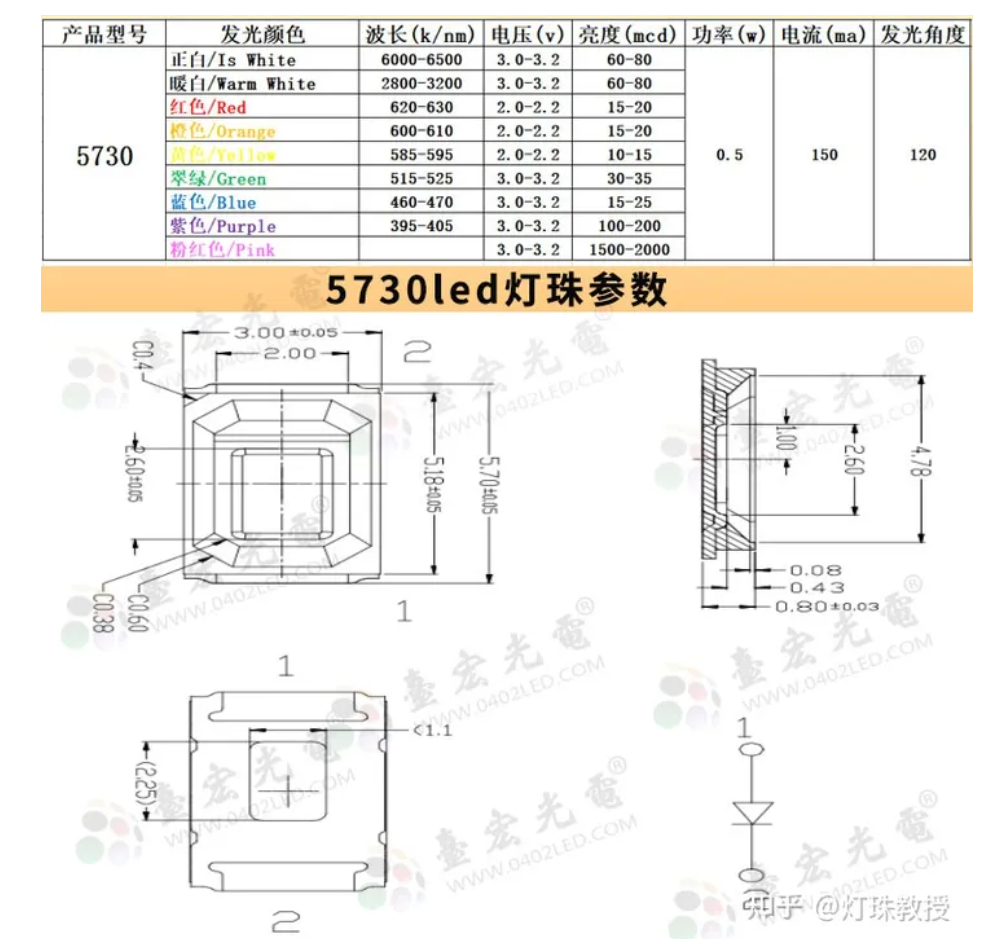
灯泡内部结构和实际电压测量情况如下：

则可以得到，能使串联的灯泡发亮，则需要电流1.5A,电压3.4V,则计算功率得到5.1W，虽然实际电流可能没达到1.5A，功率可能小于5W，但是对于0.5W的要求来说，已经足以满足转速的测试，满足了测试的范围要求。

最后测试时得到空载电压3.91V，负载电流19mA，则最终计算得到输出在电机上的功率为0.074W，没能完全达到0.5W的要求。

5 反思与总结

尽管经过计算验证，输出到飞轮上的功率是超过0.5W的，但在使用电机进行实际测试时，还是没有达到预想的地步，一有可能是皮带，电机等设计效率降低比较大，损耗了很多能量，另一个是测试时不能很好确保稳定旋转，存在一定的测量误差，但纵观整个过程，实现效果还是相对成功的，只有0.5W的指标没有完成。

对于机械结构和公差配合的设计，我们有了很大的了解，尤其是在气缸的密封性以及最终成功运作上，不一定没有误差就能够保证气缸能够按照预想的方式正常运行；振动的产生和各器件的使用寿命的匹配的相关设计和思考在经过学习之后有了系统性的思考模式和设计方法；对于传动结构的受力分析和功率计算也在经过锻炼后有了更多更快更加准确的方法。

仿真软件在热力学部分和机械运动部分的运用使我们明白了如何通过仿真结果调整设计，以及根据实际测试情况调整仿真出现的问题从而更好地适配制作好地成品，此外，对于仿真软件的运用也提高了对于机械结构的认知以及建模装配等等方面的一些技术应用。

在实际调整中一些零件和工具的使用也使得我们的实践经验有很大提高，能够进行简单的加工，以及在设计思考加工方式从而减少加工难度和降低加工成本，提高迭代速度和优化方法；此外，在装配过程中，协作进行操作和调整也使得我们对于各种构件的装配和使用有了更加深入的了解。

一、初始设计参数与热力学计算

对于我们设计的β型斯特林发动机，提出了如下的设计目标：

在我们初步设计的斯特林发动机（模型如下图所示）中，相关的尺寸参数如下：

将设计好的模型导入Ansys软件中进行静态热力学的仿真（如下图所示），可以得到气体温度的状态参数如下：

根据史密特理论的相关计算公式，可以编写相应程序，由以上参数为基础计算并绘制P-V图以及单次循环所作功，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

afa=2*85*pi/360;
theta=0:0.01:pi*2;
tc=439;
te=611;
l1=0.021;
h1=l1*2;
l2=0.0225;
h2=l2*2;
r=0.01;
r0=0.008;
vse=r0*r0*pi*h1;
vsc=r*r*pi*h2;
ve=vse.*(1-cos(theta))./2;
vb=(vse+vsc)./2-sqrt((vse.*vse+vsc.*vsc)./4-vse.*vsc.*cos(afa)./2);
vc=vse.*(1+cos(theta))./2+vsc.*(1-cos(theta-afa))./2-vb;
vr=(r*r-r0*r0)*0.02*pi;
tao=tc/te;
k=vsc/te;
xb=vb/vse;
x=vr/vse;
fai=atan(k.*sin(afa)./(1-tao-k.*cos(afa)));
s=tao+4.*tao.*x./(1+tao)+k+1-2.*xb;
b=sqrt(tao.*tao+2.*k.*(tao-1).*cos(afa)+k.*k-2.*tao+1);
deta=b./s;
pmin=101300;
p=pmin.*(1+deta)./(1-deta.*cos(theta-fai));
plot(rad2deg(theta),p);
xlabel('角度θ（°）');
ylabel('压强P（Pa）');
title('α=85°时θ-P图线');
v=ve+vr+vc;
figure;
plot(rad2deg(theta),v);
xlabel('角度θ（°）');
ylabel('体积V（m^3）');
title('α=85°时θ-V图线');
figure;
plot(v,p);
xlabel('体积V（m^3）');
ylabel('压强P（Pa）');
title('α=85°时P-V图线');
w=10000000*pmin.*vse.*pi.*deta.*(1-tao).*sin(fai).*sqrt(1-deta)./((1+sqrt(1-deta.*deta)).*sqrt(1+deta));
disp(w);

通过运行上述代码，可绘制出如下热力学数据图线，并计算出单次循环做功为**0.0523J**。

因此，若要达到设计目标的0.5W功率要求，需要转速达到rmin=0.5*60/0.0523≈573.6rpm。

此外，以上设计参数所得到的P-V图线偏扁圆形，与常见的P-V图线形状有一定差异，这主要是与设定的初始相位角有关，若将相位角改为45°，则可以得出如下P-V图线，并可计算得出此时对应的单次循环做功为0.0608J，较先前有所提高；但在β型斯特林发动机中，相位角是由相关零件的设计直接确定的，故在后面的仿真中仍然保持相位角α=85°的设定。

二、Adams动力学仿真

在不考虑各类摩擦的情况下，对于基本的曲柄连杆传动机构来说，有如下基本公式：

根据此公式可得到如下代码，绘制转矩变化曲线如下图：

1
2
3
4
5
6
7
8
9
10

ap=pi*l2*l2;
   fp=ap.*(p-pmin);
   tq=(sin(theta)-cos(theta)).*fp.*r;
   t_qm=w/2/pi;
   t_qm_(1,1:629)=t_qm;
   figure;
   plot(rad2deg(theta),tq,rad2deg(theta),t_qm_);
   xlabel('角度θ（°）');
   ylabel('转矩');
   title('转矩变化曲线');

根据如下仿真步骤，将Fusion360建模软件中建立完成的模型导出为STEP格式，进入Adams仿真软件中进行进一步的动力学仿真。

在第一次仿真时，仅仅将原有模型中设计到传动的部分保留，并将简化后的模型导入仿真，主要反映出两大问题，第一时间进行了修改（以上给的参数均为该次修改后确定的）：

（1）传动部分设计失误，主要表现为各个曲柄的转动不同轴而导致角速度不一致，从而无法达到稳定的压缩与膨胀之间的状态转换，即活塞体系无法完成循环；

（2）连杆设计尺寸不合适，导致部件之间出现穿模问题。

通过修改转动轴连接方式，重新捋清传动循环原理并对不合适的尺寸进行修改（将连接排气活塞的连杆长度缩短），最终实现了在给定初始转速下动力学仿真模型的稳定运转（演示效果见PPT）。

在验证Adams模型与连接建立设置的可行性后，为进行下一步仿真，设置了系统单元变量（推力，对应的力矩，飞轮转动角度与角速度），并将前两者作为输入，后两者作为输出，利用Controls插件导出对应文件以供与MATLAB中Simulink的联合仿真。

三、Simulink联合仿真

打开Adams导出的m文件并运行从而加载对应系统变量，在命令行中输入adams_sys指令即可进入Simulink仿真界面。根据计算与仿真需求，建立Simulink原理图如下：

通过上述分析可知，对于整个发动机来说，我们需要根据不同时刻气缸中密封气体的状态来计算其对活塞的推力，并将其转换为转矩施加在飞轮上，从而形成对整个发动机循环工作的驱动。因此，在Adams建立系统单元时，我们选择气体推力及其等效飞轮转矩（无摩擦情况下）作为整个系统的输入变量，而将飞轮转动的实时角度作为输出量，同时设置飞轮转动的角速度即转速作为最终需要监测的关键输出变量。其中，气体对活塞产生的推力本质上与飞轮转动的实时角度息息相关，也正因此需要将该角度作为Adams仿真系统中的输出变量，以便于在Simulink中回传至模型中进行迭代仿真。而实现角度信息到推力乃至转矩数据的转换，就需要在Simulink中插入S-Function进行实时计算处理。在本原理图中，左侧的plant框体即为我们设置的S-Function函数。

事实上，计算推力乃至转矩关键就要计算气缸内密封气体对于活塞产生的压强，也就是气压值P，而这一值在前面的热力学分析中已有提及，并有相应的公式可以根据实时的飞轮转动角度给出对应气压P的计算。于是，通过对于上述热力学斯特林循环代码的简单改写，结合推力与转矩的转换，可以得到plant函数代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

function [sys,x0,str,ts,simStateCompliance] = plant(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1; 
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [0 0];
simStateCompliance = 'UnknownSimState';
end

function sys=mdlDerivatives(t,x,u)
sys = [];
end
function sys=mdlUpdate(t,x,u)
sys = [];
end
function sys=mdlOutputs(t,x,u)
theta=u;
afa=2*85*pi/360;
tc=439;
te=611;
h1=0.042;
h2=0.045;
r=0.01;
r0=0.008;
vse=r0*r0*pi*h1;
vsc=r*r*pi*h2;
vb=(vse+vsc)./2-sqrt((vse.*vse+vsc.*vsc)./4-vse.*vsc.*cos(afa)./2);
vr=(r*r-r0*r0)*0.02*pi;
tao=tc/te;
k=vsc/te;
xb=vb/vse;
x1=vr/vse;
fai=atan(k.*sin(afa)./(1-tao-k.*cos(afa)));
s=tao+4.*tao.*x1./(1+tao)+k+1-2.*xb;
b=sqrt(tao.*tao+2.*k.*(tao-1).*cos(afa)+k.*k-2.*tao+1);
deta=b./s;
pmin=101300;
P=pmin.*(1+deta)./(1-deta.*cos(theta-fai));
Ap=pi*r*r;
Fp=Ap.*(P-pmin);
%对曲柄转矩 N.m
if t<0.1
force=0;
torque=-0.4;
else
Tq=(sin(theta)-cos(theta)).*Fp*r;
force=0;
torque=Tq;
end
sys(1)=force;
sys(2)=torque;
end

function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
end
function sys=mdlTerminate(t,x,u)
sys = [];
% end mdlTerminate
end

除此之外，由于两个仿真系统之间的运算单位不统一，在将Adams中角度单位改为rad（弧度），长度单位改为m后，仍然需要对相应的角度与转速数据进行单位上的换算处理（如下图所示），从而可以得到数量级正确的数据图线。

经过以上处理，并将adams_sub单元中的仿真模式（改为interactive）与步长（根据情况改为0.0001或0.0005较为合适）进行对应调整后，可以得到仿真结果的数据波形图如下（仿真时间设置为5s)：

**图线结果分析**：

（1）转速开始突增的原因：初始转矩设置为0.4（负方向），相对于后续整体产生的转矩值都较大，因此在开始时转速在迅速增长后又回落；

（2）可以看到转速在短暂突增后逐渐趋于平稳，但稳定在3000rpm左右，这个转速较快，在现实中可能较难实现，会超过实际材料的承受极限；

（3）但转速在稳定后仍有较大波动，初步判定是由于飞轮质量较轻导致其转动产生的震荡较大，初步观察图线可以发现其在平均值附近最大有将近±300rpm的浮动，需要在后续处理中予以优化；

（4）角度的变化较为规律，且在单位换算调整后能够基本稳定在-180°到180°之间（偶尔有小的浮动），说明仿真运行基本正常；

（5）转矩的变换也与前面动力学分析时绘制的转矩图线基本吻合，随角度变化也呈周期性变化，符合理想情况。

四、迭代改进及其仿真

在上述章节中，我们已经完成了从Adams力学建模仿真到接入Simulink建立联合仿真并得到转速变化图线结果的全过程，但仍然存在一些问题，需要进行进一步修改以达到预期效果并指导发动机对应尺寸的设计修改。

1.初次修改——调节设计参数

在之前的初步仿真中，得出的转速会在短暂突增后稳定在3000rpm左右，这在实际中对于我们设计的结构规模来说是不太可能实现的，同时也远远超出了实际材料的结构强度与承受范围，因此为了将稳定时的转速降低，同时进行了如下两处改动以达到效果：

（1）减小活塞与气缸半径

减小活塞与气缸半径实质上是减小了活塞受气体推力作用的横截面积，同时也减小了气缸中容纳的气体体积，但由于密封前仍与外界空气联通，故初始气压（即Pmin）仍与大气压一致，也因此该改动实际上是降低了相同温度状态下气体的压强，从而导致气体对活塞推力的减小，传动到飞轮上的转矩也随之减小，最终导致了转速的降低。

在本次改动中，我们对活塞与气缸半径均进行了减小处理，并在plant函数中对应的结构参数部分做出了对应的调整，调整后的参数如下表所示：

该设计参数的调节也同步影响到了单次循环做功的数值，通过重新代入修改后的参数进行热力学参数的计算，得到此参数下单次斯特林循环的做功数值为**0.0327J**。

（2）增大飞轮质量（转动惯量）

在之前的仿真中为便于贴合加工处理将所有部件的材质设置为铝（密度较低，质量轻），但是结果显示转速在大致稳定后仍然出现了一定程度的震荡浮动，这是我们想要避免的。因此，一方面为了降低转速的浮动幅度，另一方面也是为了通过增加转动惯量加大负载从而降低转速，我们希望将飞轮的质量增大；同时，为了尽可能减少我们的修正对于整体建模结构的影响，我们尽量不去改动飞轮本身的尺寸，而是在Adams中对于飞轮部件的质量特性做出调整，通过将其材质由铝转换为密度更大的不锈钢从而实现增加飞轮质量的效果。

综合以上两点调整后，再次进入Simulink中运行仿真，同时由于调整结构设计参数降低了气体对活塞做功施加到飞轮上的等效转矩的整体数值，因此也将初始驱动力矩降低为-0.2（尽可能贴近气体膨胀压缩产生等效力矩的浮动范围）以尽可能降低初始力矩对于最终稳定转速的影响，得到仿真结果如下图（演示视频见PPT）：

**图线结果分析**：

（1）转速在仿真开始阶段的突增消失；

（2）转速在短暂的增加后迅速达到平稳状态，且稳定在1450rpm左右，较先前有了明显的降低，同时结合更改参数后热力学计算得到的单次斯特林循环做功数值为0.0327J，可以得出此时斯特林发动机运行的理论功率为0.7906W，满足初始设定的设计要求；

（3）但转速在稳定后的波动明显减小，观察图线可以发现其在平均值附近仅有±50rpm左右的浮动，运行基本处于稳定状态；

（4）角度的变化较为规律，且在单位换算调整后能够基本稳定在-180°到180°之间（偶尔有小的浮动），说明仿真运行基本正常；

（5）转矩的变换也与前面动力学分析时绘制的转矩图线基本吻合，随角度变化也呈周期性变化，符合理想情况。

2.汇报后的更正——活塞推力的给予方式改变以及传动机构间摩擦的添加

在12月5号课程的汇报中，老师对于我们的仿真提出了一些指导意见，其中最主要的就是提到将气体对活塞推力转化为飞轮转矩的合理性，以及随之带来的传动过程中的摩擦问题。同时老师还提到，不要轻易的去改动原先设计的尺寸参数，事实上在第一阶段的改动中仅仅是在热力学计算以及对应推力与转矩计算中改动了对应的参数，而由于修改模型再重新导入Adams设置连接与参数过于麻烦所以并未对应进行调整，所以我们对于气缸与活塞半径的修改进行了回退处理。

事实上，基于斯特林发动机整体的运作机理考虑，首先需要在预热的同时人为拨动飞轮，本质上与给予初始转矩相对应，因此在t<0.1s的启动阶段，仍然保留了初始力矩值torque的设定，而在后续的循环运作阶段传出实时气体对活塞的推力Fp作为force的值，因此改动plant函数对应部分如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

pmin=101300;
P=pmin.*(1+deta)./(1-deta.*cos(theta-fai));
Ap=pi*r*r;
Fp=Ap.*(P-pmin);
if t<0.1
force=0;
torque=-0.4;
else
force=Fp;
torque=0;
end
sys(1)=force;
sys(2)=torque;
end

同时为监测对应的推力改变情况，修改Simulink系统原理图如下：

经过对于各种参数的多次调整与运行，我们进行了如下的补充仿真：

（1）给定初始力矩对于转速的影响

我们分别设定t<0.1s时给定的初始转矩Torque=-0.5和-0.05，运行仿真并得出转矩图线：

通过观察上述两图并对比可以发现，事实上初始转矩的大小是决定运行初期转速变化情况的主要因素，具体体现为若初始转矩较大则会出现转速突增现象而降低初始转矩后则该现象消失，同时初始转矩较低时稳定后的转速也有对应降低，但降低幅度有限，大致还是稳定在1200rpm左右；同时在取消转换为传动后力矩这一操作后，转速也较之前有了明显的降低，说明各部件之间连接在动力学实际运作过程中的影响不可忽略，主要是由于各传动部件存在质量且相互的配合之间会产生摩擦。

（2）增加飞轮与支架在旋转时产生的摩擦

综合各因素的调整与尝试，发现在各部件的传动摩擦中只有飞轮与支架之间由于飞轮旋转而产生的摩擦对于整体装置运作的影响相对较大，因此加上原本设置的气缸——做功活塞与做功活塞——排气活塞间摩擦（动摩擦系数均设置为0.5），运行Simulink仿真有如下结果：

观察图线可以发现，增加传动摩擦后，转速在短暂增长（由于初始转矩）后迅速衰减，并在0.34s左右停止转动。

为改变这一现象，计划采取润滑的方式降低动摩擦系数，因此在设置时将动摩擦系数降为0.2，重新运行Simulink仿真，转速图线结果如下：

观察图线可知，当摩擦系数降低后，转速衰减速率也明显降低，但仍有明显衰减且在2.5s左右发生反转现象，且转速逐渐增大。

（3）反转带来的反思——改变初始力矩方向（符号）

根据上述图线，我们发现在0.1s初始力矩作用后正向转速达到最大值，此后却一直衰减直至反向，而飞轮反向旋转后转速却一直增大，且在5s仿真末尾阶段有逐渐平稳的趋势。因此，我们考虑将初始力矩的符号改变（即方向更改）观察仿真效果如下（设置torque=0.05)：

可以发现，在初始力矩反向之后，转速的方向也随之改变，且在初始力矩施加的0.1s后迅速趋于平稳，稳定后转速平均值在**1100rpm左右，仍然大于热力学计算中理论所需的最低转速573.6rpm，满足设计要求**。

该情况下对应的推力force与转角theta图线如下图所示：

五、感悟与总结

通过完成本次动力学仿真，对于斯特林发动机的热力循环过程以及机械转动部分的运作过程有了更加细致和深刻的理解，同时也通过函数的编写与变量的选取对于定量计算中的细节有了更深刻的把握。特别是Adams仿真过程中在建立变量（系统单元）时对于角度和角速度测量的坐标系选取，非常考验对于体系运动过程中细节的把握，究竟是哪个点绕着哪个点转才是正确的角速度，只有正确选取才可能得到正确的结论；单位换算也是仿真过程中的一大难点，不仅要在Adams中对于默认的单位进行修改，还要在MATLAB中编写对应的函数完成转换（Simulink图中的MATLAB Function图标中的函数内容），才可以得到正确的数值结果。除此之外，整个仿真过程中由于涉及到两个软件的联动，对于电脑的性能与配置也有不小的要求（具体体现为把MATLAB和Adams都重装了至少三遍最后还是被迫在别人的电脑上完成，说来也神奇，同样的模型，同样的代码，传到别人电脑上就能跑，我的就不行）。

在完成了整套仿真的流程并得到了正确的数值与图线结果后，还需要针对我们所需要的性能，结合实际情况的可行性，对于对应参数进行修改。经过不断的尝试和摸索，目前有如下的初步结论：

（1）调大飞轮的质量（改变材质，增大材料密度而不改变原本飞轮的尺寸设计），可以使得转速在稳定后的周期性波动幅度明显减小；

（2）为贴近真实情况，应该直接采用气体膨胀压缩对活塞的推力作为输入变量进入Adams仿真系统中进行仿真，转速会比转换为等效转矩作用于飞轮上的更低（因为传动部件本身具有的质量不可忽略，且各部件间存在摩擦）；

（3）传动部分的摩擦损耗主要体现在飞轮在旋转过程中与支架的摩擦力；

（4）如果代入铝材间原有的摩擦系数，发动机无法正常工作，需要通过加润滑油等方式来实现摩擦系数的降低；

（5）初始力矩对应的是发动机在预热阶段用手拨动飞轮产生的驱动力，该转矩会直接影响飞轮在发动机工作初期的转速，并对后续的稳定转速产生一定的影响；因此给定的初始力矩要与后续气体推力对应的等效转矩浮动范围尽可能贴近，以免出现开始时转速突增的现象；

（6）改变气缸与活塞的设计尺寸也能显著改变稳定后的转速，但并不建议这么做，因为需要每次重新导入对应修改后尺寸参数的新模型进行Adams中连接的创立，同时对于加工方面频繁的尺寸修改也不是长久之计。

总而言之，装置的转速与气缸与活塞的尺寸、飞轮质量（转动惯量）、摩擦系数等多方面因素有关。这次的仿真也指导了我们在后续的设计与加工过程中进行进一步的改进，并为发动机整体功率是否满足设计要求从计算上给出了合理的科学依据。