研究背景及其意义
图像放大与旋转是数字图像处理中最基础的几何变换操作,其核心在于如何通过插值算法重建原始图像中不存在的像素信息。当对图像进行放大操作时,输出图像的像素网格会超出原始图像的采样范围,需要通过插值来填补这些新增像素点的颜色值;而在旋转操作中,即使保持图像尺寸不变,原始像素的整数坐标经过旋转变换后也会落在新图像的非整数位置,同样需要通过插值来重新确定每个输出像素的颜色值。
图像插值是利用原图像中的颜色值通过一定的方法计算出待插入像素点的颜色值的过程。对图像进行插值一般有两个步骤:首先定义一个图像插值公式,然后利用该插值公式计算待插入点的颜色值。常见的图像插值算法有双线性法、最近邻法、非均匀法、双三次卷积插值法、双立方法、Lagrange法、 样条插值法、 克里金(Krijing) 插值法等。这些插值方法通常定义一个插值数据点的隐式函数,再提取该函数的等值面作为图像插值方法,常用的插值核包括线性插值核、样条插值核等。
- 最近邻插值作为最简单的算法,直接将距离待插值点最近的已知像素值作为结果,虽然计算效率极高(时间复杂度O(1)),但会产生明显的块状伪影(“马赛克”)和锯齿形边缘;
- 双线性插值通过考虑2×2邻域内四个像素的加权平均,在计算成本(O(n))和视觉效果之间取得平衡,但仍会导致高频信息丢失和边缘模糊;
- 更高阶的双三次插值(使用4×4邻域)和样条插值虽然能提供更平滑的结果,但计算复杂度显著增加(O(n²)),且可能引入不必要的振铃效应。
现有算法的根本局限在于采用统一的插值核函数处理整幅图像,忽视了图像不同区域的特征差异。例如,在平坦区域使用复杂插值会造成计算资源浪费,而在纹理丰富区域使用简单插值又会导致细节损失。基于此,我们希望通过改良的四平面插值算法对图像的放大与旋转效果进行优化,根据图像局部特征自适应地选择不同的插值策略,以规避用同一个插值公式对所有像素进行插值存在的不足。
常用图像插值算法
课本在6.5节中提到,在插值节点数量较多时,为避免Runge振荡现象的发生,并不提倡用高次多项式进行插值,而宁可用低次多项式作分段插值。在图像处理这一特定的应用场景中,需要处理的图像尺寸规模往往较大,且同一行(列)的所有像素颜色值显然并不具有可以用一个多项式函数显式表达的规律,但相邻的像素点颜色值之间又存在一定的关联性,因此分段插值仅考虑局部特征的特性在这里能够良好地契合所需性能。根据对于待插入像素点周围已有的像素点信息的利用情况,这里列举了几种常见的图像插值算法:
- 最近邻法:仅利用待插值像素点转换至原图像坐标后距离其最近的一个像素点的颜色值,将其直接作为待插值像素点的颜色值
- 双线性法:利用待插值像素点转换至原图像坐标后距离其最近的四个像素点的颜色值,加权平均后作为待插值像素点的颜色值
- 双立方法:利用待插值像素点转换至原图像坐标后距离其最近的十六个像素点的颜色值,加权平均后作为待插值像素点的颜色值
最近邻法
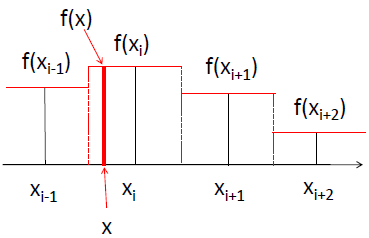
如上图所示,在一维最近邻插值中,坐标轴上各点 xi-1,xi,xi+1 … 两两对半等分间隔 (红色虚线划分),从而非边界的各坐标点都有一个等宽的邻域,并根据每个坐标点的值构成一个类似分段函数的函数约束,从而使各插值坐标点的值等同于所在邻域原坐标点的值。例如,插值点 x 坐落于 坐标点 xi 的邻域,那么其值 f(x) 就等于 f(xi)。
在二维的图像插值场景中,可以对上述一维最近邻插值进行推广,如下图所示:
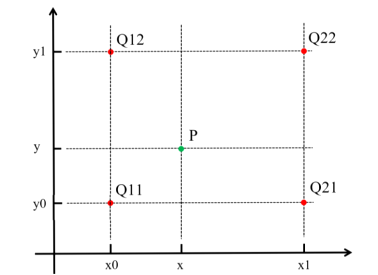
可以看到,(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) 都是原图像上的坐标点,颜色值分别对应为 Q11、Q12、Q21、Q22。而颜色值未知的插值点 (x, y)(需转换至原图像坐标),根据最近邻插值方法的约束,其与坐标点 (x0, y0) 位置最接近 (即位于 (x0, y0) 的邻域内),故插值点 (x, y) 的颜色值 P = Q11。
总而言之,最近邻法的基本思想即:将待插入点的坐标进行四舍五入,再以该行列坐标都是整数点的颜色值(灰度值)替代待插入点(x, y)处的颜色值。事实上,这也正是机器学习中KNN(K-Nearest Neighbor)算法在K=1时的情形。
基于以上算法思想,编写python函数代码实现图像放缩与旋转过程中的最近邻法插值:
1 | # 最近邻法插值实现图像放缩 |
双线性法
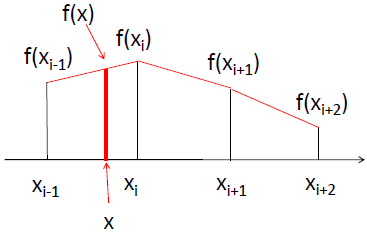
如上图所示,在一维的线性插值中,坐标轴上各点 xi-1,xi,xi+1 … 的值“两两直接相连”为线段,从而构成了一条连续的约束函数。而插值坐标点例如 x,根据约束函数其值应为 f(x)。因为每两个坐标点之间的约束函数曲线是一次线性的线段,对插值结果而言是“线性” 的,所以该方法称为线性插值。基于线性函数的特性,可以便捷地求取原图像上的两个像素点间任一待插值点的颜色值:
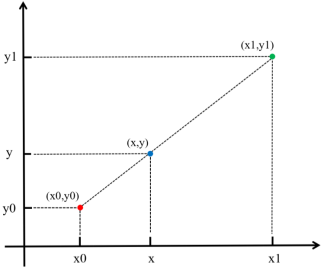
可以看到,图中 x0 和 x1 都是原有的坐标点,颜色值分别对应为 y0 和 y1,此时根据线性插值法约束,在 (x0, y0) 和 (x1, y1) 构成的一次函数上,颜色值未知的插值点 x的颜色值 y 即为:
$$
y=y_0+(x-x_0)\frac{y_1-y_0}{x_1-x_0}=y_0+\frac{(x-x_0)y_1-(x-x_0)y_0}{x_1-x_0}
$$
实际上,即便 x 不在 x0 与 x1 之间,该公式也成立(此时为线性外插),但图像处理中不需涉及此情形。
从一维的线性插值出发,很容易拓展到二维图像的双线性插值,通过三次一阶线性插值(本质为加权求和)获得最终结果,下图便展示了该过程的定性斜视与定量俯视示意图:
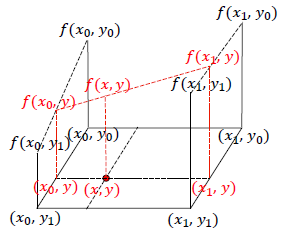
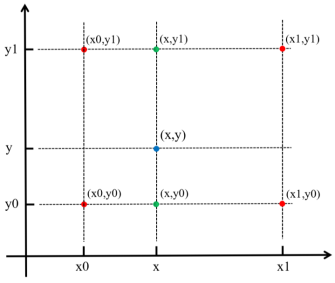
其中,(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) 均为原图像上的像素坐标点,颜色值分别对应为 f(x0, y0)、f(x0, y1)、f(x1, y0)、f(x1, y1)。而颜色值未知的插值点 (x, y),根据双线性插值法的约束,可以先由像素坐标点 (x0, y0) 和 (x0, y1) 在 y 轴向作一维线性插值得到 f(x0, y)、由像素坐标点 (x1, y0) 和 (x1, y1) 在 y 轴向作一维线性插值得到 f(x1, y),然后再由 (x0, y) 和 (x1, y) 在 x 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y)。
事实上,一维线性插值先作 x 轴向再作 y 轴向,得到的结果完全相同,仅为顺序先后的区别。这里不妨先由像素坐标点 (x0, y0) 和 (x1, y0) 在 x 轴向作一维线性插值得到 f(x, y0)、由像素坐标点 (x0, y1) 和 (x1, y1) 在 x 轴向作一维线性插值得到 f(x, y1):
$$
f(x,y_0)=\frac{x_1-x}{x_1-x_0}f(x_0,y_0)+\frac{x-x_0}{x_1-x_0}f(x_1,y_0)
$$
$$
f(x,y_1)=\frac{x_1-x}{x_1-x_0}f(x_0,y_1)+\frac{x-x_0}{x_1-x_0}f(x_1,y_1)
$$
然后再由 (x, y0) 和 (x, y1) 在 y 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y):
$$
f(x,y)=\frac{y_1-y}{y_1-y_0}f(x,y_0)+\frac{y-y_0}{y_1-y_0}f(x,y_1)
$$
合并上述式子,得到最终的双线性插值结果:
$$
f(x,y)=\frac{(y_1-y)(x_1-x)}{(y_1-y_0)(x_1-x_0)}f(x_0,y_0)+\frac{(y_1-y)(x-x_0)}{(y_1-y_0)(x_1-x_0)}f(x_1,y_0)+\frac{(y-y_0)(x_1-x)}{(y_1-y_0)(x_1-x_0)}f(x_0,y_1)+\frac{(y-y_0)(x-x_0)}{(y_1-y_0)(x_1-x_0)}
$$
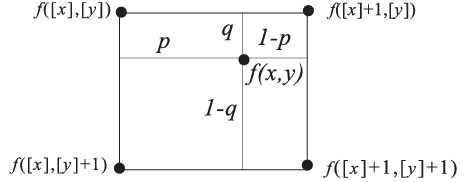
值得注意的是,在实际的图像插值处理过程中,为尽量保证插值效果的准确性,往往仅采用距离待插值点(转换至原图像坐标)最近的四个点,即:([]符号表示待插值点转换至原图像坐标后向下取整)
$$
x_0=[x],y_0=[y]
$$
$$
x_1=x_0+1,y_1=y_0+1
$$
从加权求和的角度理解,可以进一步地将双线性插值结果改写为如下形式:
$$
p=x-[x], q=y-[y]
$$
$$
\begin{array}{rcl}f(x,y)=(1-q){(1-p)f([x][y])+pf([x]+1,[y])}+q{(1-p)f([x],[y]+1)+pf([x]+1,[y]+1)}\end{array}
$$
基于以上算法思想,编写python函数代码实现图像放缩与旋转过程中的双线性法插值:
1 | # 双线性法插值实现图像放缩 |
双立方法
双立方法插值又称立方卷积插值/双三次插值,这也是数值分析中最常用的二维插值方法。在这种方法中,插值点 (x, y) 的像素颜色值 f(x, y) 通过矩形网格中最近的十六个采样点的加权平均得到,而各采样点的权重由该点到待求插值点的距离确定,此距离包括水平和竖直两个方向上的距离。相比之下,双线性插值仅由周围的四个采样点加权得到。
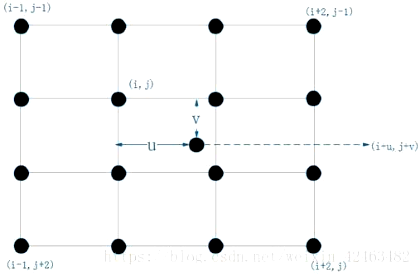
如上图所示,设(转换至原图像中)待求插值点坐标为 (i+u, j+v)【i、j为整数部分,u、v为小数部分】,已知其周围的 16 个像素坐标点 (网格) 的颜色值,还需要计算 16 个点各自的权重。以像素坐标点 (i, j) 为例,因为该点在 y 轴和 x 轴方向上与待求插值点 (i+u, j+v) 的距离分别为 u 和 v,所以其权重为 w(u) × w(v),其中 w(·) 是插值权重核 (可以理解为定义的权重函数)。同理可得其余 15 个像素坐标点各自的权重。那么,待求插值点 (i+u, j+v) 的颜色值 f(i+u, j+v) 将通过如下计算得到:
$$
f(i+u,j+v)=A\times B\times C
$$
其中各项由向量或矩阵表示为:
$$
\mathrm{A}=[w(1+u)w(u)w(1-u)w(2-u)]
$$
$$
\mathrm{B}=\begin{bmatrix}f(i-1,j-1)&f(i-1,j+0)&f(i-1,j+1)&f(i-1,j+2)\f(i+0,j-1)&f(i+0,j+0)&f(i+0,j+1)&f(i+0,j+2)\f(i+1,j-1)&f(i+1,j+0)&f(i+1,j+1)&f(i+1,j+2)\f(i+2,j-1)&f(i+2,j+0)&f(i+2,j+1)&f(i+2,j+2)\end{bmatrix}
$$
$$
\mathbb{C}=[w(1+v)w(v)w(1-v)w(2-v)]^T
$$
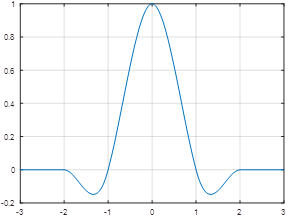
插值权重核 w(·) 为:
$$
w(x)=\begin{cases}1-2|x|^2+|x|^3&,|x|<1\4-8|x|+5|x|^2-|x|^3&,1\leq|x|<2\0&,|x|\geq2&\end{cases}
$$
插值权重核 w(·) 的函数图像:
为方便后续算法实现,将以上加权求和过程各步骤展开,合并后化简得到待插入点的颜色值计算公式:
$$
f(i+u,j+v)=\sum_{m=0}^{3}\sum_{n=0}^{3}a_{mn}u^{m}v^{n}
$$
其中多项式的系数a_{mn}计算公式如下:(式中p {qr}与上述矩阵B中元素一一对应,如p 00=f(i-1,j-1))
$$
\begin{aligned}
&a{00}=p{11}\&a_{01}=-\frac{1}{2}p_{10}+\frac{1}{2}p_{12}\&a_{02}=p_{10}-\frac{5}{2}p_{11}+2p_{12}-\frac{1}{2}p_{13}\&a_{03}=-\frac{1}{2}p_{10}+\frac{3}{2}p_{11}-\frac{3}{2}p_{12}+\frac{1}{2}p_{13}\&a_{10}=-\frac{1}{2}p_{01}+\frac{1}{2}p_{21}\&a_{11}=\frac{1}{4}p_{00}-\frac{1}{4}p_{02}-\frac{1}{4}p_{20}+\frac{1}{4}p_{22}\&a_{12}=-\frac{1}{2}p_{00}+\frac{1}{4}p_{01}-p_{02}+\frac{1}{4}p_{03}+\frac{1}{2}p_{20}-\frac{5}{4}p_{21}+p_{22}-\frac{1}{4}p_{23}\&a_{13}=\frac{1}{4}p_{00}-\frac{3}{4}p_{01}+\frac{3}{4}p_{02}-\frac{1}{4}p_{03}-\frac{1}{4}p_{20}+\frac{3}{4}p_{21}-\frac{3}{4}p_{22}+\frac{1}{4}p_{23}\
&a_{20}=p_{01}-\frac{5}{2}p_{11}+2p_{21}-\frac{1}{2}p_{31}\
&a_{21}=-\frac{1}{2}p_{00}+\frac{1}{2}p_{02}+\frac{5}{4}p_{10}-\frac{5}{4}p_{12}-p_{20}+p_{22}+\frac{1}{4}p_{30}-\frac{1}{4}p_{32}\&a_{22}=p_{00}-\frac{5}{2}p_{01}+2p_{02}-\frac{1}{2}p_{03}-\frac{5}{2}p_{10}+\frac{25}{4}p_{11}-5p_{12}+\frac{5}{4}p_{13}+2p_{20}-5p_{21}+4p_{22}-p_{23}-\frac{1}{2}p_{30}+\frac{5}{4}p_{31}-p_{32}+\frac{1}{4}p_{33}\
&a_{23}=-\frac{1}{2}p_{00}+\frac{3}{2}p_{01}-\frac{3}{2}p_{02}+\frac{1}{2}p_{03}+\frac{5}{4}p_{10}-\frac{15}{4}p_{11}+\frac{15}{4}p_{12}-\frac{5}{4}p_{13}-p_{20}+3p_{21}-3p_{22}+p_{23}+\frac{1}{4}p_{30}-\frac{3}{4}p_{31}+\frac{3}{4}p_{32}-\frac{1}{4}p_{33}\
&a_{30}=-\frac{1}{2}p_{01}+\frac{3}{2}p_{11}-\frac{3}{2}p_{21}+\frac{1}{2}p_{31}\
&a_{31}=\frac{1}{4}p_{00}-\frac{1}{4}p_{02}-\frac{3}{4}p_{10}+\frac{3}{4}p_{12}+\frac{3}{4}p_{20}-\frac{3}{4}p_{22}-\frac{1}{4}p_{30}+\frac{1}{4}p_{32}\&a_{32}=-\frac{1}{2}p_{00}+\frac{5}{4}p_{01}-p_{02}+\frac{1}{4}p_{03}+\frac{3}{2}p_{10}-\frac{15}{4}p_{11}+3p_{12}-\frac{3}{4}p_{13}-\frac{3}{2}p_{20}+\frac{15}{4}p_{21}-3p_{22}+\frac{3}{4}p_{23}+\frac{1}{2}p_{30}-\frac{5}{4}p_{31}+p_{32}-\frac{1}{4}p_{33}\&a_{33}=\frac{1}{4}p_{00}-\frac{3}{4}p_{01}+\frac{3}{4}p_{02}-\frac{1}{4}p_{03}-\frac{3}{4}p_{10}+\frac{9}{4}p_{11}-\frac{9}{4}p_{12}+\frac{3}{4}p_{13}+\frac{3}{4}p_{20}-\frac{9}{4}p_{21}+\frac{9}{4}p_{22}-\frac{3}{4}p_{23}-\frac{1}{4}p_{30}+\frac{3}{4}p_{31}-\frac{3}{4}p_{32}+\frac{1}{4}p_{33}
\end{aligned}
$$
基于以上算法思想,编写python函数代码实现图像放缩与旋转过程中的双立方法插值:
1 | # 双立方法插值实现图像放缩 |
图像插值算法优化:基于四平面
在上述的多种基于分段插值的图像插值算法中,均采用f(i, j)来表示图像的像素点坐标处的颜色值,其中i表示行坐标,j表示列坐标。为进一步地体现图像的局部特征差异并将其用于插值过程,我们引入“平面”的概念,并对图像数据进行升维处理,用三维空间点(i, j, f(i, j))来表示一个像素,并将其对应至空间坐标系中的一个点(x, y, z)。
对一个待插入点而言,可以通过坐标平移将其周围4 个像素点转换为:(注意:此处z0z3为像素坐标点s0s3的颜色值,下同)
$$
s_0(0,0,z_0),s_1(0,1,z_1),s_2(1,0,z_2),s_3(1,1,z_3)
$$
从上述4个点的坐标可以看出它们任意3个点一定不在同一条直线上, 不在同一直线上的3个点可以确定一个平面, 下面讨论具体的插值方法:
先求出这4个点可能的4个平面方程
已知空间平面的一般方程为:
$$
Ax+By+Cz+D=0
$$
将s0、s1、s2分别带入上式可得:
$$
\begin{cases}Cz_0+D=0\B+Cz_1+D=0\A+Cz_2+D=0&\end{cases}
$$
则有:
$$
D=-Cz_0,B=C(z_0-z_1),A=C(z_0-z_2)
$$
再将其带回空间平面方程,整理后用f(x, y)代替z得到插值公式:
$$
f(x,y)=(z_{2}-z_{0})x+(z_{1}-z_{2})y+z_{0}
$$
同理,将s0、s1、s3带入空间平面方程可得插值公式:
$$
f(x,y)=(z_{3}-z_{1})x+(z_{1}-z_{0})y+z_{0}
$$
将s0、s2、s3带入空间平面方程可得插值公式:
$$
f(x,y)=(z_{2}-z_{0})x+(z_{3}-z_{2})y+z_{0}
$$
将s1、s2、s3带入空间平面方程可得插值公式:
$$
f(x,y)=(z_{3}-z_{1})x+(z_{3}-z_{2})y+(z_{2}+z_{1}-z_{3})
$$如果s0、s1、s2、s3这4 个点在同一平面上, 则使用上述任意一个插值公式进行插值均可。 【平面法】
判断这4个点是否在同一平面上, 只需要比较z1+z2 与 z0+z3是否相等:
线段s0s3中点坐标为
$$
(\frac12,\frac12,\frac{z_0+z_3}2)
$$
线段s1s2中点坐标为
$$
(\frac12,\frac12,\frac{z_1+z_2}2)
$$
如果它们的中点坐标相同,则说明两条线段相交,相交的两条直线可以决定一个平面,即如果待插人点周围的四个点满足:
$$
z_1+z_2=z_0+z_3
$$
则这它们就是同一平面上的 4 个点,否则就不是同一平面上的 4 个点。从4个可能的平面中选择一个平面进行插值【四平面法】
如果它们不是同一平面上的4个点, 情况比较复杂, 需认真讨论,s0、s1、s2、s34个点的位置关系如下图所示:
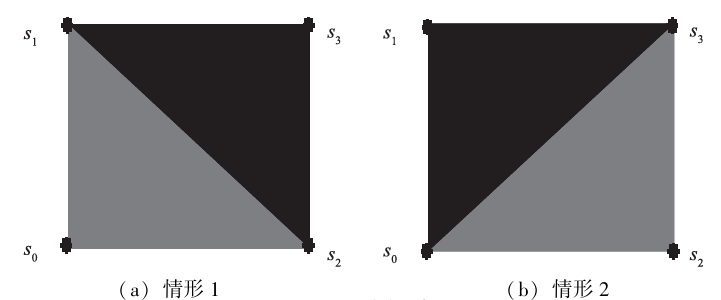
在插值的过程中如果一半的区域选择由s0、s1、s2 所确定的平面进行插值, 则另一半必须选择由s1、s2、s3所确定的平面进行插值, 以保证对角线的每一边都是在同一个平面上, 避免出现 “锯齿形” 边缘,为了便于描述, 称s0、s1、s2所确定的平面为 “左下平面”,s1、s2、s3 所确定的平面为 “右上平面”,s0、s1、s3 所确定的平面 “左上平面”,s0、s2、s3所确定的平面 “右下平面”。 为此, 需要参考周围其他点的情况以决定选择哪个平面进行插值。 具体情况如下图所示(黑点是待插入点周围的4个点,白点是参考点):
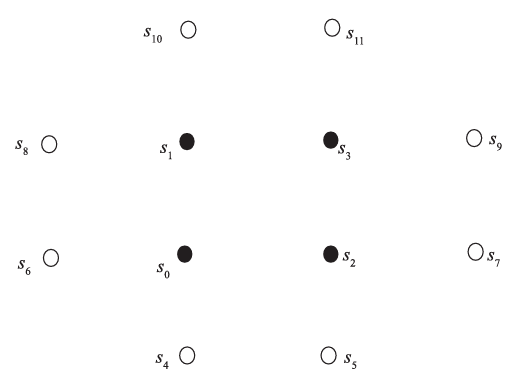
- 对于“左下平面”, 只能参考s0、s1、s2三点左面和下面的点, 即s0、s1、s2三点与s4、s5、s6、s8四个点中的任意一点在同一平面上即可。
- 对于“右上平面”,只能参考s1、s2、s3三点右面和上面的点, 即s1、s2、s3三点与s7、s9、s10、s11四个点中的任意一点在同一平面上即可。
- 对于 “左上平面”,只能参考s0、s1、s3三点左面和上面的点, 即s0、s1、s3三点与s6、s8、s10、s11四个点中的任意一点在同一平面上即可。
- 对于 “右下平面”,只能参考s0、s2、s3三点右面和下面的点, 即s0、s2、s3三点与s4、s5、s7、s9四 个点中的任意一点在同一平面上即可。
针对1、2两种情况, 当y = 1 + x时,用 “左下平面” 进行插值, 否则用 “右上平面” 进行插值;针对3、4两种情况, 当y = x ^ 3时,用 “左上平面” 进行插值, 否则用 “右下平面” 进行插值。
判断4个点在同一平面上的方法:(以情况1为例)
对于判断s0、s2、s1、s8 4 点是否在同一平面上, 只需要判断z0 + z1与z2 + z8是否相等即可;
对于s0、s1、s2、s5 4点, 只需要判断z0 + z2与z1 + z5是否相等即可;
对于s0、s1、s2、s6 4点:如果s0、s2、s6 3点在同一直线上, 则直线外一点s1与该直线就可以确定一个平面,而要判断这三点是否在同一直线上,只需判断z2 + z6与2 * z0是否相等即可【线段s2(1, 0, z2) s6(-1, 0, z6) 的中点坐标为(0, 0, z2 + z6),若z2 + z6 = 2 * z0, 则点s0(0, 0, z0)就是它们的中点坐标,当然这3点就在同一条直线上】;
对于s0、s1、s2、s4 4点, 与s0、s1、s2、s6 4 点的情况相同。
如果2和3两点中的情形均不满足, 说明待插入点周围的情况太复杂(不符合平面插值), 此时采用双线性法进行插值。
基于以上算法思想,编写python函数代码实现图像放缩与旋转过程中的四平面法插值:
1 | # 四平面法插值实现图像放缩 |
实验测试结果分析
一个理想的插值算法对一幅图像逆时针旋转若干度,再顺时针旋转若干度,应该与原图像相同;同理,对一幅图像放大若干倍,再缩小若干倍,也应该与原图像相同。 基于此,将下面的4幅图像分别用4种算法先逆时针旋转45°,再顺时针旋转45°;先放大4倍,再缩小4倍,然后分别用峰值信噪比(PSNR)验证各算法的优劣。




从定性实验的效果角度,上述四幅图像通过常用的三种分段插值算法完成上述的放大与旋转任务后得到的结果如下图所示:

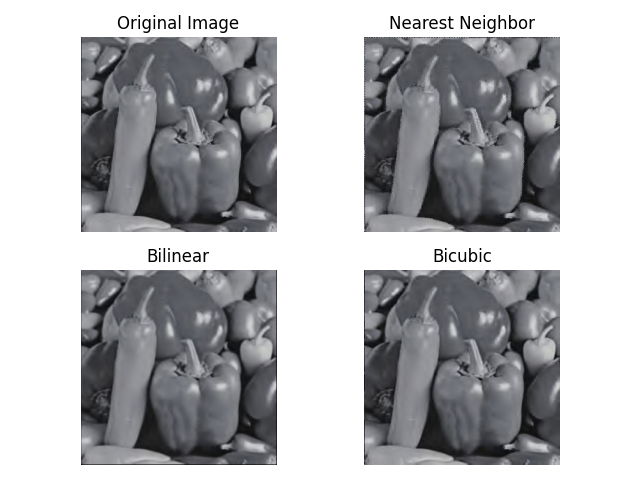
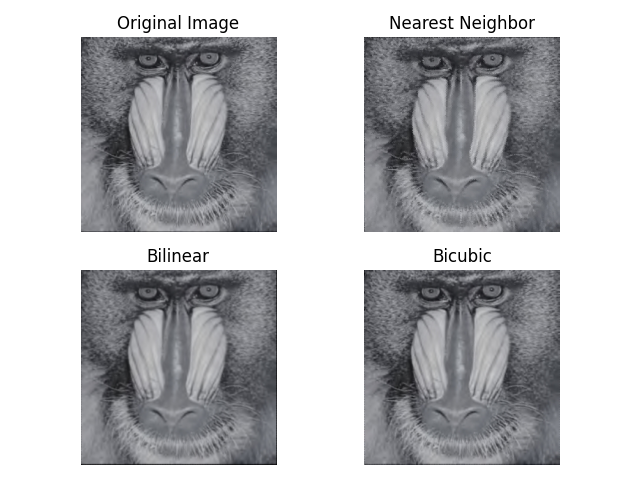

从实验结果上来看,最近邻算法的边缘颜色“最醒目”,且出现了较为严重的“锯齿形”边缘现象;双线性算法的边缘颜色“最暗淡”;双线性算法和双三次算法也有“锯齿形”边缘现象, 但视觉效果相比最近邻算法而言并不明显。
通过改进的四平面插值算法,对上述四幅图像完成上述的放大与旋转任务后得到的结果如下图所示:

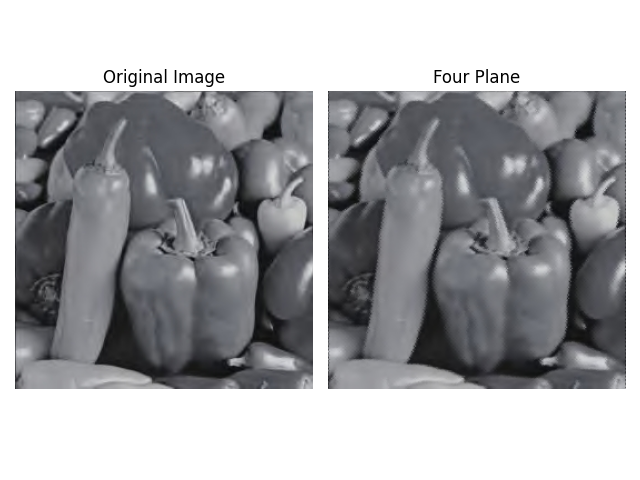
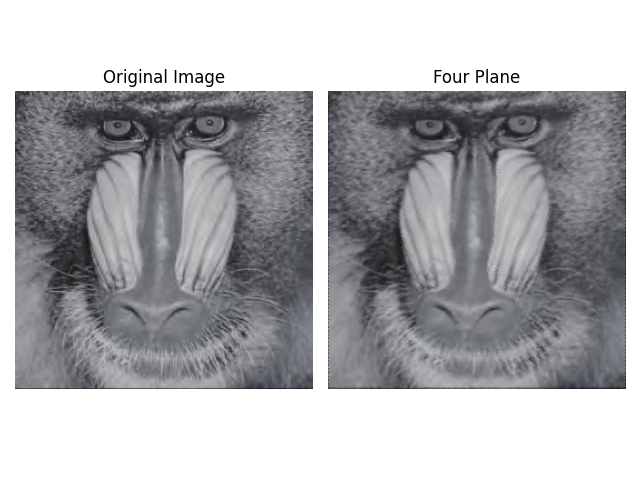

可以看到,四平面插值算法处理后的图像斜线边缘部分是 “光滑连续” 的, 视觉效果比较好,同时有效避免了“锯齿形”边缘现象和“马赛克”现象。
从定量实验的数据角度,我们对于各图像用不同算法完成上述旋转与放缩任务后得到的图像峰值信噪比与算法运行时间进行了计算与统计,结果如下表所示:
峰值信噪比(PSNR)用于表示信号的最大可能功率与影响其表示的保真度的破坏噪声的功率之间的比率。PSNR在图像处理上主要用于量化受有损压缩影响的图像和视频的重建质量。
PSNR 通过均方误差( MSE ) 定义。
给定一个无噪声的m×n单色图像I及其噪声近似值K,MSE定义为:
$$
MSE=\frac{1}{mn}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}[I(i,j)-K(i,j)]^2.
$$
故PSNR定义为:
$$
\begin{aligned}\mathrm{PSNR}&=10\cdot\log_{10}\left(\frac{MAX_I^2}{MSE}\right)\&=20\cdot\log_{10}\left(\frac{MAX_I}{\sqrt{MSE}}\right)\&=20\cdot\log_{10}(MAX_I)-10\cdot\log_{10}(MSE).\end{aligned}
$$
一般而言,通过PSNR来判断处理后图像的失真情况有如下通用结论:
- PSNR > 30 dB:图像质量较好,失真不明显。
- PSNR 20~30 dB:中等质量,存在可察觉失真。
- PSNR < 20 dB:质量较差,失真显著。
实际计算时,采用opencv自带的PSNR方法cv2.PSNR(img, output)对原始图像与处理后图像的PSNR进行比较计算。
| 测试图像 | 最近邻插值PSNR | 双线性插值PSNR | 双立方插值PSNR | 四平面插值PSNR |
|---|---|---|---|---|
| 琳娜(269*269) | 20.74217399 | 27.11906575 | 29.36532325 | 36.70765842 |
| 辣椒(268*268) | 22.92424674 | 27.91435345 | 31.04713312 | 39.25866529 |
| 狒狒(268*268) | 21.8194312 | 28.06968286 | 29.12614241 | 38.2193871 |
| 房子(256*256) | 22.34146151 | 26.21366716 | 30.67389681 | 38.8204405 |
| 插值算法 | 最近邻法 | 双线性法 | 双立方法 | 四平面法 |
|---|---|---|---|---|
| 算法运行平均用时 | 0.678485751 | 3.293492556 | 92.66596091 | 15.02119243 |
通过对比上述定量实验结果可以发现,在传统的三种分段插值算法中,随着运算阶数(采样待插值点周围的原图像像素点颜色值信息)的增加,图像经过放缩与旋转处理后的失真程度有明显降低,但仍大致处于存在可察觉失真的区间,且算法运行用时也逐渐增加(事实上双立方法的实现可以在编程层面实现优化,这里只是为更直观地展现O(n^2)时间复杂度在图像大小达到一定规模时的显著影响);而引入的四平面算法不仅在失真程度上较传统的插值算法均有显著改善,算法运行用时也明显优于传统算法中效果最好的双立方法。
综合以上的定性与定量实验结果及分析,本文提出的基于四平面的图像插值算法在图像处理效果(失真)与运行效率上均较传统算法有明显提升,这充分证明了该算法的有效性。
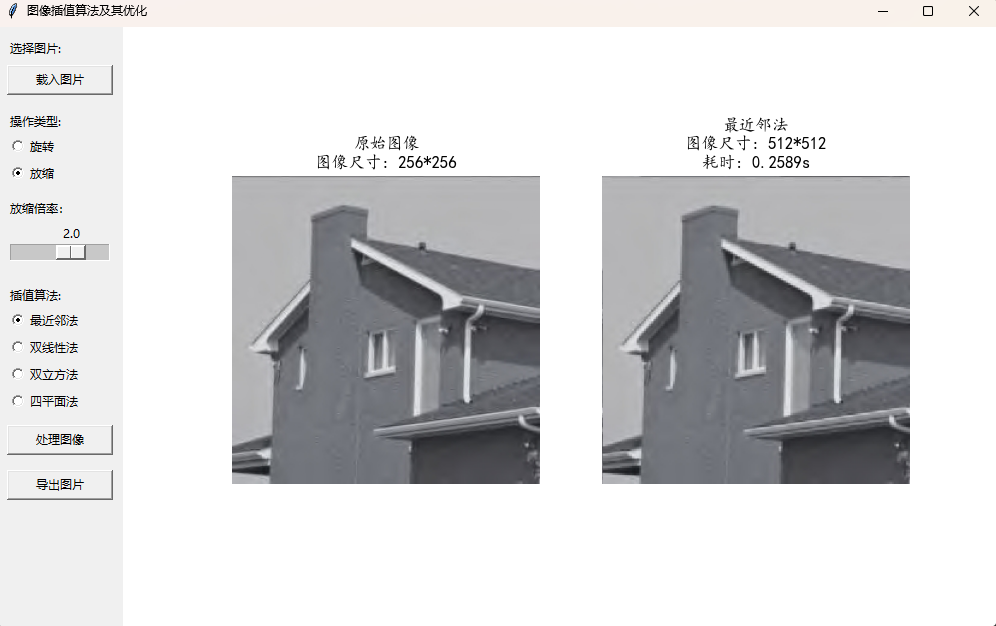
将上文提到的全部四种算法及旋转与放缩两种功能集成到基于python的gui可视化系统中,并打包成exe可执行文件,制作了一个基于插值的图像处理系统,基本功能演示如下图所示:

参考文献
[1] 王开荣,杨大地编著.应用数值分析[M].高等教育出版社,2010.
[2] 毛伟伟,于素萍,石念峰.一种基于四平面的图像插值算法[J].洛阳理工学院学报(自然科学版),2024,34(01):76-81.
[3] 刘显德,李笑.任意大小图像的量子描述及双线性插值方法[J].计算机工程与设计,2024,45(08):2423-2432.
[4] 张喜民,詹海生.基于双三次插值的Canny-Devernay亚像素图像边缘检测算法[J].现代制造工程,2025,(03):107-114.
[5] 陈玲玲,周宁,殷永,等.插值方法在光声图像重建中的应用[J].计算机与数字工程,2013,41(10):1676-1677+1694.