选题背景与意义

微分方程是数学中一个重要且广泛应用的领域，涉及到描述变化和相互关系的方程。它是一种包含导数或微分的方程，常用于自然现象建模以及解决科学和工程领域中的问题。微分方程研究是数学中的一个重要分支，涵盖了广泛的领域和应用。通过研究微分方程，我们可以理解和预测自然现象的行为，以及解决科学和工程中的实际问题。同时，微分方程的研究也促进了数学的发展和数学工具在其他学科中的应用。

常微分方程被广泛应用于物理、生物、化学、经济学等各个领域。在许多情况下，观测数据是已知的，而其中隐含的微分方程仍然难以捉摸。因此，数据驱动的常微分方程(或动力系统)发现和反演是一个重要的研究方向。

微分方程反演问题是相对于微分方程的求解而言的：

• 微分方程的求解通常是一个正向问题，即给定初始条件，求解关于未知函数的方程；
• 微分方程反演问题是指根据已知的结果，推导出产生这些结果的微分方程，是从结果向方程的逆向推导和反演。

在数学上，微分方程的反演问题具有一系列的数学挑战和困难：

• 反问题的病态性：微小扰动在反问题的输出中会导致较大的误差，因此需要稳定性分析和正则化方法来解决数值计算中的误差；
• 存在非唯一解情况：需要利用先验信息、约束条件和经验知识等来进行问题的约束和规定，以得到合理的解。

微分方程反演问题研究在数学理论和实际应用中具有重要意义。通过解决微分方程的反演问题，我们可以从有限的观测数据中重建和推断未知的边界条件、初始条件或未知函数，从而深入理解系统的行为和性质，并提供科学、工程和医学等领域的相关应用。

随着计算机技术的发展，数值计算和机器学习在微分方程反演问题研究中的应用也呈现出迅猛发展的趋势。传统的微分方程推断方法依赖于领域专家的知识和经验，而机器学习方法，如神经网络、深度学习和遗传算法等，可以自动从大量数据中学习模式和关系，从而更准确地推断出微分方程模型。如今我们可以获取到大规模的、高维度的数据集，这为从数据中推断微分方程提供了更多的信息和挑战。而传统的模型推断方法在处理大数据集时可能受到维度灾难和计算复杂度的限制。机器学习的强大计算能力和自适应建模能力为解决这些问题提供了新的思路。

利用机器学习从数据中反演微分方程的方法可以分为两个方面：

• 在模型选择方面，机器学习可以通过自动搜索和学习合适的微分方程模型，利用测度函数或结构特征来评估不同模型的性能，并选择最适合数据的微分方程模型；
• 在参数估计方面，机器学习可以利用大数据集中的样本来优化微分方程模型的参数，以最小化模型与实际数据之间的误差。

利用机器学习从数据中反演微分方程是微分方程和机器学习交叉领域的重要研究方向。它利用机器学习的能力和大数据的优势，可以更准确地建模和预测复杂的动力学系统，推进科学研究和实际应用的发展。

针对常微分方程，目前常用的反演方法有如下几种：

• 高斯过程：将高斯过程置于状态函数之上，然后通过最大化边际对数似然性从数据中推断参数，这种方法适用于解决高维问题，但是对系统的形式有限制，并且仅用于估计系统的参数。
• 符号回归：创建并更正与观测数据相对应的符号模型，为控制函数提供更具表现力的函数形式，但缺点是对于大型系统来说计算成本高，并可能容易过拟合。
• 稀疏回归：找到候选基函数的稀疏组合来近似控制函数，其系数由最小二乘法或贝叶斯回归确定。这种方法提供系统的明确形式，不需要太多先验知识，但是依靠适当的候选函数；对于没有简单或稀疏表示的复杂动力系统来说可能是低效的。
• 统计学习：通过最小化经验误差来学习系统在某个假设空间中的相互作用核，避免维度诅咒，可以发现非常高维度的系统，但是仅适用于具有交互作用的核函数的动力系统。
• 物理信息神经网络（PINN）：一种新的深度学习方法，用于解决非线性偏微分方程的正问题和反问题。通过在前馈神经网络中嵌入由偏微分方程描述的物理信息，在不需要标签数据的情况下，将 PINN 训练为偏微分方程的近似解的代理模型。受此启发，进一步发展出了多步神经网络LMNets，这本质上是使用给定相点上的流映射提供的信息来反演动力系统种的未知控制函数f的一种逆过程。

在数值分析中，发展高阶方法是许多应用中的一个重要课题。传统上，在求解动力系统时，高阶离散化技术，如线性多步法和龙格-库塔方法已经得到了发展。近年来，线性多步法也被用于动力系统的发现。随着使用深度学习的发现取得令人满意的进展，对它在动力系统发现的理论理解也在进一步发展。

基于以上所陈述的微分方程反演问题的研究现状，针对无显式方程的非线性系统这一在真实物理世界中更为广泛且常见的情形，我们希望基于高阶离散化技术线性多步法，结合多步神经网络LMNets这一深度学习方法，拟合和反演出数据背后的动力学物理规律。

算法框架与原理

研究对象——常微分方程（组）

首先明确我们的研究对象——常微分方程：
$$
\begin{aligned}&\frac{dx(t)}{dt}=f(x(t),t),\&x(t_{0})=x_{0}\end{aligned}
$$
上述式子是一个最简单的二维常微分方程示例，其中x(t) ∈ R是关于时间t的函数，函数关系由一个微分方程刻画，且给出了一定的初值条件以唯一确定函数x的表达式，从而能够真实地刻画物理过程随时间变化的发展情况。

事实上大多数时候我们需要观测的物理量远远不止x这一个，因此为了后续更容易推广到高维情形（后续无特别说明，均围绕自治常微分方程展开讨论），我们将上述的非自治常微分方程转化为向量化的自治常微分方程：
$$
\begin{aligned}&\frac{d\boldsymbol{u}(t)}{dt}=\hat{f}(\boldsymbol{u}(t)),\&\boldsymbol{u}(t_{0})=\boldsymbol{u}{0}\end{aligned}
$$
其中：
$$
u=(x,y)\in\mathbb{R}^{D+1},\hat{f}=(f,1)^{T},u{0}=(x_{0},t_{0})^{T}
$$
在反演问题中，已知在若干时刻节点t_1、t_2、…、t_n的解x的数据，我们一般不会希望直接解出x(t)的表达式，而是通过确定光滑函数f，从而利用给定的数据反演出微分方程。这样的传统是从简单的反演情形推广并沿用的，因为比起得到一个精确的函数表达式，我们更希望探究这个表达式背后的物理规律，而这往往离不开微分方程，因此保留微分方程的形式具有一定的必要性。

多步神经网络

线性多步法是用于微分方程数值求解的常用方法。传统上，它们用于求解给定常微分方程的解，可以称为微分方程的正问题。但线性多步法也可以用于反演给定解的原微分方程，属于微分方程的反问题，尤其是将线性多步法的经典数值方法与神经网络相结合，例如多步神经网络。

线性多步法

线性多步法是求解常微分方程数值解的一种常见方法。随着计算机技术的发展，线性多步法得到更加广泛的应用。人们逐渐发现，在某些情况下，线性多步法可以提供更高的数值精度和数值稳定性。此外，线性多步法可以与其他数值方法（如龙格-库塔法）结合使用，互补彼此的优点。

对于上述常微分方程（非自治），设其中结点总数为N，时间间隔h为常数:
$$
h = t_{n + 1} - t_n, n = 1, …, N - 1
$$
则第n个结点的步长为M的线性多步法有以下公式：
$$
\sum_{m=0}^{M}[\alpha_{m}x_{n-m}+h\beta_{m}f(x_{n-m},t)]=0,n=M、\ldots、N, \alpha_{_M}\neq0
$$
使用线性多步法求解常微分方程时，必须选择初始的步长M值，以及确定系数α、β的不同方法，然后可以依次计算n≥M的近似值x_n。

事实上，根据确定系数的方法不同，线性多步法也分为多种类型，本项目中主要使用如下的三种常见的线性多步法：

• Adams-Moulton 法：作为一种隐式方法，需要通过迭代或其他数值求解技术来解决每个时间步长的方程组。它在求解非刚性和刚性常微分方程时都表现良好，并且具有较高的数值稳定性，其精度随步长的减小而提高，但响应地可能会产生更高的计算代价。对于高阶常微分方程，Adams-Moulton 法需要结合相应的差分格式将高阶常微分方程转化为一阶方程组进行求解。

$$
\sum_{m=0}^M\alpha_mx_{n-m}=h\sum_{m=0}^M\beta_mf(x_{n-m})
$$

• Adams-Bashforth法：作为一种显式方法，在求解非刚性和刚性常微分方程时都表现良好，计算效率较高，并且容易实现，但可能会收到稳定性条件地限制，其精度随步长的减小而提高。对于高阶常微分方程，Adams-Bashforth法需要结合相应的差分格式将高阶常微分方程转化为一阶方程组进行求解。

$$
\sum_{m=0}^M\alpha_mx_{n-m}=h\sum_{m=0}^M\beta_mf(x(t_{n-m}))
$$

• 后向微分公式法(Backward Differentiation Formula, BDF)：同样是一种隐式方法，但与Adams-Moulton法不同，后向微分公式法是通过解一个非线性方程组来得到当前时间步长的数值解。这个方程组可以用牛顿迭代等数值求解技术来解决。该方法具有较好的数值稳定性，其精度依赖于使用的插值多项式的阶数。一般来说，其高阶形式可以提供更高的精度，但也会增加计算的复杂性。它适用于求解非刚性和刚性常微分方程，并且在稳定性和数值精度方面通常有良好的表现。

$$
\sum_{m=0}^{M}\alpha_{m}x_{n-m}=h\beta f(x(t_{n}))
$$

除此之外，即使采用同一种系数确定方式，选择的步长M不同，得到的系数α、β也有所不同。具体而言，本项目中针对以上三种线性多步法，分别选取步长M=2/3/4的三种情况进行实验测试，下面列出各方法对应不同步长时的系数情况：

线性多步法的优点在于其高阶的精度和较小的计算代价，可以有效地逼近微分方程的数值解。但线性多步法可能会受到稳定性和初始条件的限制，选择适当的步长和求解方法非常重要。

多步神经网络算法

从线性多步法的公式中得到启发，可以用神经网络去反演常微分方程右端的f。通过相等时间间隔h的数值解x的数据训练神经网络，该神经网络的参数可以通过使以下均方误差损失函数MSE最小化来训练得到：
$$
MSE=\frac{1}{N-M+1}\sum_{n=M}^N\parallel y_n\parallel^2
$$
其中：
$$
y_n=\sum_{m=0}^M\left[\alpha_mu_{n-m}+h\beta_mf_{NN}(u_{n-m})\right],n=M,\ldots,N
$$
式中f_NN表示神经网络对函数f的近似，y_n也称为线性多步法（LMM）残差。

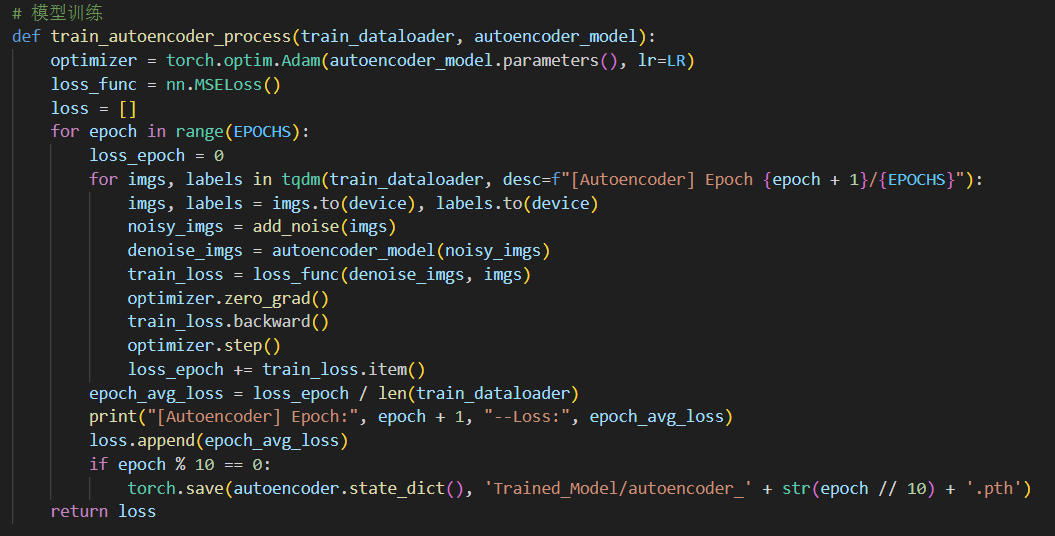
在Python中编写函数train()以封装多步神经网络的训练流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 模型训练 
def train(u_tensor, model, loss_func, h, M): 
    # 参数说明：训练集u_tensor,待训练模型model,损失函数loss_func,时间步长h,步数M,最大训练次数EPOCH
    optimizer = torch.optim.Adam(model.parameters(), lr=LR)
    loss_history = []
    
    for epoch in range(EPOCHS):          
        model.train()        
        batch_u = u_tensor.to(device)        
        train_loss = loss_func(batch_u, model, h, M)   
        optimizer.zero_grad()      
        train_loss.backward()    
        optimizer.step()    
        epoch_avg_loss = train_loss.item()         
        loss_history.append(epoch_avg_loss) 
    
    return loss_history

其中loss_func即为上述定义的均方误差损失函数MSE：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 损失函数
def loss_func(u, model, h, M):
	# 参数说明：模型输入数据u,待训练模型model,时间步长h,步数M

    # 根据选定的方法确定系数α、β（示例：Adams-Moulton法，M=4）
    alpha = [1, -1, 0, 0, 0]
    beta = [251/720, 646/720, -264/720, 106/720, -19/720]
        
    loss = 0.0
    for n in range(M, len(u)):
        residual = 0.0
        for m in range(M+1):
            u_nm = u[n - m].unsqueeze(0)
            f_nm = model(u_nm)
            residual += alpha[m] * u[n - m] + h * beta[m] * f_nm.squeeze()
        loss += torch.norm(residual) ** 2
    return loss / (len(u) - M + 1)

基于多步神经网络改进的常微分方程反演算法

改进的多步神经网络算法

多步神经网络做出了比较理想的假设，即给出了所有的数值解数据是无噪声的，以及神经网络可以表示对常微分方程产生零残差的反演。这种假设是理想化的，我们可以在实际情况下使用改进的方法尝试发现未知常微分方程。

对于多步神经网络，除线性多步法残差之外，如果神经网络能够满足一些通用近似性质，尤其是在多步神经网络反演法效果不佳的非自治常微分方程的反演问题中，可以扩展精确和完整数据的收敛结果。考虑到神经网络对函数近似的强大能力（见通用近似定理），这意味着至少在合适的光滑的常微分方程中存在良好的泛化误差。

假设数据集为给定在若干时刻t_1、t_2、…、t_N的方程的数值解u的值，把每一时刻t_n对应的解u(t_n)记为u^(n)，而t_n对应的导数数据一般无从得知。当时间间隔h较小时，可用二阶中心差分法近似求出导数数据，记对于每一时刻t_n求出的导数数据为d^(n)，则：
$$
d^{(n)}=\begin{cases}(-3\boldsymbol{u}^{(n)}+4\boldsymbol{u}^{(n+1)}-\boldsymbol{u}^{(n+2)})/2h,\quad n=1,\(\boldsymbol{u}^{(n+1)}-\boldsymbol{u}^{(n-1)})/2h,\quad1<n<N,\(\boldsymbol{u}^{(n-2)}-4\boldsymbol{u}^{(n-1)}+3\boldsymbol{u}^{(n)})/2h,\quad n=N.&\end{cases}
$$
显然二阶中心差分法求导数d^(n)的误差为o(h^2)。

对于常微分方程的反演，我们改进了多步神经网络的损失函数，其中既包含解数据，又包含导数数据：
$$
L=l_1(u,d)+l_2(u,d,f_{NN})
$$
其中：
$$
l_{1}=\frac{1}{N-M+1}\sum_{n=M}^{N}\left|\sum_{m=0}^{M}[\alpha_{m}u_{n-m}+h\beta_{m}f_{NN}(u_{n-m})]\right|^{2}
$$

$$
l_{2}=\frac{1}{N-M+1}\sum_{n=M}^{N}\left|f_{NN}(u_{n})-d_{n}\right|^{2}
$$

$$
n=M,\ldots,N
$$

式中向量范数采用二范数；u为数值解的数据，d为二阶中心差分法得到的导数数据，则有：

• l_1：线性多步法残差，可以表示常微分方程的近似程度
• l_2：均方误差函数，可以表示网络结构的准确度

把u^(n)作为输入，d^(n)作为期望输出进行训练，得到的f_NN即为对函数f的近似。训练流程与改进后的损失函数Python实现如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 模型训练 
def train(u_tensor, model, loss_func, h, M): 
    # 参数说明：训练集u_tensor,待训练模型model,损失函数loss_func,时间步长h,步数M,最大训练次数EPOCH
    optimizer = torch.optim.Adam(model.parameters(), lr=LR)
    loss_history = []
    
    for epoch in range(EPOCHS):
        model.train()
        batch_u = u_tensor.to(device)
        batch_d = d_tensor.to(device)
        train_loss = loss_func(batch_u, batch_d, model, h, M)
        optimizer.zero_grad()
        train_loss.backward()
        optimizer.step()
        epoch_avg_loss = train_loss.item()
        loss_history.append(epoch_avg_loss)
        
    return loss_history

可以看到，与改进前相比，在训练过程中增加了对二阶中心差分法得到的导数的相关计算，进一步利用了训练数据中的信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# 损失函数
def loss_func(u, d, model, h, M):
    # 参数说明：模型输入数据u,输入数据对应的真实微分数据d,待训练模型model,时间步长h,步数M

    # 根据选定的方法确定系数α、β（示例：Adams-Moulton法，M=4）
    alpha = [1, -1, 0, 0, 0]
    beta = [251/720, 646/720, -264/720, 106/720, -19/720]
        
    # 多步法残差 l1
    l1 = 0.0
    for n in range(M, len(u)):
        residual = 0.0
        for m in range(M+1):
            u_nm = u[n - m].unsqueeze(0)
            f_nm = model(u_nm)
            residual += alpha[m] * u[n - m] + h * beta[m] * f_nm.squeeze()
        l1 += torch.norm(residual) ** 2
    l1 = l1 / (len(u) - M + 1)
    
    # 导数拟合误差 l2
    pred_d = model(u)
    l2 = torch.mean(torch.norm(pred_d - d, dim=1) ** 2)
    
    return l1 + l2  # 总损失

值得注意的是，针对非自治常微分方程，由于在将其变换为自治常微分方程时进行了升维操作，这意味着真实的导数向量在y=t这一分量上的值必然是1，因此后续在检验模型训练效果时可利用这一点对模型性能进行先决的把握。

基于误差界理论论证改进算法的优越性

在上述损失函数中，l_1是对目标函数的良好近似，而l_2是神经网络中常用的损失函数。考虑到神经网络对函数近似的强大能力，这意味着即使对于噪声数据，改进的方法也应有良好的泛化能力和鲁棒性。在这里，我们先从理论上来论证改进方法在泛化能力与鲁棒性上的优越性，后续的数值实验部分将采用三类非自治方程的反演来验证改进的多步神经网络的效果。

对于二分类问题（可推广至函数近似的回归问题），当假设空间是有限个函数的集合F={f_1,f_2,…,f_d}时，对任意一个函数f∈F,至少以概率1-δ，以下不等式成立：
$$
R(f)\leq\hat{R}(f)+\varepsilon(d,N,\delta)
$$
其中：
$$
\begin{gathered}R(f)=E[L(Y,f(X))]\\hat{R}(f)=\frac{1}{N}\sum_{1}^{N}L(y_{i},f(x_{i}))\\varepsilon(d,N,\delta)=\sqrt{\frac{1}{2N}(\log d+\log\frac{1}{\delta})}\end{gathered}
$$
式中，R(f)为泛化误差（测试集上的测试风险），\hat{R}(f)为训练集上的经验风险，\hat{R}(f) + ε(d,N,δ)即为泛化误差界。观察上式可知，泛化误差界与样本数N成正比，与假设空间包含的函数数量d成反比。因此，当样本数N越大，泛化误差界越小，当假设空间F包含的函数越多，泛化误差界越大。

根据上述定理，针对改进后的神经网络，有如下不等式成立：
$$
\left|f_{NN}(u^{(n)})-\hat{f}(u^{(n)})\right|\leq\left|f_{NN}(u^{(n)})-d^{(n)}\right|+\left|\hat{f}(u^{(n)})-d^{(n)}\right|\leq w+o(h^{2})
$$
该不等式表明，改进后的损失函数可以拆解成两部分误差：

• 第一部分为通过神经网络得到的导数近似值与通过二阶中心差分法求出的导数之间的误差，设该误差限为w；
• 第二部分为导数真实值与通过二阶中心差分法求出的导数之间的误差，根据二阶中心差分法的基本原理，其误差限为**o(h^2)**。

显然改进后的多步神经网络的泛化误差相较改进前有了进一步的约束，尤其显著减小了噪声对模型的影响，具有更强的泛化能力和鲁棒性。

数值实验与分析

为充分验证改进方法的泛化能力与鲁棒性，我们选取了六个实际的物理问题（对应常微分方程）作为测试用例，对应自治/非自治以及三种不同的线性多步法，在每一个测试用例内选取不同的线性多步法步数以及训练数据所含的高斯噪声方差，对改进前后的两种基于多步神经网络的常微分方程反演方法进行测试。下面我们以“受迫振动方程”这一用例详细展示测试流程，其他的测试用例仅作结果展示。

数值实验流程

数据构建

基于选定的测试用例对应的常微分方程，可采用如下步骤生成原始的真实数据集：

1. 在所给区域内均匀选取间隔为h的N个结点t_n,n=1,2,…,N ,使用Python中的Scipy库求出各结点对应的数值解u^(n)；
2. 将数值解u^(n) 代入二阶中心差分法中得到每个x_n 对应的导数值d^(n) ；
3. 噪声数据构建：在各结点对应的数值解u^(n) 上依次加上期望为0，方差为0、0.01、0.05的高斯噪声。

在Python中，用函数get_data()函数实现了数据构建的代码封装：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

def get_data(t0, t_end, h, y0, noise_std=0.0):     
    t_eval = np.arange(t0, t_end + h, h)     
    
    # 数值解    
    sol = solve_ivp(forced_oscillator, [t0, t_end], y0, t_eval=t_eval)    
    x = sol.y.T  # shape: [N, 2]     
    t = sol.t.reshape(-1, 1)  # shape: [N, 1]     
    
    # 添加高斯噪声     
    if noise_std > 0:         
        x += np.random.normal(0, noise_std, size=x.shape)      
        
    # 构造 u = [x1, x2, t]     
    u = np.hstack([x, t])      
    
    # 二阶中心差分求导数 d ≈ du/dt     
    d = np.zeros_like(u)     
    # 边界点使用前向/后向差分     
    d[0] = (-3 * u[0] + 4 * u[1] - u[2]) / (2 * h)     
    d[-1] = (u[-3] - 4 * u[-2] + 3 * u[-1]) / (2 * h)     
    # 内部点使用中心差分     
    d[1:-1] = (u[2:] - u[:-2]) / (2 * h)      
    
    u_tensor = torch.tensor(u, dtype=torch.float32)     
    d_tensor = torch.tensor(d, dtype=torch.float32)      
    
    return u_tensor, d_tensor, t# 模型训练 

以“受迫振动方程”这一测试框架为例，force_oscillator函数中刻画了该场景下的微分方程规律：

1
2
3
4
5

def forced_oscillator(t, y):
    x1, x2 = y
    dx1dt = x2
    dx2dt = -np.cos(t) * x1 - x2 + t / 50
    return [dx1dt, dx2dt]

生成的无噪声数据如下图所示：

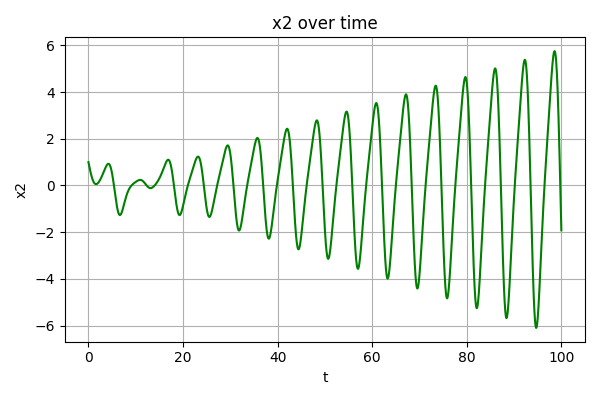
神经网络训练

根据上述算法理论部分列出的训练流程框架，适用数据（u，d）对神经网络进行训练，训练后得到的函数f_NN即为对函数f的近似。

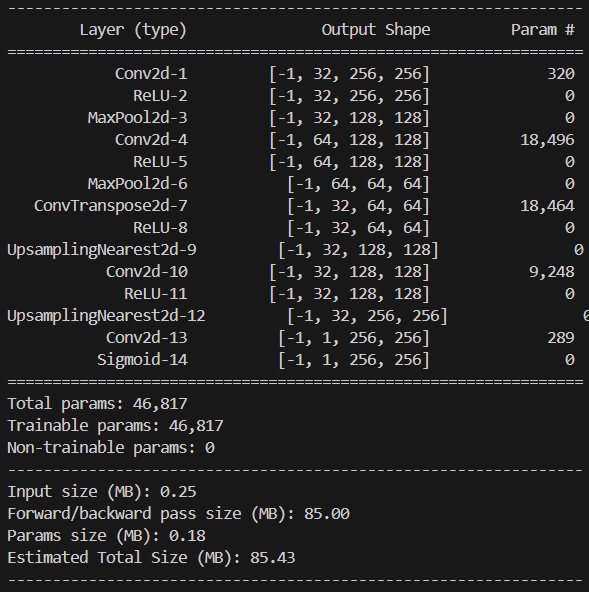
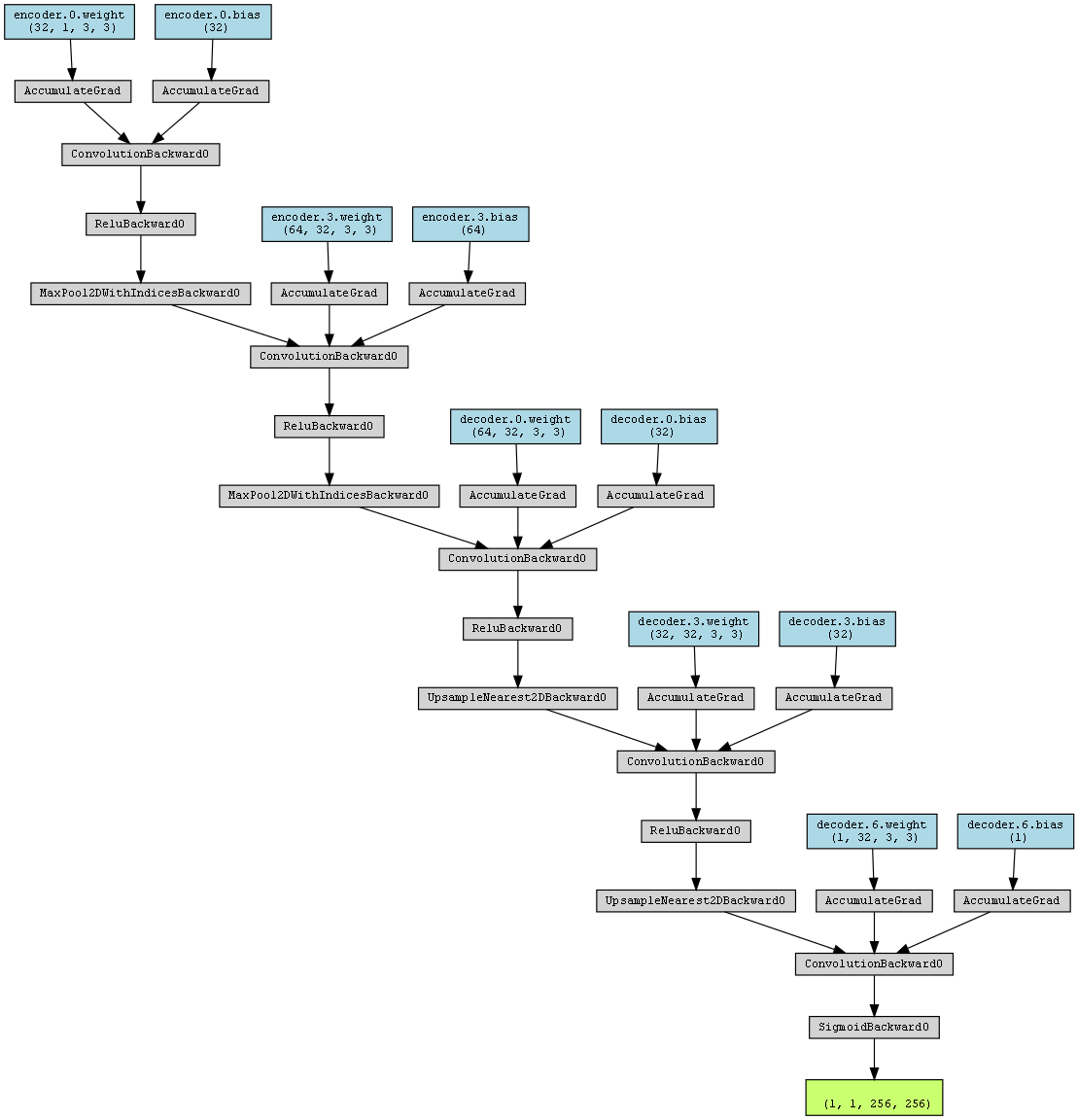
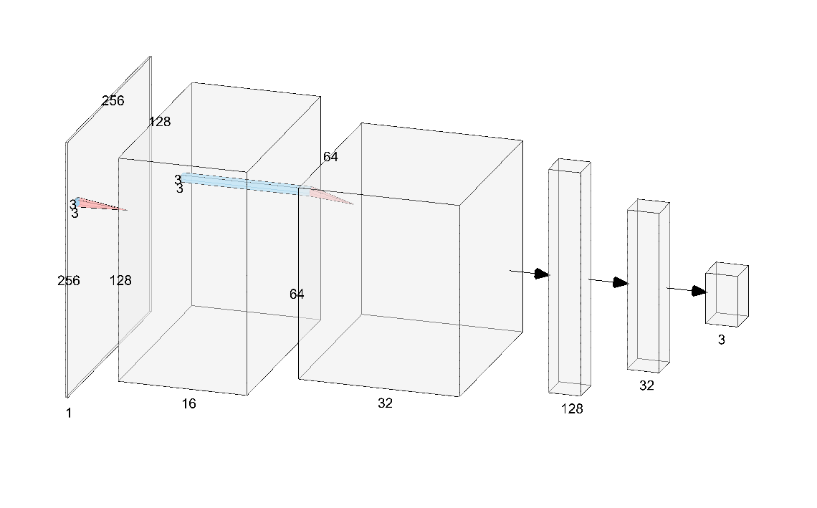
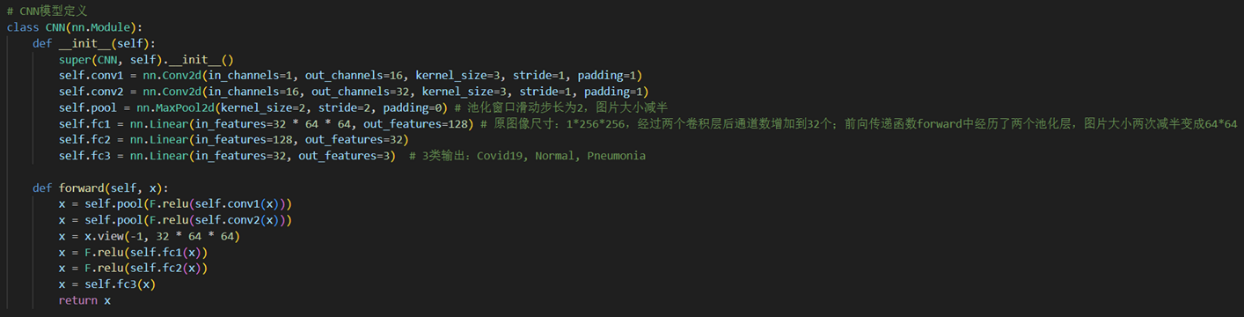
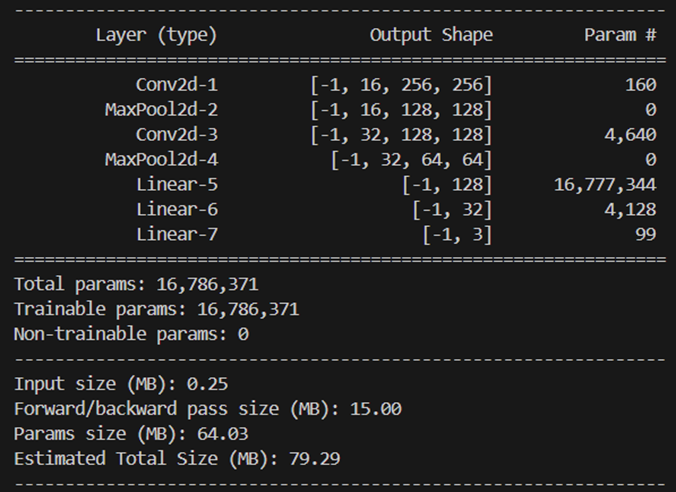
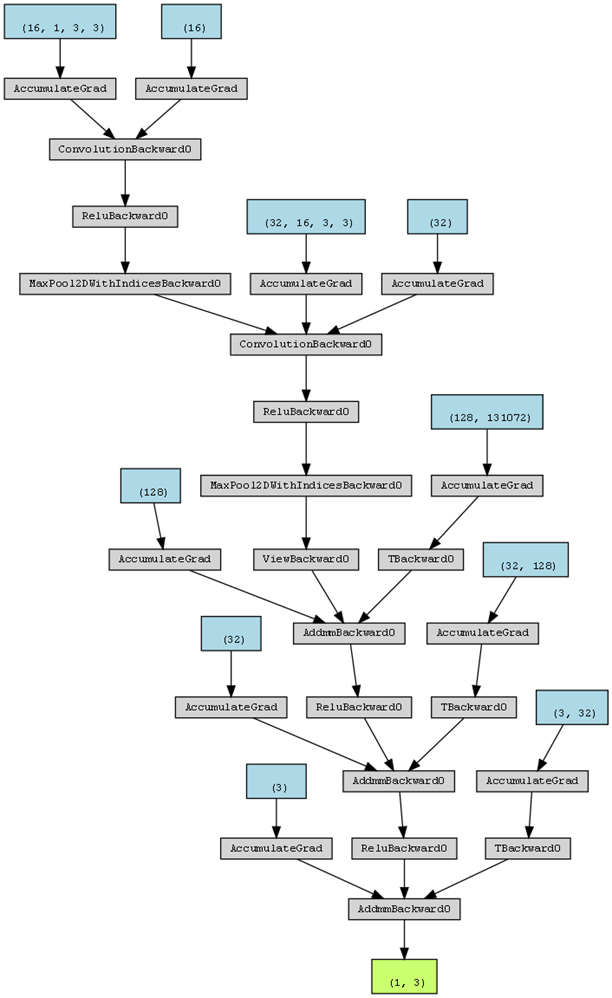
关于神经网络的结构与参数，本项目中所使用的神经网络结构均相同（后续不再赘述），均包含4个隐藏层，每层128个神经元，激活函数为tanh，Python中基于pytorch框架对神经网络架构的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import torch.nn as nn

class ODEApproximator(nn.Module):
    def __init__(self, input_dim=3, hidden_dim=128, output_dim=3):
        super(ODEApproximator, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, output_dim)
        )

    def forward(self, x):
        return self.net(x)

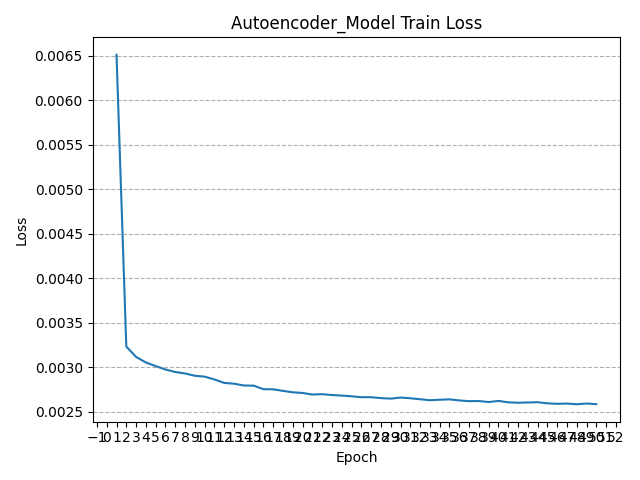
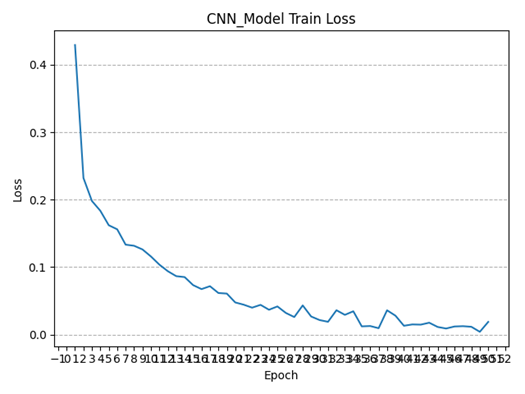
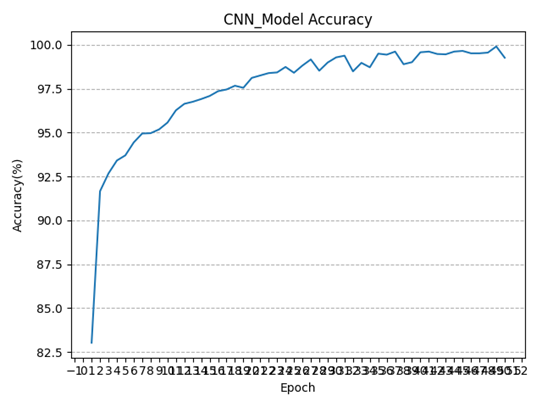
训练过程中实时记录了每一个epoch的损失函数值，下图分别绘制了改进前后的多步神经网络在无噪声数据集上训练过程中损失函数值的变化情况（总Epoch=100），可以看到损失函数均呈收敛态势，且改进后的多步神经网络收敛更快：

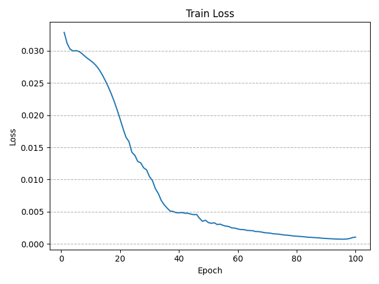
效果检验

为定量地比较改进前后的多步神经网络的泛化性能与鲁棒性，采取如下的实验步骤进行训练后模型的效果检验：

1. 用训练得到的函数f_NN解方程得到数值解u_NN^(n) ,观察近似效果，计算均方误差mse_x 和平均绝对误差mae_x并与多步神经网络作比较；
2. 用数值解u^(n)代入训练得到的函数f_NN得到的导数的近似值d_NN^(n)，将u^(n)代入给定的常微分方程中的 f 得到导数的真实值d^(n),计算均方误差mse_f和平均绝对误差mae_f并与多步神经网络作比较。

其中用于比较性能的指标均方误差mse和平均绝对误差mae的定义式如下所示：
$$
mse_{x}=\frac{1}{ND}\sum_{n=1}^{N}\left|u_{NN}^{(n)}-u^{(n)}\right|_{2}^{2}
$$

$$
mse_{f}=\frac{1}{ND}\sum_{n=1}^{N}\left|d_{NN}^{(n)}-d^{(n)}\right|_{2}^{2}
$$

$$
mae_{x}=\frac{1}{ND}\sum_{n=1}^{N}\left|u_{NN}^{(n)}-u^{(n)}\right|_{1}
$$

$$
mae_{f}=\frac{1}{ND}\sum_{n=1}^{N}\left|d_{NN}^{(n)}-d^{(n)}\right|_{1}
$$

Python中将利用训练好的模型进行预测的过程封装成函数predict_u，指标计算直接调用scikit-learn函数库中的相关函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def rhs(t, u_np):      
    """用于 solve_ivp：输入 u = [x1, x2, t] 输出 du/dt"""      
    u_tensor = torch.tensor(u_np, dtype=torch.float32).unsqueeze(0).to(device)      
    with torch.no_grad():          
        du_dt = model(u_tensor).squeeze().cpu().numpy()      
    return du_dt    

def predict_u(u_tensor):      
    # 初始条件与时间点一致     
    u0 = u_tensor[0].cpu().numpy()  # [x1, x2, t]    
    t_span = (0, 100)  
    t_eval = np.arange(0, 100 + 0.05, 0.05)    
    
    sol_nn = solve_ivp(rhs, t_span, u0, t_eval=t_eval)   
    return sol_nn.y.T  # shape: [N, 3]

在“受迫振动方程”这一测试案例中，基于训练轮数Epoch=50的模型，运行以上检验流程，得到如下检验指标数据：

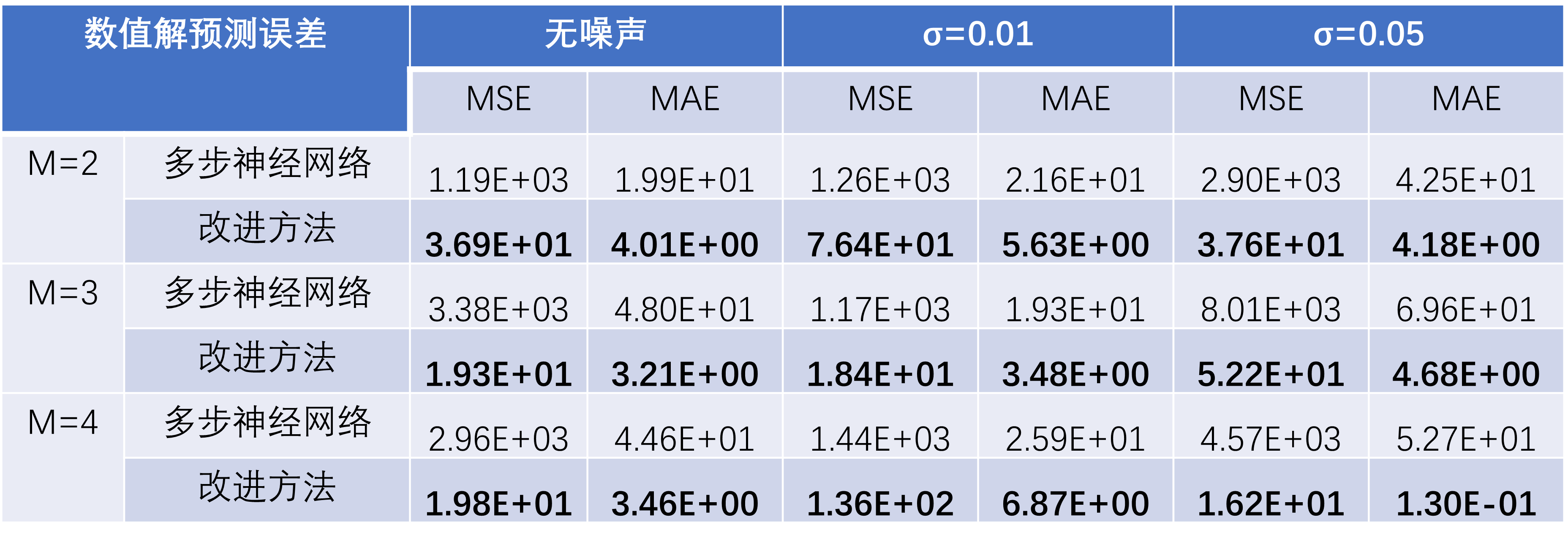
可以看到，随着噪声强度增加，两种方法的误差均增大，但改进方法对数值解的预测误差在各种情况下均小于多步神经网络。

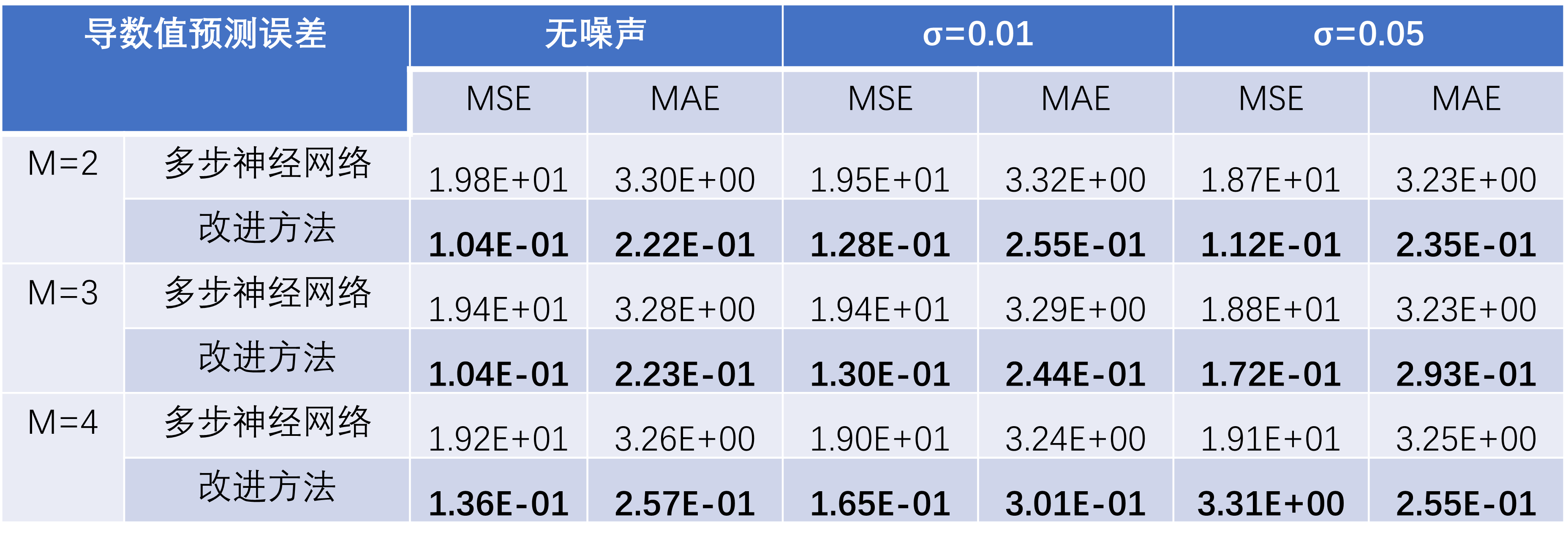
可以看到，当数据无噪声时，本文提出的改进方法对于受迫振动方程的近似效果强于多步神经网络;随着噪声强度的增加，多步神经网络的误差大幅增加，而改进的方法的误差一直保持较小且始终强于多步神经网络。

除此之外，针对在无噪声数据集上训练轮数分别为Epoch=100和Epoch=500时的模型，将其作为微分方程中的f用于预测数据的生成，效果分别如下图所示：

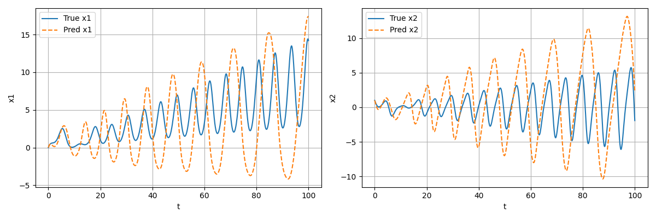
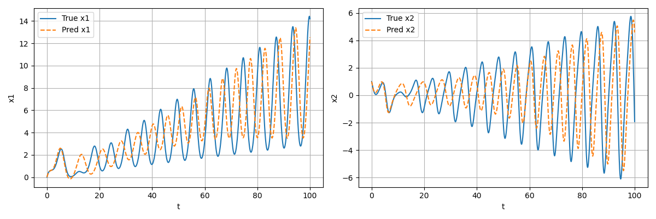
可以看到，随着训练轮数的增加，模型对于实际微分方程的拟合效果越来越好，生成的预测数据也越来越接近用于训练的真实数据；事实上，从理论上讲，大概在训练轮数Epoch达到10^4数量级时才会有较为精准的拟合效果，本项目由于用于训练的计算资源有限，仅进行了最大训练轮数为1000的测试。在后续的结果分析部分，将直接采用高训练轮数下的精确结果进行展示。

数值实验结果分析

非自治常微分方程

受迫振动方程——Adams-Moulton法

受迫振动方程(Forced Oscillator)是描述一个振动系统在外界力的作用下进行振动的方程。这个方程可以用来研究各种物理系统中的振动现象，例如弹簧振子、摆锤、电路振荡等。受迫振动方程的核心思想是将外界力引入方程中，以描述振动系统在外界激励下的行为。受迫振动方程的研究对于科学、工程和技术领域具有重要意义。它不仅有助于我们深入理解振动现象的本质和规律，还为我们设计和优化振动控制系统、减振装置等提供了理论基础。同时，它在电子设备、结构工程、交通运输等方面也有广泛的应用。

实验使用的受迫振动方程如下：
$$
\begin{aligned}&\frac{dx_1}{dt}=x_2,\&\frac{dx_2}{dt}=-cosy\cdot x_1-x_2+\frac{y}{50},\&\frac{dy}{dt}=1\end{aligned}
$$
使用[0,1,0]T作为初值，生成从t=0到t=100，间隔h=0.05的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

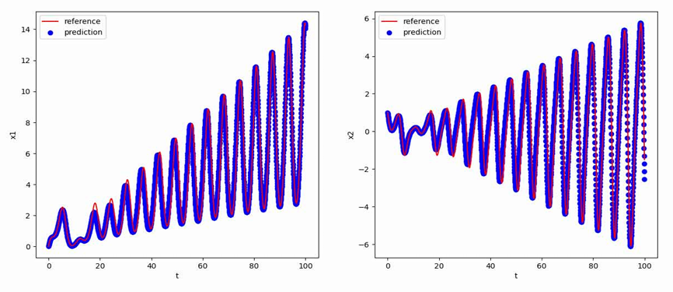
线性标量方程——Adams-Bashforth法

线性标量方程(Linear Scalar Equation)是一种描述某个未知函数与其导数之间的关系的方程，其中未知函数的导数的最高次数为1。线性标量方程是微分方程中的一类重要问题，它在数学物理等领域中有广泛应用。线性标量方程的研究对于数学、物理学和工程学等领域具有重要意义。它可以用来描述动力学系统的行为、传热和传质过程、量子力学中的波函数演化等。通过分析和求解线性标量方程，可以深入理解系统的特征、稳定性、渐近行为等，为问题的模拟、控制和优化提供理论基础。在现代科学和工程中，线性标量方程的研究得到了进一步推广和延伸。例如，非线性标量方程、偏微分方程等是线性标量方程的扩展和推广，它们更好地描述了一些复杂的物理现象和现实问题。

实验使用的线性标量方程如下：
$$
\frac{dx_1}{dt}=-x_1(sin4y+1)+cos\frac{y^2}{1000},
$$

$$
\frac{dy}{dt}=1
$$

使用[2,0]T作为初值，生成从t=0到t=20，间隔h=0.05的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

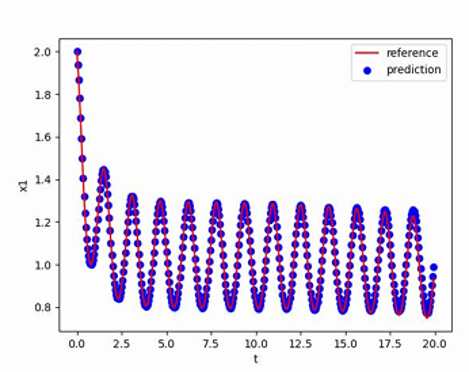
食饵-捕食者模型方程——后向微分公式法

食饵-捕食者模型(Predator-prey Model)是生态学中研究食物链和生物群落动力学的重要模型之一，描述了食物链中食饵(被捕食者)和捕食者之间的相互作用关系。这种模型的研究对于我们理解生态系统的稳定性、物种相互作用以及生态系统中物种数量的变化具有重要意义。通过食饵-捕食者模型，我们可以研究食饵与捕食者之间的数量关系以及它们之间的相互作用。一般来说，食饵的数量被认为是捕食者的食物来源，并且捕食者的数量受到食饵的供给和捕食行为的影响。该模型通常描述了食饵数量随时间的变化，以及捕食者数量随时间的变化。食饵-捕食者模型的研究对于生态学、环境保护和资源管理等领域具有重要意义。通过该模型，我们可以深入了解生态系统中物种数量的变化规律，从而预测物种灭绝和生态系统崩溃的风险，以及寻找保护和管理生物多样性的方法。

实验使用的食饵-捕食者模型方程如下：
$$
\begin{aligned}&\frac{dx_1}{dt}=x_1-x_1\cdot x_2+sin\frac{y}{2}+cosy+2,\&\frac{dx_2}{dt}=x_1\cdot x_2-x_2,\&\frac{dy}{dt}=1\end{aligned}
$$
使用[3,3,0]T作为初值，生成从t=0到t=50，间隔h=0.05的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

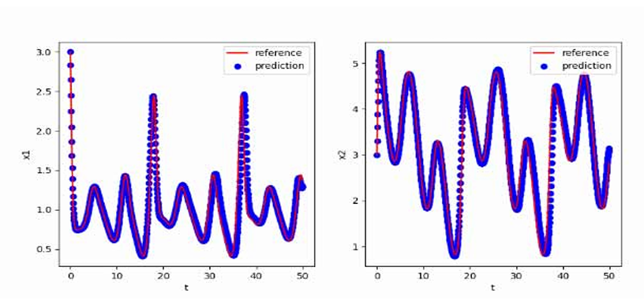
自治常微分方程

线性常微分方程——Adams-Moulton法

线性常微分方程(Linear ODEs)是微分方程中的一类重要问题，它描述了未知函数及其导数之间的线性关系。线性常微分方程的研究对于数学、物理学和工程学等领域具有重要意义。它们出现在物理学中许多基础问题的数学描述中，例如弹簧振动、电路分析、传热过程等。在工程学中，线性常微分方程也广泛应用于控制系统的建模和分析。随着科学技术的发展，研究者提出了各种各样的数值方法和近似方法，以求解复杂的线性常微分方程。这些方法包括欧拉方法、龙格-库塔方法、有限差分方法、变分法等，它们为实际问题的求解提供了有效的数值工具。随着对非线性动力学系统的研究和认识的深入，研究者们开始将非线性常微分方程引入到线性常微分方程中，以描述更为复杂的现象和现实问题。

实验使用的线性常微分方程如下：
$$
\frac{dx_1}{dt}=x_1-4x_2,
$$

$$
\frac{dx_2}{dt}=4x_1-7x_2
$$

使用[0,-1]T作为初值，生成从t=0到t=10，间隔h=0.01的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

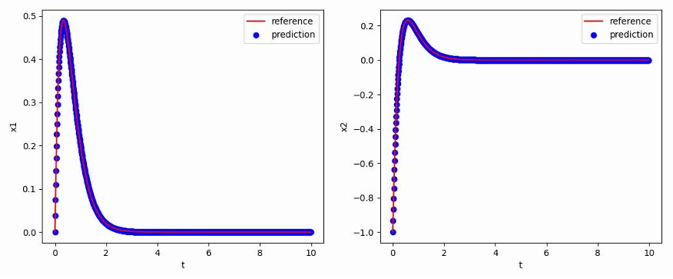
阻尼三次振子方程——Adams-Bashforth法

阻尼三次振子(Damped Cubic Oscillator)是一种物理系统，它描述了受到阻尼力和弹力作用的振动系统。阻尼指的是系统中存在能量损耗的因素，如摩擦力，它会导致振动的逐渐减弱；三次振子表示系统的势能函数是一个三次函数，它具有非线性的特性。阻尼三次振子最早出现在振动力学和非线性动力学的研究中。对于振动系统的研究是物理学、工程学和应用数学等领域的重要课题之一。阻尼三次振子的研究对于理解和预测复杂动力学系统的行为具有重要意义。通过分析阻尼三次振子的运动规律和稳定性，我们可以深入了解非线性振动系统的动力学特性，例如振动的周期性、混沌行为等。这些研究也为控制系统、电子电路、力学系统等领域的工程应用提供了参考和启示。

实验使用的阻尼三次振子方程如下：
$$
\frac{dx_1}{dt}=-0.1x_1^3+2x_2^3,
$$

$$
\frac{dx_2}{dt}=-2x_1^3-0.1x_2^3
$$

使用[1,1]T作为初值，生成从t=0到t=25，间隔h=0.01的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

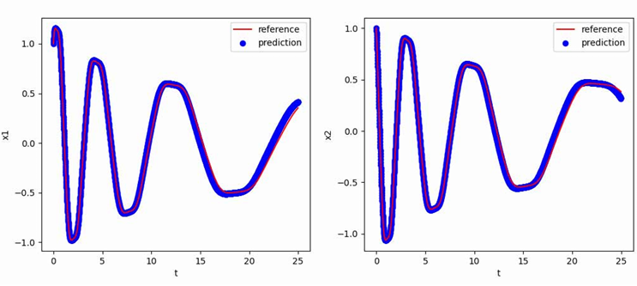
阻尼简谐摆方程——后向微分公式法

阻尼简谐摆(Damped Pendulum)是一个经典力学中的物理系统，它由一个具有质量的物体通过一根轻质绳或杆与一个固定支点相连接组成。阻尼简谐摆在受到重力作用下，沿着一条弧线进行周期性振动。阻尼简谐摆的研究对于理解和预测振动系统的行为具有重要意义。通过分析阻尼简谐摆的运动规律和稳定性，我们可以深入了解振动系统在存在阻尼时的响应特性，例如振动的振幅、频率等。这些研究不仅在理论物理学中具有重要意义，也为工程学中的控制系统、机械振动和结构动力学等领域的应用提供了基础。

实验使用的阻尼简谐摆方程如下：
$$
\begin{aligned}&\frac{dx_1}{dt}=x_2,\&\frac{dx_2}{dt}=-\alpha x_2-\beta\sin x_1,\&\alpha=0.2,\beta=8.91\end{aligned}
$$
使用[-1.193,-3.876]T作为初值，生成从t=0到t=20，间隔h=0.01的数据作为训练集，最终得到的多步神经网络对常微分方程的反演效果如下图所示，其中红色曲线是原方程数值解的曲线，蓝色点是用无噪声数据训练的函数f_NN代替f得到的数值解:

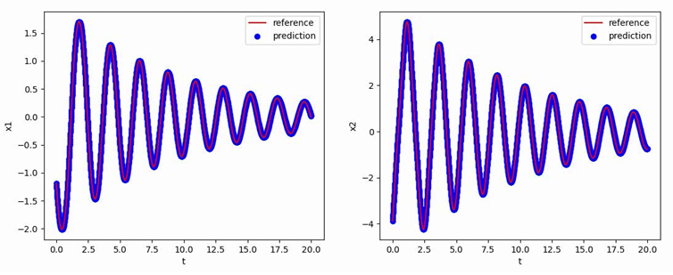
研究结论与创新

研究结论

本项目针对常微分方程的反演问题提出了一种基于多步神经网络改进的常微分方程反演算法，旨在从数据中提取内含的常微分方程。通过将导数数据融入训练数据，我们改进了多步神经网络的数据集，并优化了神经网络的损失函数，以提高模型的准确性和泛化能力。经过训练，改进的神经网络成功拟合原方程中的函数，实现了对非自治常微分方程的反演。我们还推导并讨论了改进算法的误差界。我们进一步将改进的算法应用于自治常微分方程反演，通过训练网络拟合原方程函数，拓展了算法在自治常微分方程反演中的适用性。

本项目通过实验以非自治常微分方程中的受迫振动方程、线性标量方程和食饵-捕食者模型方程，以及自治常微分方程中的线性常微分方程、阻尼三次振子方程和阻尼简谐摆方程为例，展示了算法的有效性。在实验中，我们添加了不同强度的噪声，并利用改进算法对常微分方程进行反演。实验结果表明，改进方法在大多数情况下优于多步神经网络，在处理有噪声数据时表现更为出色。这些结果充分验证了本文提出的方法在反演问题中的可行性和优越性。

研究方法创新性

传统方法通常利用多步神经网络来处理常微分方程的反演问题，主要集中在处理自治常微分方程，对于非自治常微分方程的反演效果不尽理想，特别是在使用带有噪声数据进行训练时表现不佳。本研究首次将研究重点聚焦于非自治常微分方程的反演，通过将非自治方程转化为自治方程的形式，提出了一种新的研究思路。针对带有噪声数据的方程反演问题，采用了改进损失函数的方法以提升算法的鲁棒性。此外，将这种新方法扩展应用于自治常微分方程的反演问题，结果显示其反演效果明显优于多步神经网络。这一新思路对解决常微分方程反演问题带来了一种新的方法。

参考文献

[1] 王开荣,杨大地编著.应用数值分析[M].高等教育出版社,2010.

[2] 付长铠.常微分方程反演的机器学习方法研究[D].长春工业大学,2024.

[3] Raissi M, Perdikaris P, Karniadakis G E. Multistep neural networks for data-driven discovery of nonlinear dynamical systems[J]. arXiv preprint arXiv:1801.01236, 2018.

[4] 李航. 统计学习方法[M]. 第二版. 北京：清华大学出版社, 2019.

[5] 陈新海, 刘杰, 万仟, 等. 一种改进的基于深度神经网络的偏微分方程求解方法[J]. 计算机工程与科学, 2022, 44(11): 1932-1940.

1 项目背景与研究意义

1.1 项目背景

肺炎作为一种常见的呼吸系统疾病，对人类健康构成了长期威胁，特别是随着COVID-19新冠肺炎疫情的全球爆发，其公共健康影响更为显著。COVID-19肺炎具有传播速度快、感染范围广、诊断难度大的特点，对全球医疗系统和社会经济产生了深远影响。特别是在疫情高峰期，医疗资源的短缺和诊断效率的瓶颈，进一步突显了快速、准确诊断工具的重要性。

传统肺炎诊断方法主要依赖医生对胸部X光片或CT图像的人工分析，既耗时又容易受到经验和疲劳的影响，尤其在COVID-19疫情期间，大量影像数据的涌现使得人工诊断难以满足需求。与此同时，COVID-19的影像表现与其他类型肺炎的重叠性增加了诊断的复杂性，这进一步加剧了对智能化诊断系统的需求。

随着人工智能技术的快速发展，深度学习为医疗影像分析带来了全新的解决方案。卷积神经网络（Convolutional Neural Network, CNN）凭借其强大的图像特征提取能力，在自动化诊断中展现了巨大潜力。同时，由于不同医疗机构的CT扫描设备性能差异显著，特别是在医疗资源较为匮乏的地区，CT影像常常受到设备老化、分辨率低或操作不规范等因素的影响，图像质量参差不齐，这不仅增加了诊断的复杂性，还对自动化系统的鲁棒性提出了更高要求；而自编码器（Autoencoder）作为一种有效的降噪工具，为医疗影像数据预处理提供了重要支持。通过自编码器的引入，可以有效消除图像中的噪声干扰，减少不同设备间的成像差异，为后续的分类和识别模型提供高质量的输入数据。因此，本项目提出结合自编码器和卷积神经网络的深度学习框架，开发一套针对肺炎（包括COVID-19）CT影像识别的智能诊断系统。

1.2 研究意义

本项目以新型冠状病毒肺炎为切入点，面向未来医学智能化需求，开发的诊断系统不仅能够应对当下疫情挑战，还具有推广至其他医学影像诊断场景的潜力，从而为全球公共健康事业的发展提供有力支持。

面向新冠肺炎疫情期间大规模肺部影像数据的快速诊断需求，本系统依托深度学习技术，有效提升了诊断效率，为疫情防控和患者管理提供重要的技术支持。通过先进的模型算法，系统能够精准识别肺部CT影像中的病变特征，减少人为误差，确保诊断结果的准确性和一致性，大幅降低不同医疗机构和医生之间的诊断差异，避免误诊和漏诊风险，从而更好地保障患者安全。

针对基层医院或偏远地区医疗资源匮乏的现状，本系统可作为一种可靠的辅助诊断工具，为医生提供科学的决策支持，帮助缓解诊断能力不足带来的压力。其高效的处理能力不仅提高了基层医疗服务水平，也为疫情防控的全面推进提供了技术保障，为应对紧急医疗需求的地区解决实际困难。

此外，本系统在高效处理和分析海量肺部CT影像数据的基础上，还为研究新冠肺炎的病理特征及流行规律提供了宝贵的数据支持。这些分析结果可进一步应用于疫情传播趋势预测和公共卫生政策制定，为疫情防控策略的科学性和有效性奠定了坚实基础。

同时，本系统也为患者病情的动态管理提供了重要帮助。通过智能分析新冠肺炎影像特征的变化趋势，系统能够为临床医生提供精确的病情评估建议，有助于及时调整治疗方案。这种基于影像数据的技术支持，不仅提高了患者管理的科学性和有效性，还为医疗资源的合理分配提供了重要依据，进一步推动了疫情防控工作的高效开展。

2 数据集获取与预处理

2.1 数据集介绍

本项目使用的肺部X-光片数据集从Kaggle网站（链接：https://www.kaggle.com/datasets/alsaniipe/chest-x-ray-image）获取，共分为三类标签：新冠肺炎COVID19、正常NORMAL和普通肺炎PNEUMONIA，该数据集已经事先划分好了训练集与测试集。此外，为测试模型对于不同质量CT影像的识别精度，还对测试集中的部分图像使用高斯噪声进行扰动，以模拟实际CT扫描的成像质量差异。

数据分布如下表所示：

表2.1：数据集数据分布情况

2.2 编程环境搭建

本项目中所有的代码编写与运行均是在配备NVIDIA GeForce RTX 3060显卡、16GB运行内存、12th Gen Inter(R) Core(TM) i7-12700@2.10GHz处理器与Microsoft Windows 11操作系统的工作站上使用Python编程语言完成的。

软件环境方面，采用Conda进行环境管理，在控制台中通过命令”conda create -n covid python=3.12”创建虚拟环境，并在激活环境后使用pip install命令依次安装所需的各种依赖库；全部安装并测试完成后，通过命令”pip freeze >
requirements.txt”将虚拟环境中安装的所有依赖库及对应版本写入文件requirements.txt，后续移植时可在新的运行环境中运行命令”pip install -r requirements.txt”完成环境的一键配置。

值得注意的是，在PyTorch（包括torch、torchvision与torchaudio库）安装时需要根据自己电脑使用的CUDA版本（使用CPU则直接在命令行中使用pip install安装即可）在PyTorch官网中找到对应的安装命令进行安装。我使用的CUDA版本为12.6，安装命令的选取如下图所示：

下面对于项目中使用到的主要依赖库进行简要介绍：

其中，plt用于绘图，nn中包含了用于构建神经网络的隐藏层（全连接层、卷积层等），F中包含了各种激活函数（ReLu、Sigmoid等），DataLoader用于在训练时加载数据，datasets和transforms用于读取和处理数据集，tqdm用于进度条可视化，torchmetrics用于模型精度的测试，torchviz和torchsummary用于以图形与文字的方式描述模型架构概况。

2.3 图像数据读取

torch对于一些常用的数据集做了封装，可以直接调用，例如datasets.MNIST()。但此处我们使用的是本地的图片数据，可以使用ImageFolder将一个文件夹下的图片读取成数据集并完成数据增强工作。在读取完数据集后，还需要定义DataLoader用于加载数据为可分批次（batch）读取的迭代器以供后续使用。为使得代码更加简洁，将上述的数据读取与加载过程为封装在getDataLoader函数中，并在主函数中通过指定不同的目录加载训练集、测试集或是含噪声测试集。

可以看到，其中构建了数据增强器transform，在读取数据时进行相应处理：

• Grayscale: 指以灰度图的形式读取。

• Resize: 由于图像尺寸各不相同，在训练前需将它们重塑成相同尺寸256*256。

• ToTensor: 将图片格式转换成张量形式，torch的计算以张量的形式进行。

除此之外，在构建数据加载器时需要指定一个批次（batch）中的图片数据数量batch_size，在模型训练时训练批次大小TRAIN_BATCH_SIZE也是会影响最终模型性能的重要超参数之一。在训练过程中，设定TRAIN_BATCH_SIZE为32，而在测试过程中，为提高测试效率，将TEST_BATCH_SIZE设置为66并对函数进行对应修改。

2.4 叠加噪声函数

不论是构建噪声测试集，还是在利用无噪声的训练集进行训练时，都需要手动添加噪声，故编写add_noise函数，默认的噪声强度为0.5，并在添加噪声后进行归一化以确保图像值位于[0,1]范围内。

3 模型构建与网络训练

3.1 整体模型框架

整体模型框架由两个核心部分组成，分别是用于去噪的数据预处理模块和负责分类的卷积神经网络（CNN）。去噪模块采用自编码器（Autoencoder）的架构，专注于从输入数据中去除噪声，以提升后续分类的准确性；分类模块基于卷积神经网络，其强大的特征提取和模式识别能力使其成为分类任务的理想选择。

两个模块相辅相成，通过有效的数据处理和特征提取，确保模型能够在噪声干扰较大的环境中实现高精度分类。噪声数据首先经过自编码器处理，生成质量优化的特征表示，然后被CNN接收并完成分类任务。这一整体框架设计非常适合肺炎图像识别任务，通过结合去噪和分类两大模块的优势，模型不仅能够有效提高数据质量，还能充分挖掘数据中的有用特征，从而能够在复杂的医学影像处理中表现出卓越的鲁棒性和准确性，满足肺炎诊断的实际需求。

3.2 自编码器

自编码器模型用于处理输入数据中的噪声问题，提升后续分类的准确性。其核心思想是通过编码器将输入数据压缩至低维潜在表示（latent representation），再由解码器将其还原至去噪后的重构数据，从而实现降噪效果。

3.2.1 网络结构设计

自编码器网络结构由编码器encoder与解码器decoder组成：

• 编码器由两层卷积（Conv2d）和两次池化（MaxPool2d）操作组成，用于提取特征；

• 解码器通过两次反卷积（ConvTranspose2d）和两次上采样（UpsamplingNearest2d）逐步恢复图像尺寸到原始大小；

• 最后使用Sigmoid激活函数将输出值限制在[0,1]区间。

模型定义代码如下：

模型继承自nn.Module类，在__init__()函数中定义模型的结构，在forward()函数中定义模型的前向传播过程。

通过调用torchviz和torchsummary库，可以输出该模型结构的基本信息：

3.2.2 模型训练

基本的训练流程集成在函数train_autoencoder_process中，如下图所示：

其中指定优化器optimizer为Adam，损失函数为均方误差MSE，并使用超参数：训练轮数Epochs=50、学习率lr=0.001。每轮（Epoch）训练中均需要以多个batch的形式遍历训练集中的所有数据，并在每个batch后对模型进行更新，具体而言每次更新均需执行如下操作：

• 从加载器中获取输入数据

• 使用add_noise函数对干净图像加噪

• 将加噪后图像输入自编码器模型并计算模型输出

• 根据模型输出和标签计算损失Loss

• 清空梯度

• 反向传播

• 更新模型

值得注意的是，由于用于训练的图像数据没有噪声，因此训练时首先需要对输入的图像进行加噪处理，再输入自编码器模型进行训练。

训练过程中还利用tqdm进度条函数对训练进程进行可视化，并在每轮训练完成后打印出当轮训练过程中模型的平均损失：

在训练过程中，将每轮训练的平均损失存储在列表中，并在训练结束后将平均损失的变化过程以图像形式呈现：

可以看到，经过多轮训练，模型的损失函数值在不断减小且逐渐趋近于0，这意味着该自编码器的模型训练过程是收敛的，模型具有较稳定的工作性能。

3.3 卷积神经网络

卷积神经网络负责从图像中提取多层次的空间特征，通过逐步减少图像尺寸和增加特征通道来捕捉关键信息，从而实现去噪后肺部CT图像的分类功能。CNN以其强大的特征提取能力，能够有效处理图像的局部依赖性和空间不变性，高效处理结构化数据（如图像、时序数据）。模型简单且高效，具有较强的泛化能力，适合处理小规模数据集的图像分类问题。

3.3.1 网络结构设计

卷积神经网络结构（如上图，通过NN-SVG工具绘制）由两层卷积层（Conv2d）和池化层（MaxPool2d）组成，激活函数均选用ReLU，逐步提取特征并将输入图像的尺寸从原始大小减小到64×64。卷积后的特征图展平后通过三个全连接层（Linear），分别将特征维度从32×64×64降至128，再降至32，最后输出3个类别（Covid19、Normal、Pneumonia）的预测结果。

模型定义代码如下：

模型继承自nn.Module类，在__init__()函数中定义模型的结构，在forward()函数中定义模型的前向传播过程。

通过调用torchviz和torchsummary库，可以输出该模型结构的基本信息：

3.3.2 模型训练

基本的训练流程集成在函数train_cnn_process中，如下图所示：

其中指定优化器optimizer为Adam，损失函数为交叉熵损失CrossEntropy，并使用超参数：训练轮数Epochs=50、学习率lr=0.001。每轮（Epoch）训练中均需要以多个batch的形式遍历训练集中的所有数据，并在每个batch后对模型进行更新，具体而言每次更新均需执行如下操作：

• 从加载器中获取输入数据

• 使用add_noise函数对干净图像加噪

• 将加噪后图像输入训练好的自编码器模型trained_autoencoder_model

• 将经过自编码器去噪后的图像输入CNN模型并计算模型输出

• 根据模型输出和标签计算损失Loss

• 清空梯度

• 反向传播

• 更新模型

值得注意的是，由于用于训练的图像数据没有噪声，为与实际的输入情况一致，首先需要对输入的图像进行加噪处理，再利用训练好的自编码器模型进行降噪（为了不在更新CNN的同时更新自编码器，这一步不需要产生梯度），才能输入CNN分类模型进行训练。

训练过程中还利用tqdm进度条函数对训练进程进行可视化，并在每轮训练完成后打印出当轮训练过程中模型的平均损失与在训练集上的测试精度：

在训练过程中，将每轮训练的平均损失与模型在训练集上的测试精度存储在列表中，并在训练结束后将两者的变化过程以图像形式呈现：

可以看到，经过多轮训练，模型的损失函数值在不断减小且逐渐趋近于0，这意味着该自编码器的模型训练过程是收敛的，模型具有较稳定的工作性能；同时随着训练轮数增加，模型在训练集上的精度也逐渐增高（波动上升），在模型训练完成时，卷积神经网络在训练集上的分类精度已经可以达到99.59%（一度达到99.90%），接近百分之百，说明模型的分类能力较好。

4 模型测试及应用

4.1 自编码器降噪效果

在自编码器模型的训练过程中，每隔10轮对模型参数进行了一次存档；在测试过程中，分别使用训练轮数为10、20、30、40、50的自编码器模型对于加噪后的模型进行降噪处理，效果如下图所示：

通过对比不同训练轮数的自编码器模型降噪效果可以发现，随着训练轮数的增加，自编码器模型的降噪效果在逐渐提升，但在Epoch到达30之后，训练带来的降噪效果提升就不如先前显著了。尽管由于较大的噪声强度（0.5）导致降噪后的图像仍然比较模糊，但通过肉眼还是能粗略观察处肺部骨骼的轮廓等特征，后续实验也证明了卷积神经网络确实可以从这样清晰度的图像中提取相应的特征来进行分类，该自编码器模型的设计有效。

4.2 卷积神经网络分类精度

在卷积神经网络的分类精度上，训练过程中已经实时对于每一轮训练后的模型在训练集上进行了精度测试（3.2.2节中已有提及），而在测试集上，可以编写与训练过程类似的代码利用torchmetrics库对模型分类精度进行测试，只是不会更新模型，代码如下：

可以看到，由于我们的测试集分为含噪声和不含噪声两类，因此编写了不同的函数对模型分类精度进行测试。两个函数的主要差别就在于，由于含噪声测试集是已经加噪的图片（噪声与手动通过add_noise函数添加的不同），因此在含噪声测试集的测试代码中不必再次手动添加噪声，而是直接将图像输入自编码器降噪后再输入CNN分类模型中进行分类；而对于不含噪声的测试集而言，为模拟与训练集同样的处理流程，会先进行手动加噪再通过自编码器降噪之后才输入CNN分类模型中进行分类。

运行测试代码后，得到模型在含噪测试集上的分类精度为96.97%，在不含噪声的测试集上的分类精度为94.57%，在两个测试集上的分类精度水平均较高，说明该模型具有良好的分类效果。

4.3 模型应用：基于CT影像的肺炎诊断Web服务

通过对比多组超参数的模型降噪与分类效果，最终选定如下的超参数：

• 训练轮数Epochs=50；

• 学习率LR=0.001；

• 训练批次大小Train_Batch_Size=32。

选定参数后，将整体代码抽离为model.py（包含模型定义类代码），run.py（服务端代码）和train.py（训练函数），并将模型部署到实际应用中，使用Flask作为服务端，以Web形式用户提供操作接口以上传图片进行诊断。由于主要功能是提供接口，故网页只做了很简易的一个index.html，给用户提供上传图片的按钮，并在用户上传有噪声的CT影像后返回诊断结果及去噪后的图像。除此之外，还将挂载在本地端口上的Web通过内网穿透映射到公网，以供实时访问。

网页初始界面如下图所示：

接下来分别测试当输入COVID19、NORMAL和PNEUMONIA三个组别的图片，模型能否正确判断：

可以发现，模型在大多数情况下可以正确识别图像来源，但也会出现错误识别的情况，这和Test 集上的Accuracy相符合；此外，在测试时还注意到，模型识别结果偶尔会出现不稳定的现象，即输入同一张图像有时识别为某一类别，有时又会识别为另一类别，这是由模型内部部分随机参数导致的，这也反映了模型在一些模棱两可的情况下（两类别概率接近）做出判断时的不稳定性。在实际应用中，为尽可能减少误诊对于患者带来的各方面影响，还需要采取更多优化措施提升模型性能，并对模型在模棱两可的情况下做出的判断进行合理的限制。

5 总结与展望

本项目全部代码（不包含数据集）已上传至Github仓库，仓库URL地址：https://github.com/Asgard-Tim/Pneumonia-Image-Recognition

5.1 项目总结

本项目基于深度学习技术，结合自编码器和卷积神经网络，开发了一套智能诊断系统，用于快速、高效地识别肺部的CT影像并判断该患者是否患有肺炎（包括COVID-19）。自编码器模块有效去除了噪声，提升了图像质量，而卷积神经网络以其强大的特征提取能力，实现了高精度的分类。本项目在数据预处理、模型设计、网络训练及测试等环节中均采用了创新性的技术方案，最终实现了在含噪声测试集上96.97%和在无噪声测试集上94.57%的分类精度，表现出了较高的鲁棒性和实用价值。同时，系统已通过Flask框架部署为Web服务，能够实时接收CT影像并给出诊断结果，为疫情期间大规模影像数据的快速诊断及基层医疗资源匮乏地区的医疗支持提供了重要的技术保障。

5.2 课程收获与反思

本次选修《智能图像处理》这门课程确实让我学到了很多东西，其实自己之前也自己看过一些机器学习方面的内容，有一定的知识基础与环境搭建经验，但由于各方面原因总是没有系统性的去学习计算机视觉的相关知识，也缺乏足够的实战代码与项目经验。通过这门课程的学习，很大程度上锻炼了我Python的代码能力，也在Coding的过程中不断熟悉OpenCV、Pytorch等库的使用，更在实践的过程中不断加深对于各种算法模型（AlexNet、ResNet、YOLO等）的理解。

本次项目让我完整地经历了从数据集获取、论文调研及算法代码实现，再到代码调试与模型训练测试，最终将模型应用到实际系统中的全过程，在项目实现的过程中收获了很多课程教学与实验中涉及不到的东西，包括数据集的收集、模型的选择以及作为一个完整项目的代码实现等等多个方面，这也是我第一次使用GPU资源去进行。虽然由于时间等条件的限制，在模型选择上并没有进行深入的调研与充分的对比试验，只是基于自己已知的一些知识对于架构较为简单的自编码器模型与卷积神经网络进行了复现与设计，最终模型的分类精度还有一定的提升空间，但是这也为我后续的自主学习打下了一个良好的基础，希望未来我能在计算机视觉方面有更加深入的学习与探索，也感谢老师的耐心指导与悉心教学。

参考文献

[1] Nosa-Omoruyi M, Oghenekaro L U. AutoEncoder Convolutional Neural Network for Pneumonia Detection[J]. arXiv preprint arXiv:2409.02142, 2024.

[2] Ratiphaphongthon W, Panup W, Wangkeeree R. An improved technique for pneumonia infected patients image recognition based on combination algorithm of smooth generalized pinball SVM and variational autoencoders[J]. IEEE Access, 2022, 10: 107431-107445.

[3] Gayathri J L, Abraham B, Sujarani M S, et al. A computer-aided diagnosis system for the classification of COVID-19 and non-COVID-19 pneumonia on chest X-ray images by integrating CNN with sparse autoencoder and feed forward neural network[J]. Computers in biology and medicine, 2022, 141: 105134.

[4] García-Ordás M T, Benítez-Andrades J A, García-Rodríguez I, et al. Detecting respiratory pathologies using convolutional neural networks and variational autoencoders for unbalancing data[J]. Sensors, 2020,20(4): 1214.

[5] Xia Y. Enhanced Pneumonia Detection in Chest X-Rays Based on Integrated Denoising Autoencoders and Convolutional Neural Networks[J].

[6] El-Shafai W, El-Nabi S A, El-Rabaie E S M, et al. Efficient Deep-Learning-Based Autoencoder Denoising Approach for Medical Image Diagnosis[J]. Computers, Materials & Continua, 2022, 70(3).

[7] Rana N, Marwaha H. Auto encoder-guided Feature Extraction for Pneumonia Identification from Chest X-ray Images[C]//E3S Web of Conferences. EDP Sciences, 2024, 556: 01011.

[8] Ankayarkanni B, Sangeetha P. An Autoencoder-BiLSTM framework for classifying multiple types of lung diseases from CXR images[J]. Multimedia Tools and Applications, 2024: 1-30.

[9] 孙敬,丁嘉伟,冯光辉.一种基于自编码器降维的神经卷积网络入侵检测模型[J/OL].电信科学,1-7[2025-01-05].

[10] 张淙越,杨晓玲.基于卷积神经网络的新冠肺炎CT图像识别系统[J].电脑与信息技术,2022,30(03):12-14+40.

摘要

本项目围绕机器学习分类算法展开， 以支持向量机（support vector machine，SVM）为主要研究对象，探究其分类性能、模型改进与优化算法。SVM和Logistic回归模型都可以用于解决二分类问题，但模型设计的思路不同，因此希望能够比较两者在分类性能上的差异。项目过程中代码完全基于R语言实现，主要以二维样本数据为研究对象，生成模拟数据并基于经典硬间隔SVM模型和Logistic回归模型分别进行建模与训练，在测试集上对模型进行验证，最终比较两者的分类效果差异。实验结果表明，当样本数据本身区分度不明显时，两种分类模型效果均较差，但Logistic模型明显优于经典硬间隔SVM；当样本数据本身具有明显的差异性时，两种分类模型效果均较好，SVM略优于Logistic。此外，还对改进后的SVM模型（核函数由线性函数更换为高斯核函数）进行性能测试，发现其在区分度不明显的数据集上显著优于经典硬间隔SVM，说明其显著提升了其在非线性可分数据上的分类效果；但在区分度较明显的数据集上分类效果反而略逊于经典SVM模型。最后，对两篇有关SVM改进模型的文献进行了阅读与调研，总结了软间隔SVM模型在正则项和损失项拓展方面的研究进展，并介绍了柔性套索惩罚和快速截断Huber损失等改进方法。

关键词: 机器学习分类算法、二分类、支持向量机（SVM）、Logistic回归、硬间隔、软间隔、高斯核函数、改进的SVM模型、柔性套索惩罚、快速截断Huber损失、R语言

项目概述

问题背景

人工智能的概念是在1956年首次被提出，其目标旨在希望通过计算机模拟人的思维能力或智能行为，从而让计算机能够像人类一样进行思考。目前，人工智能已经在机器翻译、智能控制、图像识别、语音识别、游戏博弈等领域得到广泛的应用。

机器学习作为人工智能的一个发展方向，起源于20世纪50年代的感知机数学模型，其目标是使得机器能够像人类一样具有学习能力。机器学习的基本过程主要是基于样本数据（客体）去训练/学习某个模型或决策函数（主体）。一般而言，正则化框架下的机器学习过程主要由学习机、损失项和正则项（惩罚项）三个部分构成，最终通过学习得到模型。

支持向量机(support vector machine，SVM)最早由Cortes和Vapnik二人于1995年为解决二分类问题而提出[^1]。作为经典的机器学习模型之一，SVM有坚实的统计理论基础，算法实现容易，且决策函数具有很强的几何含义。由于其在模式识别等数据分析问题中的优越表现，SVM如今已成为最经典的判别分析方法之一。与SVM相类似，广义线性回归统计模型中的Logistic回归模型同样也可用于解决二分类问题。本质上来说，两种方法都注重研究一组协变量X_1, …, X_p是如何影响二元的响应变量Y的，在用途上具有极大的相似性，因而希望研究并比较两者分类效果的差异性。

除此之外，SVM作为一种经典且基础的机器学习算法，在漫长的发展历程中也经历了多次迭代，有多种多样的改进版本。最基本的版本为硬间隔SVM，但由于实际的样本数据很可能不满足线性可分的理想情况，又发展出了采用不同求解算法的软间隔SVM模型以及基于核函数升维思想实现的非线性SVM，基于软间隔SVM模型又集中在模型损失项与正则项两个方面进行了理论上的拓展。这样的发展是永无止境的，在此希望对过去的部分研究改进成果进行理论总结与代码实现，以更好地了解SVM模型的发展现状。

项目任务

在本次项目中，需要随机生成模拟数据，并在该样本数据基础上分别利用经典SVM模型与Logistic模型进行统计建模，同时对比两者的分类效果；此外还需要总结并实现部分改进版本的SVM算法，分析其预测效果。具体而言可细分为如下任务：

• 任务1:随机生成200条模拟数据并将其分为训练数据集与测试数据集，利用训练数据集分别基于经典硬间隔SVM模型与Logistic广义线性回归模型建立统计模型，实现样本数据的分类且在测试数据集上进行验证，比较两者的分类效果差异。

• 任务2:代码实现某一种改进版本的SVM模型，简单测试其性能并将其分类结果与经典版本进行对比。

• 任务3:查阅SVM模型改进相关的文献，基于正则化框架对于文献中涉及的模型（学习机、损失项、正则项）、创新点与求解算法进行重述与总结。

项目过程

本项目代码部分完全基于R语言实现，主要涉及样本模拟数据的生成，以及SVM（经典与改进版本）与Logistic回归模型的建立、训练与测试。

模拟数据生成

本项目中涉及到的样本数据完全由模拟方法生成。具体而言，不论是SVM还是Logistic回归模型，其目的都是为了研究一系列协变量对于一个二元的响应变量的影响。为方便起见，选择采用协变量的维度为二维，即二元响应变量Y只由两个变量X_1, X_2决定。在生成数据时，为了较好地区分出两类数据，分别在正态总体下以均值为0和均值为1生成两组模拟数据（同一条数据中的两个变量X_1, X_2来自同一均值的总体），并分别打上分类标签（即对应Y的取值为）0或1：

1
2
3
4
5
6
7
8
9
10
11
12

set.seed(123) #设置随机种子，固定每次运行程序生成的随机数，使结果可重复
n <- 200  # 每个类别的数据点数

# 生成类别0的数据
x1 <- matrix(rnorm(n * 2, mean = 0), ncol = 2)
y1 <- rep(0, n)
# 生成类别1的数据
x2 <- matrix(rnorm(n * 2, mean = 1), ncol = 2)
y2 <- rep(1, n)
# 合并数据
x <- rbind(x1, x2)
y <- c(y1, y2)

绘制样本点对应的散点图，初步观察其分类情况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 加载 ggplot2 包
library(ggplot2)

# 创建数据框
data <- data.frame(x1 = x[, 1], x2 = x[, 2], y = factor(y))

# 设置点的大小和透明度
p <- ggplot(data, aes(x = x1, y = x2, color = y)) +
geom_point(size = 3, alpha = 0.7) +  # 调整点的大小和透明度
scale_color_manual(values = c("blue", "red")) +
labs(x = "x1", y = "x2", color = "Class") +
theme_minimal()

# 调整背景和边界线
p + theme(panel.background = element_rect(fill = "white", color = "black"),
panel.border = element_rect(color = "black", fill = NA),
axis.line = element_line(color = "black"))

ggsave("2.png", plot = p, width = 6, height = 6, units = "in", dpi = 300)

观察上左图可知，由于基于正态总体生成模拟数据时仅制定了均值而未指定方差（默认为1），导致令均值为0和1的情况下两类数据没有办法明显的区分开来，这样的分类效果显然是不好的。经过调试，当设置两类数据均值分别为0和5时，数据点呈现良好的区分性（如上右图所示）。

为便于后续的模型训练，还需要将样本模拟数据分成训练集与测试集两部分，根据经验，较为合适的数据集数量比例为7：3，即样本数据中的70%为训练集，另外30%为测试集用于验证。

1
2
3
4
5
6
7
8
9
10

# 将数据分为训练集和测试集
train_index <- sample(1:(2 * n), 0.7 * 2 * n)
x_train <- x[train_index, ]
y_train <- y[train_index]
x_test <- x[-train_index, ]
y_test <- y[-train_index]

# 合并 
train_data <- cbind(x_train, y_train)
test_data <- cbind(x_test, y_test)

在此对部分训练集数据进行罗列：

1
2

#观察数据集
head(train_data,10)

基于经典硬间隔SVM模型的建模

硬间隔支持向量机是一种基于线性可分数据集的分类模型。线性可分，意味着可用一条直线将两类数据分开。显然这样的直线有无穷多条，但对应直线的上下移动又因分类要求的限制而存在极限位置。因此，硬间隔支持向量机所要解决的关键问题就是，如何从无穷多条直线（对应无穷多个分类器）中选择最优？

实际上，具有”最大间隔”的分类器就是SVM要寻找的最优解，而最优解对应的两侧虚线（上下极限状态）所穿过的样本点，就是SVM中的支持样本点，称为"支持向量"。SVM中寻找最优分类器的问题，本质上是一个优化问题。对于一般的优化问题，往往有3个基本要素需要重点关注：

• 目标函数:希望优化的目标指标；

• 优化对象:期望通过改变哪些因素（协变量）使目标函数达到最优；

• 约束条件:优化对象一般需要满足一些特定的约束条件。

假定
$$
{ {({x_i}^T,y_i)} }_{i=1}^n
$$
表示一个二分类数据集，其中第i个样本x_i ∈ R^p，样本对应的标签y_i ∈ {-1,+1}, i=1, …, n。对于优化对象x_i而言，可以根据解析几何的基本知识构造其分类器（超平面）的一般表达式：

$$
w_1x_1+\cdots+w_px_p+b=w^Tx+b=0
$$
其中
$$
w={(w_1,\cdots,w_p)}^T
$$
为该超平面的法向量，b为超平面的截距。

显然，SVM中的优化对象就是上述分类器，或者说超平面中的参数w, b。在本项目的模拟数据中，令样本协变量维度p=2，此时分类器为R^3上的平面。

在线性SVM算法中，目标函数显然就是”分类间隔”，即目标是最大化“分类间隔”W=2d (如下图所示)。其中d表示“支持向量”到最优分类器的距离，最大化W等价于最大化d。

最后是约束条件的确定。首先要考虑的就是，如何判断超平面是否将样本点正确分类？此外，目标函数本质上是求距离d的最大值，要确定约束条件，还必须要找到哪些是”支持向量”。总而言之，对于目标函数d的取值范围受到的限制和约束条件的确定，关键问题是如何将其数学化。

以上述平面上的分类问题为例：对任意一点x_i，其到最优分类直线的距离为
$$
d_i=\frac{|w^Tx_i+b|}{||w||}
$$
一方面，如果此时最优分类直线确实实现了分类目标，则所有样本点(y_i =1 or -1)必定都要满足约束(d 为最优距离)：
$$
d_i=\frac{|w^Tx_i+b|}{||w||}\geq d \Leftrightarrow
\begin{cases}
\frac{w^Tx_i+b}{||w||}\geq d,\ y_i=1\ \
\frac{w^Tx_i+b}{||w||}\le-d,\ y_i=-1
\end{cases}
\Leftrightarrow \ y_i\bullet\frac{w^Tx_i+b}{||w||}\geq d\
\Leftrightarrow \frac{1}{||w||d}\bullet y_i(w^Tx_i+b)\geq1
$$
注意到:
$$
w^Tx+b=0与\frac{1}{||w||d}\bullet(w^Tx+b)=0
$$
本质上代表同一个超平面，因此上述约束条件可以等价改写为：
$$
y_i(w^Tx_i+b)\geq1
$$
另一方面，注意到”支持向量”都是位于最优分类超平面上，即若点(x_i, y_i)为”支持向量”，则必有：
$$
w^Tx_i+b=1
$$
于是最大化目标函数(“支持向量”到最优分类超平面的间隔)，等价于最大化：
$$
\frac{1}{||w||}
$$
也等价于最小化：
$$
\frac{1}{2}{||w||}^2
$$
综上所述，硬间隔SVM的基本数学模型可以描述为如下不等式约束的二次型函数的约束优化问题：
$$
\begin{cases}
\mathop{min}\limits_{w,b}{ {\frac{1}{2}||w||}^{2} }\
st:\ y_i(w^Tx_i+b)\geq1,\ i=1,\cdots,n \
\end{cases}
$$
该优化问题由于受不等式约束，因此求解过程中还需要考察拉格朗日对偶问题和KKT条件。基于不等式约束的凸优化问题，可以基于拉格朗日对偶问题和KKT条件，然后利用SMO算法求解,得到最优w*, b*，从而可构造最优分类超平面：
$$
{(w^\ast)}^Tx+b^\ast=0
$$
对待分类的样本点x，根据以下决策函数来进行分类判别
$$
f(x)=sgn({(w^\ast)}^Tx+b^\ast)
$$
即当
$$
{(w^\ast)}^Tx+b^\ast>0
$$
时返回0，否则返回1。

基于以上理论， 可实现经典硬间隔SVM模型建构。在R语言中，e1071程序包内的svm()函数是对于经典硬间隔SVM模型的封装实现，其基本用法如下：

1
2

# 训练 SVM 模型
model <- svm(formula,data,labels,scale=TRUE/FALSE,kernel,gamma=g,degree=d,cost=C,epsilon=0.1,na.action=na.omit/na.fail)

其中：

• formula:拟合公式，以R公式的形式指定输出变量和输入变量，其格式一般为：输出变量名 输入变量名；

• data:训练数据集（各协变量），通常是一个数据框或矩阵；

• labels:标签数据（二元响应变量），通常是一个因子向量，用于指定那些将被用来训练模型的采样数据;

• scale:逻辑向量，指定特征数据是否需要标准化(默认标准化为均值0，方差1)，默认为True;

• kernel:核函数类型， 常用的有"linear"、"polynomial"、"radial" (RBF) 和 "sigmoid";

• gamma:用于指定多项式核以及径向基核中的参数，默认gamma是线性核中的常数项，等于1/p(p为特征空间中的维度);

• degree:用于指定多项式核中的阶数d;

• cost:惩罚参数，用于控制误分类的惩罚程度;

• epsilon:用于指定支持向量回归中的带，默认值为0.1;

• na.action:用于指定当样本数据中存在无效的空数据时系统应该进行的处理，默认值na.omit表明程序会忽略那些数据缺失的样本；另外一个可选的赋值是na.fail，它指示系统在遇到空数据时给出一条错误信息。

硬间隔支持向量机（Hard-Margin SVM）是支持向量机的一种特殊情况，适用于数据完全线性可分的情况。它通过最大化间隔来找到一个分离超平面，使得所有数据点都在间隔之外且没有误分类点。为实现经典的硬间隔SVM模型，可以将svm()函数的参数如下设置：

1
2
3
4

# 训练硬间隔SVM模型
library(e1071) # 需要先导入e1071库
cost_value <- 1e5 # 设置 cost 为一个非常大的值，从而确保没有误分类
svm_model <- svm(x_train,y_train, type = "C-classification", kernel = "linear", cost = cost_value, scale = FALSE)

可以通过summary()方法查看训练出的模型的信息：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

summary(svm_model)
	
Call:
svm.default(x = x_train, y = y_train, scale = FALSE, type = "C-classification",
kernel = "linear", cost = cost_value)

Parameters:
SVM-Type:  C-classification   #模型类别
SVM-Kernel:  linear   #模型使用的核函数
cost:  1e+05   #模型确定的约束违反成本
Number of Support Vectors:  2	( 1 1 )  
#模型找到的支持向量数量，两类各有一个
Number of Classes:  2
Levels:	0 1   #模型中分类的目标类别

至此已经基于训练集数据完成了经典硬间隔SVM模型的建立与训练过程。

基于Logistic回归模型的建模

与SVM模型类似，Logistic回归模型也旨在研究协变量X_1, …, X_p是如何影响响应变量y的。但不同的是，Logistic作为广义线性回归模型的一种，本质上还是基于”回归”的基本思想，在多元线性回归的基础上进行调整从而能够处理离散的二元数据。

假定对二元响应变量y有n次观测：
$$
\ y_i \sim B(1,\mu_i),\ i=1,\cdots,n
$$
显然其均值方差分别为：
$$
{E(y}i)=\mu_i;\ Var(y_i)=\mu_i(1-\mu_i)
$$
同时，对协变量X_1, …, X_p也有n次观测，且记其线性组合分别为：
$$
\eta_i=\beta_0+x{i1}\beta_1+\cdots+x_{ip}\beta_p=x_i^T\beta,\ i=1,\cdots,n
$$
其中：
$$
x_i={(1,x_{i1},\cdots,x_{ip})}^T, \beta={(\beta_0,\beta_1,\cdots,\beta_p)}^T
$$
在多元线性回归的过程中，由于响应变量y连续，因此可以直接令其均值E(y)等于协变量与未知参数的线性组合η；但对于二元（取值仅存在0或1两种情况）的响应变量而言，这样简单粗暴的处理方式显然是不合适的，需要在原来的方法上做推广，即”广义”的线性回归模型：既然无法直接令两者相等，不妨寻找一个链接函数，将多元线性回归中值域为R的协变量线性组合
$$
\eta_i=x_i^T\beta
$$
映射到μ_i ∈ (0*,* 1)区间上，从而便于分类过程的实现。

具体而言，在建立广义线性回归模型的过程中，需要在多元线性回归的基础上选取合适的链接函数g(•)把y_i的期望µ_i = E(y)和协变量的线性组合η _i = x_i^T * β联系起来，使得g(µ _i) = η _i。这样的链接函数应该具有良好的性质（如光滑等），才便于后续计算。

针对二元响应变量的分类过程，常用的连接函数为Logistic链接函数：
$$
g(x)=ln{\frac{x}{1-x}},\ x\in(0,1)
$$
基于Logistic链接函数构造的广义线性回归模型即为Logistic回归模型，其基本内容如下：
$$
\begin{cases}
y_i \sim B(1,\mu_i), i=1,\cdots,n \
g(\mu_i)=\mu_i=x_i^T\beta
\end{cases}
$$
事实上，基于给定的样本数据（训练集数据），训练模型的过程即为对未知参数向量β进行极大似然估计的过程，但与线性模型不同的是，该模型中极大似然估计并没有显式解，因此需要基于特定的算法进行数值求解，一般采用Newton-Raphson迭代算法，这里不详细展开求解过程。

在R语言中，Logistic模型的训练由基本包中自带的glm()函数实现，其基本用法如下：

1
2

# 训练广义线性模型
model <- glm(formula, data = mydata, family = family(link = "link_function"))

其中：

• formula:表示响应变量与解释变量的关系公式，如y ∼ x1 + x2；

• data:所用的数据集（需要为数据框格式来识别特征和标签）；

• family:表示所拟合的GLM模型类型，包括（但不限于）高斯、二项分布、泊松分布等;

• link:表示链接函数，常见的有"identity"、”logit”、"log"等。

为实现广义回归模型中的Logistic回归模型，可按照如下方式进行调用：

1
2
3
4
5

# 将训练数据转换为数据框
train_data <- data.frame(x = x_train, y = as.factor(y_train))

# 训练Logistic回归模型
logistic_model <- glm(y ~ ., data = train_data, family = binomial)

同样采用summary()方法查看训练模型的信息：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

summary(logistic_model)

Call:   # 调用信息, 说明模型使用了二元逻辑回归和所有特征。
glm(formula = y ~ ., family = binomial, data = train_data)

Coefficients:   # 估计值、标准误差、z值和p值的表格。
(Intercept)  -169.33   32205.14  -0.005    0.996
# 截距项的估计值、标准误差、z值和p值。
x.1            15.32    5873.78   0.003    0.998
# 第一个特征x.1的估计值、标准误差、z值和p值。
x.2            63.10   13139.18   0.005    0.996
# 第二个特征x.2的估计值、标准误差、z值和p值。
(Dispersion parameter for binomial family taken to be 1)
# 二项分布的离散参数被设定为1。
Null deviance: 3.8815e+02  on 279  degrees of freedom
# 零偏差：模型中只有截距时的偏差, 279个自由度。
Residual deviance: 6.1211e-08  on 277  degrees of freedom
# 残差偏差：模型拟合后的偏差, 277个自由度。
AIC: 6	# AIC 值（信息准则）, 用于模型选择。
Number of Fisher Scoring iterations: 25   
# Fisher评分算法的迭代次数。

至此已经基于训练集数据完成了Logistic回归模型的建立与训练过程。

二者分类效果的比较

前文在生成模拟数据的过程中提到，若生成时设置的正态总体均值差异不同，其聚集效果也会不同，在默认方差为1的情况下，设置均值为0和1的数据点区分不明显，而设置均值为0和5的数据点区分明显。在模型效果测试中，为保证模型聚合等多方面因素，分别选用均值为0和1（数据点区分不明显），以及均值为0和2.8的数据（数据点区分明显）进行模型训练与性能测试。

首先是选用均值为0和1的数据，即标签为0的数据应聚集在点(0, 0)附近，标签为1的数据应聚集在点(1, 1)附近。将训练好的模型应用于测试集上并计算其分类准确率，同时绘制其分类结果与分类器效果图像：

1
2
3
4
5
6
7
8
9
10

# 使用SVM模型进行预测
svm_predictions <- predict(svm_model, x_test)
# 计算SVM模型的分类准确率
svm_accuracy <- sum(svm_predictions == y_test) / length(y_test)

# 使用Logistic回归模型进行预测
logistic_probabilities <- predict(logistic_model, newdata = data.frame(x = x_test), type = "response")
logistic_predictions <- ifelse(logistic_probabilities > 0.5, 1, 0)
# 计算Logistic回归模型的分类准确率
logistic_accuracy <- sum(logistic_predictions == y_test) / length(y_test)

运行程序，得到该情况下SVM模型的分类准确率为0.525，Logistic回归模型的分类准确率为0.767。结合观察图像可知，此时对于区分不明显的数据，两个模型的分类效果都较差（90%以下），但Logistic回归模型在数据区分不明显的情况下分类性能要明显优于经典硬间隔SVM模型。

然后选用均值为0和2.8的数据，即标签为0的数据应聚集在点(0, 0)附近，标签为1的数据应聚集在点(2*.8, 2.*8)附近。将训练好的模型应用于测试集上并计算其分类准确率，同时绘制其分类结果与分类器效果图像：

运行程序，得到该情况下SVM模型的分类准确率为0.967，Logistic回归模型的分类准确率为0.950。结合观察图像可知，此时对于区分较明显的数据，两个模型的分类效果都较好（90%以上），但经典硬间隔SVM模型在数据区分较明显的情况下分类性能会略优于Logistic回归模型，但总体而言差异并不是很大。

改进后SVM模型的性能测试

上述内容中用到的经典硬间隔SVM模型实际上对于数据有着较高的要求，其实现依赖于样本数据为线性可分这一假设条件，但现实中的实际数据往往很难满足这一点，这也是其缺陷所在。针对不是线性可分的数据，Cortes和Vapnik采用了一种非常巧妙的方式进行改进，即借助函数映射，将低维数据映射到高维空间中，使得在低维空间原来不能线性可分的数据，在高维空间变得线性可分，且可以证明这样的映射始终存在。

具体而言，构造升维函数：
$$
K(x,z)=\varphi(x)\bullet\varphi(z)
$$
并构造相应的非线性SVM：
$$
\begin{cases}
\mathop{min}\limits_{w,\ b,\ \delta_i} { {\frac{1}{2}||w||}^2} \
st:\ y_i(w^TK(x_i,z)+b)\geq1,\ \ i=1,\cdots,n
\end{cases}
$$
相应的最优分类超平面为：
$$
{(w^\ast)}^TK(x_i,z)+b^\ast=0
$$
这里选择高斯函数(径向基函数RBF)作为核函数，将每一个样本点映射到一个无穷维的特征空间从而实现降维，构造改进的SVM模型：
$$
K(x, x’) = \exp\left(-\gamma | x - x’ |^2\right)
$$
高斯核函数实现的功能是：先将原始的数据点(x, y)映射为新的样本(x′, y′)，再将新的特征向量点乘(x′, y′)，返回其点乘结果。其主要目的是找到更有利分类任务的新的空间，本质是在衡量样本和样本之间的”相似度”，在一个刻画”相似度”的空间中，让同类样本更好的聚在一起，进而线性可分。

在R语言中，要实现高斯核函数，仅需将调用的svm()函数中的参数进行改变：

1
2

# 训练改进后的非线性SVM模型
svm_model_modify <- svm(x_train,y_train, type = "C-classification", kernel = "radial", gamma = 2, cost = 1, scale = FALSE)

其中核函数类型的参数kernel由原先的线性函数”linear”更换为高斯核函数”radial”，并对核函数中的参数gamma以及控制误分类的惩罚参数cost进行了相应调整。

在样本数据区分不明显（即总体均值设置为0和1）的情况下，运行程序，得到改进后的非线性SVM模型的分类准确率为0.767，与Logistic回归模型在该样本下的分类准确率一致，较原先经典硬间隔SVM的预测准确率0.525有显著提升。改进后模型的分类效果如下图所示。

在样本数据区分较明显（即总体均值设置为0和2.8）的情况下，运行程序，得到改进后的非线性SVM模型的分类准确率为0.958，虽然仍优于Logistic回归模型在该样本下的分类效果，但较原先经典硬间隔SVM的预测准确率0.967有略微下降。尽管如此，改进后的模型分类准确率仍然在0.95以上，具有良好的分类效果。改进后模型的分类效果如下图所示。

文献调研

硬间距SVM要求构建的分类超平面完全正确的分类所有训练数据，但由于实际样本被假设成线性可分的条件太强，为避免过拟合，更多时候需要考虑软间距（soft-margin）SVM模型。

所谓软间距，就是允许一些点不满足线性可分的约束条件，即：
$$
y_i\left(w^Tx_i+b\right)<1
$$
当然，为保证拟合模型仍然为一种SVM方法的”本性”，我们希望这样的点不能太多，因此要对违反约束的样本点(x_i, y_i)施加一定的非负惩罚（松弛变量）δ_i：
$$
\delta_i=max{0, 1-y_i\left(w^Tx_i+b\right)}=
\begin{cases}
0, y_i\left(w^Tx_i+b\right)\geq1\ \
1-y_i\left(w^Tx_i+b\right),\ y_i\left(w^Tx_i+b\right)<1
\end{cases}
$$
这样就可以得到软间隔SVM的基本数学模型：
$$
\begin{cases}
\mathop{min}\limits_{w,\ b,\ \delta_i} { {\frac{1}{2}||w||}^2+c\sum_{i=1}^{n}\delta_i} \
st:\ y_i(w^Tx_i+b)+\delta_i\geq1,\ \delta_i\geq0,\ i=1,\cdots,n
\end{cases}
$$
值得注意的是，每一个样本都有一个对应的松弛变量，表征该样本不满足约束的程度；c>0为惩罚参数，其值越大，对分类的惩罚越大。跟硬间隔SVM一样，先用拉格朗日乘子法得到拉格朗日函数，再求其对偶问题。

在正则化的框架下，软间隔SVM的基本数学模型结构还可改写为：
$$
\mathop{min}\limits_{w,\ b,\ \delta_i} { {\frac{1}{2}||w||}^2+c\sum_{i=1}^{n}\delta_i}
$$
其中学习机、损失项、正则化项分别定义为：

• 学习机：
  $$
  f\left(w\right)=w^Tx+b
  $$

• 损失项：
  $$
  c\sum_{i=1}^{n}\delta_i
  $$

• 正则项：
  $$
  \frac{1}{2}w^Tw={\frac{1}{2}||w||}^2
  $$

基于软间隔SVM模型，理论上的拓展主要集中在模型损失项与正则项两个方面，针对这两个方面，接下来将分别选取一篇文献，对其改进模型、求解算法与创新点进行简单的书面总结。

正则项拓展：柔性套索惩罚[^2]

模型重述

柔性套索（Pliable lasso）是一种新的互动模型，由Robert Tibshirani和Jerome Friedman于2018年提出。该模型是原始套索问题的扩展，允许套索回归模型接受修改变量、预测因子和结果。原始的套索（Lasso）问题本质上是将1-范数作为正则项，而柔性套索是在此基础上的改进。1-范数支持向量机的缺点之一是，在一些输入高度相关的情况下，并且所有输入都与输出相关，1-范数惩罚最终会挑选出少数输入，并将其余的减少到零，这意味着”群体选择”将是对1范数支持向量机的挑战。

柔性套索惩罚允许估计协变量X的主要影响以及协变量与一组修饰符Z之间的相互作用影响，以处理相互作用效应。为了处理变量选择并帮助选择相关变量组，引入修正变量Z，并将柔性套索作为正则项（惩罚项），得到具有柔性套索惩罚的SVM目标函数：
$$
\min_{\beta, h} \left( \frac{1}{n} \sum_{i=1}^n (1 - y_i (\beta_0 + x_i^T \beta))+^2 + \lambda_1 \left( \sum{j=1}^p |\beta_j|1 + \sum{j=1}^p |h_j|_1 \right) + \frac{\lambda_2}{2} \left( |\beta|2^2 + \sum{j=1}^p |h_j|_2^2 \right) \right)
$$
其中，学习机、损失项和正则化项（惩罚项）定义如下：

• 学习机：
  $$
  y = \beta_0 + Z h_0 + \sum_{j=1}^p X_j (\beta_j + Z h_j) + \epsilon_i
  $$

• 损失项：损失平方和（hinge函数）
  $$
  \frac{1}{n} \sum_{i=1}^n (1 - y_i (\beta_0 + x_i^T \beta))^2
  $$

• 正则项：柔性套索惩罚
  $$
  \lambda_1 \left( \sum_{j=1}^p |\beta_j|1 + \sum{j=1}^p |h_j|_1 \right) + \frac{\lambda_2}{2} \left( |\beta|2^2 + \sum{j=1}^p |h_j|_2^2 \right)
  $$

求解算法与创新点

在目标函数优化的求解过程中， 主要使用块方向坐标下降过程（the block-wise coordinate descent procedure）优化目标函数：

本篇文章在过去已有模型的基础上再次进行了改进，创造性地把柔性套索（优化后的1-范数）作为惩罚项（正则项）引入软间隔SVM模型中，创新点有如下几条：

• 可调套索惩罚的应用：将可调套索惩罚应用于支持向量机，能够有效估计协变量与修饰变量之间的交互作用。

• 交互项排除机制：通过可调套索，能够在相应主效应为零时自动排除交互项，提高模型的解释性和简洁性。

• 平方铰链损失结合块坐标下降算法:使用该组合优化目标函数，在模拟和实际数据（结肠癌和前列腺癌数据集）上验证了方法的有效性。

损失项拓展：快速截断Huber损失[^3]

模型重述

支持向量机作为一种有用的分类工具，在许多领域得到了广泛的应用。然而，在非常大的样本数据集上，它可能会导致计算上的不可行性。为了解决这一问题，该文章提出了一种新颖的带有截断Huber损失的稀疏鲁棒支持向量机模型，即L_th-SVM，其基本数学模型如下：
$$
\min_{w \in \mathbb{R}^n, b \in \mathbb{R}} \frac{1}{2} |w|^2 + \gamma \sum_{i=1}^m \ell_{th}(1 - y_i(\langle w, x_i \rangle + b))
$$
也可写作：
$$
\min_{w \in \mathbb{R}^n, b \in \mathbb{R}} \frac{1}{2} |w|^2 + \gamma \sum_{i=1}^m \ell_{th}(h)
$$
其中，学习机、损失项和正则化项（惩罚项）定义如下：

• 学习机：
  $$
  h:= \mathbf{1} - \mathcal{G}\mathbf{w} - b\mathbf{y} \in \mathbb{R}^{m},其中\begin{aligned}
  \mathcal{G} &:= \left[ \begin{array}{cccc}
  y_{1}x_{1} & y_{2}x_{2} & \cdots & y_{m}x_{m}
  \end{array} \right]^{\top} \in \mathbb{R}^{m \times n}
  \end{aligned}
  $$

• 损失项：快速截断Huber损失（Truncated Huber Loss）：
  $$
  \ell_{\text{th}}(t) = \begin{cases}
  1, & \text{if } t > 1 + \frac{\delta}{2}, \
  t - \frac{\delta}{2}, & \text{if } t \in \left[\delta, 1 + \frac{\delta}{2}\right], \
  \frac{t^2}{2\delta}, & \text{if } t \in [0, \delta), \
  0, & \text{if } t < 0.
  \end{cases}
  $$

• 正则项：L2正则化
  $$
  \frac{1}{2}w^Tw={\frac{1}{2}||w||}^2
  $$

求解算法与创新点

针对L_th-SVM问题，文章提出了一种新颖高效的乘子与工作集交替方向的方法L_th-ADMM)，证明了L_th-ADMM产生的序列是L_th-SVM的局部最小值，并且在工作集很小的情况下具有较低的计算复杂度。大量的数值实验表明，L_th-ADMM能够提供更高的预测精度，提供更少的支持向量，并且运行速度快，特别是在大规模数据集设置中。其求解算法大致如下：

本文的创新点主要包括以下几个方面：

• 截断Huber损失函数的提出：提出了一种新的截断Huber损失函数，该函数能够在保持稀疏性的同时，增加对异常值的鲁棒性。与现有的hinge损失、huberized pinball损失和Huber损失相比，截断Huber损失函数在稀疏性和鲁棒性方面表现出更优的性能。

• 稀疏鲁棒SVM模型的构建：基于截断Huber损失函数，构建了新的稀疏鲁棒支持向量机模型（Lth-SVM）。该模型不仅继承了SVM分类能力强、理论框架完善等优点，还通过引入截断Huber损失函数提高了模型的稀疏性和鲁棒性，使其在处理大规模分类问题时更加有效。

• 一阶最优性条件的建立：为L_th-SVM模型建立了基于新引入的P-稳定点的一阶必要和充分条件，定义了L_th支持向量和工作集。这些条件为算法设计提供了理论基础，同时也证明了所有L_th-SVM支持向量仅占整个训练集的一小部分，这为后续开发高效算法提供了可能。

• L_th-ADMM求解算法的设计：提出了一种具有工作集的新型交替方向乘子法（L_th-ADMM）来求解L_th-SVM。该算法通过引入工作集策略，显著降低了每次迭代中的计算复杂度，使得算法在处理大规模数据集时能够快速收敛。同时，理论证明表明，该算法生成的序列能够收敛到L_th-SVM的一个局部极小值。

参考文献

[^1]: Cortes C, Vapnik V. Support-vector networks[J]. Machine learning, 1995, 20(3): 273-297.
[^2]: Asenso, T. Q., Wang, P., & Zhang, H. (2022). Pliable lasso for the support vec- tor machine. Communications in Statistics - Simulation and Computation, 53(2), 786–798.
[^3]: Huajun Wang, Yuanhai Shao, Fast truncated Huber loss SVM for large scale clas- sification, Knowledge-Based Systems, Volume 260, 2023.