研究背景意义

矩阵的特征值计算虽然有比较可靠的理论方法，但是，理论方法只适合于矩阵规模很小或者只是在理论证明中起作用，而实际问题的数据规模都比较大，不太可能采用常规的理论解法。计算机擅长处理大量的数值计算，所以通过适当的数值计算理论，写成程序，让计算机处理，是一种处理大规模矩阵的方法，而且是一种好的方法。乘幂法（又称幂法）是求矩阵按模最大特征值的常用方法，其结构简单、便于使用，在实际工程中应用广泛：

• 在数值分析和优化问题中，乘幂法可通过求解矩阵按模最大特征值来得到其谱半径，从而帮助分析迭代算法的收敛性；
• 在物理学和工程学中，特征值问题常用于分析系统的稳定性、振动频率和模态分析，乘幂法能够有效求解系统的最大特征值，从而帮助理解系统的动态行为；
• 在图像处理中，特征值分解用于图像压缩、特征提取和模式识别，乘幂法可用于求解图像矩阵的最大特征值，从而实现高效的图像处理算法；
• ……

但该方法也存在一定的局限性，其只适用于求矩阵按模最大的特征值，而在实际问题中往往需要求矩阵全部特征值，如在主成分分析中需要求相关矩阵的全部特征值以确定各主成分的贡献率，在求解线性微分方程组中通过求系数矩阵的全部特征值以确定其基础解系；同时该方法在求特定矩阵（如具有一对互为相反数的按模最大特征值的矩阵等）的按模最大特征值时是不收敛的。因此，我们希望以乘幂法基本思想为出发点，在此基础上提出一些改进算法以对其进行泛化，使其能够解决更为广泛且通用的应用场景下的实际问题。

算法基本思想

设n阶矩阵A具有n个线性无关的特征向量
$$
x_1,x_2,…,x_n
$$
相应的特征值
$$
\lambda_1,\lambda_2,…,\lambda_n
$$
满足：
$$
\left|\lambda_1\right|>\left|\lambda_2\right|\geq\left|\lambda_3\right|\geq…\geq\left|\lambda_n\right|
$$
现任取一非零向量u_0，作迭代
$$
u_k=Au_{k-1}, k=0,1,2,…
$$
得到向量序列{u_k}(k=0,1,2,…)。因各特征向量线性无关，故n维向量u_0必可由他们线性表示，即：
$$
u_0=\alpha_{1}x_{1}+\alpha_{n}x_{2}+…+\alpha_{n}x_{n}
$$
显然有：
$$
\begin{aligned}u_{k}&=A^{k}v_{0}=\alpha_{1}A^{k}x_{1}+\alpha_{2}A^{k}x_{2}+\cdots+\alpha_{n}A^{k}x_{n}=\alpha_{1}\lambda_{1}^{k}x_{1}+\alpha_{2}\lambda_{2}^{k}x_{2}+\cdots+\alpha_{n}\lambda_{n}^{k}x_{n}\&=\lambda_{1}^{k}\left[\alpha_{1}x_{1}+\alpha_{2}\left(\frac{\lambda_{2}}{\lambda_{1}}\right)^{k}x_{2}+\cdots+\alpha_{n}\left(\frac{\lambda_{n}}{\lambda_{1}}\right)^{k}x_{n}\right]\end{aligned}
$$
设
$$
\alpha_{1} \neq 0
$$
由
$$
\left|\frac{\lambda_{i}}{\lambda_{1}}\right|<1,i=2,3,\cdots,n
$$
可得：
$$
\operatorname*{lim}{k\to\infty}\frac{u{k}}{\lambda_{1}^{k}}=\operatorname*{lim}{k\to\infty}\frac{\lambda{1}^{k}\left[\alpha_{1}x_{1}+\sum_{i=2}^{n}\alpha_{i}\left(\frac{\lambda_{i}}{\lambda_{1}}\right)^{k}x_{i}\right]}{\lambda_{1}^{k}}=\operatorname*{lim}{k\to\infty}\left[\alpha{1}x_{1}+\sum_{i=2}^{n}\alpha_{i}\left(\frac{\lambda_{i}}{\lambda_{1}}\right)^{k}x_{i}\right]=\alpha_{1}x_{1}
$$

$$
\operatorname*{lim}{k\to\infty}\frac{\left(u{k+1}\right){m}}{\left(u{k}\right){m}}=\operatorname*{lim}{k\to\infty}\frac{\left{\lambda_{1}^{k+1}\left[\alpha_{1}x_{1}+\sum_{i=2}^{n}\alpha_{i}\left(\frac{\lambda_{i}}{\lambda_{1}}\right)^{k+1}x_{i}\right]\right}{m}}{\left{\lambda{1}^{k}\left[\alpha_{1}x_{1}+\sum_{i=2}^{n}\alpha_{i}\left(\frac{\lambda_{i}}{\lambda_{i}}\right)^{k}x_{i}\right]\right}{m}}=\lambda{1}\frac{\left(x_{1}\right){m}}{\left(x{1}\right){m}}=\lambda{1}
$$

这表明向量序列u_k具有收敛性，其收敛速度由比值
$$
\left|\frac{\lambda_{2}}{\lambda_{1}}\right|
$$
确定，该比值越小说明收敛速度越快，比值越接近于1收敛速度就越慢。

同时，该结论表明，当k取得足够大时（在实际应用时往往认为某次迭代前后误差小于设定的误差限即满足该条件），有：
$$
u_{k}≈\lambda_{1}^{k}\alpha_{1}x_{1}, \lambda_{1}≈\frac{\left(u_{k+1}\right)}{\left(u_{k}\right)}
$$
即u_ k可近似看作特征值λ_ 1对应的特征向量（较原特征向量x_ 1而言仅乘上了有限的常数系数，其结果仍为该特征值对应的特征向量），而对应的按模最大特征值λ_ 1的估计值可由前后两次迭代的特征向量u_ k相除得到。

当矩阵的按模最大特征值是重根时，上述结论仍然成立。设λ_ 1为r重根，即：
$$
\lambda_{1}=\lambda_{2}=\cdots=\lambda_{r}
$$
且满足条件
$$
\mid\lambda_{r}\mid>\mid\lambda_{r+1}\mid\geq\cdots\geq\mid\lambda_{n}\mid
$$
则有：
$$
u_{k}=A^{k}u_{0}=\lambda_{1}^{k}\left[\sum_{i=1}^{r}\alpha_{i}x_{i}+\sum_{j=r+1}^{n}\alpha_{j}\left(\frac{\lambda_{j}}{\lambda_{1}}\right)^{k}x_{j}\right]
$$
易推得（式中(u_ k)_ m表示向量u_ k的第m个分量）：
$$
\lim_{k\to\infty}\frac{u_{k}}{\lambda_{i}^{k}}=\sum_{i=1}^{^{r}}\alpha_{i}x_{i},\lim_{k\to\infty}\frac{\left(u_{k+1}\right){m}}{\left(u{k}\right){m}}=\lambda{1}
$$
与一般情况略有不同的是，此时
$$
u_{k}≈\lambda_{i}^{k}\sum_{i=1}^{^{r}}\alpha_{i}x_{i}
$$
但事实上我们并没有办法在求解之前事先预知一个矩阵是否具有r重按模最大特征值，因此在实际操作的过程中采用与一般情形相同的处理方式（即认为r=1），所得的向量序列u_k仍然收敛，不影响求解结果。

基于以上的算法原理，可以编写如下MATLAB程序，实现一般情况下矩阵按模最大特征值及其对应特征向量的计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

function calculatePowerMethod(matrixEdit, iterEdit)
    % 获取用户输入的矩阵matrixEdit和最大迭代次数iterEdit
    A = str2num(matrixEdit.Value); % 将字符串转换为矩阵
    n = length(A);
    V = rand(n,1);  % 以随机方式初始化迭代向量u0
    max_iter = iterEdit.Value;    % 获取迭代次数

    Eps = 1E-4; % 迭代精度
    k = 0; % 初始迭代次数
    lambda0 = 0;

    % 乘幂法迭代，求得矩阵按模最大特征值lambda及其对应特征向量v
    while k <= max_iter - 1
        v = A * V;
        [vmax, i] = max(abs(v));
        lambda = v(i) / V(i);
        V = v;
        if abs(lambda - lambda0)<Eps
            k = k + 1;
            break;
        end
        lambda0 = lambda;
        k = k + 1;
    end
end

改进的乘幂法

在实际应用层面，上述的算法逻辑只在一小部分的常规矩阵上对于矩阵的按模最大特征值求解有较好效果。事实上，仅依托以上的代码逻辑进行求解往往会出现以下几大问题：

1. 当矩阵A不具有n个线性无关的特征向量时（事先无法判断），乘幂法不适用。
2. 当待求取的按模最大特征值abs(λ_ 1)>1时，迭代向量u_ k的各个分量可能会随着abs(λ_ 1)^k变得很大而使计算机“上溢”；而当待求取的按模最大特征值abs(λ_ 1)<1时，迭代向量u_ k的各个分量可能会随着abs(λ_ 1)^k变得很小使u_k成为零向量。
3. 矩阵的按模最大特征值是一对相反数。
4. 矩阵的按模最大特征值是一对共轭复数。

（上述算法中还给出了α_1≠0的假设，事实上如果不满足这一点也不影响乘幂法的成功使用。因为舍入误差的影响，在迭代某一步会产生u_k在x_1方向上的分量不为零，以后的迭代仍会收敛）

针对问题1，我们暂时无法提出具有针对性的解决方案，但后续的实际测试证明，当迭代次数k足够大时，我们针对问题3所提出的改进方案在该种情况下相比基本算法能够有更好的收敛性（收敛更快）；针对问题2，我们可以通过将向量序列u_k进行规范化处理，限制向量的模在特定小范围内，防止计算机运算的上下溢出；针对问题3，我们在原有的乘幂法算法思想的基础上进行了改进，改进后的算法能够有效对原算法无法求解（不收敛）的按模最大特征值互为相反数的矩阵的按模最大特征值进行有效求解；针对问题4，我们目前还没有找到有效的解决方案。

迭代向量的归一化

设迭代向量u为非零向量，将其归一化得到向量
$$
y=\frac{u}{max(u)}
$$
其中max(u)表示向量u的模最大的分量（即向量的无穷范数）。这样的规范化会保证每一次迭代后得到的新的迭代向量的模最大分量均为1，这有效起到了限制迭代向量分量范围的作用，能够很好地解决上述提到的问题2。值得注意的是，对向量规范化的方式并不只有归一化这一种，实际上可以使用任意一种范数对向量进行规范化处理，如2范数等。可以证明，对于基于不同范数的归一化都有相同的向量序列收敛结论，下面以无穷范数为例给出基本的证明。（显然这样的规范化只是在原有的向量基础上除以了某一个常数，这并不会改变向量序列的收敛性）

取初始向量
$$
u_{0}\neq0
$$
规范化得
$$
y_{0}=\frac{u_{0}}{\max(u_{0})}
$$
构造向量序列：
$$
\begin{aligned}
&u_{1}=Ay_{0}=\frac{Au_{0}}{\max(u_{0})},
&y_{1}=\frac{u_{1}}{\max(u_{1})}=\frac{Au_{0}}{\max(Au_{0})}\
&u_{2}=Ay_{1}=\frac{A^{2}u_{0}}{\max(Au_{0})},
&y_{2}=\frac{u_{2}}{\max(u_{2})}=\frac{A^{2}u_{0}}{\max(A^{2}u_{0})}\
&……\
&u_{k}=Ay{{k-1}}=\frac{A^{k}u{0}}{\max(A^{k-1}u_{0})},
&\quad y_{k}=\frac{u_{k}}{\max(u_{k})}=\frac{A^{k}u_{0}}{\max(A^{k}u_{0})}
\end{aligned}
$$
结合乘幂法基本算法中已经证明的结论
$$
A^{k}u_{0}=u_{k}≈\lambda_{1}^{k}\alpha_{1}x_{1}
$$
则有：
$$
\lim_{k\to\infty}y_{k}=\frac{x_{1}}{\max(x_{1})},
\lim_{k\to\infty}\max(u_{k})=\lambda_{1}
$$
这表明此时y_ k可近似看作特征值λ_ 1对应的特征向量（较原特征向量x_ 1而言仅进行了归一化处理，其结果仍为该特征值对应的特征向量），而对应的按模最大特征值λ_ 1的估计值可近似看作未归一化前的迭代向量最大分量值max(u_k)。

基于以上的算法原理，可以编写如下MATLAB程序，实现归一化处理下矩阵按模最大特征值及其对应特征向量的计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

function calculatePowerMethod(matrixEdit, iterEdit)
    % 获取用户输入的矩阵matrixEdit和最大迭代次数iterEdit
    A = str2num(matrixEdit.Value); % 将字符串转换为矩阵
    n = length(A);
    V = rand(n,1);  % 以随机方式初始化迭代向量u0
    max_iter = iterEdit.Value;    % 获取迭代次数

    Eps = 1E-4; % 迭代精度
    k = 0; % 初始迭代次数
    lambda0 = 0;

    % 乘幂法迭代，求得矩阵按模最大特征值lambda及其对应特征向量v
    while k <= max_iter - 1
        v = A * V;
        [vmax, i] = max(abs(v));
        lambda = v(i);
        V = v / lambda;
        if abs(lambda - lambda0)<Eps
            k = k + 1;
            break;
        end
        lambda0 = lambda;
        k = k + 1;
    end
end

归一化乘幂法的进一步改进

针对问题3，从其基本情形出发（其他条件与先前保持一致），即有：
$$
\mid\lambda_1\mid=\mid\lambda_2\mid>\mid\lambda_3\mid\geqslant\cdotp\cdotp\cdotp\geqslant\mid\lambda_n\mid，\lambda_1=-\lambda_2
$$
在矩阵按模最大特征值为一对相反数的情况下，原迭代向量序列中各相邻向量的比值极限发散：
$$
\lim_{k\to\infty}\frac{\boldsymbol{u}_{k+1}}{\boldsymbol{u}k}=\lambda_1\lim{k\to\infty}\frac{a_1\boldsymbol{x}_1+(-1)^{k+1}a_2\boldsymbol{x}2+\boldsymbol{\varepsilon}{k+2}}{a_1\boldsymbol{x}_1+(-1)^ka_2\boldsymbol{x}_2+\boldsymbol{\varepsilon}_k}
$$
说明在该种情况下，采用原有的乘幂法基本算法，得到的迭代向量序列并不收敛，无法得到稳定的矩阵按模最大特征值数值求解结果。

我们在原有算法的基础上进行了一定的改进，构造了新的迭代向量序列，使其对于矩阵按模最大特征值为一对相反数的情况也能保证收敛，从而可以对该情况下的矩阵按模最大特征值进行有效求解。

先从较为简单的非归一化迭代入手，同样取迭代向量序列u_k，其初始非零向量u_0满足：
$$
u_0=\alpha_{1}x_{1}+\alpha_{n}x_{2}+…+\alpha_{n}x_{n}(\alpha_{1}\neq0)
$$
则有：
$$
\boldsymbol{u}{k}=\boldsymbol{A}^{k}\left(\sum{i=1}^{n}a_{i}\boldsymbol{x}{i}\right)=\lambda{1}^{k}\left(a_{1}\boldsymbol{x}{1}+(-1)^{k}a{2}\boldsymbol{x}{2}+\sum{i=3}^{n}\left(\frac{\lambda_{i}}{\lambda_{1}}\right)^{k}a_{i}\boldsymbol{x}{i}\right)=\lambda{1}^{k}(a_{1}\boldsymbol{x}{1}+(-1)^{k}a{2}\boldsymbol{x}{2}+\boldsymbol{\varepsilon}{k}),\lim_{k\to\infty}\varepsilon_{k}=0
$$
于是可得到：
$$
\lim_{k\to\infty}\frac{u_{k+2}}{u_{k}}=\lambda_{1}^{2}\lim_{k\to\infty}\frac{\alpha_{1}x_{1}+(-1)^{k+2}\alpha_{2}x_{2}+\varepsilon_{k+2}}{\alpha_{1}x_{1}+(-1)^{k}\alpha_{2}x_{2}+\varepsilon_{k}}=\lambda_{1}^{2}
$$
且有：
$$
\lim_{k\to\infty}\frac{u_{k+1}+\lambda_1u_k}{\lambda_1^{k+1}}=2\alpha_1x_1
$$
以上结果说明，在矩阵按模最大特征值为一对相反数（正值λ_ 1，负值λ_ 2）的情形下，若采用原有的迭代向量序列，对序列中的向量一隔一取出，构成的新序列是收敛的，且新序列中的相邻两项向量的比值极限为矩阵按模最大特征值的平方；同时，u_ {k+1}+λ_ {1}u_ {k}可近似看作λ_ {1}的特征向量，同理u_ {k+1}+λ_ {2}u_ {k}也可近似看作λ_ {2}的特征向量。

易证该方法对于规范化后的向量序列也具有相同的收敛性，在此不额外给出证明。

在实际编程实现算法时，为尽可能地节省算力与内存并提高计算效率，我们不会预先求取最大迭代次数内每一次迭代的结果再将其分为两个向量序列判断其是否收敛（相邻向量插值小于设定误差限），而是需要结合上述改进算法与逐步迭代过程，对于每一次迭代的求解过程进行逻辑优化，优化后的逻辑如下所示（u_k代表规范化后的迭代向量序列，采用2范数方式进行规范化，k=1,2,…）：

• 若
  $$
  \left|\frac{\left(\boldsymbol{u}_{k+2}^{(1)}\right)_i}{\left(\boldsymbol{u}_k^{(1)}\right)i}-\frac{\left(\boldsymbol{u}{k+1}^{(1)}\right)i}{\left(\boldsymbol{u}{k-1}^{(1)}\right)_i}\right|<\varepsilon:,

  \left|\frac{\left(\boldsymbol{u}_{k+2}^{(1)}\right)i}{\left(\boldsymbol{u}{k+1}^{(1)}\right)i}-\frac{\left(\boldsymbol{u}{k+1}^{(1)}\right)_i}{\left(\boldsymbol{u}_k^{(1)}\right)i}\right|<\varepsilon:
  $$
  则取矩阵按模最大特征值
  $$
  \lambda_1=\frac{(\boldsymbol{u}{k+2}^{(1)})i}{(\boldsymbol{u}{k+1}^{(1)})i}
  $$
  对应的特征向量
  $$
  x_1=u{k+2}^{(1)}
  $$

• 若
  $$
  \left|\frac{\left(\boldsymbol{u}_{k+2}^{(1)}\right)_i}{\left(\boldsymbol{u}_k^{(1)}\right)i}-\frac{\left(\boldsymbol{u}{k+1}^{(1)}\right)i}{\left(\boldsymbol{u}{k-1}^{(1)}\right)_i}\right|<\varepsilon:,

  \left|\frac{(\boldsymbol{u}{k+2}^{(1)})i}{(\boldsymbol{u}{k+1}^{(1)})i}-\frac{(\boldsymbol{u}{k+1}^{(1)})i}{(\boldsymbol{u}k^{(1)})i}\right|>\varepsilon:
  $$
  则取矩阵按模最大特征值
  $$
  \lambda_1=\pm\sqrt{\frac{(\boldsymbol{u}{k+2}^{(1)})i}{(\boldsymbol{u}{k}^{(1)})i}}
  $$
  对应的特征向量
  $$
  x_1=\frac{u{k+2}^{(1)}+\lambda_1u{k+1}^{(1)}}{\parallel u{k+2}^{(1)}+\lambda_1u{k+1}^{(1)}\parallel_2}
  $$

基于以上的算法原理，可以编写如下MATLAB程序，实现矩阵按模最大特征值及其对应特征向量求解的改进算法，以解决矩阵按模最大特征值可能为一对相反数的特殊情况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

function calculatePowerMethod1(matrixEdit, iterEdit, fig)
    % 获取用户输入的矩阵matrixEdit和最大迭代次数iterEdit
    A = str2num(matrixEdit.Value); % 将字符串转换为矩阵
    n = length(A);
    V = rand(n,1);  % 以随机方式初始化迭代向量u0
    max_iter = iterEdit.Value;    % 获取迭代次数

    Eps = 1E-4; % 迭代精度
    k = 0; % 初始迭代次数

    % 乘幂法迭代，求得矩阵按模最大特征值lambda及其对应特征向量v
    while k <= max_iter - 1
        v = A * V;
        v1 = A * v;
        v_2 =norm(v, 2);
        minus1 = A * v1 ./ v - v1 ./ V;
        minus2 = A * v1 ./ v1 - v1 ./ v;
        if max(abs(minus1(:))) < Eps
            if max(abs(minus2(:))) < Eps
                lambda0 = A * v1 ./ v1;
                lambda = max(lambda0(:));
                v2_2 = norm(A * v1, 2);       
                v = A * v1 / v2_2;
            else
                lambda0 = A * v1 ./ v;
                lambda = sqrt(max(lambda0(:)));
                v3 = A * v1 + lambda * v1;
                v3_2 = norm(v3, 2);
                v = v3 / v3_2;
            end
            k = k + 1;
            break;
        end
        k = k + 1;
        V = v / v_2;
        lambda0 = A * v1 ./ v1;
        lambda = max(lambda0(:));
    end
end

求实对称矩阵的全部特征值

我们知道，实对称矩阵的不同特征值对应的特征向量一定是正交的，因此，可以通过幂法迭代得到矩阵的主特征值λ_ 1和主特征向量x_ 1 ，再重新给出一个新的与v_ 0线性无关的初始迭代向量v_ 1，使v_ 1和x_ 1正交化， 则可以由幂法迭代出矩阵的特征值λ_ 2和特征向量x_ 2。同样使新给出的初始迭代向量v_ 3和x_ 1、x_ 2正交 化，则可以由幂法得到λ_ 3和x_ 3。以此类推，可以计算出矩阵的全部特征值和特征向量。具体证明过程详见参考文献[3]，这里仅给出基于上述改进算法的完整算法逻辑：

令
$$
A_j=\mathbf{A}{j-1}-\lambda{j-1}\boldsymbol{x}{j-1}\boldsymbol{x}{j-1}^{\mathrm{T}}(j=2,3,\cdots n)
$$
采取与先前完全相同的迭代向量序列构造方式，有如下判断逻辑（u_k代表规范化后的迭代向量序列，采用2范数方式进行规范化，k=1,2,…）：

• 若
  $$
  \left|\frac{(u_{k+2}^{(j)})i}{(u_k^{(j)})i}-\frac{(u{k+1}^{(j)})i}{(u{k-1}^{(j)})i}\right|<\varepsilon:,\quad\left|\frac{(u{k+2}^{(j)})i}{(u{k+1}^{(j)})i}-\frac{(u{k+1}^{(j)})i}{(u_k^{(j)})i}\right|<\varepsilon:,
  $$
  且满足
  $$
  {|x{m}^{\mathrm{T}}v{k+2}^{(j)}|<\varepsilon}\left(m=1,2,\cdots,j-1\right)
  $$
  则取矩阵按模最大特征值
  $$
  {\lambda{j}}=\frac{\left(\boldsymbol{u}{k+2}^{(j)}\right){i}}{\left(\boldsymbol{u}{k+1}^{(j)}\right){i}}
  $$
  对应的特征向量
  $$
  x_{j}=\boldsymbol{u}_{k+2}^{(j)}
  $$

• 若
  $$
  \left|\frac{(u_{k+2}^{(j)})i}{(u_k^{(j)})i}-\frac{(u{k+1}^{(j)})i}{(u{k-1}^{(j)})i}\right|<\varepsilon:,\quad\left|\frac{(u_{k+2}^{(j)})_i}{(u_{k+1}^{(j)})_i}-\frac{(u_{k+1}^{(j)})_i}{(u_k^{(j)})_i}\right|>\varepsilon:,
  $$
  且满足
  $$
  \left|\boldsymbol{x}{m}^{\mathrm{T}}\frac{\boldsymbol{u}{k+2}^{(j)}+\lambda_{j}\boldsymbol{u}{k+1}^{(j)}}{\parallel\boldsymbol{u}{k+2}^{(j)}+\lambda_{j}\boldsymbol{u}{k+1}^{(j)}\parallel{2}}\right|<\varepsilon\quad(m=1,2,\cdots,j-1)
  $$
  则取矩阵按模最大特征值
  $$
  \lambda_{j}=\pm\sqrt{\frac{(\boldsymbol{u}{k+2}^{(j)}){i}}{(\boldsymbol{u}{k}^{(j)}){i}}}
  $$
  对应的特征向量
  $$
  \quad x_{j}=\frac{\boldsymbol{u}{k+2}^{(j)}+\lambda{j}\boldsymbol{u}{k+1}^{(j)}}{\parallel\boldsymbol{u}{k+2}^{(j)}+\lambda_{j}\boldsymbol{u}{k+1}^{(j)}\parallel{2}}
  $$

基于以上的算法原理，可以编写如下MATLAB程序，实现矩阵按模最大特征值及其对应特征向量求解的改进算法，并对于实对称矩阵的全部特征值进行依次求解（每次运行该函数进行一个特征值的求解，代码中省去了存储用于求解下一个特征值的矩阵作为全局变量的部分）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

function calculatePowerMethod2(iterEdit, fig)
    % 从存储的全局变量中读取需要求解主特征值的新矩阵data.matrix
    A = data.matrix; % 将字符串转换为矩阵
    n = length(A);
    V = rand(n,1); 
    max_iter = iterEdit.Value;    % 获取迭代次数

    Eps = 1E-4; % 迭代精度
    k = 0; % 初始迭代次数

    % 乘幂法迭代，求得矩阵按模最大特征值lambda及其对应特征向量v
    while k <= max_iter - 1
        v = A * V;
        v1 = A * v;
        v_2 =norm(v, 2);
        v2_2 = norm(A * v1, 2);
        v2 = A * v1 / v2_2;
        lambda0 = A * v1 ./ v;
        lambda = sqrt(max(lambda0(:)));
        v3 = A * v1 + lambda * v1;
        v3_2 = norm(v3, 2);
        minus1 = A * v1 ./ v - v1 ./ V;
        minus2 = A * v1 ./ v1 - v1 ./ v;
        if max(abs(minus1(:)))<Eps
            num1 = 0;
            num2 = 0;
            for l = 1 : j
                x = full_V(:,l);
                if max(abs(minus2(:))) < Eps && abs(x' * v2) < Eps
                    num1 = num1 + 1;
                elseif max(abs(minus2(:))) > Eps && abs(x' * v3 / v3_2) < Eps
                    num2 = num2 + 1;
                end
            end
            if num1 == j
                lambda0 = A * v1 ./ v1;
                lambda = max(lambda0(:));
                v = A * v1 / v2_2;
                k = k + 1;
                break;
            elseif num2 == j
                lambda0 = A * v1 ./ v;
                lambda = sqrt(max(lambda0(:)));
                v = v3 / v3_2;
                k = k + 1;
                break;
            end
        end
        k = k + 1;
        V = v / v_2;
        lambda0 = A * v1 ./ v1;
        lambda = max(lambda0(:));
    end
end

数据测试实验

针对以上提到的乘幂法及其改进算法，将其MATLAB求解代码整合进GUI中，并对求解过程中矩阵按模最大特征值随迭代次数增加的收敛情况进行可视化，基本界面如下：

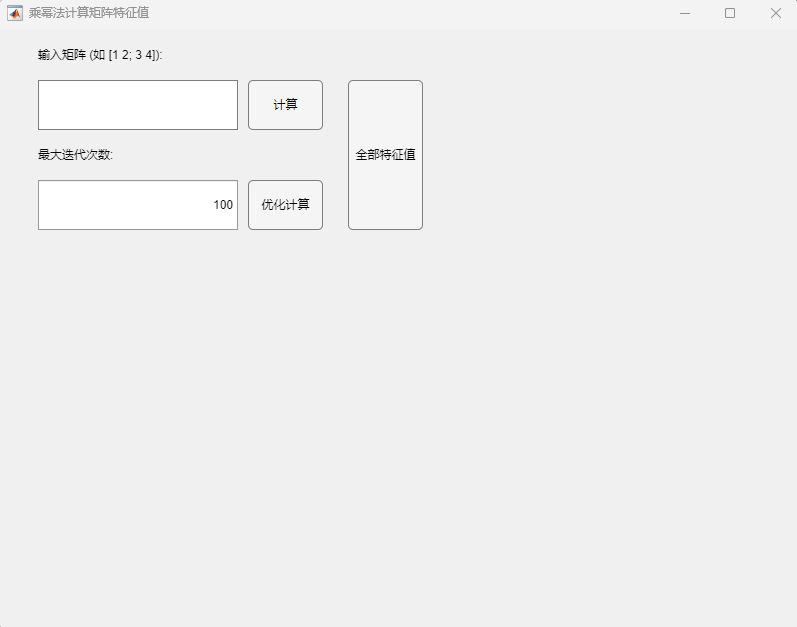
乘幂法基础算法

将待求解的矩阵按照格式要求输入框体内，并指定最大迭代次数（默认为100次），按下“计算”控件可以利用基础的乘幂法（归一化版本）对矩阵按模最大特征值及其对应特征向量进行求解，同时会调用MATLAB中自带的矩阵特征值求解函数eig()对求解结果进行验证。

例：矩阵（特征值为-1、3、5）

$$
A=\begin{pmatrix}1&-1&2\-2&0&5\6&-3&6\end{pmatrix}
$$

程序求解与可视化结果：

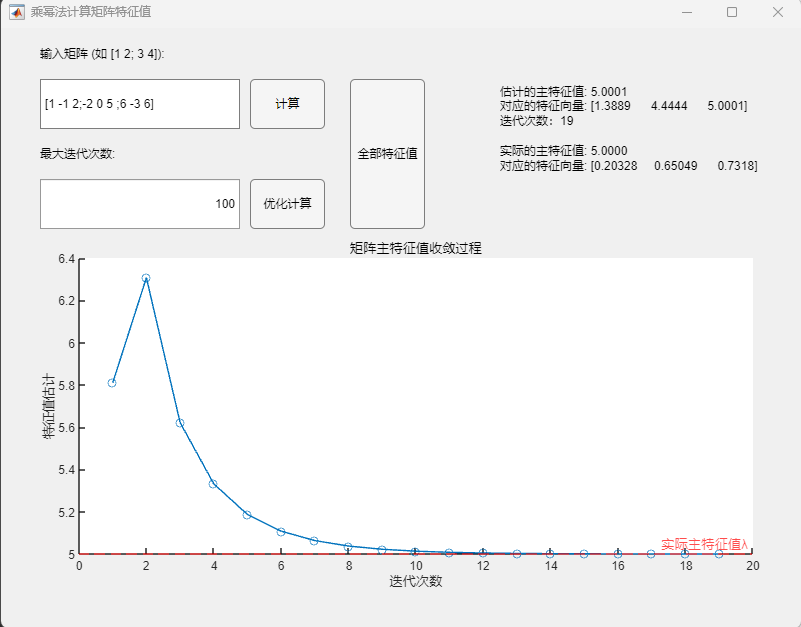
可以发现，估计的主特征值与实际的主特征值在限定的精度内基本一致，对应的特征向量相差了相同的倍数，也可视为正确求解。

乘幂法改进算法

将待求解的矩阵按照格式要求输入框体内，并指定最大迭代次数（默认为100次），按下“优化计算”控件可以利用改进的乘幂法（归一化版本）对矩阵按模最大特征值及其对应特征向量进行求解，同时会调用MATLAB中自带的矩阵特征值求解函数eig()对求解结果进行验证。

例1：矩阵（特征值为-1、3、5）

$$
A=\begin{pmatrix}1&-1&2\-2&0&5\6&-3&6\end{pmatrix}
$$

程序求解与可视化结果：

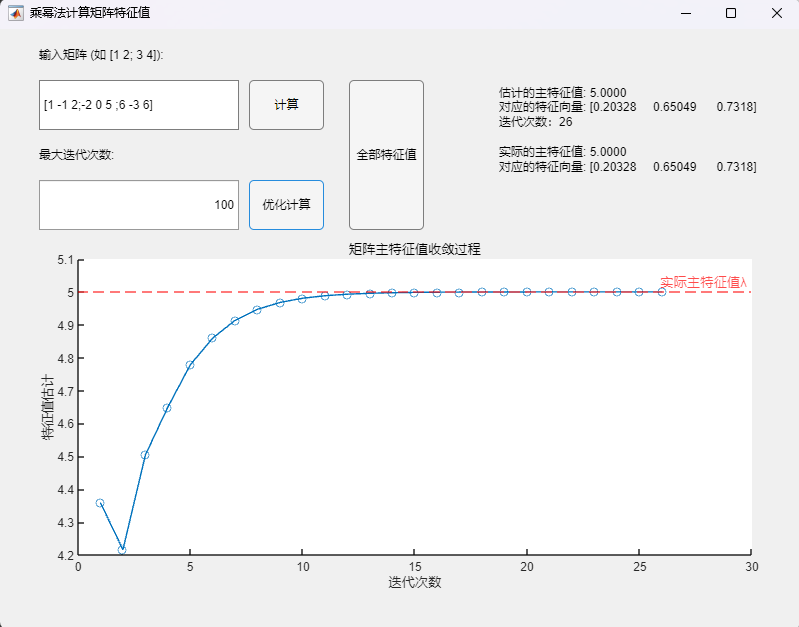
可以发现，估计的主特征值与实际的主特征值在限定的精度内保持一致，通过该算法计算得到的对应特征向量也与MATLAB自带函数（基于 Cholesky 分解/QR分解方法的特征值求解）的求解结果在限定精度内完全一致，但计算需要的迭代次数较基础算法而言有明显增加。

例2：矩阵（特征值为3、-3、1，按模最大特征值为一对相反数）

$$
A=\begin{pmatrix}3&-2&4\0&-3&2\0&0&1\end{pmatrix}
$$

程序求解与可视化结果：

调用乘幂法基本算法：

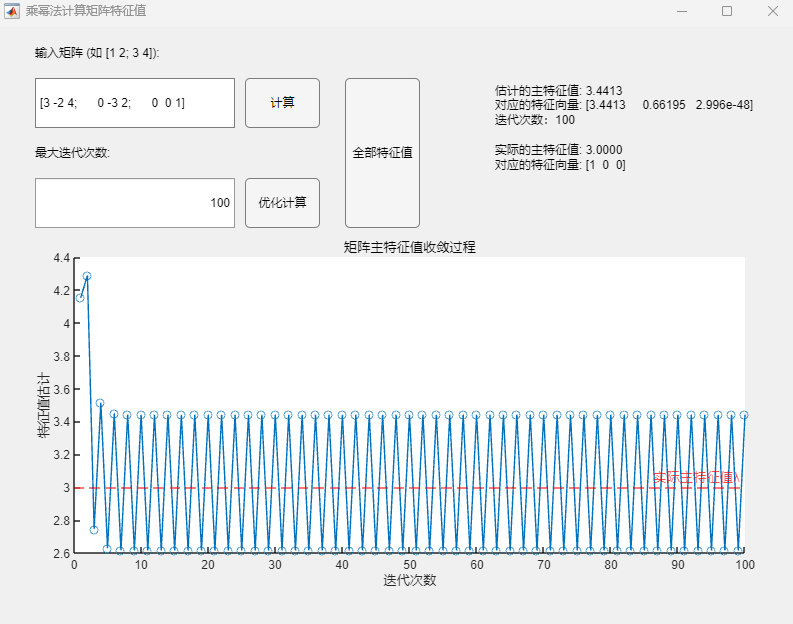
调用乘幂法改进算法：

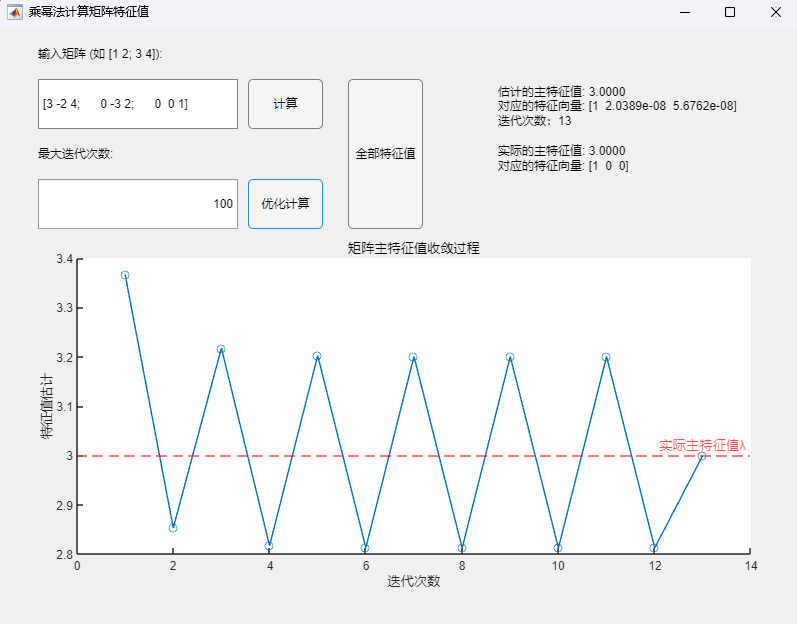
可以发现：

• 调用基础算法时，迭代向量序列在设定的最大迭代次数内并不收敛，最终的求解结果也与实际按模最大特征值有较大误差；
• 而调用改进算法时，尽管从主特征值收敛过程的可视化结果中无法确定向量序列的收敛性（实际上原序列仍发散），但序列中的向量一隔一选取构成的新序列（图像中对应迭代次数全为奇数/偶数的震荡单边）已由程序判断收敛，且估计的主特征值与实际的主特征值在限定的精度内保持一致，通过该算法计算得到的对应特征向量也与MATLAB自带函数（基于 Cholesky 分解/QR分解方法的特征值求解）的求解结果在限定精度内完全一致。

例3：3阶矩阵（特征值为3（重根），但不具有3个线性无关的特征向量）

$$
A=\begin{pmatrix}3&1&0\0&3&1\0&0&3\end{pmatrix}
$$

程序求解与可视化结果：

调用乘幂法基本算法（最大迭代次数100）：

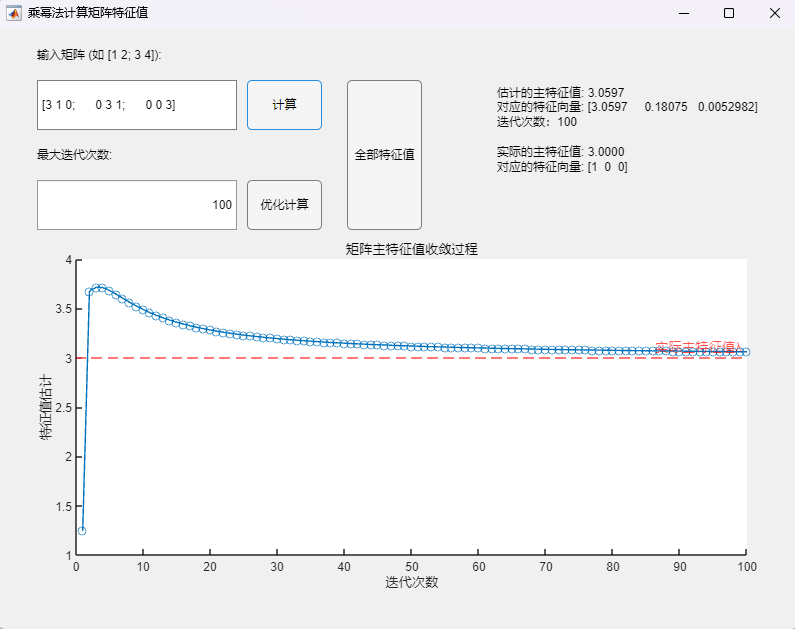
调用乘幂法改进算法（最大迭代次数100）：

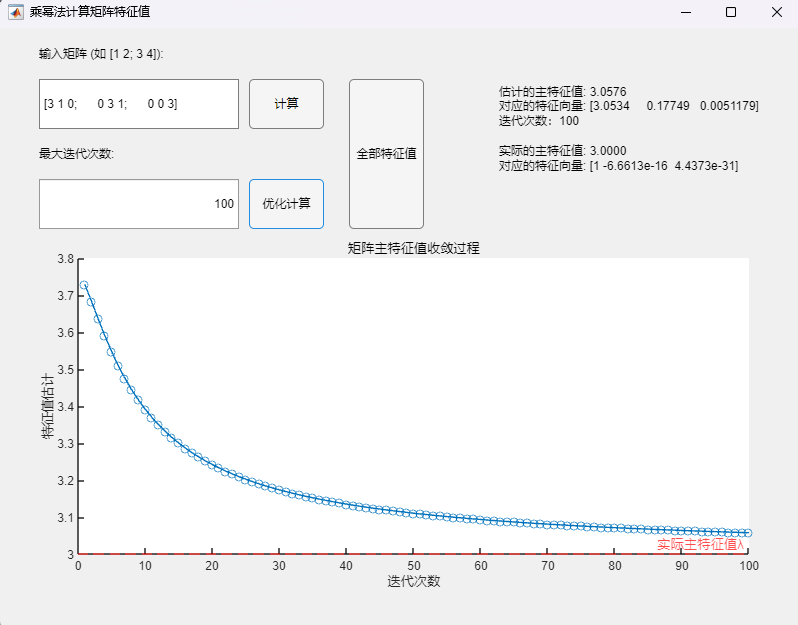
调用乘幂法基本算法（最大迭代次数10000）：

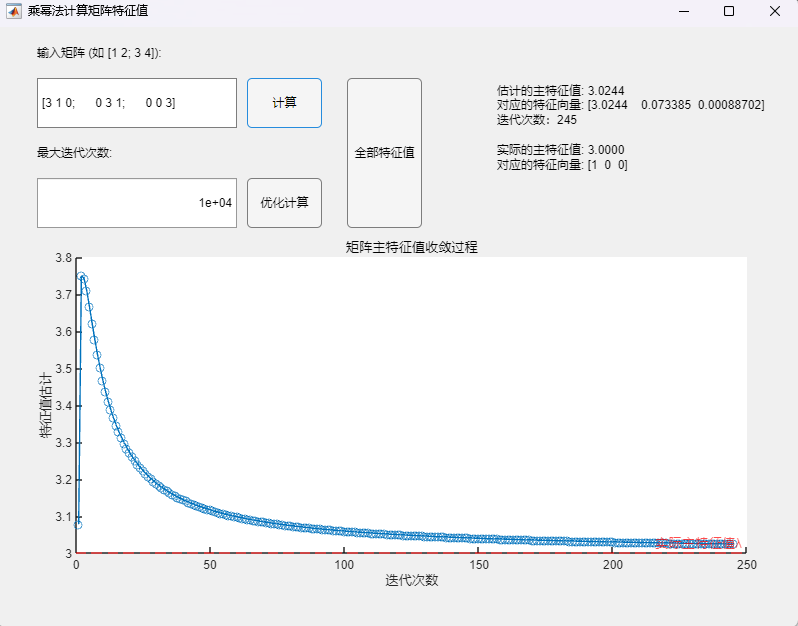
调用乘幂法改进算法（最大迭代次数10000）：

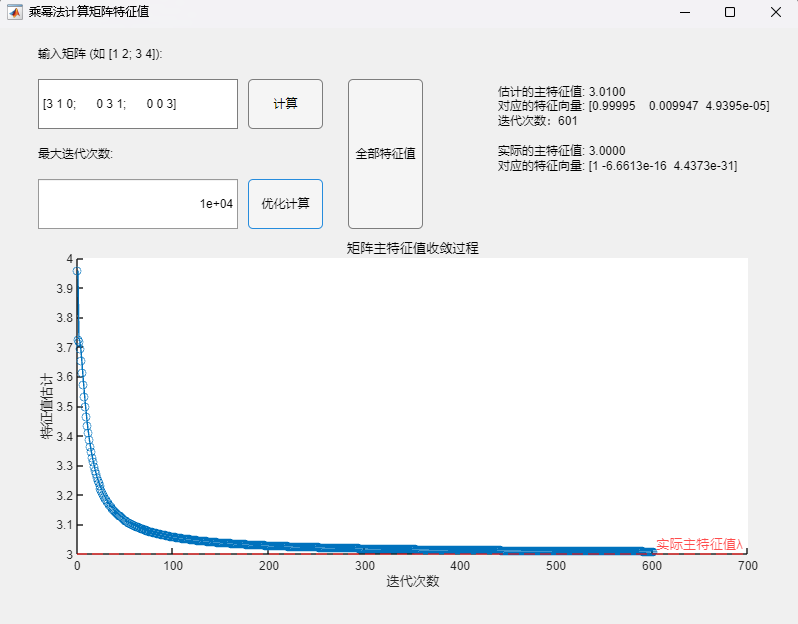
可以发现，当矩阵不具有n个线性无关的特征向量时，乘幂法从理论上讲不再适用（不满足假设条件），但实际测试可以发现：

• 当最大迭代次数设置较小（100）时，两种方法均未呈现数值上的收敛（两次迭代间误差不超过设定误差限10^(-4)），所求得的主特征值与对应特征向量与真实值之间均有明显误差；
• 当最大迭代次数设置足够大（10000）时，两种方法在迭代次数达到10^2数量级时实现了数值上的收敛（两次迭代间误差不超过设定误差限10^(-4)），但在停止迭代后，通过乘幂法基础算法求得的主特征值与对应特征向量与真实值之间仍有明显误差，而通过改进算法求得的主特征值与对应特征向量与真实值已经基本接近，但改进算法所需要的迭代次数也明显更多。

但总的来说，从理论角度出发，在这种情况下乘幂法已不再适用，本例的情况仅为收敛较慢，此时改进算法相较于基础算法有更好的精度；但也会有不收敛的情况，此时两种方法均会有比较大的误差，而这是无法事先判断的，因此在使用乘幂法时还是尽量避免该种情况，或者说在优化算法仍然无法快速收敛的情况下需要注意到矩阵不具有n个线性无关的特征向量的特殊情况，此时应选取其他合适的特征值求解算法。

例4：矩阵（特征值为1+2i、1-2i、0.5，按模最大特征值为一对共轭复数）

$$
A=\begin{pmatrix}1&-2&0\2&1&0\0&0&0.5\end{pmatrix}
$$

程序求解与可视化结果：

调用乘幂法基本算法：

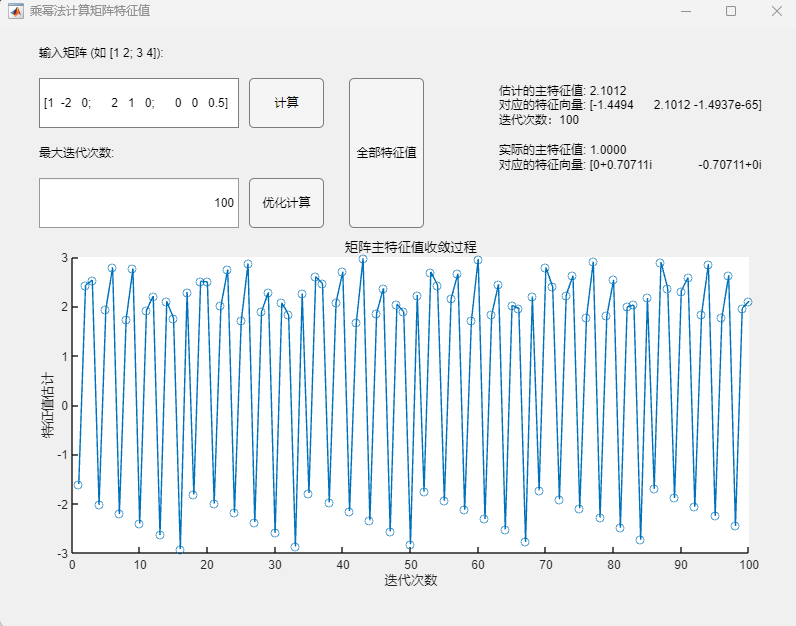
调用乘幂法改进算法：

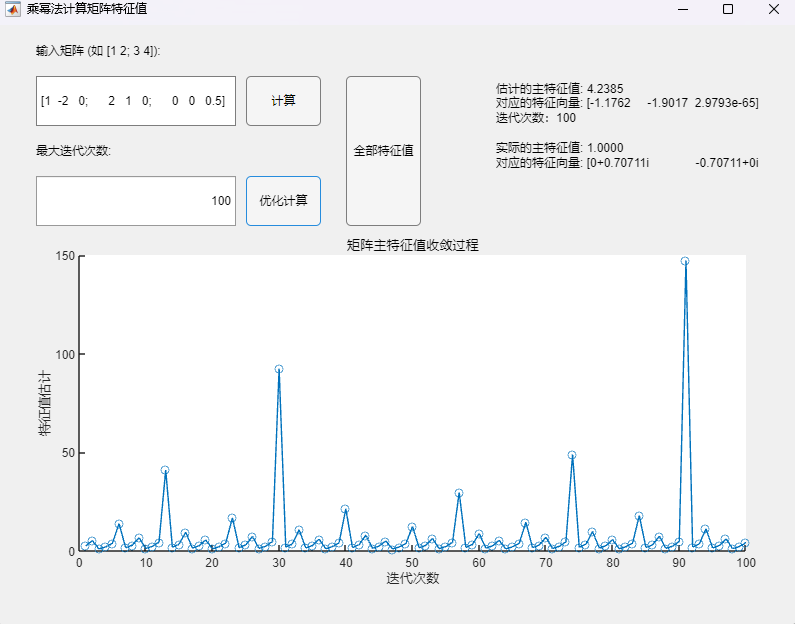
此情况下两种乘幂法均呈现了极大的不稳定性，无法正确求解。

求实对称矩阵的全部特征值

例1：矩阵（特征值为-1、3、5）

$$
A=\begin{pmatrix}1&-1&2\-2&0&5\6&-3&6\end{pmatrix}
$$

程序求解与可视化结果：

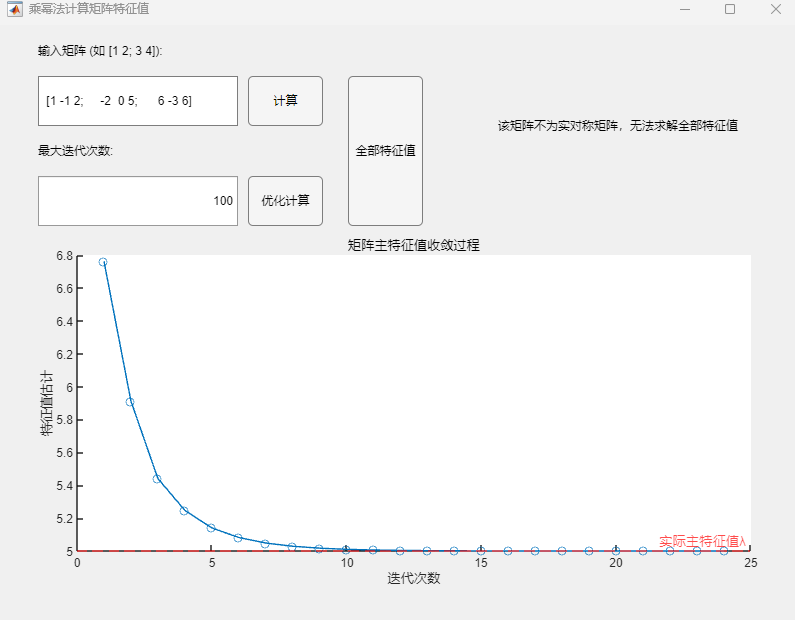
该矩阵不为对称矩阵，无法通过上述算法实现全部特征值的求解，为排错示例。

例2：对称矩阵（特征值为1、2、4）

$$
A=\begin{pmatrix}3&1&1\1&2&0\1&0&2\end{pmatrix}
$$

程序求解与可视化结果：

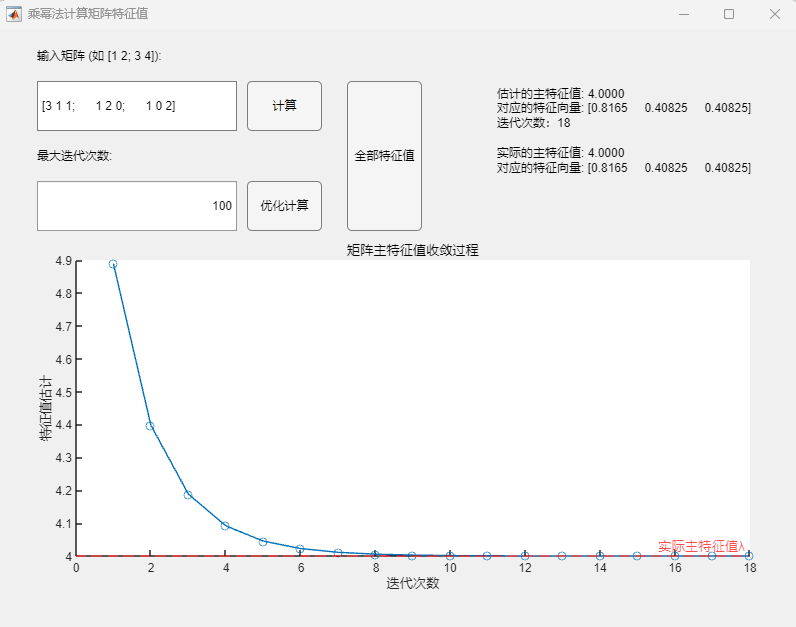
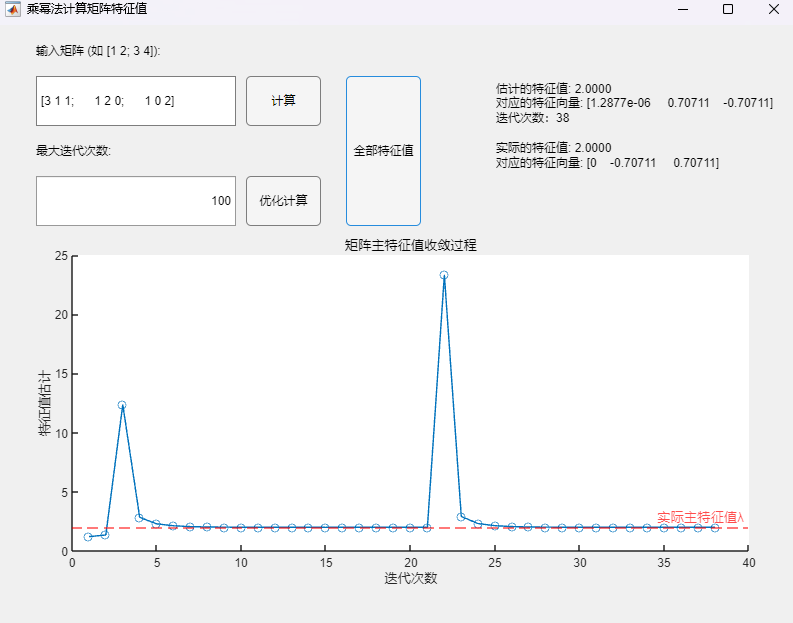
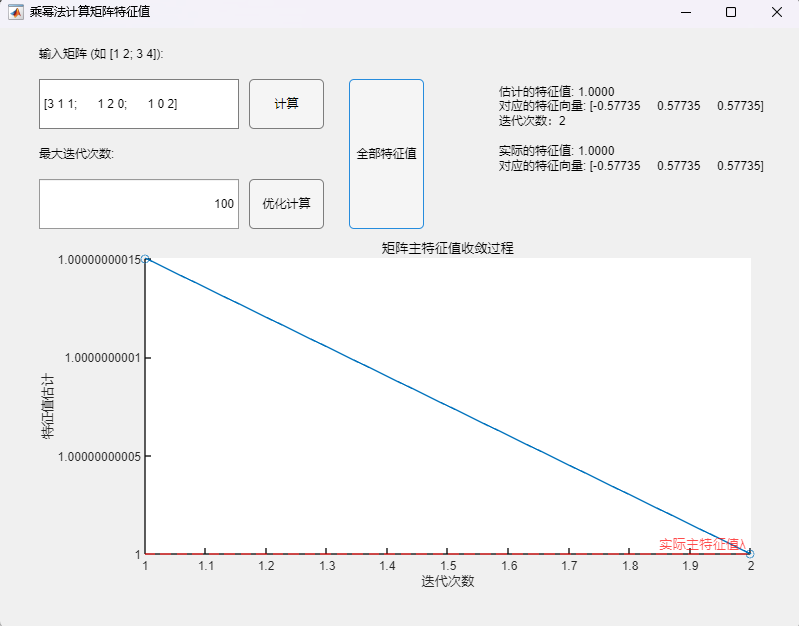
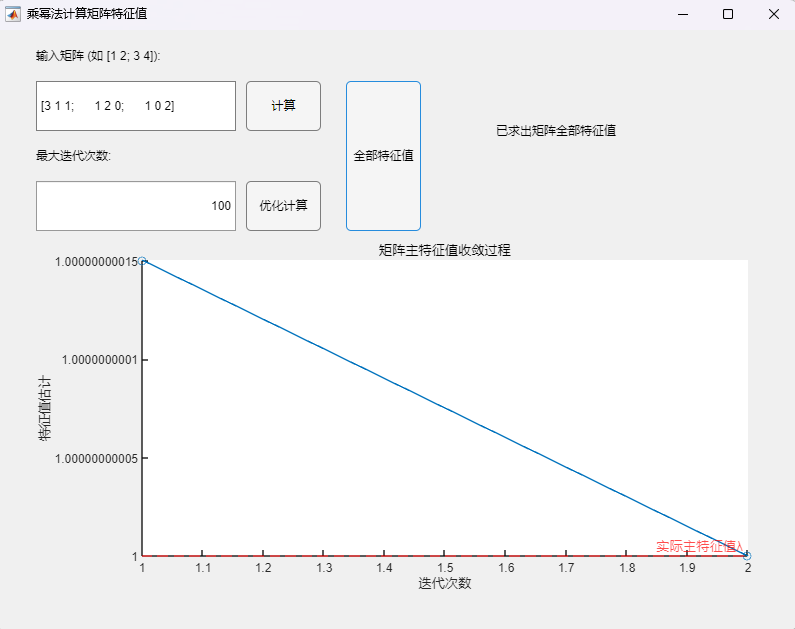
可以看到，该算法可以用于正确求取实对称矩阵的所有特征值及其相应的特征向量，求解结果与MATLAB自带函数（基于 Cholesky 分解/QR分解方法的特征值求解）的求解结果在限定精度内完全一致。

例3：对称矩阵（特征值为2、1、-1）

$$
A=\begin{pmatrix}1&1&0\1&0&1\0&1&1\end{pmatrix}
$$

程序求解与可视化结果：

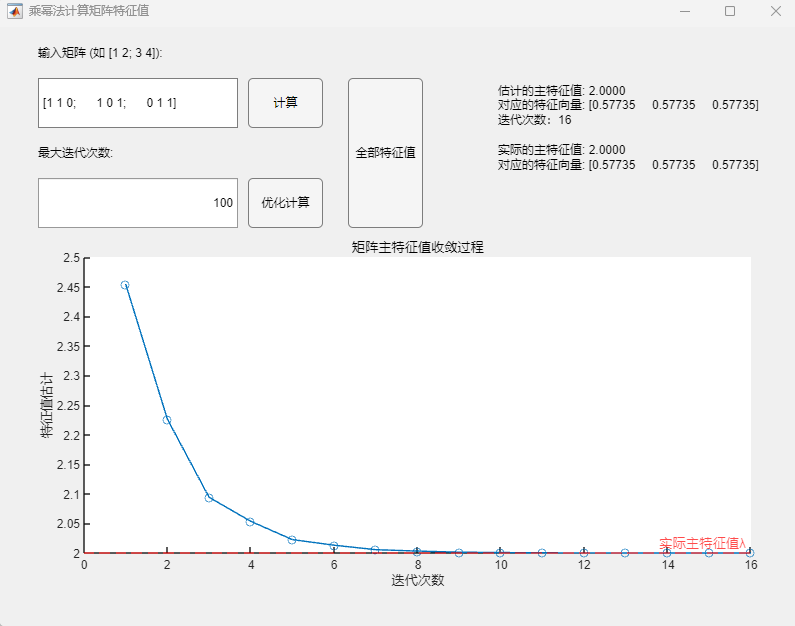
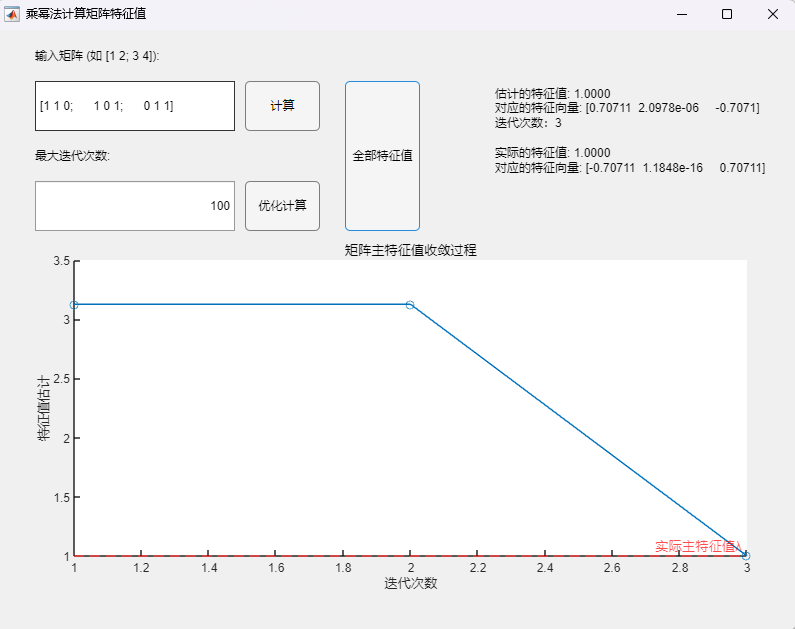
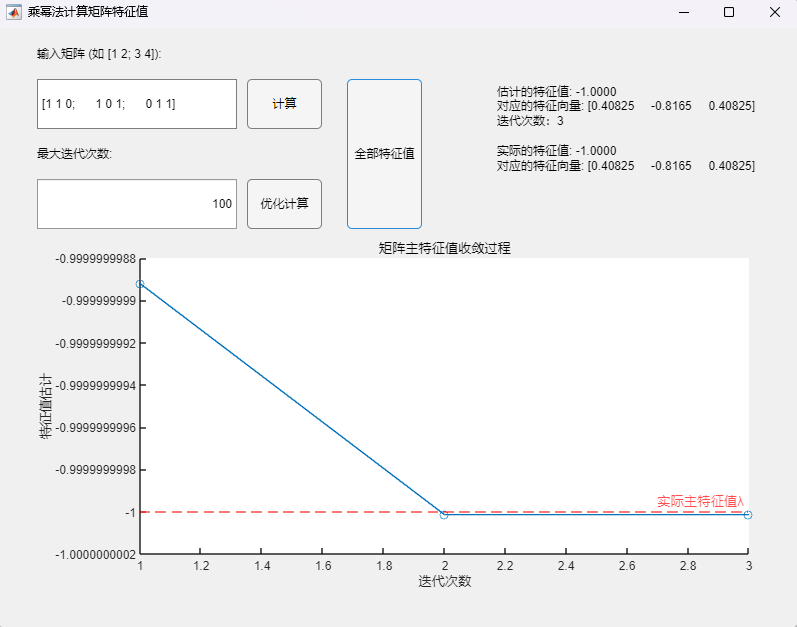
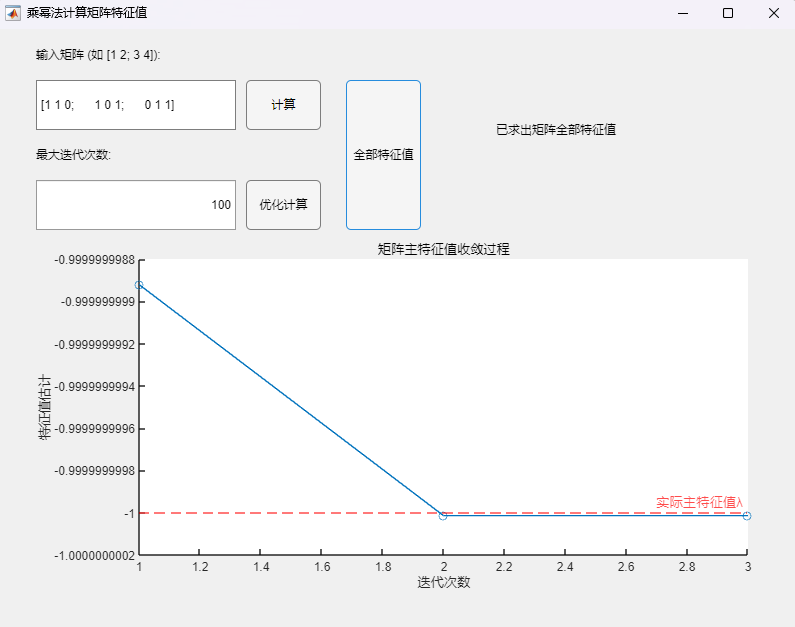
可以看到，即使在矩阵的次主特征值为一对相反数的情况下，该算法也可以用于正确求取实对称矩阵的所有特征值及其相应的特征向量，求解结果与MATLAB自带函数（基于 Cholesky 分解/QR分解方法的特征值求解）的求解结果在限定精度内完全一致。

参考文献

[1] 王开荣,杨大地编著.应用数值分析[M].高等教育出版社,2010.

[2] 曹连英,曲智林,杨瑞智.基于幂法的求实对称矩阵特征值的注记[J].大学数学,2024,40(04):67-72.

[3] 曾莉,肖明.计算实对称矩阵特征值特征向量的幂法[J].南昌大学学报(理科版),2016,40(04):399-402.

[4] 张青,苟国楷,吕崇德.乘幂法的改进算法[J].应用数学与计算数学学报,1997,(01):51-55.

[5] 马志勇,方珑.矩阵特征值求解及其在图像压缩中的应用[J].上海第二工业大学学报,2012,29(04):315-318.

摘要

本项目的核心任务是通过统计过程控制（SPC）方法，对某工厂生产的滚珠直径数据进行产品质量管理，评估产品工艺水平及其生产过程是否受控。统计过程控制作为一种基于概率统计的过程控制方法，自1924年由Shewhart博士提出控制图以来，已广泛应用于现代制造过程的质量控制中。本项目基于Matlab软件开发，对于收集到的数据，通过描述性统计分析、正态性检验、总体均值检验、工序能力指数计算与绘制均值控制图和方差控制图等多种方式，对数据进行全面分析，最终评估工艺水平及生产过程的受控状态。具体而言，首先，在数据收集过程中，结合实际数据与模拟数据，得到25组产品质量样本数据（每组至少5个样本）；随后，通过描述性统计分析方法对数据进行宏观的认知，根据均值、方差、极差、直方图等指标对数据进行初步分析；接着又利用假设检验的方法，分别通过Pearson卡方检验与t检验等方法验证数据是否符合正态分布，并对其总体均值进行检验。基于对于正态总体及其均值、方差的检验合理性，最终计算并评估了数据的工序能力指数，同时绘制了均值控制图和方差控制图，以直观反映生产过程中的数据波动情况。通过多种方法的综合分析，最终得出了工厂生产的滚珠直径的工艺水平评价和生产过程的受控状态判断。

关键词: 产品质量管理、统计过程控制（SPC）、假设检验、Shewhart控制图、Matlab

项目概述

问题背景

现代产品质量管理主要有两个核心目标：第一，评价产品的工艺水平如何，即产品质量如何；第二，评价产品的生产过程是否受控，即产品可靠性如何。从现代质量控制的角度看，一方面要求产品质量好，另一方面还要求可靠性高。

统计过程控制(Statistical Process Control, SPC)是一种基于概率统计的过程控制方法。1924年美国贝尔实验室的Shewhart博士提出控制图，标志着产品统计质量控制的正式起点。作为现代质量管理的重要方法，SPC广泛应用于现代制造过程的质量控制。20实际80年代，国际上半导体制造过程已经普遍采用SPC技术提升产品合格率和可靠性。比如Motorola公司提出并在美国通用电器公司等广泛应用的6σ管理，其主要技术基础就是SPC理论。

生产过程是否处于统计受控状态，取决于生产过程是否存在异常因素导致产品质量的起伏变化。产品加工结果是否满足加工规范要求，反应的是工艺水平的高低；而工艺是否受控，反应的是生产过程是否存在异常因素。

项目任务

在本次项目中，需要收集批量产品质量数据，利用SPC方法对其进行管理，分析整体工艺水平并判断生产过程是否处于统计受控状态，具体而言可细分为如下任务：

• 任务 1:收集或生成25组以上的数据，每组至少5个样本。

• 任务2:根据均值，方差，极差，直方图等指标，对数据进行描述性统计分析。

• 任务 3:对数据进行正态性检验与总体的均值检验。

• 任务 4:计算数据工序能力指数并对其进行评估。

• 任务 5:描绘均值控制图和方差控制图。

• 任务 6:得出结论：工艺水平如何；生产过程是否处于统计受控状态。

项目过程

本项目完全基于Matlab代码实现SPC方法进行产品质量管理。

数据收集

本项目中的数据收集采用实际数据与模拟数据结合的方式，其中实际数据以书本7.4节的例题7.4.4[^1]为主要来源，在此基础上利用生成的模拟数据对其进行扩充，最终得到25组产品质量样本数据，每组中含有5个数据。

具体而言，本项目的问题情境为对工厂生产的滚珠直径（单位：$mm$）进行产品质量管理。书本上的例题提供了50个直径数据，将其作为扩充生成模拟数据的源数据source_data，即：

1
2
3
4
5
6
7
8
9
10

source_data=[15.0,15.8,15.2,15.1,15.9,
             14.7,14.8,15.5,15.6,15.3,
             15.0,15.6,15.7,15.8,14.5,
             15.1,15.3,14.9,14.9,15.2,
             15.9,15.0,15.3,15.6,15.1,
             14.9,14.2,14.6,15.8,15.2,
             15.2,15.0,14.9,14.8,15.1,
             15.5,15.5,15.1,15.1,15.0,
             15.3,14.7,14.5,15.5,15.0,
             14.7,14.6,14.2,14.2,14.5]; 

设置扩充后的数据组数num_groups以及各组样本数据个数samples_per_groups：

1
2

num_groups = 25;
samples_per_group = 5;

两者相乘得到样本数据总数num_data_points：

1

num_data_points = num_groups * samples_per_group;

要对原始数据进行扩充，首先需要复制原始数据并添加随机扰动：

1
2

replicated_data = repmat(source_data, 1, ceil(num_data_points / length(source_data)));
perturbed_data = replicated_data(1:num_data_points) + 0.05 * randn(1, num_data_points);

接着使用插值生成更多数据点，并保留一位小数：

1
2
3
4

x = 1:length(perturbed_data);
xi = linspace(1, length(perturbed_data), num_data_points);
interpolated_data = interp1(x, perturbed_data, xi, 'spline');
interpolated_data = round(interpolated_data, 1);

最后将生成的模拟数据点重新组织为25组，每组5个数据，得到完整样本数据：

1
2

expanded_data = reshape(interpolated_data, samples_per_group, num_groups)';
data = expanded_data;

最终的样本数据如下表所示：

其中每行表示一组数据，共25组，每组中有5个数据。

描述性统计分析

描述性统计量主要有以下几种：

• 均值 (Mean): 计算每组数据的平均值，反映该组数据的中心位置。

• 方差 (Variance): 度量数据分散程度，数值越大表示数据的波动越大。

• 标准差 (Standard Deviation): 方差的平方根，同样反映数据的分散程度，但单位与数据相同。

• 极差 (Range): 最大值与最小值的差，表示数据的跨度。

利用Matlab软件中自带的库函数，可以分别实现对于各组数据均值、方差、标准差与极差等统计量的计算：

1
2
3
4

means = mean(data, 2); 
variances = var(data, 0, 2); 
ranges = range(data, 2); 
stds = std(data, 0, 2);

以及计算总体数据的均值、方差、标准差与极差：

1
2
3
4

overall_mean = mean(data(:)); 
overall_variance = var(data(:)); 
overall_range = range(data(:)); 
overall_std = std(data(:));

值得注意的是，Matlab中计算方差的函数 var(A) 默认会按照 N-1（N是观测值数量，即上文中的num_data_points）实现归一化，从而可以作为对于总体分布的方差的无偏估计。上述得到的均为修正后的样本方差。

通过对于上述四个描述性统计量的样本观测结果进行初步分析，可以得到如下结论：

• 滚珠直径的总体平均值约为15.1mm，可作为后续总体均值检验的检验目标。

• 各组数据的方差均在0.5以内，总体方差与标准差也较低，说明生产过程中数据波动较小，产品质量稳定性较高。

• 数据极差范围适中，总体极差不超过2，处于合理区间。

除此之外，还可以通过绘制频数分布直方图的方式对于样本数据进行描述性统计分析：

1

h = histogram(data);

观察图表可知，数据的频数分布大致呈”两边少，中间多”的趋势，推测其总体大致服从正态分布，需要进行进一步检验。

数据正态性检验

要验证总体是否服从正态分布，需要采用Pearson卡方检验方法，对总体的分布类型进行检验。

Matlab软件中，有相应的函数chi2gof可通过Pearson卡方检验来验证总体分布类型是否为正态分布：

1

[result, p_chi2] = chi2gof(data(:));

chi2gof函数是使用Pearson卡方检验返回原假设的检验决策，其原假设假定样本数据来自正态分布的总体，备择假设是样本数据不来自正态分布的总体。默认情况（仅将样本数据data输入chi2gof函数）下，检验的显著性水平为δ=0.05，且默认检验总体是否服从正态分布；通过增加函数的输入参数可以对显著性水平和检验的分布类型进行更改，在此不再赘述。

返回的参数result为正态性检验的结果，若result=0，说明无法拒绝原假设，即可认为样本数据来自正态分布的总体；若result=1，则拒绝原假设，认为数据不来自正态分布的总体。另一返回参数p_chi2则为该检验的p值，当其大于显著性水平δ时不拒绝原假设。

通过对样本数据进行正态性检验，可认为数据来自正态分布的总体，正态性检验的p值为0.37005。

从原理出发，也可根据假设检验的基本方法流程对总体的分布类型进行检验：

首先，提出原假设与备择假设：

• H_0：总体服从正态分布，即
  $$
  F(x) = \phi(\frac{x-\mu}{\sigma})
  $$

• H_1：总体不服从正态分布，即
  $$
  F(x) \neq \phi(\frac{x-\mu}{\sigma})
  $$

其中F(x)为总体的分布，μ和σ为正态分布的均值与方差（均为未知参数）。

接着，根据假设的提出给出对应的拒绝域形式：
$$
R_0 = \left{ T>c \right}
$$
其中T为构造的统计量：

$$
T=\sum_{i=1}^{r}\frac{ {(n_i-n{p}_i)}^2}{np_i}
$$
若将对总体X所有可能的取值范围分割成$r个两两不交的部分，则式中：

• n_i：统计样本中实际落入第i个部分的个数（实际频数）；
• n：样本数据总数，即上文代码中的num_data_points；
• p_i：任一样本落入第$i$个部分的概率。

显然，当原假设
$$
H_0: F(x) = \phi(\frac{x-\mu}{\sigma})
$$
成立时，理论频数n*p_i应与实际频数n_i较为接近，这也是拒绝域形式的确定依据。

可以注意到，Pearson卡方统计量
$$
T=\sum_{i=1}^{r}\frac{ { {(n_i-np}_i)}^2}{np_i}
$$
服从如下的大样本分布：

$$
\hat{T}=\sum_{i=1}^{r}\frac { { {(n_i-n\hat{p}}_i)}^2}{n{\hat{p} }_i}\rightarrow X^2(r-1-s)
$$
其中：

s表示待估未知参数的个数，显然本项目中s=2；

hat(p)_i为任一样本落入第i部分的概率p_i的估计值，这是由于假定的分布类型中含有未知参数，因此需要先根据样本数据对未知参数进行极大似然估计，再代入得到概率的估计值。

然后，需要计算犯第一类错误的概率
$$
\alpha=P \left{H_1|H_0\right} = \left{T>c|\F(x)=F_0(x)\right}
$$
并根据α = δ = 0.05求得拒绝域中未知参数c的临界值criticalValue = 11.0705：

1
2
3
4
5
6

deta=0.05;
mu_MLE = overall_mean;
sigma2_MLE = overall_variance*(num_data_points-1)/num_data_points; 
sigma_MLE = sqrt(sigma2_MLE);
dimension=numBins-1-2;
criticalValue = chi2inv(1 - deta, dimension);

事实上，上文中提到Matlab软件中的var(A)函数默认按照N-1实现归一化，而正态分布方差的极大似然估计应为未修正的样本方差，故特此进行更正；同时，在2.2节的描述性统计分析过程中，涉及到频数直方图的绘制时已经对数据完成了分组，可直接通过读取上述的图表属性获取分组数numBins（对应上文中r）、各组频数binCounts（对应上文中实际频数n_i与各分组边界binEdges（可用于计算p_i））：

1
2
3

numBins = h.NumBins;
binCounts = h.Values;
binEdges = h.BinEdges;

最后，通过样本数据计算出对应卡方统计量T的观测kafang = 2.6897：

1
2
3
4
5
6
7
8
9

kafang=0;
p_hat(1)= normcdf(binEdges(2), mu_MLE, sigma_MLE);
for i=2:numBins-1
    p_hat(i)= normcdf(binEdges(i+1), mu_MLE, sigma_MLE)-normcdf(binEdges(i), mu_MLE, sigma_MLE);
end
p_hat(numBins)= 1-normcdf(binEdges(numBins), mu_MLE, sigma_MLE);
for i=1:numBins
    kafang=kafang+(binCounts(i)-num_data_points*p_hat(i))^2 / (num_data_points*p_hat(i));
end

由于kafang<criticalValue，即不位于拒绝域内，因此无法拒绝原假设H_0，即可以认为数据确实来自正态分布的总体，与直接调用Matlab内置库函数的结果一致。

总体均值检验

通过Pearson卡方检验，已经可以认为在显著性水平δ=0.05的情况下，总体近似服从正态分布。进一步地，还希望对该正态总体的均值参数μ进行假设检验。在2.2节的描述性统计分析过程中，已经计算得到样本的总体均值（实际上也是正态分布参数μ的无偏估计与最大似然估计）μ_0 约为15.1(mm)，因此接下来的假设检验过程就将其作为检验对象：

1

miu0=15.1;

在正态总体的均值检验过程中，主要采取t检验的方法，即认为正态总体的另一参数σ未知。这样的检验方法的合理性是显然的，此时需要构造服从t分布的统计量以进行t检验。

在Matlab软件中，对于t检验仍然有相对应的库函数ttest()可以调用：

1

[result1, ttest_p_value] = ttest(data(:),miu0);

函数ttest(data(:),miu0)使用单样本t检验返回原假设的检验决策，其原假设假定数据data来自均值等于输入参数miu0且方差未知的正态分布，而备择假设是总体分布的均值不等于miu0。如果该检验在默认为5%的显著性水平上拒绝原假设，则函数的返回值result1为1，即认为正态总体的均值不为miu0，否则为0；而另一返回值ttest_p_value则为该检验的p值，当其大于显著性水平时不拒绝原假设，即可认为正态总体的均值等于miu0。

运行代码可得：正态总体均值检验p值ttest_p_value=0.8687，可认为正态总体的均值约为μ_0=15.1。

同样的，这样的假设检验过程也可以基于一般的统计方法实现：

首先，提出原假设与备择假设：

• H_0：正态总体的均值为15.1，即μ=μ_0=15.1；
• H_1：正态总体的均值不为15.1，即μ ≠ μ_0。

接着，根据假设的提出给出对应的拒绝域形式：
$$
R_0 = \left{ (x_1, x_2,…,x_n)^T :|\bar{x}-\mu_0| >c \right}
$$
该拒绝域形式的构造是具有合理性的，因为显然可证明样本均值bar{x}是对于正态总体参数μ的无偏估计，若原假设H_0成立，则说明bar{x}应与设定检验值μ_0较为接近，反之可得其拒绝域应描述为bar{x}与μ _0相距较远的情形，基于这样的原理也可构造其他形式的拒绝域，这里只是给出一种可能性。

然后，需要计算犯第一类错误的概率
$$
\alpha=P \left{H_1|H_0\right} = \left{\bar{x}-\mu_0| >c|\mu=\mu_0\right}
$$
并根据α = δ = 0.05求得拒绝域中未知参数c的临界值tcriticalValue = 0.0765：

1
2
3
4

deta=0.05;
dimension=num_data_points-1;
s=sqrt(var(data(:)));
tCriticalValue = tinv(1 - deta/2, dimension)*s/sqrt(num_data_points);

上述计算操作的依据是，在对第一类错误发生概率α的计算过程中，可以根据抽样分布定理构造出对应的t统计量
$$
\frac{\bar{x}-\mu_0}{s/\sqrt{n}} \sim t(n-1)
$$
从而查表进行计算求解得到临界值
$$
c=\frac{t_{1-\frac{\delta}{2}}(n-1)*s}{\sqrt{n}}
$$
其中s为样本数据的标准差（修正后），n为样本容量num_data_points。

最后，前文已经计算出样本均值为bar{x}，若将其与待检验值μ_0之间的距离|bar{x}-μ _0|定义为参数d，则在判定是否处于拒绝域中时只需要比较d与临界值tcriticalValue即可：

1

d=abs(overall_mean-miu0);

计算得到d=0.0064，小于临界值tcriticalValue = 0.0765，即不位于拒绝域内，因此无法拒绝原假设，可认为正态总体的均值μ约为15.1。这同样与直接调用Matlab内置函数的结果相一致。事实上，只要μ_0在样本均值bar{x}=15.1064上下tcriticalValue = 0.0765的区间范围内，都可在显著性水平δ=0.05的情况下认为是正态总体的均值μ。

数据工序能力指数的计算与评估

在2.3节和2.4节中，通过假设检验的方法已经分别证明在显著性水平平δ=0.05的情况下，可以认为总体近似服从正态分布，且正态总体的均值μ约为15.1mm。基于类似的方法，不难得到正态总体的标准差σ约等于样本数据的标准差（修正）s=0.4319。基于这样的假设并通过假设检验验证其合理性之后，可以对于产品的生产质量利用数据工序能力指数等指标进行评估。

在工业生产中，为了综合表示工艺水平满足工艺参数规范要求的程度，通常借助于工序能力指数 (Process Capability index, Cp or Cpk) 来描述生产线是否具有较高的工艺水平能否生产出质量好的产品。潜在工序能力指数Cp的定义为：

$$
Cp=\frac{T_U-T_L}{6\sigma}
$$
其中T_U，T_L分别表示工艺参数规范的上限和下限。在本项目的问题背景之下，一般认为滚珠直径在14mm-16mm都可视为合理；但值得注意的是，在此定义中，隐含要求工艺参数分布中心μ与工艺规范要求的中心值T_0=(T_U+T_L)/2相重合。由2.4节的均值检验过程可知，μ约为15.1且上下限14和16的均值15不在可以通过假设检验的区间范围内，因此在此先进行近似处理，假定T_U=16.1，T_L=14.1，则可以计算出此时的潜在工序能力指数Cp=0.7717：

1
2
3
4
5

Tu=16.1;
Tl=14.1;
spec_limits = [Tl, Tu]; 
sigma = std(data(:)); 
cp = (spec_limits(2) - spec_limits(1)) / (6 * sigma);

而事实上，在原设定T_U=16，T_L=14的条件下，由于规范中心T_0=(T_U+T_L)/2与参数分布中心μ不重合，上述的近似处理并不能很准确在的反映其工序能力，此时则需要采用实际工序能力指数Cpk来度量工艺水平的高低：

$$
Cpk=\frac{T_U-T_L}{6\sigma}(1-K)
$$
其中K用于度量工艺参数分布均值μ对规范中心T_0的相对偏离度，即：

$$
K=\frac { {|\mu-T}_0|} { {(T}_U-T_L)/2}
$$

1
2
3
4
5
6

Tu=16;
Tl=14;
spec_limits = [Tl, Tu]; 
T0=(spec_limits(2) + spec_limits(1)) / 2;
k=abs(overall_mean-T0)*2/(spec_limits(2) - spec_limits(1));
cpk=(spec_limits(2) - spec_limits(1)) *(1-k)/ (6 * sigma);

计算得到：相对偏离度K=0.1064，实际工序能力指数Cpk=0.6896。其中相对偏离度K<1，说明均值未偏离到规范范围外，表明工艺加工结果合适，且实际工序能力指数Cpk>0，表明该工序具有一定的生产能力，但并未达到国际上的普遍要求Cpk>1.5，说明生产水平还存在相当大的提升空间。

除此之外，还可以计算单侧规范下的实际工序能力指数C_PU和C_PL:

若工艺参数只有上规范T_U的要求，则实际工序能力指数C_PU定义为：
$$
C_{PU}=\frac{T_U-\mu}{3\sigma}
$$
若工艺参数只有下规范T_L的要求，则实际工序能力指数C_PL定义为：
$$
C_{PL}=\frac { {\mu-T}_L}{3\sigma}
$$

1
2

cpu = (spec_limits(2) - mean(data(:))) / (3 * sigma);
cpl = (mean(data(:)) - spec_limits(1)) / (3 * sigma);

计算得到：实际工序能力指数C_PU=0.6896、C_PL=0.8538，也并未达到国际一般标准。

均值控制图与方差控制图

Shewhart控制图是实施SPC过程中判断生产过程是否处于统计受控状态的基本工具，其中使用最为广泛的为均值控制图和方差（标准差）控制图。通过连续采集工艺参数数据，可以利用Shewhart控制图来定量分析和度量生产线的运行过程处于统计受控状态。

均值控制图

在均值控制图中，包含有三条水平线，分别是：

• **UCL(Upper Control Limit)**：表示上控制限；

• **LCL(Lower Control Limit)**：表示下控制限；

• **CL(Center Line)/Avg(Average)**：表示中心线。

对于各批次的样本数据，用折线连接每批次的均值，从而得到反映不同批次数据均值波动情况的折线图。

对于服从正态分布总体N(μ, σ^2)的工艺参数而言，其取值落在(μ ± 3σ)区间范围内的概率为99.73%，因此可以采用如下的3σ准则来确定均值控制图的中心线以及上下控制限：

$$
UCL=\mu+3\sigma
$$

$$
CL=\mu
$$

$$
LCL=\mu-3\sigma
$$

* 我国标准”GB/T 4091常规控制图(2001版)”规定采用上述法则来计算控制限。

基于以上法则，可绘制均值控制图如下：

1
2
3
4
5
6
7
8
9
10

miu_hat=overall_mean;
sigma_hat=overall_variance;
figure;
plot(means, 'o-');
CL= miu_hat;
UCL=miu_hat+3*sigma_hat;
LCL=miu_hat-3*sigma_hat
yline(CL, 'r-', 'CL');
yline(UCL, 'r--', 'UCL');
yline(LCL, 'r--', 'LCL');

但在实际生产实践中，并不是所有的产品工艺指标都会近似服从正态分布。因此，在实际操作中，均值控制限常用如下公式估算：

$$
UCL=\hat{\mu}+A_s\bullet \hat{s}
$$

$$
CL=\hat{\mu}
$$

$$
LCL=\hat{\mu}-A_s\bullet \hat{s}
$$

其中，若采集工艺参数样本数据组数k=25，各批次数据数量n=5，令x_ij表示第i批次的第j个数据，bar{x_i}表示组内均值；则可用μ表示个各批次所有数据的样本均值，hat{s}表示各个批次数据标准偏差的算数平均值，即：

$$
{\bar{x}}i=\frac{1}{n}\sum{j=1}^{n}x_{ij}
$$

$$
\hat{s}=\frac{1}{k}\sum_{i=1}^{k}{\hat{s}}_i
$$

$$
\hat{\mu}=\frac{1}{k}\sum_{i=1}^{k}{\bar{x}}i=\frac{1}{kn}\sum{i=1}^{k}\sum_{j=1}^{n}x_{ij}
$$

$$
{\hat{s}}i=\sqrt{\frac{1}{n-1}\sum{j=1}^{n}{ {(x}_{ij}-{\bar{x} }_i)}^2}
$$

又查表[^2]可得：当每批次样本数据数n=5时，有A_s=1.427。

于是绘制出实际均值控制图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

figure;
plot(means, 'o-');
xi=mean(data, 2);
for i=1:num_groups
    sum=0;
    for j=1:samples_per_group
        sum=sum+((data(i,j)-xi(i))^2);   
    end
    si_hat(i)=sqrt(sum/(num_groups-1));
end
s_hat=mean(si_hat);
As=1.427;
CL= miu_hat;
UCL=miu_hat+s_hat*As;
LCL=miu_hat-s_hat*As;
yline(CL, 'r-', 'CL');
yline(UCL, 'r--', 'UCL');
yline(LCL, 'r--', 'LCL');

方差控制图

方差控制图的结构与均值控制图非常类似，也是由中心线以及上下控制限构成。只是图中的数据点描述的每批次数据的标准偏差，因此可用于定量判断不同批次数据的标准偏差(数据的波动性)在变化中是否存在”异常因素”。

类似于均值控制图，在实际操作中，常用如下公式估算其中心线以及上下控制限：

$$
UCL=B_U\bullet\ \hat{s}
$$

$$
CL=\hat{s}
$$

$$
LCL=B_L\bullet\hat{s}
$$

其中B_U、B_L为依赖于每批次样本数据数n的常数参数，查表[^2]可得：当每批次样本数据数n=5时，有B_U=2.089、B_L=0。

据此可绘制出对应的方差控制图：

1
2
3
4
5
6
7
8
9
10
11

Bu=2.089;
Bl=0;
figure;
plot(variances, 'o-');
hold on;
UCL=(Bu*s_hat);
CL=(s_hat);
LCL=(Bl*s_hat);
yline(CL, 'r-', 'CL');
yline(UCL, 'r--', 'UCL');
yline(LCL, 'r--', 'LCL');

产品质量分析结论

为根据Shewhart控制图判断产品生产过程是否受控，可对于均值控制图与方差控制图分别采用如下八条常见规则（规则均不能触碰，否则视为不受控），以识别产品生产过程是否仅受到随机因素影响：

• 规则 1:控制图上有一个点(对应某个批次数据)位于控制限以外；

• 规则 2:连续9个点落在中心线同一侧；

• 规则 3:连续6个点递增或者递减；

• 规则 4:连续14个点交替上下；

• 规则 5:连续3个点中有2个点落在中心线同侧的B区以外；

• 规则 6:连续5个点中有4个点落在中心线同侧的C区以外；

• 规则 7:连续15个点落在中心线两侧的C区；

• 规则 8:连续8个点落在中心线两侧且无一点在C区以内。

其中，A、B、C分区如下图^^[@2]^^所示，C区为以CL控制限为对称轴的中心区域，B、A两区向两侧延伸至上下控制限UCL与LCL。

实际上，Matlab软件中对于Shewhart控制图以及SPC统计过程控制方法有一套完整封装的库函数controlchart()，调用结果如下所示：

1
2

load parts
[st,plotdata] = controlchart(data,'charttype',{'xbar' 's'});

其中第一张图为均值控制图，第二张图为标准差控制图。

通过观察图像，基于八大规则进行判断并通过查看返回对象plotdata的ooc属性（Logical that is true for points that are out of control）可知，该产品生产过程确实处于统计受控状态。除此之外，样本均值也在15.1mm左右，符合对于滚珠直径的一般行业要求，工艺水平良好；但实际工序能力指数Cpk仅有0.6896，说明工艺水平还有上升空间。

参考文献

[^1]: 茆诗松,程依明,濮晓龙编著. 概率论与数理统计教程[M]. 高等教育出版社, 2019.
[^2]: 贾新章 .. [等] 编著. 统计过程控制理论与实践[M]. 电子工业出版社, 2017.

摘要

本报告主要探讨了救灾机器人在人机交互和远程控制平台设计中的距离特性问题。通过Unity软件搭建模拟实验平台，并收集操作人员在操作机器人”抓取”持续运动的目标救助人员时的相关数据，基于Matlab软件进行数据分析，挖掘用户潜在的操作习惯与背后的操作逻辑规律。研究表明，在机器人与目标救援人员为相遇（拦截）关系的前提下，通过摄像头远程返回影像做出抓取判断时的决策距离与待救援人员运动的速度成正相关，而与机器人移动的速度成负相关。这些发现对未来进一步改进远程救援控制平台的设计及机器人相关物理参数的优化具有重要意义。

关键词: 救灾机器人、人机交互、距离特性、Unity、Matlab

Introduction

救灾机器人是在安全生产和防灾减灾救灾过程中，执行监测预警、搜索救援、通信指挥、后勤保障、生产作业等任务，能够实现半自主或全自主控制，部分替代或完全替代人类工作的智能机器系统的总称。救灾机器人具有感知、决策、执行等特征，可提升复杂危险场景中生产和救援的效率与安全性。地震、火灾、核泄漏等事故发生时，由于事故现场环境复杂、风险因素较多，同时可能伴有次生灾害，因此现在越来越多的事故现场救援初期采用救灾机器人进行现场救援。救灾机器人的发展与应用，代表了应急管理装备现代化发展趋势，是衡量我国应急管理体系与能力现代化的重要标志。

常见的火灾救灾机器人（如下图）主要由以下几个基本部分组成：

• 行走机构：用于在复杂的地表环境下行走。

• 影音采集机构（如摄像头等）：用于采集复杂环境下的环境信息。

• 机械臂：用于远程操控执行部分操作。

在救灾机器人的实际使用过程中，一般通过无线通信的方式将救灾现场的影音信息远程传送给操作人员，并由操作人员对于机器人进行一系列操作，包括控制机器人的行走路径、通过机器人的机械臂进行障碍物移除、爆炸物拆除等操作，这些操作也往往通过远程控制平台实现。因此，设计一个能与机器人自身操作特性（尺寸等参数）良好契合且操作效率与精准度较高、简洁易用的远程救援控制平台是提高救援成功率的关键。

在远程救援控制平台的设计过程中必不可少地需要关注到人机交互的相关问题。一个值得注意的问题是，操作人员对于救灾机器人的物理参数可能相对了解较少，特别是在只能借助于机载摄像头对周围环境进行观察的情况下，无法通过摄像头远程返回的画面精准判断机器人与目标救助人员（多为行动不便）之间的距离，从而可能会因为二者的交互失败导致目标救助人员无法通过搭乘救灾机器人实现逃生，使得救援成功率不理想，甚至可能会由于机械臂的误操作等对目标救助人员造成二次伤害，这是我们所不希望看到的。因此，希望通过收集操作人员（用户）在模拟实验平台中操作机器人”抓取”持续运动的目标救助人员时的相关数据，分析用户的操作习惯，从而更好地指导远程救援控制平台的设计以及机器人相关物理参数与摄像头摆放位置等的改进。

Literature Review

▼ 文献1[^1] : The different characteristics of human performance in selecting receding and approaching targets by rotating the head in a 3D virtual environment

综述: 初始距离、目标移动速度和目标容差对于操作的准确性影响较大。初始距离会影响抓取操作的时间特性，在远离运动中，需要以高于目标速度追击目标，而靠近运动中则需要拦截目标。目标移动速度增大会增加抓取难度，特别是在远离运动中，影响更为显著。目标容差主要影响调整阶段，影响抓取精度，但不影响加速和减速阶段。

▼ 文献2[^2]: Beyond Fitts’s Law: A Three-Phase Model Predicts Movement Time to Position an Object in an Immersive 3D Virtual Environment

综述: 理解距离特性对三维场景下的准确抓取来说至关重要。目标定位任务在三维虚拟环境中的特点明显不同于二维界面。例如，三维空间中的目标操作涉及大范围的手臂移动和虚拟手或射线投射技术。研究指出，人类的目标导向手臂运动包括快速的弹道阶段和慢速的修正阶段，这两个阶段在不同的因素影响下表现各异。此外，目标大小、运动幅度和目标容差是影响定位时间的主要因素，这些因素在三维环境中与传统的二维环境有所不同。

▼ 文献3[^3]: Capture of moving targets: amodification of Fitts’ Law

综述: 该文章主要描述了一个根据Jagacinski等人的实验数据开发的数学模型，用于描述移动目标的捕获时间。该模型在位置和速度控制系统下都经过了测试，并且与实验数据拟合良好。在移动目标下，该模型对Fitts定律的主要修改在于稳态位置误差，从而减小了有效目标宽度。在静止目标情况下，该模型退化为经典的Fitts定律。该模型预测了一个临界速度，超过这个速度目标将无法被捕获，这与Jagacinski等人的实验数据相符，可用于理解救灾机器人在不同速度下捕获目标的效率和限制。

▼ 文献4[^4] : 面向人机交互的机器人信息融合系统的研究与实现

综述: 本篇文章主要探讨了在人机交互中，利用多传感器信息融合技术提升机器人对人体目标跟随的效率和精度。作者提出了一个面向人机交互的机器人信息融合系统，包括人体感知、视觉跟踪和运动跟随模块。通过运用帧间差分法和骨架验证识别人体目标，利用小波变换融合深度图像和反向投影图提高视觉跟踪精度，并采用位姿信息融合方法实现运动跟随。这些技术和系统设计有助于提升机器人在火灾场景下抓取目标救助对象的距离检测的精准性。

▼ 文献5[^5] : 三维虚拟空间中物体移动操作的交互模型

综述: 这项研究通过三个实验系统探讨了影响3D空间物体移动效率的因素，并建立了相应的数学模型。研究发现，除了传统的移动距离和目标大小外，被移动物体的大小和所处深度也影响移动效率。实验结果表明，移动物体的大小影响移动过程中的加速阶段，而移动物体所处的深度则影响整体移动时间。通过以视角为单位的修正模型，研究者成功地拟合了实验数据，提高了移动操作效率的预测准确性。这一研究成果为虚拟3D空间中的人机交互设计提供了有益的参考，可为设计更有效的救灾机器人操作策略提供理论支持。

▼ 文献6[^6] : 虚拟运动目标人机交互方法设计与仿真

综述: 这项研究提出了一种基于多体感融合的虚拟运动目标人机交互方法，以解决当前虚拟手型逼真度偏低的问题。利用Kinect采集深度图像和彩色图像，结合颜色直方图匹配结果，实现了对虚拟运动目标的准确识别和跟踪。通过提取目标结构信息并融合全部体感特征，构建了笛卡尔空间映射关系，以实现人机交互。仿真结果显示，该方法不仅能够获取高逼真度的虚拟手型，还能够准确跟踪和识别目标，为解决商场火灾场景下救灾机器人抓取目标救助对象的距离特性提供了实用性解决方案，使虚拟实验平台上的交互操作在现实中成为可能。

▼ 文献7[^7] : 救灾机器人远程操作控制台设计

综述: 本篇文章强调了在各种灾难中，特别是火灾等复杂环境下，使用消防机器人进行救援的必要性，从消防救援的角度出发，针对地震、火灾、核泄漏等灾害提出了机器人功能需求，并结合人因工程学等相关学科知识，从宏观层面探讨了远程操作平台的构建方法，并给出了一些关键的参考数值，为实验平台的搭建提供了指导性的重要参考。

▼ 文献8[^8] : 可变形履带机器人数字孪生测试平台研究

综述: 作者利用Unity引擎开展了关于多地形多运动模式矿井救灾机器人的研究，围绕虚拟空间生成崎岖巷道的数字孪生环境展开，建立了数字化描述模型，并实现了可变形履带机器人的现实层面与抽象层面的复制，构建了物理级和系统级的数字孪生样机，以及信息级的数字孪生平台。这项研究的方法和成果为类似商场火灾场景下的救灾机器人开发提供了借鉴，特别是在抓取目标救助对象的距离特性研究方面，为机器人的设计与测试提供了新思路和技术支持。

▼ 文献9[^9] : 一种基于三维建图和虚拟现实的人机交互系统

综述: 该研究提出了基于三维建图和虚拟现实技术的人机交互系统，旨在提高救援机器人在商场火灾场景下的应用效率。操作人员则可通过虚拟现实系统的交互设备生成控制指令，实现对机器人的运动控制。这一系统不仅能够将机器人环境实时可视化，提供操作人员极强的沉浸感，还为人与机器人的自然交互提供了新的思路，对于促进人机交互技术的发展具有重要意义，也从技术层面为救援机器人在路径规划导航与精准定位抓取等方面提供有力支持。

▼ 文献10[^10] : 多模态交互中的目标选择技术

综述: 多模态交互技术利用各种传感器捕获的信息，预测人的交互意图，提升机器对人行为的理解能力，尤其适用于目标选择任务。在人机交互系统中，目标选择任务是一项基础任务，已有多个行为模型针对多模态交互进行了描述，这些理论对于开发多模态交互技术具有指导意义，可以有效推动人机交互向更自然的方向发展，也为远程操作平台在机器人与多个目标救助人员的交互逻辑设计方面提供参考。

Method and Results

在一系列对于机器人与操作平台基本需求分析的基础上，我们基于Unity软件搭建了救灾机器人远程救援模拟实验平台，并希望通过模拟实验来帮助实际平台设计进行进一步改进。落实到该实验平台，本次研究的主题可以这么描述：通过收集用户操作机器人对虚拟人实现救援过程的数据，具体而言即”救援”这一行动（平台中的交互方式表现为机器人会”抓取”待救援人员并”牵引”其共同移动到终点）中的”抓取”行为（实验中简化为用户判断并发出抓取指令与完成抓取动作过程中无延迟）发生前的瞬间机器人与待救援人员之间的距离以及两者各自的运动速度，对其进行数据分析，从而寻找彼此之间的关系。实际上，用户（即操作人员）在无任何提示的情况下，应根据摄像头回传画面中出现的待救援人员的图像来判断两者之间的距离，当用户认为距离合适时便会做出判断、发出”抓取”指令以施行救援。但这样的主观判断往往具有不确定性，很容易造成误判从而带来不必要的损失甚至是二次伤害。因此，我们希望通过模拟实验的数据分析，初步得到机器人和待救援人员的移动速度与合适的实际抓取距离之间的关系，尽可能地探索用户主观判断抓取时机的规律，从而可以在检测两者数据的情况下，推测两者与合适的实际抓取距离之间的关系，进而可以提前在用户操作平台界面以UI形式给出提示，实现更精准更快速的救援，提高救援效率；同时这样的结果也可以反馈到摄像头安装位置的确定以及机械臂长度等等物理参数的确定过程，基于人因与工效学实验的结果进一步优化整体的结构设计，使整体更易上手、提高易用性。

在Unity远程救援模拟实验平台中，事先编写脚本记录所需要的实验数据，主要包括”抓取”动作发生时（按下鼠标左键即执行抓取，最大抓取范围设置为5单位）机器人与待救援人员之间的距离以及两者各自的移动速度，并编写控制与交互脚本，保证各项功能正常运行。考虑到实际应用场景，整体环境设置为商场场景，共设置3位NPC（动画与外形素材来源于蒯曙光老师的素材库[^11] ），各自具有不同的移动速度与行进路线；场地内模拟火灾场景，随时间推移火势会不断蔓延（烟雾扩散），在烟雾逼近时NPC会主动向最近的出口奔跑逃生，但行动不便的顾客移动速度较慢，需要机器人对其实施救援。用户（操作者）需要操作机器人，从入口出发进入火灾现场，通过”抓取”操作实施救援，最终将所有的顾客NPC全部救出至安全出口。值得注意的是，本实验仅考虑文献1[^1]中的简化情形，即只考虑机器人从正面”拦截”目标；这样的假设相对是合理的，因为机器人同样是从安全出口进入商场，寻找被困人员并将其带至安全出口，基本不存在从后方”追击”被困人员的情况，且实际实验过程中在具有多视角地图的情况下（实际操作时也会将商场平面图提前导入机器人与操作平台）也没有实验者采取”绕远路”的方式实行救援。

邀请到同组的5位同学作为实验者，每个人完成10次救援，共得到50组数据，并利用Matlab软件对于导出的数据集进行数据分析。原始数据集、代码与Unity实验环境均已上传至Github（链接：https://github.com/Asgard-Tim/ergonomic），在此仅对于数据分析过程与结果进行必要性的说明：

首先，对于抓取时刻的数据参数进行研究，明确自变量：机器人的移动速度robospeed、待救援人员的移动速度humanspeed；因变量：两者间相距距离distance。对于两个不同的自变量，分别以其为横轴，两者相距距离为纵轴，绘制散点图（下左图，颜色反映另一未在坐标轴上的变量值）；

可以看到， 由于顾客NPC在行走与奔跑逃生时都有各自的固定设定速度，右侧以humanspeed为横坐标的散点图的数值点集中分布在0*.5,* 0*.8, 2.0, 2.8四处。于是，在这样四个特定的humanspeed聚集点上，分别对各点对应的决策距离distance取均值并绘制直方图观察其关于NPC移动速度humanspeed的变化趋势（上右图）：随着humanspeed的增加，执行”抓取”操作的决策距离distance*也呈递增趋势。

虽然机器人的速度在实验平台中并没有以固定值的方式明确，但是在实际操作运行中机器人的移动速度robospeed仍然在2*.2937与2.*5291两发生了大批量的聚集现象。这里的探讨分两方面进行：

首先还是将聚集点用均值代替以观察总体上决策距离distance随机器人移动速度robospeed的变化趋势（下左图）；

尽管递减趋势较为明显，即机器人移动速度robospeed应与决策距离distance呈负相关关系，但散点图的线性度并不好，可能是由于存在相对较大的实验误差，或是本身就不成线性关系；较为有限的样本量也导致暂时找不到较为合适的初等函数对两者关系进行拟合。

另一方面，还可以对上述的数据处理过程做进一步拓展，即对于聚集点2*.2937与2.5291两处的数据可以从NPC移动速度humanspeed与决策距离distance变化关系的角度再次观测（如上右图），可以看到在这两个聚集点处NPC移动速度humanspeed与决策距离distance*仍然成正相关关系。

从总体而言，决策距离distance的均值为2*.8724，NPC移动速度humanspeed的均值为1.5660，机器人移动速度robospeed的均值为2.*3549。这为后续对于三者特别是决策距离的平均水平的宏观把握提供了一定的参考价值。

Discussion and Conclusion

遗憾的是，由于各方面条件限制，实验条件与样本数量有限，从50个小样本数据中很难得到更加一般化的公式层面的结果来反映用户的决策距离distance与两者移动速度之间的定量关系，只是从定性角度进行分析。事实上，在文献7[^7]中有给出一些相应的数值参考， 但并未在我们的模型上取得良好的效果；而文献2[^2] 、文献3[^3]虽然给出了基于Fitts′ Law的公式化的结论，但也未在我们的实验数据集上得到良好的验证。但总体而言，我们的实验数据得到的初步统计分析的结果所反映出来的变化趋势与文献中所给出的函数的趋势走向是大致一致的，即：用户根据摄像头进行执行”抓取”操作判断的决策距离distance与NPC移动速度humanspeed成正相关，与机器人移动速度robospeed成负相关，这也验证了我们研究的有效性与可行性。希望能在未来能够进一步完善整个模拟操控平台、收集到更多的数据以完善统计结论，从而简化整体的交互设计，使最终实装的远程救援控制平台更加人性化、便捷、易上手，提高救援成功率，让更多的人享受科学技术带来的福祉。

参考文献

[^1]: DENG Chenglong, GENG Peng, KUAI Shuguang. (2023). The different characteristics of human performance in selecting receding and approaching targets by rotating the head in a 3D virtual environment. Acta Psychologica Sinica, 55(1), 9-21.
[^2]: Deng, C.-L., Geng, P., Hu, Y.-F., & Kuai, S.-G. (2019). Beyond Fitts’ s Law: A Three-Phase Model Predicts Movement Time to Position an Object in an Immer- sive 3D Virtual Environment. Human Factors, 61(6), 879-894.
[^3]: ERROL R. HOFFMANN (1991) Capture of moving targets: a modification of Fitts’ Law, Ergonomics, 34:2, 211-220.
[^4]: 刘素成. 面向人机交互的机器人信息融合系统的研究与实现[D].电子科技大学,2018.
[^5]:邓成龙,胡逸,耿鹏,等. 三维虚拟空间中物体移动操作的交互模型[C]//中国心理学会.第二十届全国心理学学术会议–心理学与国民心理健康摘要集.[出版者不详],2017:2.
[^6]:龙年, 刘智惠. 虚拟运动目标人机交互方法设计与仿真[J]. 计算机仿真,2022, 39(06):201-205.
[^7]: 于彦凤,刘力源,楚炎.救灾机器人远程操作控制台设计[J].大众标准化,2021(18):220-222.
[^8]: 魏桢. 可变形履带机器人数字孪生测试平台研究[D]. 中国矿业大学,2022.
[^9]: 张辉,王盼,肖军浩,等.一种基于三维建图和虚拟现实的人机交互系统[J].控制与决策,2018,33(11):1975-1982.
[^10]: 周小舟, 宗承龙, 郭一冰, 等. 多模态交互中的目标选择技术[J]. 包装工程,2022,43(04):36-44.
[^11]: Zhou, C., Han, M., Liang, Q., Hu, Y.-F., & Kuai, S.-G. (2019). A social interaction field model accurately identifies static and dynamic social groupings. Nature Hu- man Behaviour, 3(8), 847–855.